Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

494 Chapter 11 Intersection in 3D
P
d
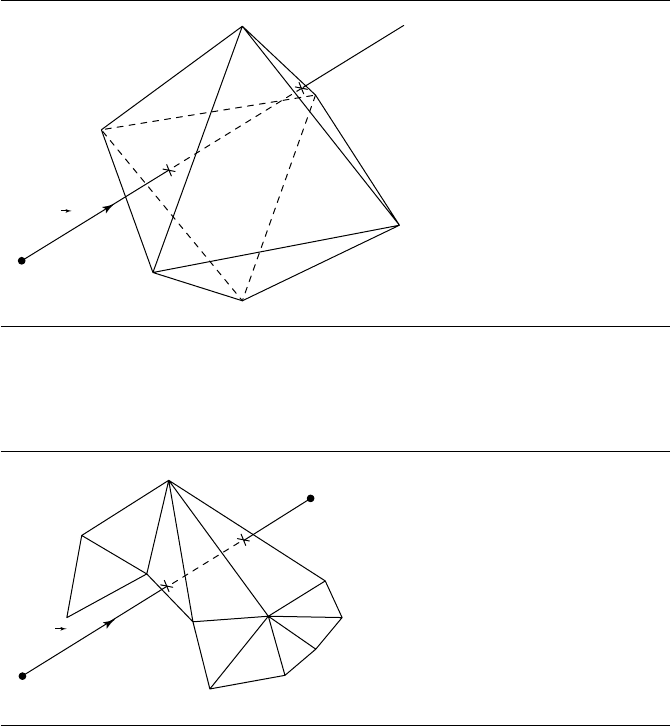
Figure 11.5 Intersection of a ray and a polyhedron (octahedron).
P
1
P
0
d
Figure 11.6 Intersection of a line segment and a polygonal (triangle) mesh.
As a polyhedron or polygonal mesh is simply a collection of polygons obeying
specific rules regarding shared edges and vertices, the simplest approach is to test each
face in succession for intersection (see Section 11.1.3). However, for polyhedra or
polygonal meshes with a significant number of faces, this naive approach is extremely
inefficient because it spends a lot of time computing intersections with faces that are
nowhere near the linear component. In such cases, the application should employ a
spatial-partitioning scheme, such as an octree or binary space-partitioning tree (see
Foley et al. 1996 or Chapter 13). The cost of constructing such a spatial-partitioning
scheme will be well worth incurring if there are a large number of faces, particularly if

11.2 Linear Components and Polyhedra 495
the polyhedron or polygonal mesh is to be intersected many times (as in ray tracing,
for example).
Eric Haines (1991) describes an algorithm, based on the ideas of Roth (1981)
and Kay and Kajiya (1986), for convex polyhedra that is significantly faster than the
naive approach, an advantage due to the fact that he intersects the linear component
with the planes containing each face (which is relatively cheap), rather than with the
polygonal faces themselves (which can be quite expensive). The linear component is
L(t) = P + t
ˆ
d
and the planes of the faces are defined as
ax + by + cz + d = 0
Given these definitions, the distance from the linear component’s origin P and its
intersection with the plane P of a face of the polyhedron is
t
0
=
−(n · P + d)
n ·
ˆ
d
(11.6)
where n = [
abc
]is the plane normal of P. If the denominator of Equation 11.6
is (near) zero, then the linear component is parallel to the plane; in this case the sign
of the numerator indicates on which side of the plane the linear component’s origin
lies. Otherwise, the sign of the denominator indicates whether the linear component
has intersected the front of the plane or the back: if it is positive, then the plane
is intersected from the back (in terms of increasing t), and vice versa if the sign is
negative.
The idea behind Haines’s algorithm is this: the volume defined by a polyhedron
can be understood to be the logical intersection of the half-spaces defined by the
planes in which its faces lie. If we consider a linear component, its intersection with
a polyhedron consists of a portion of it that is entirely contained within the half-
spaces. The intersection of a linear component with each face’s plane partitions the
linear component into two regions—one that is “outside” the half-space defined by
that plane and one that is “inside” the half-space. From these facts we can conclude
that the portion of the linear component that intersects the entire polyhedron is the
logical intersection of the portions (of the linear component) that are within the half-
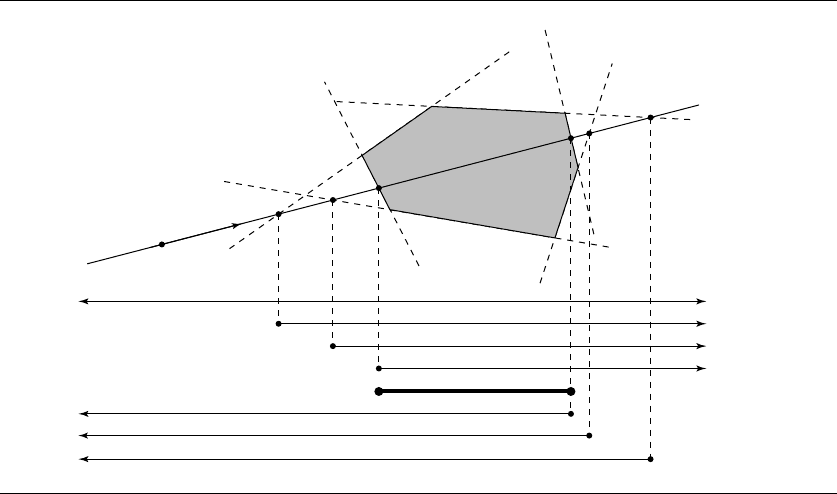
space defined by each face’s plane. This is illustrated (in 2D, for clarity) in Figure 11.7.
Note that we’ve not listed the half-lines in order of increasing edge index, but
rather in order of increasing intersection distance; this should make more evident
the nature of their logical intersection. Any line that intersects a polyhedron will first
intersect one or more “front faces” (if you consider the line “starting” at t =−∞)
and then some number of “back faces.” The logical intersection is bounded by the
last (farthest) front face and the first (nearest) back face.
496 Chapter 11 Intersection in 3D
0
2
3
4
5
Line
P
Face 4
Face 0
Face 5
Logical intersection
Face 2
Face 1
Face 3
1
d
ˆ
Figure 11.7 The logical intersection of half-lines defines the intersection of a line with a polyhedron.
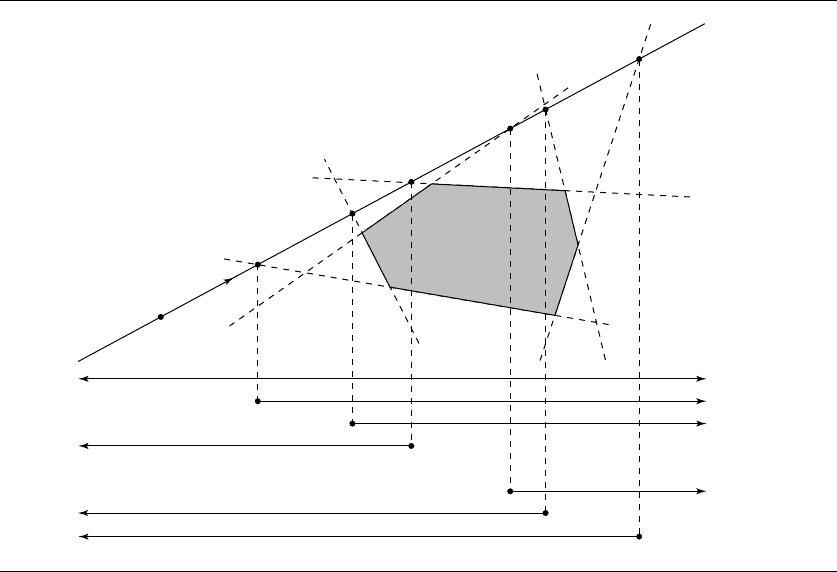
Note that if the line does not intersect the polyhedron, as in Figure 11.8, then the
line intersects a front face’s plane after it has hit a back face’s plane, and so the logical
intersection doesn’t exist.
This analysis leads to a simple algorithm. The only additional thing to note is
that if we find a face-plane that is parallel to the line, and find that the line is to the
outside of that plane, we can exit early from the algorithm, as no intersection with
the polyhedron is possible in this case.
The pseudocode is as follows:
boolean LinePolyhedronIntersection(
Line line,
Polyhedron phd,
float& tNear,
float& tFar)
{
tNear = -MAXFLOAT;
tFar = MAXFLOAT;
foreach face F in polyhedron {
normal = { F.a, F.b, F.c };
11.2 Linear Components and Polyhedra 497
denominator = Dot(normal, line.direction);
numerator = Dot(normal, line.origin) + F.d;
if (denominator < epsilon) {
//
// Face F is parallel to the line. Check
// if line is outside the half-space
// defined by the plane
//
if (numerator > 0) {
//
// Line is outside face and therefore
// outside the polyhedron.
//
return false;
}
} else {
//
// Check if face is front- or back-facing
//
t = -numerator / denominator;
if (denominator > 0) {
// Back-facing plane. Update tFar.
if (t < tFar) {
tFar = t;
}
} else {
// Front-facing plane. Update tNear.
if (t > tNear) {
tNear = t;
}
}
//
// Check for invalid logical intersection
// of half-lines.
//
if (tNear > tFar) {
return false;
}
}
}
return true;
}
498 Chapter 11 Intersection in 3D
0
2
3
4
5
Line
Face 0
Face 5
Face 3
Logical intersection = ?
Face 4
Face 2
Face 1
1
P
d
ˆ
Figure 11.8 The logical intersection of half-lines fails to exist if the line does not intersect the poly-
hedron.
Ray or Segment and Polyhedron
In the case of a ray, it may be that the ray’s origin is within the polyhedron itself. The
previous algorithm for lines can be modified to handle rays by checking the value of
t
near
to see if it is less than 0, in which case the ray originates inside the half-space
defined by the plane in question. If this is the case, then check if t
far
< ∞: if it is, then
t
far
is the first valid intersection.
In the case of a line segment, we must check the computed values of t to see if
they are in the range 0 ≤t ≤ 1.
11.3 Linear Components and Quadric Surfaces
Quadric surfaces include ellipsoids, cylinders, cones, hyperboloids, and paraboloids
(see Section 9.4). A general method for intersecting linear components with quadric

11.3 Linear Components and Quadric Surfaces 499
surfaces is covered in the next section; however, this method does not take advantage
of the geometry of any particular quadric. Algorithms specific to particular quadrics
are typically more efficient, and we cover a number of them in this section.
11.3.1 General Quadric Surfaces
The general implicit form of the equation for a quadric surface is
q(x, y, z) = ax
2
+ 2bxy + 2cxz + 2dx + ey
2
+ 2fyz +2gy +hz
2
+ 2iz + j =0
(11.7)
This can be expressed in matrix notation as
[
xyz1
]
abcd
befg
cf h i
dg i j
x
y
z
1
= 0 (11.8)
If we let X =[
xyz1
], we can more compactly represent a quadric as
XQX
T
= 0 (11.9)
The intersection of a line L(t) = P + t
d with a quadric can be computed by
substituting the line equation directly into Equation 11.9:
q(x, y, z) = XQX
T
=
[
P + t
d
]
Q
[
P + t
d
]
T
= (
dQ
d
T
)t
2
+ (
dQP
T
+ P Q
d
T
)t + P QP
T
= 0
This is a quadratic equation of the form
at
2
+ bt + c = 0
which can be solved in the usual fashion:
t =
b ±
√
b
2
− 4ac
2a
If there are two distinct real (nonimaginary) roots of this, then the quadric is inter-
sected twice. If there are two real roots of the same value, then the line is touching,
but not penetrating, the quadric. If the roots are imaginary (when the discriminant
b
2
− 4ac < 0), then the line does not intersect the surface.
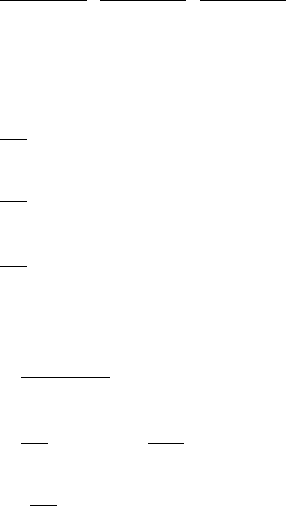
500 Chapter 11 Intersection in 3D
The normal for an implicitly defined surface q(x, y, z) = 0atapointS on the
surface is the gradient of q:
n
S
=∇q(S)
In terms of Equation 11.9, we have
n = 2
1000
0100
0010
0000
QS
T
This last step may require some explanation: in general
∇f(x, y, z) =
∂f (x , y, z)
∂x
,
∂f (x , y, z)
∂y
,
∂f (x , y, z)
∂z
That is, we simply compute the partial derivatives with respect to the basis vectors of
the quadric’s frame. Again referring back to the compact matrix notation, we have
∂X
∂x
=
[
1000
]
∂X
∂y
=
[
0100
]
∂X
∂z
=
[
0010
]
For example,
n
x
=
∂f(x, y, z)
∂x
=
∂X
∂x
QX
T
+ XQ
∂X
T
∂x
= 2
∂X
∂x
QX
T
= 2
[
1000
]
QX
T
The pseudocode is
int LineQuadricIntersection(Matrix4x4 Q, Line3D l, float t[2])
{
float a, b, c;
Matrix dTrans = transpose(l.d);
11.3 Linear Components and Quadric Surfaces 501
// * denotes matrix multiplication
a = dTrans*Q*l.d;
b = dTrans*Q*l.p+transpose(l.p)*Q*l.d;
c = transpose(l.p)*Q*l.p;
float discrm=b*b-4*a*c;
if (discrm < 0) {
return 0;
}
if (discrm == 0) {
t[0]=b/(2*a);
return 1;
} else {
t[0] = (-b + sqrt(discrm)) / (2 * a);
t[1] = (-b - sqrt(discrm)) / (2 * a);
}
return 2;
}
11.3.2 Linear Components and a Sphere
For the purposes of this section, a sphere is represented by a center C and radius r,
so that the implicit equation for the sphere is
f(X)=X −C
2
= r
2
(11.10)
The intersection of a linear component (defined by an origin P and direction
vector
ˆ
d) and a sphere can be computed by substituting the equation for a linear
component (Equation 11.2) into Equation 11.10:
X − C
2
= r
2
P + t
ˆ
d − C
2
= r
2
(P − C) + t
ˆ
d
2
= r
2
(t
ˆ
d + (P − C)) · (t
ˆ
d + (P − C)) − r
2
= 0
t
2
(
ˆ
d ·
ˆ
d) +2t(
ˆ
d · (P − C)) + (P −C) · (P −C) − r
2
= 0
t
2
+ 2t(
ˆ
d · (P − C)) + (P −C) · (P −C) − r
2
= 0

502 Chapter 11 Intersection in 3D
This second-order equation is of the form
at
2
+ 2bt +c = 0
and can be solved directly using the quadratic formula:
1
t =
−(
ˆ
d · (P − C)) ±
(
ˆ
d · (P − C))
2
− 4((P −C) · (P −C) − r
2
)
2
(11.11)
There are three possible conditions for line/sphere intersection, each of which can
be identified by the value of the discriminant (
ˆ
d ·(P −C))
2
−4(P −C) ·(P −C) −
r
2
) in Equation 11.11:
i. No intersections: This condition exists if the discriminant is negative, in which
case the roots are imaginary.
ii. One intersection: This happens if the line is tangent to the sphere; in this case the
discriminant is equal to zero.
iii. Two intersections: This happens if the discriminant is greater than zero.
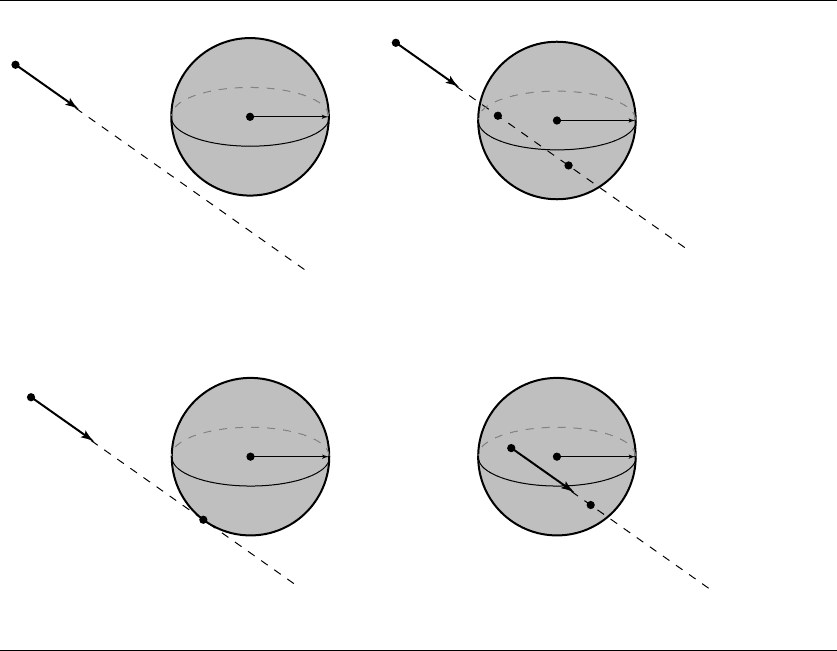
Figure 11.9 shows these three possible configurations, plus the situation in which the
linear component is a ray and has its origin inside the sphere; in the latter case, there
are two intersections, mathematically speaking, but only one of them is within the
bounds of the ray.
The pseudocode is
int LineSphereIntersection(Sphere sphere, Line3d line, float t[2])
{
float a, b, c, discrm;
Vector3D pMinusC = l.origin - sphere.center;
a = Dot(line.direction, line.direction);
b=2*Dot(l.direction, pMinusC);
c = Dot(pMinusC, pMinusC) - sphere.radius * sphere.radius;
discrm=b*b-4*a*c;
if (discrm > 0) {
t[0] = (-b + sqrt(discrm)) / (2 * a);
t[1] = (-b - sqrt(discrm)) / (2 * a);
return 2;
} else if (discrm == 0) {
// The line is tangent to the sphere
1. Recall that a quadratic equation of the form ax
2
+ bx + c = 0 has the two solutions x =
−b±
√
b
2
−4ac
2a
.
11.3 Linear Components and Quadric Surfaces 503
C
C
Q
0
= Q
1
P
C
Q
0
Q
1
P
C
No intersections Two intersections
One intersection
d
ˆ
d
ˆ
d
ˆ
d
ˆ
Q
0
r
r
r
r
P
P
Figure 11.9 Possible ray-sphere intersections.
t[0]=-b/(2*a);
return 1;
} else {
return 0;
}
}
Ray or Line Segment and Sphere
In the case of a ray, the parametric value or values of the intersection (if the discrim-
inant is nonnegative) must be checked for nonnegativity. An inexpensive test for the
