Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

534 Chapter 11 Intersection in 3D

If our planes instead are represented explicitly

: a

x +b

y +c

z + d

= 0

: a

x +b

y +c

z + d

= 0

: a

x +b

y +c

z + d

= 0

then we can view the problem as solving three simultaneous linear equations. A

technique such as Gaussian elimination or Cramer’s rule (see Section 2.7.4) can be

invoked to solve this. Bowyer and Woodwark (1983) condense this as follows: let

BC = b

− b

AC =a

− a

AB = a

− a

DC = d

− d

DB = d

− d

AD = a

− a

invDet =

BC − b

AC −c

X = (b

DC − d

BC − c

DB) ∗ invDet

Y = (d

AC −a

DC − c

AD) ∗ invDet

Z = (b

AD − a

DB − c

AB) ∗ invDet

11.5.3 Triangle and Plane

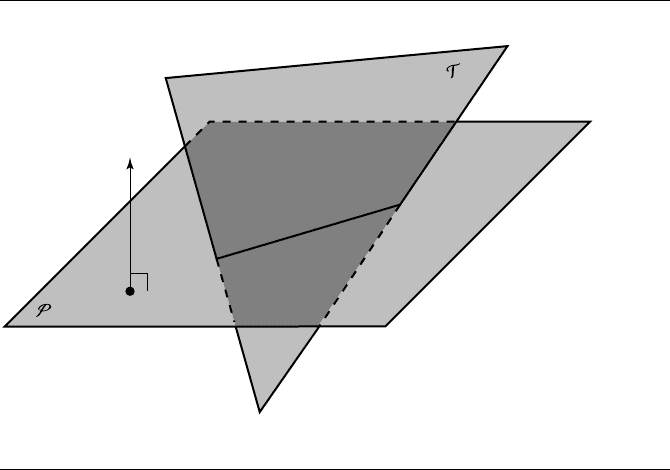
Suppose we have a plane P deﬁned by a point P and normal ˆn, and a triangle T

deﬁned by its three vertices Q

, Q

, and Q

, as shown in Figure 11.25. If the plane

and triangle intersect, then one triangle vertex will be on the opposite side of the plane

than the other two. If we compute the signed distance between each of Q

, Q

, and

and the plane P (see Section10.3.1) and compare their signs, we can immediately

determine if an intersection exists. Without loss of generality, assume that Q

on the side of P opposite Q

and Q

. Then, the two edges Q

and Q

must

intersect P at some points I

and I

, respectively. The line segment I

is then the

intersection of P and T (see Section 11.1.1).

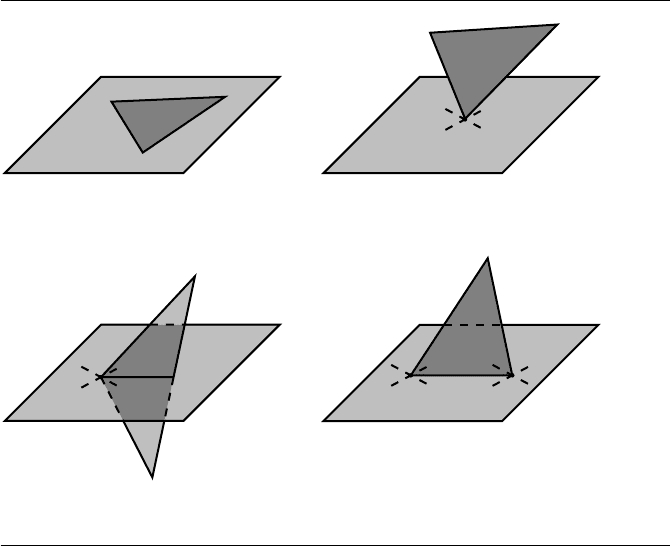
There are a number of “degenerate” cases that may arise, as shown in Figure 11.26.

All of these involve one or more of the triangle’s vertices being exactly on (or within

1 of) the plane. In Figure 11.26(a), P and T are coplanar, and as such should

probably not be considered an intersection, although the context of the application

11.5 Planar Components 535

Figure 11.25 Plane-triangle intersection.

may have to deal with this situation speciﬁcally. The cases in Figures 11.26(b) and

11.26(c) can be handled in the same way, by considering that Q

coinciding with the

plane not be involved with any intersection. The case in Figure 11.26(d) is somewhat

more interesting, as the “intersection” consists of a deﬁnite line segment, just as

in a “normal” intersection; how this is handled depends on the semantics of the

application.

The pseudocode is

bool IntersectionOfTriangleAndPlane(Plane3D p1,Triangle3D tri, p2,

Intersection isect)

{

float dot1, dot2, dot3;

dot1 = Dot(p1.normal, tri.p1 - p1.pointOnPlane);

dot2 = Dot(p1.normal, tri.p2 - p1.pointOnPlane);

dot3 = Dot(p1.normal, tri.p3 - p1.pointOnPlane);

if (fabs(dot1) <= EPSILON) dot1 = 0.0;

if (fabs(dot2) <= EPSILON) dot2 = 0.0;

if (fabs(dot3) <= EPSILON) dot3 = 0.0;

536 Chapter 11 Intersection in 3D

(a) (b)

(d)(c)

Figure 11.26 Plane-triangle intersection conﬁgurations.

d1d2 = dot1 * dot2;

d1d3 = dot1 * dot3;

if (d1d2 > 0.0 && d1d3 > 0.0) {

// all points above plane

return false;

} else if (d1d2 < 0.0 && d1d3 < 0.0) {

// all points below plane

return false;

}

if (fabs(dot1) + fabs(dot2) + fabs(dot3) == 0) {

// coplanar case

isect.type = plane;

return true;

}

11.5 Planar Components 537

// Most common intersection

if ((dot1>0&&dot2>0&&dot3<0)||

(dot1<0&&dot2<0&&dot3>0){

isect.type = line;

Line3D l1(tri.p1, tri.p3);

Line3D l2(tri.p2, tri.p3);

Point3D point1, point2;

LineIntersectPlane(plane, l1, point1);

LineIntersectPlane(plane, l2, point2);

isect.line.d = point2 - point1;

isect.line.p = point1;

return true;

}

if ((dot2>0&&dot3>0&&dot1<0)||

(dot2<0&&dot3<0&&dot1>0){

isect.type = line;

Line3D l1(tri.p2, tri.p1);

Line3D l2(tri.p3, tri.p1);

Point3D point1, point2;

LineIntersectPlane(plane, l1, point1);

LineIntersectPlane(plane, l2, point2);

isect.line.d = point2 - point1;

isect.line.p = point1;

return true;

}

if ((dot1>0&&dot3>0&&dot2<0)||

(dot1<0&&dot3<0&&dot2>0){

isect.type = line;

Line3D l1(tri.p1, tri.p2);

Line3D l2(tri.p3, tri.p2);

Point3D point1, point2;

LineIntersectPlane(plane, l1, point1);

LineIntersectPlane(plane, l2, point2);

isect.line.d = point2 - point1;

isect.line.p = point1;

return true;

}

// Case b

if (dot1 == 0 && ((dot2>0&&dot3 > 0) || (dot2<0&&dot3 < 0))) {

isect.type = point;

538 Chapter 11 Intersection in 3D

isect.point = tri.p1;

return true;

}

if (dot2 == 0 && ((dot1>0&&dot3 > 0) || (dot1<0&&dot3 < 0))) {

isect.type = point;

isect.point = tri.p2;

return true;

}

if (dot3 == 0 && ((dot2>0&&dot1 > 0) || (dot2<0&&dot1 < 0))) {

isect.type = point;

isect.point = tri.p3;

return true;

}

// Case c

if (dot1 == 0 && ((dot2>0&&dot3 < 0) || (dot2<0&&dot3 > 0))) {

isect.type = line;

Line3D l1(tri.p3, tri.p2);

Point3D point1;

LineIntersectPlane(plane,l1, point1);

isect.line.d = point1 - tri.p1;

isect.line.p = tri.p1;

return true;

}

if (dot2 == 0 && ((dot1>0&&dot3 < 0) || (dot1<0&&dot3 > 0))) {

isect.type = line;

Line3D l1(tri.p1, tri.p3);

Point3D point1;

LineIntersectPlane(plane,l1, point1);

isect.line.d = point1 - tri.p2;

isect.line.p = tri.p2;

return true;

}

if (dot3 == 0 && ((dot1>0&&dot2 < 0) || (dot1<0&&dot2 > 0))) {

isect.type = line;

Line3D l1(tri.p1, tri.p2);

Point3D point1;

LineIntersectPlane(plane, l1, point1);

isect.line.d = point1 - tri.p3;

isect.line.p = tri.p3;

11.5 Planar Components 539

return true;

}

// Case d

if (dot1 == 0 && dot2 == 0) {

isect.type = line;

isect.line.d = tri.p2 - tri.p1;

isect.line.p = tri.p1;

return true;

}

if (dot2 == 0 && dot3 == 0) {

isect.type = line;

isect.line.d = tri.p3 - tri.p2;

isect.line.p = tri.p2;

return true;

}

if (dot1 == 0 && dot3 == 0) {

isect.type = line;

isect.line.d = tri.p3 - tri.p1;

isect.line.p = tri.p1;

return true;

}

return false;

}

11.5.4 Triangle and Triangle

In this section we address the problem of intersecting two triangles. For the purposes

of this section, we deﬁne our two triangles as sets of three vertices:

: {V

0,0

, V

0,1

, V

0,2

}

: {V

1,0

, V

1,1

, V

1,2

}

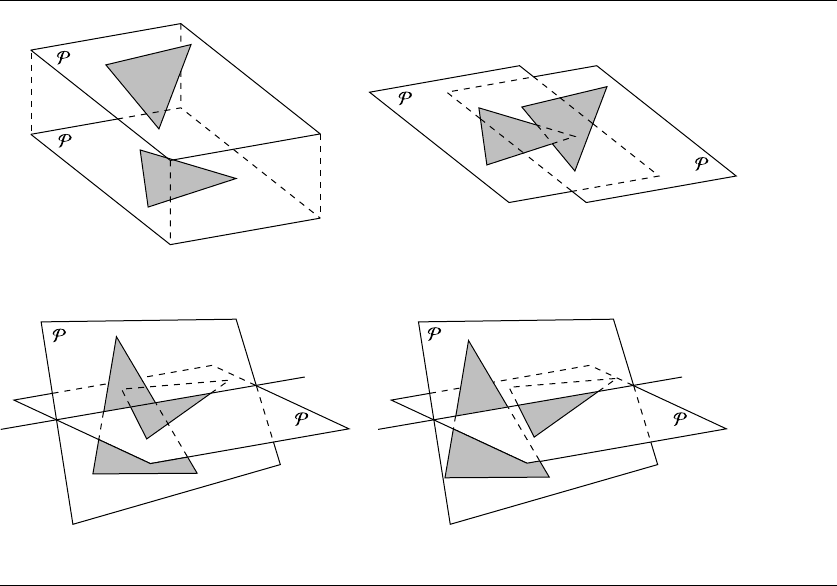
There are a number of different conﬁgurations that a triangle-triangle intersection

method must handle (see Figure 11.27): the planes P

and P

may be parallel and

noncoincident, parallel but coincident, or nonparallel, with T

and T

intersecting

or not. Irrespective of the algorithm, the coincident-plane conﬁguration must be

handled as a special case (more on this later), as should cases where the triangles

themselves are degenerate in some fashion (two or more vertices coincident).

540 Chapter 11 Intersection in 3D

(a) (b)

Figure 11.27 Triangle-triangle intersection conﬁgurations: (a) P

P

, but P

= P

; (b) P

= P

;

intersects T

; (d) T

does not intersect T

The most obvious algorithm is to simply test if each edge of each polygon inter-

sects the other triangle (face): when the ﬁrst edge-face intersection is found, return

true; if no edge-face intersections are found, return false. Given an efﬁcient line

segment–triangle intersection routine, this isn’t too bad; however, several other al-

gorithms are notably faster.

oller and Haines describe the “interval overlap method” for determining if two

triangles intersect (M

oller and Haines 1999; M

oller 1997); if there is an intersec-

tion, the line segment of the intersection is available fairly directly. The fundamental

insight upon which their method is based is this: If we’ve already rejected pairs of tri-

angles whose vertices are entirely on one side of each other’s plane, then the line L

at which the planes intersect will also intersect both triangles; the plane intersection

line L is “clipped” by each triangle into two line segments (“intervals”). If these two

line segments overlap, then the triangles intersect; otherwise, they do not. The line L

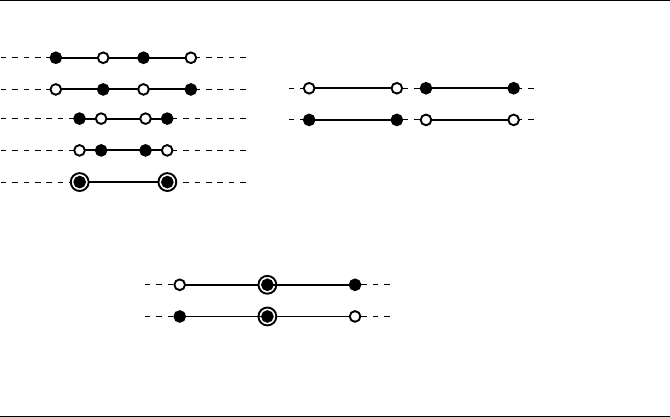
is easily computed (see Section 11.5.1), giving us

11.5 Planar Components 541

(c)

(a) (b)

0,0

1,0

0,1

1,1

Figure 11.28

Triangle-triangle interval overlap conﬁgurations: (a) intersection; (b) no intersec-

tion; (c) ?.

L(t) = P + t



Let t

0,0

and t

0,1

be the parameter values on L describing the segment intersected by

, and t

1,0

and t

1,1

be the parameter values on L describing the segment intersected

by T

. Figure 11.28 shows the possible relationships between the intervals. Clearly,

we can easily reject nonintersecting triangles (although, as the ﬁgure illustrates, you

must make a “policy” decision when the intervals abut exactly) and only compute the

actual intersection once an intersection has been detected, and then only if we wish

to know more than whether an intersection occurred.

Earlier, it was noted that we assumed the vertices of each triangle had been

checked against the plane of the other, in order to do a quick reject on triangles that

could not possibly intersect. The interval overlap method does this by checking the

signed distance of each point from the other triangle’s plane (see Section 10.3.1). This

signed distance can now be put to use again: we know that one vertex of each triangle

lies on the opposite side of L than the other two (rarely, one or two of the vertices of

a triangle may actually be on L exactly, but this adds only a little bit of extra logic to

the implementation). Without loss of generality, assume that V

0,0

and V

0,1

lie on one

side of L.

Now, it would be certainly possible to ﬁnd the points on L where the edges

0,0

0,2

and V

0,1

0,2

intersect it, by simply computing the intersection points of two

3D lines, but M

oller and Haines employ a clever optimization:

542 Chapter 11 Intersection in 3D

1. Project the triangle vertices V

0,i

onto L:



0,i



d · (V

0,i

− P), i ∈{0, 1, 2}

2. Compute t

0,0

and t

0,1

as follows:

0,i

= V



0,i

+ (V



0,2

− V



0,i

)

dist

0,i

dist

0,i

− dist

0,2

, i ∈{0, 1}

If the actual intersection line segment is desired, then we can ﬁnd the overlapping

interval by inspecting t

0,0

, t

0,1

, t

1,0

, and t

1,1

, and then plugging the parameter values

back into the equation for L.

An outline of the entire algorithm is as follows:

1. Determine if either T

or T

(or both) are degenerate, and handle in application-

dependent fashion (this may mean exiting the intersection algorithm, or not).

2. Compute the plane equation of T

3. Compute the signed distances dist

1,i

, i ∈{0, 1, 2}, of the vertices of T

4. Compare the signs of dist

1,i

, i ∈{0, 1, 2}: if they are all the same, return false;

otherwise, proceed to the next step.

5. Compute the plane equation of T

6. If the plane equations of P

and P

are the same (or rather, within 1), then

compare the d values to see if the planes are coincident (within 1):

– If coincident, then project the triangles onto the axis-aligned lane that is most

nearly oriented with the triangles’ plane, and perform a 2D triangle intersec-

tion test.

– Otherwise, the parallel planes are not coincident, so no possible intersection;

exit the algorithm.

7. Compare the signs of dist

0,i

, i ∈{0, 1, 2}: if they are all the same, return false;

otherwise, proceed to the next step.

8. Compute intersection line.

9. Compute intervals.

– If no interval overlap, triangles don’t intersect. Return false.

– Otherwise, if intersecting line segment is required, compute it. In any case,

return true.

3. The method of separating axes (Section 7.7) can be used to determine whether or not an

intersection exists. Generally speaking, the intersection of two 2D triangles will be one or

more line segments (which may degenerate to a point); if this information is required (rather

than merely determining whether or not an intersection exists), then we can compute the

intersection of each edge of each triangle against the other triangle.

11.6 Planar Components and Polyhedra 543

11.6 Planar Components and Polyhedra

In this section we discuss the intersection of planar components and polyhedra,

which are a special type of polygonal mesh (or polymesh). A polygonal mesh is a

collection of vertices, edges, and faces that satisiﬁes the following conditions:

i. Each vertex must be shared by at least one edge. (No isolated vertices are allowed.)

ii. Each edge must be shared by at least one face. (No isolated edges or polylines

allowed.)

iii. If two faces intersect, the vertex or edge of intersection must be a component in

the mesh. (No interpenetration of faces is allowed. An edge of one face may not

live in the interior of another face.)

Faces are convex polygons that live in 3D. Many applications support only trian-

gular faces because of their simplicity in storage and their ease of use in operations

applied to collections of the faces. It is possible to allow nonconvex polygon faces, but

this only complicates the implementation and manipulation of the objects. If all the

faces are triangles, the object is called a triangle mesh, or in short a trimesh.

A polyhedron (plural is polyhedra) is a polymesh that has additional constraints.

The intuitive idea is that a polyhedron encloses a bounded region of space and that it

has no unnecessary edge junctions. The simplest example is a tetrahedron, a polymesh

that has four vertices, six edges, and four triangular faces. The additional constraints

are

The mesh is connected when viewed as a graph whose nodes are the faces and

whose arcs are the edges shared by adjacent faces. Intuitively, a mesh is connected

if you can reach a destination face from any source face by following a path of

pairwise adjacent faces from the source to the destination.

Each edge is shared by exactly two faces. This condition forces the mesh to be a

closed and bounded surface.

11.6.1 Trimeshes

If the polyhedron’s faces are all triangular, then the problem of intersecting the poly-

hedron with a plane or a triangle is relatively straightforward: we can simply apply

the triangle-plane intersection algorithm (Section 11.5.3) or the triangle-triangle in-

tersection algorithm (Section 11.5.4) to each triangular face of the polyhedron. Some

efﬁciency may be gained by noting that a number of the operations involving the tri-

angle mesh’s vertices (e.g., checking which side of the plane a vertex is on) need be

done only once.