Schneider P., Eberly D.H. Geometric Tools for Computer Graphics

Подождите немного. Документ загружается.

544 Chapter 11 Intersection in 3D

nˆ

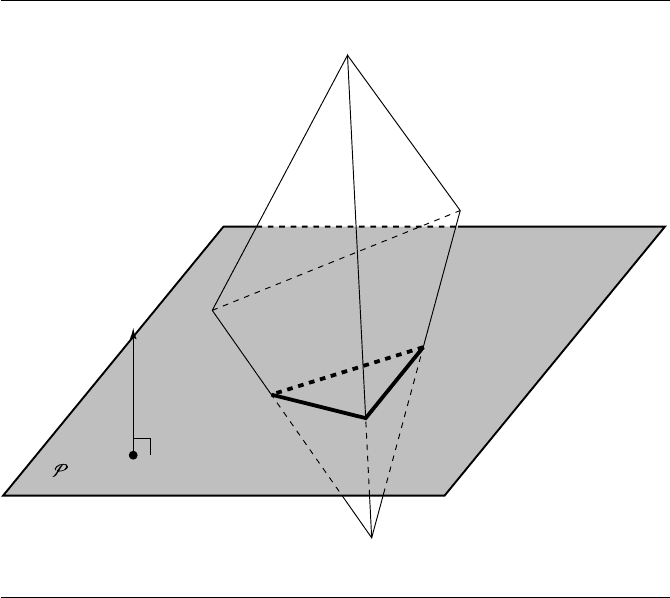
Figure 11.29 Intersection of a trimesh and a plane.

In general, the intersection of a triangle mesh and a plane or triangle will consist

of a union of vertices, edges, and polylines (open or closed). Figure 11.29 shows a

trimesh (a tetrahedron, in this case) intersecting a plane P; the bold polyline shows

the intersection, consisting of three line segments, which connect to form a polyline.

11.6.2 General Polyhedra

By our deﬁnition, a polyhedron may have faces with an arbitrary number of sides,

subject only to the restriction that the faces be convex. If we wish to intersect such a

polyhedron with a plane or triangle, then we’re going to have to solve the problem

of intersecting a polygon with a plane or with a triangle. If we then apply the same

approach as just described for intersecting trimeshes with planes and triangles, then

we’ll have again a union of vertices, edges, and polylines.

11.6 Planar Components and Polyhedra 545

nˆ

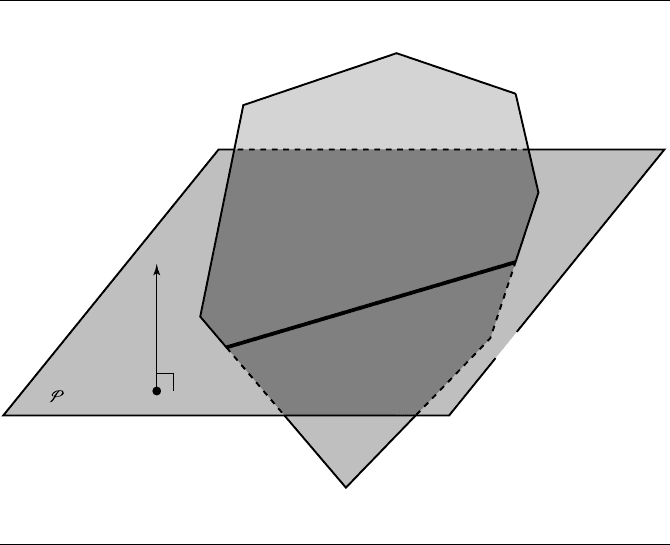
Figure 11.30

Intersection of a polygon and a plane.

Planes and Polygons

Figure 11.30 shows a convex polygon intersecting a plane P. The edges V

and V

intersect the plane, and the intersection consists of a single line (shown in bold). The

method for solving this is a simple generalization of the technique for intersecting

a triangle and a plane (Section 11.5.3): If the plane and the plane containing the

polygon are not parallel, then there is possibly an intersection. We compute the

signed distance from each of V

, V

, ..., V

n−1

, and if the signs differ, then we have

an intersection. The edge V

i+1

intersects the plane if the two vertices have different

signs; there will be of course two such edges if there is an intersection; however, care

must be taken if one or more vertices occur exactly in the plane.

Triangles and Polygons

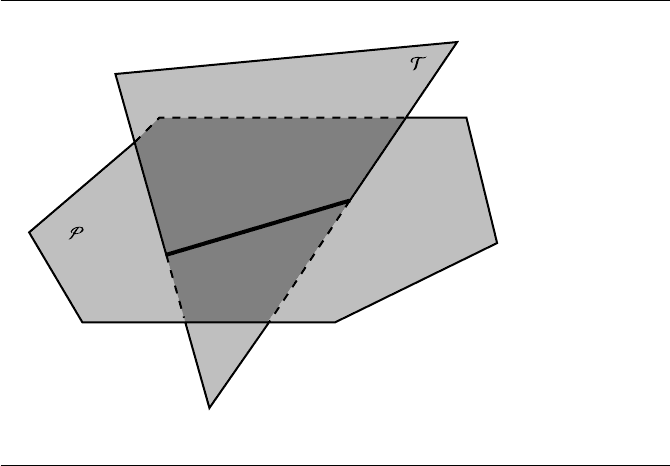
Figure 11.31 shows a convex polygon P intersecting a triangle T. Again we can

ﬁrst check if the plane of the polygon and the plane of the triangle are parallel, to

determine if any intersection is possible. If an intersection is possible, then we can

546 Chapter 11 Intersection in 3D

Figure 11.31 Intersection of a polygon and a triangle.

again compute the signed distances from the P’s plane to the vertices of T in order

to see if the triangle itself crosses the polygon’s plane. However, the polygon and the

plane may or may not intersect at this point; we have to check the edges of both the

triangle and the polygon against the other to see if any edge penetrates the face of

the other object. We can optimize this a little by noting that we only have to check

edges V

i+1

if the signs of the vertices differ. When checking the edge of the polygon

against the triangle, we can easily use the method described in Section 11.1.2 to see if

the edge intersects the interior of the triangle. However, to check whether an edge

i+1

intersects the interior of the polygon, we have to utilize the less efﬁcient

method of line segment/polygon intersection described in Section 11.1.3.

Planar Components and Polyhedra

In order to determine the intersection of a planar component and a polyhedron,

we simply apply the triangle-polygon or plane-polygon intersection methods just

described to each face of the polyhedron. Note again that some efﬁciency can be

gained by computing the signed distances of all the vertices prior to testing each face,

so that the same signed distance isn’t recomputed as each face is tested.

11.7 Planar Components and Quadric Surfaces 547

11.7 Planar Components and Quadric Surfaces

In this section, we cover the intersection of planar components and quadric surfaces.

We present several different solutions—one for the general case of a plane and any

quadric, one for the case of a plane and the so-called “natural quadrics” (sphere, right

circular cone, right circular cylinder), and one for the intersection of a triangle and a

cone.

11.7.1 Plane and General Quadric Surface

In this section we address the problem of computing the intersection of a plane and

a general quadric surface (Busboom and Schalkoff 1996). The solution presented

holds for all quadric surfaces, but because it is general, it cannot take advantage of

geometric characteristics of particular types of quadrics. Methods for handling some

particular quadrics are covered in subsequent sections.

A general quadric surface can be described as

+ by

+ cz

+ 2fyz +2gzx + 2hyx + 2px + 2qy + 2rz + d = 0 (11.17)

The particular values of the coefﬁcients a, b, c, d, e, f , g, h, p, q, and r determine the

type of quadric (see Section 9.4).

For the purposes of this problem, we’ll deﬁne a plane by specifying a point P on

the plane and two orthogonal vectors u and v in the plane:

P(t

, t

) = P +t

u + t

v (11.18)

The intersection of the plane with the quadric surface is obtained by substituting

Equation 11.18 into Equation 11.17. This yields a quadratic equation in terms of t

and t

+ Bt

+ Ct

+ Dt

+ Et

+ F = 0 (11.19)

The problem, then, consists in ﬁnding the coefﬁcients A, B, C, D, E, and F .

Rather than writing out this very large algebraic expression, we’ll take a slightly

different approach: if we represent the sets of coefﬁcients of Equations 11.17 and

11.19 as matrices, then we can express the transformation as a matrix. Let

C =

[

ABCDEF

]

and

Q =

[

abcf ghpqrd

]

548 Chapter 11 Intersection in 3D

nˆ

Figure 11.32 Intersection of a plane and a sphere.

Then, our transformation is the matrix M satisfying

C = MQ

which is

M =







0000

2(u

+ v

) 2(u

+ v

) 2(u

+ v

) 0000

0000

2(P

+ u

) 2(P

+ u

) 2(P

+ u

) 2u

2(P

+ v

) 2(P

+ v

) 2(P

+ v

) 2v







11.7.2 Plane and Sphere

In this section we address the problem of computing the intersection of a plane and

a sphere, as shown in Figure 11.32.

A sphere can be deﬁned implicitly:

(x −C

)

+ (y − C

)

+ (z − C

)

− r = 0 (11.20)

11.7 Planar Components and Quadric Surfaces 549

where C is the center of the sphere and r is the radius. If we deﬁne a plane paramet-

rically, as we did in Section 9.2.1

P(t

, t

) = P +t

u + t

v

we can substitute this equation into Equation 11.20, giving us a quadratic curve of

the form

+ Bt

+ Ct

+ Dt

+ Et

+ F = 0

If we do the substitution, expand, and collect terms, we have

A = u

+ u

B = 2(u

+ u

)

C =v

+ v

D = 2(P

+ P

) − 2(C

+ C

)

E =2(P

+ P

) − 2(C

+ C

)

F = C

+ C

+ P

+ PC

− 2(C

+ C

) − r

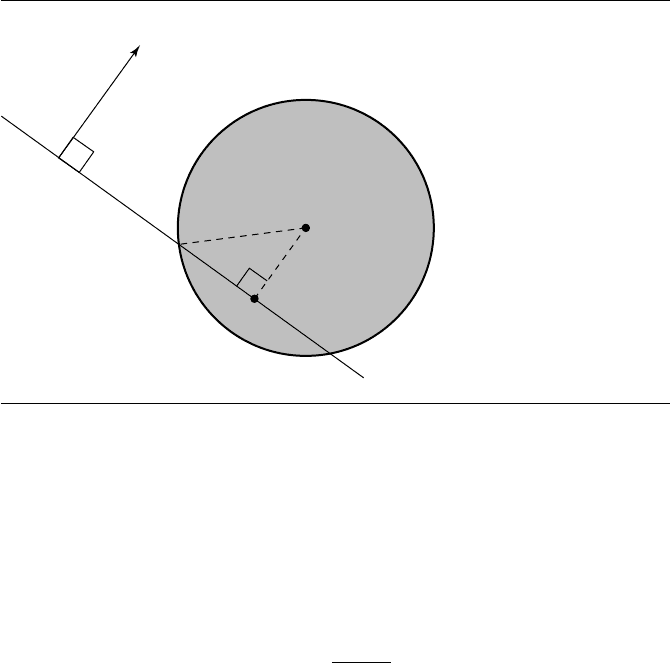
An alternative is to use a more direct geometric approach. Clearly, the intersection

of a plane and a sphere, if it exists, is simply a circle lying in the plane. The plane’s

equation provides part of a 3D circle speciﬁcation, so we need to ﬁnd the circle’s

center and radius. The insight for the solution lies in observing that the center C

of the sphere is located at some distance along a line that passes through the center

of the circle Q of intersection and is normal to the plane P, as can be seen more

directly in cross section in Figure 11.33. If our plane P is given in the normalized

coordinate-free version of the implicit form

P ·ˆn + d = 0

then the distance between the plane and the center of the sphere can be simply

written as

b =ˆn · Q + d

(see Section 10.3.1). If |b| >r, then there is no intersection; otherwise, the center of

the circle of circle Q is simply

Q = C − b ˆn

550 Chapter 11 Intersection in 3D

nˆ

Figure 11.33 Cross-sectional view of sphere-plane intersection.

All that remains is for us to determine the radius of the circle of intersection.

Again looking at Figure 11.33, we can easily see that

+ b

= r

and so

a =



− b

is the radius.

If the plane just barely “grazes” the sphere, then r

− b

will be a very small

number; in this case, the application may wish to consider that the intersection is

actually just a point and act accordingly.

The pseudocode is

bool PlaneSphereIntersection(Plane3D plane, Sphere sphere, Intersection isect)

{

Vec3D v1 = sphere.center - plane.pointOnPlane;

// normal is unit length

float b = fabs(dotProd(plane.normal,v1));

if(b<r){

Point3D Q = sphere.center-b*plane.normal;

float radius = sqrt(sphere.radius^2 + b^2);

11.7 Planar Components and Quadric Surfaces 551

Figure 11.34 Intersection of a plane and a cylinder.

if (radius < epsilon) {

// consider it as a point

isect.point = Q;

isect.type = point;

} else {

isect.center = Q;

isect.radius = radius;

isect.type = circle;

}

return true;

}

return false;

}

11.7.3 Plane and Cylinder

In this section we address the problem of the intersection of a plane and a cylinder,

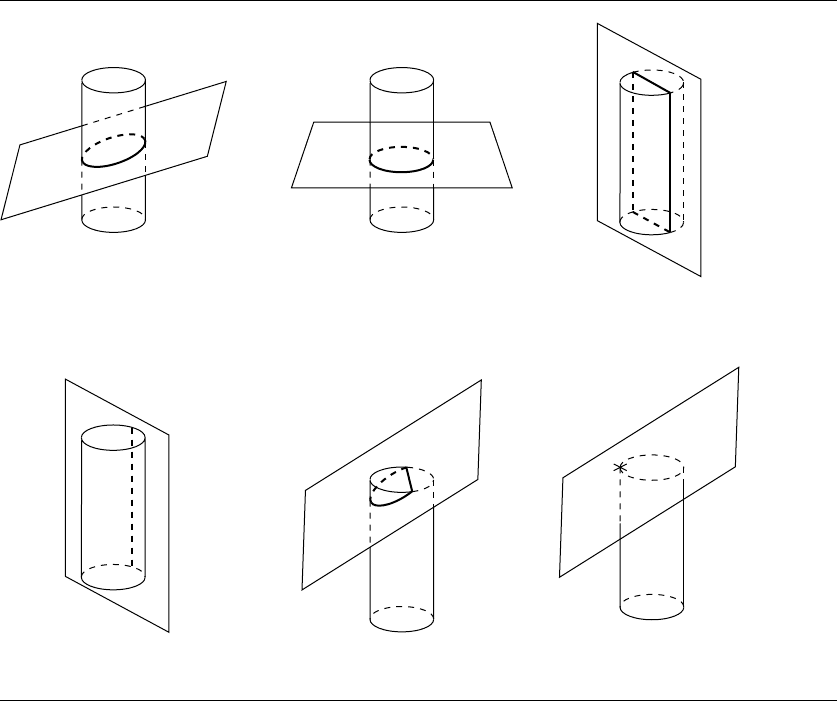
as shown in Figure 11.34. There are actually quite a number of ways a cylinder and a

plane can intersect, six of which are shown in Figure 11.35. Note that the intersections

are shown for a ﬁnite cylinder. An inﬁnite cylinder has fewer intersection conﬁgura-

tions (we don’t need to deal with the end caps); possible intersections are a circle, an

ellipse, a single line, or a pair of lines. We give algorithms for intersection detection

of a plane and an inﬁnite cylinder and for a plane and a ﬁnite cylinder; the former

552 Chapter 11 Intersection in 3D

Ellipse Circle Quadrilateral

Line PointElliptical arc/line segment

Figure 11.35

Some of the ways a plane and a cylinder can intersect.

is somewhat simpler. In a later section, we’ll give an algorithm for computing the in-

tersection of a plane and an inﬁnite cylinder. These algorithms can be extended to a

ﬁnite cylinder by “clipping” the extent of the conic intersection curve or lines by the

planes containing the end caps.

Intersection Detection

For the intersection detection algorithm, we’ll deﬁne a plane implicitly:

P ·ˆn + d = 0

11.7 Planar Components and Quadric Surfaces 553

(The coordinatized version is the usual ax +by +cz +d =0, where ˆn =[

abc

]

and

√

+ b

+ c

= 1.) The cylinder is deﬁned in “general position”—as a center-

point C, axis

d, and half-height h (see Figure 11.12 in Section 11.3.4).

Inﬁnite Cylinder

For the purposes of detecting an intersection, a plane P and an inﬁnite cylinder C

can be in one of several conﬁgurations:

1. If P is parallel to C’s axis, then there will be an intersection if the distance between

P and C is less than or equal to the radius of the cylinder.

2. If P is not parallel to C’s axis,

d ·ˆn =1, there will always be an intersection.

Finite Cylinder

For the purposes of detecting an intersection, a plane P and a cylinder C can be in

one of several conﬁgurations:

1. P may be parallel to C’s axis: |

d ·ˆn|=1.

2. P may be perpendicular to C’s axis:

d ·ˆn =0.

3. P may be neither parallel nor perpendicular to C’s axis. In this case, P may or

may not intersect C.

Let’s consider these cases one by one:

1. If P is parallel to C’s axis, then there will be an intersection if the distance between

P and C’s axis is less than or equal to the radius of the cylinder (in which case the

intersection will be a quadrilateral or a single line, respectively).

2. If P is perpendicular to C’s axis, then there will be an intersection if the distance

between P and C is less than or equal to the half-height of the cylinder (in which

case the intersection will be a circle).

3. If P is neither parallel nor perpendicular to C’s axis, then there are two cases to

consider:

a. The intersection of P and the axis of C is closer to the centerpoint of C than

the half-height; in this case, there is deﬁnitely an intersection.

b. P intersects the axis of C outside the end caps of the cylinder, in which case

there may or may not be an intersection, depending on the relative location

of the point of intersection and the angle between the plane and the axis.

In either case, the intersection will be either an ellipse, an elliptical arc and a

straight line, or two elliptical arcs and two straight lines, depending on the relative

orientation of the plane.