Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

664 Chapter 12 Miscellaneous 3D Problems
Q
Q'
r
n
rn
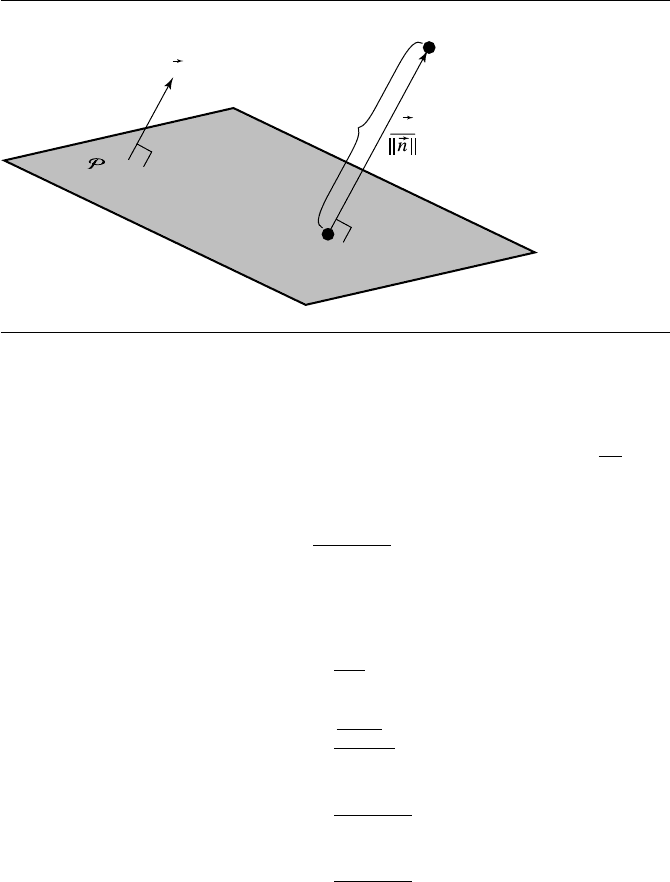
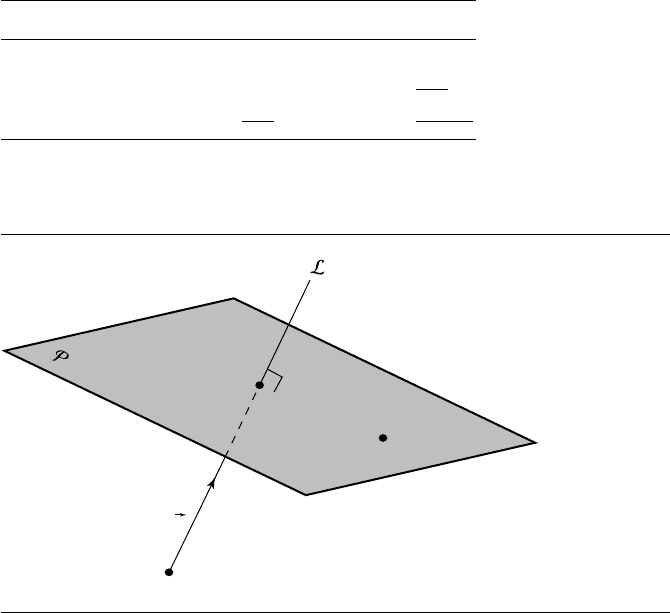
Figure 12.1 Projection of a point onto a plane.
But Q
·n =−d because by definition Q
lies on P and n ·n =n
2
,so
r n
n
·n =
rn. If we substitute these into Equation 12.2 and solve for r,weget
r =
Q ·n +d
n
(12.3)
We can then rearrange Equation 12.1 and substitute Equation 12.3:
Q
= Q −
r n
n
= Q −
Q·n+d
n
n
n
= Q −
Q ·n +d
nn
n
= Q −
Q ·n +d
n ·n
n
If the plane equation is normalized, we have ˆn=1, and thus the division can be
avoided:
Q
= Q −
Q ·ˆn +d
ˆn
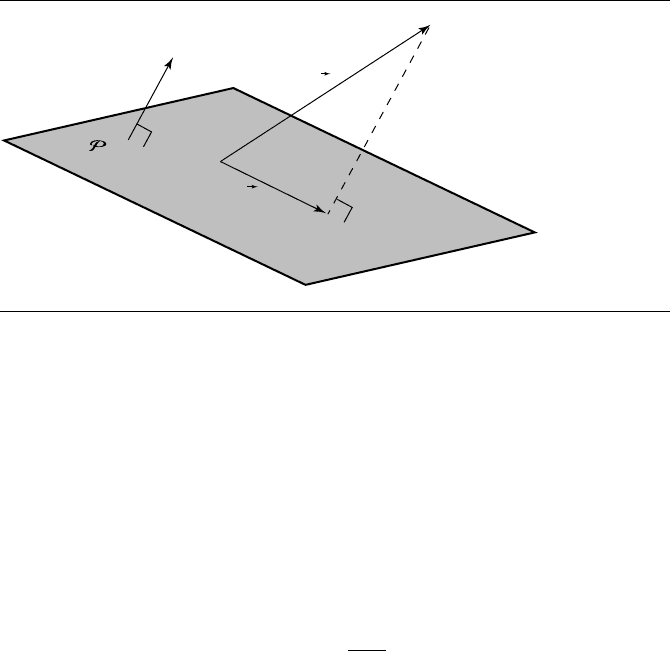
12.2 Projection of a Vector onto a Plane 665
v
w
ˆn
Figure 12.2 Projection of a vector onto a plane.
12.2 Projection of a Vector onto a Plane
Theprojectionofavectorv onto a plane P : P ·ˆn + d = 0, as shown in Figure 12.2,
is
w =v − (v ·ˆn) ˆn (12.4)
or
w =v −
v ·n
n
2
n
if the plane normal is not unit length.
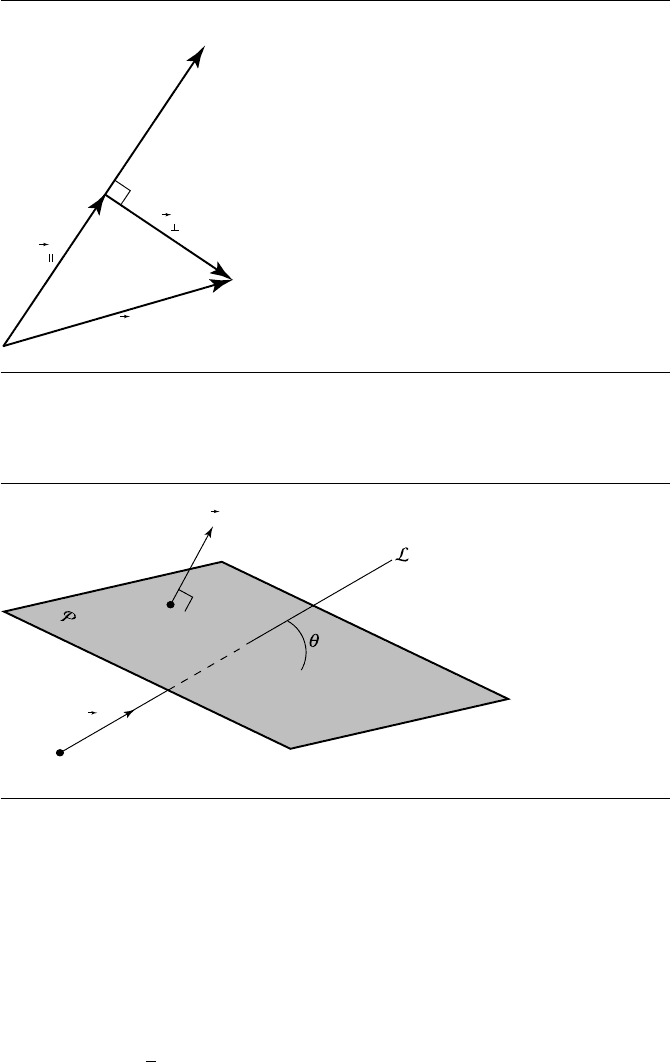
To see why this is so, consider Figure 12.3. Here, we see the projection of v
onto ˆu.Thevectorv can be decomposed into v =v
⊥
+v
, components parallel and
perpendicular, respectively, to ˆu. By the definition of the dot product, the length of
v
is v ·ˆu, and because the two components’ sum is v,wehave
v
= (v ·ˆu) ˆu (12.5)
v
⊥
=v −(v ·ˆu) ˆu (12.6)
If we consider the vector ˆu from Figure 12.3 to be the plane normal ˆn from
Figure 12.2, then we can see that w =v
⊥
, and so Equation 12.4 follows from Equa-
tion 12.5 directly. The insight here is to realize that the projection of v onto P is the
same for any plane perpendicular to ˆn, and so you can thus understand why the d
component of the plane equation for P does not appear in the solution.
666 Chapter 12 Miscellaneous 3D Problems
v
v
v
û
Figure 12.3 Projection of one vector onto another.
d
n
P
0
P
1
Figure 12.4 Angle between a line and a plane.
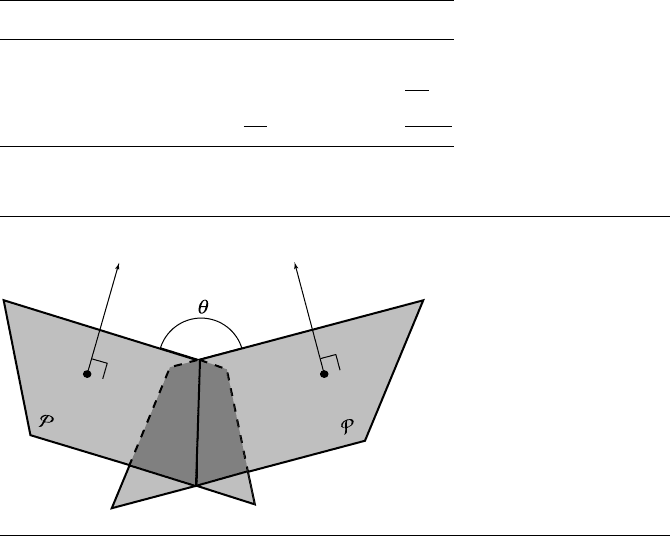
12.3 Angle between a Line and a Plane
The angle between a line L(t) = P
0
+ t
d and a plane P : P
1
·n + d = 0 can be
computed in one of several ways, depending on whether the line, the plane, both,
or neither are normalized (see Figure 12.4). The formula for φ, the angle between the
plane normal and the line, is given in Table 12.1. The angle between the line and the
plane itself is θ =
π
2
− φ.
12.5 Plane Normal to a Line and through a Given Point 667
Table 12.1
Formula for φ.
Plane Line
Normalized Nonnormalized
Normalized φ =arccos(ˆn ·
ˆ
d) φ = arccos
ˆn·
d
d
Nonnormalized φ = arccos
n·
ˆ
d
n
φ =arccos
n·
d
n
d
P
0
P
1
n
1
1
0
ˆn
0
ˆ
Figure 12.5 Angle between two planes.
12.4 Angle between Two Planes
The angle between two planes P
0
: {P
0
, n
0
}and P
1
: {P
1
, n
1
}(see Figure 12.5) can eas-
ily be computed by the angle between their two normals. As with the angle between
a line and a plane, the angle θ between the two planes can be computed in one of
several ways, depending on whether P
0
, P
1
, both, or neither are normalized (see
Table 12.2).
12.5 Plane Normal to a Line and through
a Given Point
Suppose we have a line L(t) = P + t
d and a point Q (see Figure 12.6). The plane
normal to L, going through Q,is
d
x
x +d
y
y +d
z
z − (d
x
Q
x
+ d
y
Q
y
+ d
z
Q
z
) = 0
668 Chapter 12 Miscellaneous 3D Problems
Table 12.2 Formula for θ.
P
0
P
1
Normalized Nonnormalized
Normalized θ = arccos( ˆn
0
·ˆn
1
)θ= arccos
ˆn
0
·n
1
n
1
Nonnormalized θ =arccos
n
0
·ˆn
1
n
0
θ = arccos
n
0
·n
1
n
0
n
1
d
P
Q
Figure 12.6 Plane normal to a line through a point.
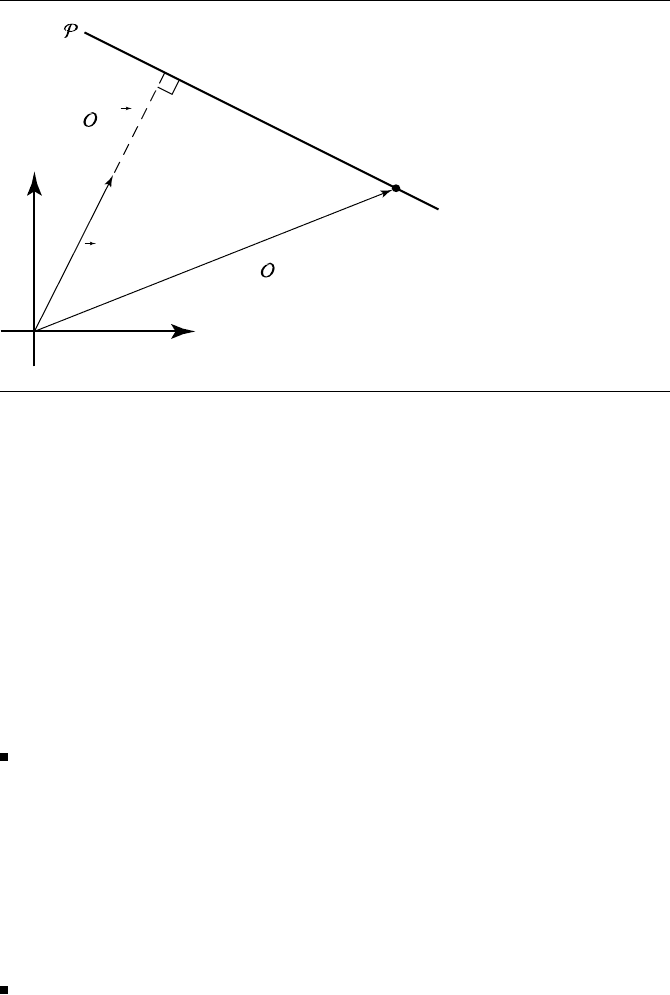
The normal to P is obviously just the direction vector for L.Thed coefficient
for P may not be quite so obvious. However, consider the “cross section” shown
in Figure 12.7: if we draw the direction vector for L starting at the origin O, and
consider the vector
−−−→
OQ, it’s clear that the d coefficient for P is the projection of
−−−→
OQ
onto
d, and so we have
d =−(
−−−→
OQ ·
d)
which has the equivalent in component notation of
−(d
x
Q
x
+ d
y
Q
y
+ d
z
Q
z
)
12.6 Plane through Three Points 669
x
y
Q
(Q – )
• d
d
(Q – )
Figure 12.7 Computing the distance coefficient for the plane.
This equation holds true irrespective of whether or not L is normalized, and the
equation for P is normalized if and only if
d=1.
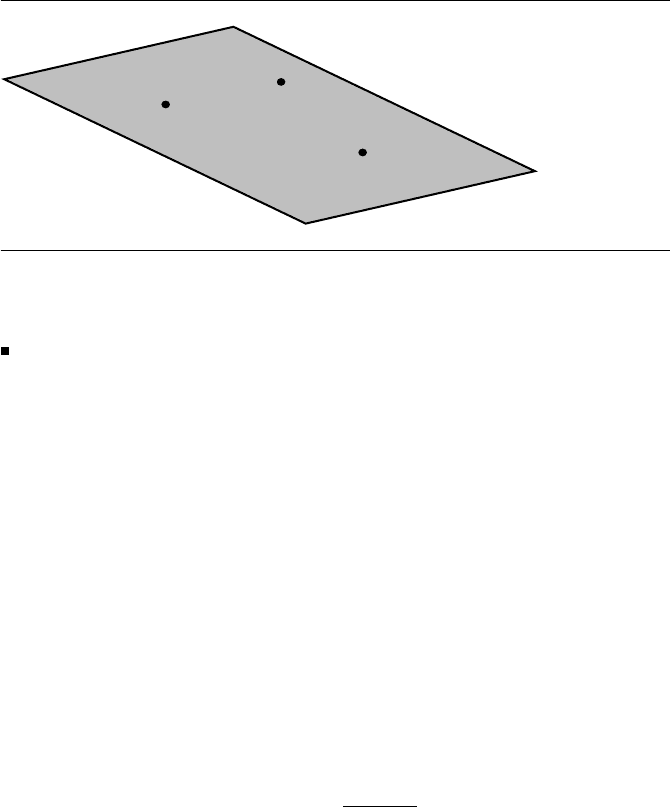
12.6 Plane through Three Points
Given three points P
0
, P
1
, and P
2
, with none coincident and not all collinear, we
can fairly directly derive the equation of the plane containing all three points (Fig-
ure 12.8). In fact, we can fairly directly derive any one of the several representations
of a plane from the three points:
Implicit: The implicit equation of a plane through three points satisfies
x −P
0,x
y −P
0,y
z − P
0,z
P
1,x
− P
0,x
P
1,y
− P
0,y
P
1,z
− P
0,z
P
2,x
− P
0,x
P
2,y
− P
0,y
P
2,z
− P
0,z
= 0
If we multiply this out, we get an equation of the form
ax + by + cz + d = 0
Parametric:
P(s, t) = P
0
+ s(P
1
− P
0
) + t(P
2
− P
0
)
670 Chapter 12 Miscellaneous 3D Problems
P
0
P
2
P
1
Figure 12.8 Three points defining a plane.
Explicit: This form requires that we specify a point on the surface, a normal,
and a third parameter d (which represents the perpendicular distance to the
origin). We have three such points from which to choose and can (as above)
compute the normal as the cross product of the vectors between two pairs of
points. Arbitrarily choosing P
0
as the point on the surface, and the normal n as
(P
1
− P
0
) × (P
2
− P
0
),wehave
P
0
·n + d = 0
Trivially,wehaved =−(P
0
·n).
12.7 Angle between Two Lines
Given two lines L
0
(t) = P
0
+t
d
0
and L
1
(t) = P
1
+t
d
1
, the angle between them can
be computed by exploiting the relationship between the dot product and angle (see
Section 3.3.1), so we have
θ = arccos
d
0
·
d
1
d
0
d
1
(12.7)
If both the line equations are normalized, this can be simplified to
θ = arccos(
ˆ
d
0
·
ˆ
d
1
)
A line’s “direction” may or may not be significant to the problem domain, partic-
ularly if the line equation defines a line, rather than a ray or line segment. The angle
computed above is between lines that “move” in the same direction. For example, if
the lines are parallel and
d
0
and
d
1
point in the same direction, then θ =0; otherwise,
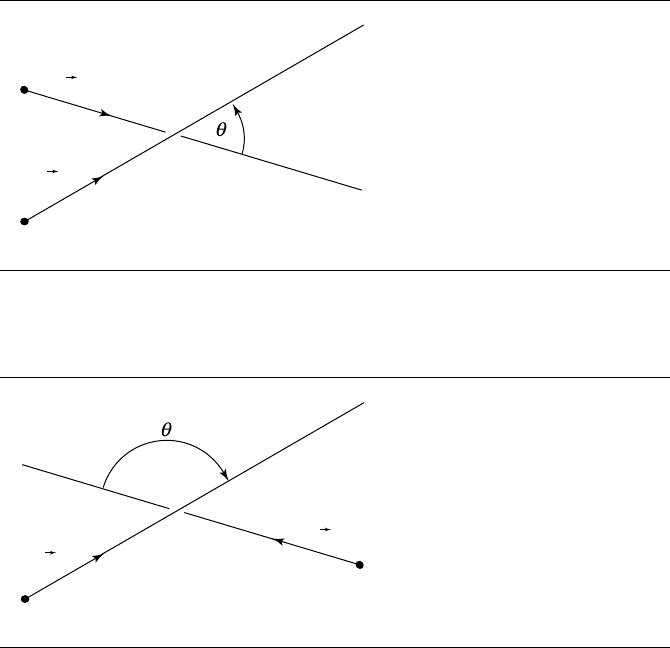
12.7 Angle between Two Lines 671
P
1
d
1
P
0
d
0
Figure 12.9 Angle between two lines in 3D.
P
1
d
1
d
0
P
0
Figure 12.10
Angle between two lines in 3D, with one line reversed.
θ = π (180
◦
). In Figure 12.9, θ ≈ 46
◦
as calculated using Equation 12.7, but if we
reverse the direction of one of the lines, as in Figure 12.10, then θ ≈ 134
◦
.
If the lines are not normalized, the pseudocode is
float Line3DLine3DAngle(Line l1, Line l2, boolean acuteAngleDesired)
{
float denominator;
denominator = Dot(l1.direction, l1.direction) *
Dot(l2.direction, l2.direction);
if (denominator < epsilon) {
// One or both lines are degenerate,
// deal with in application-dependent fashion
672 Chapter 12 Miscellaneous 3D Problems
} else {
float angle;
angle = Acos(Dot(l1.direction, l2.direction) /
Sqrt(denominator);
if (acuteAngleDesired && angle > Pi/2) {
return Pi - angle;
} else {
return angle;
}
}
}
If both lines are normalized, the pseudocode is
float Line3DLine3DAngle(Line l1, Line l2, boolean acuteAngleDesired)
{
float angle;
angle = Acos(Dot(l1.direction, l2.direction));
if (acuteAngleDesired && angle > Pi/2) {
return Pi - angle;
} else {
return angle;
}
}
Chapter
13Computational
Geometry Topics
The field of computational geometry is quite large and is one of the most rapidly
advancing fields in recent times. This chapter is by no means comprehensive. The
general topics covered are binary space-partitioning (BSP) trees in two and three
dimensions, point-in-polygon and point-in-polyhedron tests, convex hulls of finite
point sets, Delaunay triangulation in two and three dimensions, partitioning of poly-
gons into convex pieces or triangles, containment of point sets by circles or oriented
boxes in two dimensions and by spheres or oriented boxes in three dimensions, area
calculations of polygons, and volume calculations of polyhedra.
The emphasis is, of course, on algorithms to implement the various ideas. How-
ever, attention is given to the issues of computation when done within a floating-
point number system. Particular themes arising again and again are determining
when points are collinear, coplanar, cocircular, or cospherical. This is easy to do when
the underlying computational system is based on integer arithmetic, but quite prob-
lematic when floating-point arithmetic is used.
13.1 Binary Space-Partitioning Trees in 2D
The idea of partitioning space using a binary tree has its origins with Fuchs, Kedem,
and Naylor (1979, 1980) and is very useful in many applications.
Consider a line in the plane with representation n ·X −c =0. The line partitions
the plane into two half-planes. The half-plane on the side of the line to which n points
is called the positive side of the line; the other side is called the negative side of the line.
If X is on the positive side, then n · X −c>0, hence the use of the phrase “positive
673
