Schneider P., Eberly D.H. Geometric Tools for Computer Graphics
Подождите немного. Документ загружается.

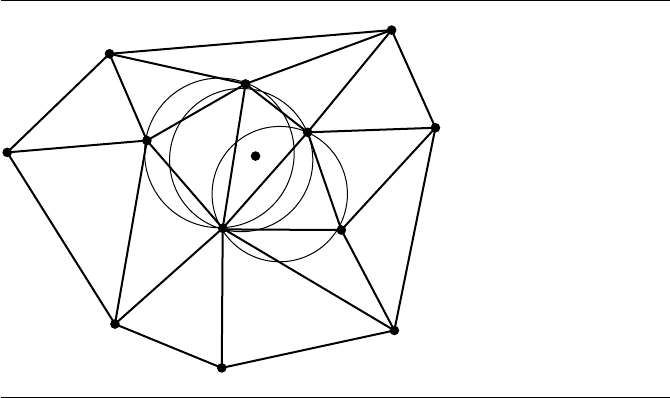
764 Chapter 13 Computational Geometry Topics
Figure 13.48 Circumcircles containing the next point to be inserted.
simpler method that just iterates over all current simplices will be easier to
program, but potentially slower for the types of data sets seen in practice (see
Figure 13.48).
b. The union of the simplices whose circumhyperspheres contain the input
point form a d-dimensional polyhedron called the insertion polyhedron.Lo-
cate the boundary faces of that polyhedron (see Figure 13.49).
c. Create new simplices by connecting the input point to the boundary faces.
Then remove the old simplices whose union was the insertion polyhedron
(see Figure 13.50).
4. After all points are inserted, those simplices that share a vertex of the supersim-
plex are removed from the mesh. The resulting mesh is the Delaunay triangula-
tion of the points (see Figure 13.51).
The 3D Delaunay triangulation can have slivers, tetrahedra that are nearly zero
volume (needlelike or flat). Researchers in recent years have made attempts to develop
methods to modify the final triangulation and obtain a good-quality one (Dey, Bajaj,
and Sugihara 1991; Cheng et al. 2000).
If the input point set has intrinsic dimensionality smaller than the space in which
the points live, probably a better approach is to use the relationship between the
Delaunay triangulation in d dimensions and the convex hull in d + 1 dimensions as
described in the next section. The convex hull algorithms appear to be better suited
for handling degeneracies in dimension than the triangulation algorithms.
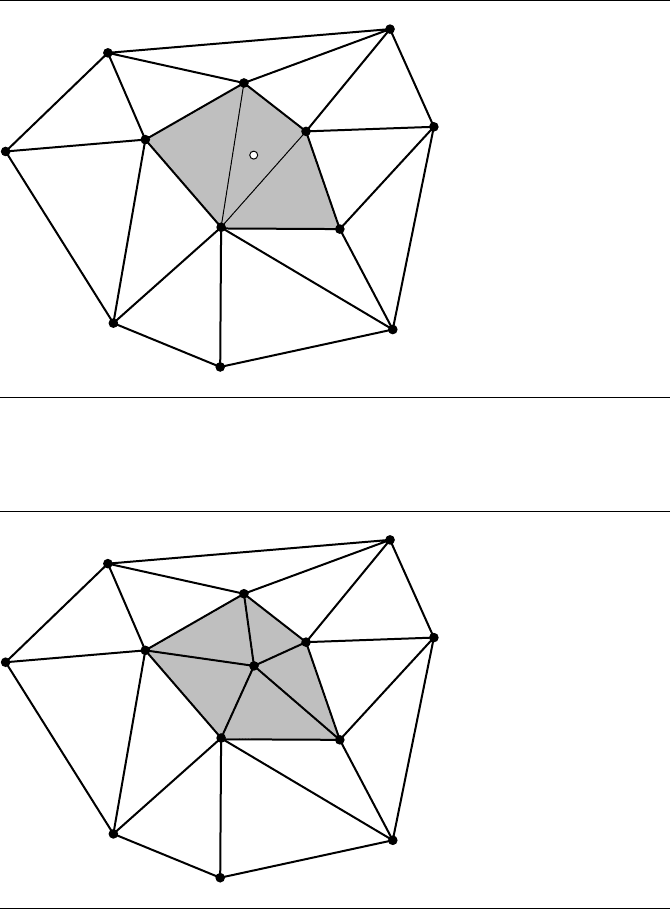
13.8 Delaunay Triangulation 765
Figure 13.49 The insertion polygon for the next point to be inserted.
Figure 13.50
The modified insertion polygon that restores the empty circumcircle condition for
the total mesh.
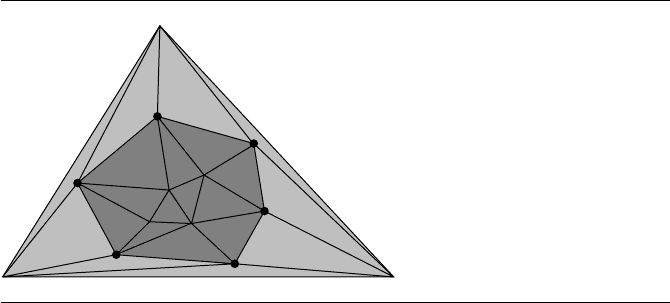
766 Chapter 13 Computational Geometry Topics
Figure 13.51 The final mesh triangles are dark gray. The removed triangles are shown in light gray.
13.8.3 Construction by Convex Hull
The Delaunay triangulation of a finite point set S ⊂R
d
for any dimension d is obtain-
able from the convex hull of S
={(X, X
2
) : X ∈ S}⊂R
d
× R = R
d+1
, as shown
in Edelsbrunner and Seidel (1986). In particular, let the convex hull be constructed so
that its hyperfaces are (d +1)–dimensional simplices. Each simplex has a normal vec-
tor in R
d
×R,say,(
N, λ). The simplices for which λ<0 form what is called the lower
hull. The other simplices form the upper hull. The projections of the simplices of the
lower hull onto R
d
are themselves simplices (of dimension d) and are the Delaunay
triangulation of S.
A simple illustration is shown in Figure 13.52 for a 2D triangulation obtained
from a 3D convex hull. The five input points are (0, 0), (0, ±1), and (1, ±1). Figure
13.52(b) shows the Delaunay triangulation. Figure 13.52(a) shows the convex hull of
the lifted points (0, 0, 0), (0, ±1, 1), and (1, ±1, 2). The lower hull consists of three tri-
angles. The counterclockwise-ordered triangle (0, 0, 0), (0, 1, 1), (1, 1, 2)has normal
vector (1, 1, −1). The third component is negative, so this triangle is on the lower hull
and is projected onto the xy-plane to obtain the counterclockwise-ordered Delaunay
triangle (0, 0), (1, 1), (0, 1). Similarly, the triangles (0, 0, 0), (1, −1, 2), (0, −1, 1)
and (0, 0, 0), (1, 1, 2), (1, −1, 2) have normals with a negative third component,
so the xy-projections of these are part of the triangulation. The counterclockwise-
ordered triangle (0, 1, 1), (0, 0, 0), (0, −1, 1)has normal vector (−2, 0, 0). The third
component is zero, so it is not part of the lower hull. The projection is a degenerate
triangle and does not contribute to the triangulation. The upper hull consists of two
triangles that are discarded.
This result is particularly useful from a numerical perspective. From experience,
implementing a convex hull algorithm that is fully robust in the presence of floating-
point numbers is easier than implementing a fully robust Delaunay triangulation
algorithm.
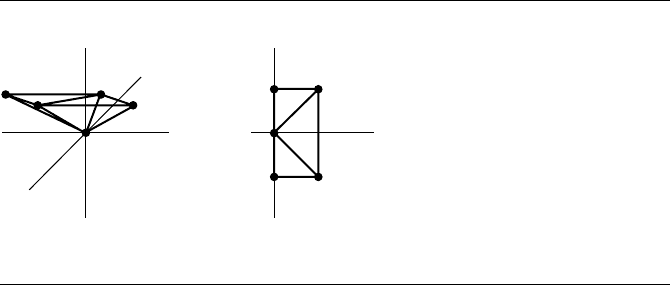
13.9 Polygon Partitioning 767
y
x
z
y
x
(a) (b)
Figure 13.52 (a) Convex hull of 2D points lifted onto a paraboloid in 3D. (b) The corresponding
Delaunay triangulation, the projection of the lower hull onto the xy-plane.
13.9
Polygon Partitioning
This section describes a few useful algorithms for partitioning a simple polygon into
triangles or into convex polygons. A key concept is that of visibility of other vertices
from a given vertex. Two vertices V
i
and V
j
are said to be visible to each other if the
open line segment connecting them is strictly inside the polygon. That is, there must
be a clear line of sight from one vertex to the other without any other portion of the
polygon blocking it, even if that portion is only a single vertex. When the two vertices
are visible to each other, the line segment connecting them is called a diagonal of the
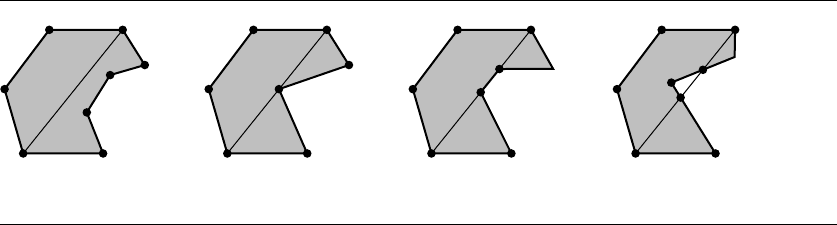
polygon. Figure 13.53 illustrates the visibility between vertices. By the definition, the
edges of the polygon are not diagonals. However, in some applications it is useful
to allow them to be labeled as such. In the discussion we distinguish between types
of vertices. A vertex is said to be a convex vertex if the angle between the two edges
sharing the vertex is smaller than π radians, as measured inside the polygon. This
angle is called the interior angle at the vertex. If the two edges sharing the vertex are
on the same line, the vertex is a collinear vertex. In typical applications, these vertices
are not allowed in construction of a polygon or are removed after some operation
modifies a polygon. If the interior angle at a vertex is larger than π radians, the vertex
is said to be a reflex vertex.
13.9.1 Visibility Graph of a Simple Polygon
Given a simple polygon with ordered vertices V
0
through V
n−1
, an undirected graph
can be constructed whose nodes represent the vertices and whose arcs represent the
diagonals of the polygon. The graph is called the visibility graph for the polygon.
In this graph, an arc connecting a vertex to itself is not allowed. If the graph is
represented as an adjacency matrix, the entry (i, j) is 1 if V
i
and V
j
are visible to
768 Chapter 13 Computational Geometry Topics
(a) (b) (c) (d)
Figure 13.53 (a) Two vertices that are visible to each other. The diagonal connecting them is shown.
(b) Two vertices that are not visible to each other, blocked by a vertex between them.
(c) Two vertices that are not visible to each other, blocked by a single edge. (d) Two
vertices that are not visible to each other, blocked by a region outside the polygon.
each other, but 0 otherwise. Of course the matrix is symmetric since the graph is
undirected. The matrix for a convex polygon consists of three zero diagonals, the
main diagonal and its sub- and superdiagonal, but all other entries are one. For other
simple polygons, the matrix can be complicated. In polygon partitions, it may be
necessary to compute part, or all, of the visibility graph.
Visibility between V
i−1
and V
i+1
For simplicity, assume that the vertex indices are computed modulo n, the number of
vertices of the polygon. Let us start with the simplest case for visibility determination.
GivenavertexV
i−1
, we wish to determine if V
i+1
is visible to it.
If V
i
is a reflex vertex, then the line segment connecting V
i−1
and V
i+1
must be
at least partially outside the polygon, so V
i−1
and V
i+1
are not visible to each other.
It suffices to consider only those V
i
that are convex vertices. For such a vertex, the
line segment V
i−1
, V
i+1
is a diagonal as long as no edges on the polygon boundary
intersect it. Geometrically equivalent is that no other vertices of the polygon lie in
the triangle V
i−1
, V
i
, V
i+1
. If the polygon has r reflex vertices and n − r convex
vertices, the obvious implementation processes each of n − r triangles and tries at
most n − 3 point-in-triangle tests. The maximum number of tests occurs when in
fact V
i−1
, V
i+1
is a diagonal. The order of the algorithm is O((n − r)n) = O(n
2
).
A more efficient implementation avoids testing all other polygon vertices for triangle
containment. If the polygon boundary intersects the segment V
i−1
, V
i+1
, then the
portion of the boundary inside the triangle must contain at least one reflex vertex.
The idea is that the polygon boundary must enter the triangle and make a turn to exit
the triangle later. The turning requires a reflex vertex. Therefore it is sufficient to test
only for containment of reflex vertices by the triangle. The order of this algorithm

13.9 Polygon Partitioning 769
R
V
0
V
1
V
2
Figure 13.54 Illustration of why lack of visibility between V
0
and V
2
is equivalent to triangle
V
0
, V
1
, V
2
containing a reflex vertex R.
is O(nr), which is better than O(n
2
) when r is much smaller than n. Figure 13.54
illustrates this idea.
If V
i−1
, V
i+2
is a diagonal of the polygon, the vertices V
i−1
, V
i
, and V
i+1
are
said to form an ear of the polygon with V
i
called the ear tip. One of the polygon
triangulation methods discussed later uses a search for ears. In Figure 13.54, vertex
V
0
is an ear tip, and the ear is the triangle formed by V
0
and its two neighboring
vertices.
Visibility between Any Two Vertices
The test for V
i
, V
j
, |i − j |≥2, being a diagonal is straightforward. The idea is to
traverse the polygon edges and test if any of them intersects the segment V
i
, V
j
.
The edges adjacent to the specified segment need not be tested. The worst-case con-
figuration is that the adjacent edge is collinear with the segment, in which case the
next edge adjacent to the current adjacent edge has an end point on the segment. The
intersection will be found by the intersection test with that edge.
If any edge of the polygon intersects the specified segment, then the segment is
not a diagonal. However, if all edges (not counting the adjacent ones to the segment)
do not intersect the segment, two situations are possible. One is that the segment is a
diagonal. The other is that the segment is outside the polygon. The diagonal testing
code must distinguish between these two. It is enough to determine the local be-
havior of the segment at only one end point, say, at V
i
. The segment is a diagonal
whenever it is contained in the cone with vertex V
i
and edges with directions V
i±1
−
V
i
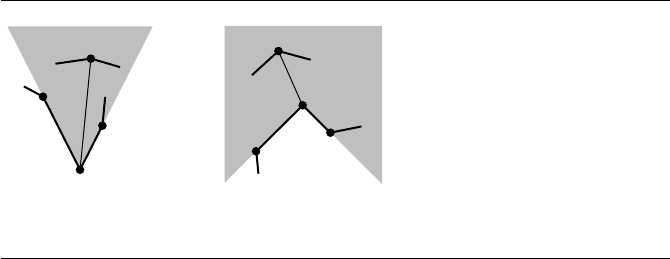
. Figure 13.55 shows the containment condition for both convex and reflex vertices.
The pseudocode for testing if V
i
0
, V
i
1
is a diagonal is listed below. The first two
inputs are the simple polygon. The last two inputs are the indices of the end points of
770 Chapter 13 Computational Geometry Topics
jj
i
i
i – 1
i – 1
i + 1
i + 1
(a) (b)
Figure 13.55 Cone containment (a) for a convex vertex and (b) for a reflex vertex.
the segment to be tested. It is assumed that |i
0
− i
1
|≥2 where modulo n arithmetic
is used for the indices.
bool IsDiagonal(int n, Point V[n], int i0, int i1)
{
// Segment may be a diagonal or may be external to the polygon. Need
// to distinguish between the two. The first two arguments of
// SegmentInCone are the line segment. The first and last two arguments
// form the cone.
iM = (i0 - 1) mod n;
iP = (i0 + 1) mod n;
if (not SegmentInCone(V[i0], V[i1], V[iM], V[iP]))
return false;
// test segment <V[i0], V[i1]> to see if it is a diagonal
for(j0=0,j1=n-1;j0<n;j1=j0,j0++) {
if (j0 != i0 && j0 != i1 && j1 != i0 && j1 != i1) {
// The first two arguments of SegmentsIntersect form a line
// segment. The last two arguments form an edge to be tested
// for intersection with the segment.
if (SegmentsIntersect(V[i0], V[i1], V[j0], V[j1]))
return false;
}
}
return true;
}
13.9 Polygon Partitioning 771
The SegmentIntersect function can be implemented based on either computing
an intersection point, if it exists, or on measuring the distance between the segments.
Sections 6.6 and 7.1 cover these topics. The
SegmentInCone function is shown in the
pseudocode below:
float Kross(Point U, Point V)
{
// Kross(U, V) = Cross((U,0), (V,0)).z
return U.x * V.y - U.y * V.x;
}
bool SegmentInCone(Point V0, Point V1, Point VM, Point VP)
{
// assert: VM, V0, VP are not collinear
Point diff = V1 - V0, edgeL = VM - V0, edgeR = VP - V0;
if (Kross(edgeR, edgeL) > 0) {
// vertex is convex
return (Kross(diff, edgeR) > 0 and Kross(diff, edgeL) < 0);
} else {
// vertex is reflex
return (Kross(diff, edgeR)<0orKross(diff, edgeL) > 0);
}
}
Two facts about diagonals and ears are presented in Meister (1975). The first fact
is that a polygon with at least four vertices has at least one diagonal. The second fact,
referred to as Meister’s Two Ears Theorem, is that a polygon with at least four vertices
must have at least two nonoverlapping ears.
13.9.2 Triangulation
Let a simple polygon have vertices V
i
for 0 ≤ i<n.Atriangulation of the polygon is
a partition of the polygon into triangles. Each triangle has vertices from the original
polygon. If two triangles in the partition intersect, they may only do so at vertices
or edges, not at interior points. Triangle edges that are introduced by the process are
necessarily inside the polygon, so those edges must be diagonals. All of the diagonals
used in the triangulation must be pairwise nonintersecting, by definition. It turns out
that any triangulation of the polygon must use n − 3 diagonals and contains n − 2
triangles.
It is possible to have a smaller number of triangles whose union is the original
polygon, but in this case T-junctions must occur. Equivalently this means that non-
diagonal segments must be used to connect vertices. For example, the polygon with
772 Chapter 13 Computational Geometry Topics
ordered vertices V
0
= (0, 0), V
1
= (1, −1), V
2
= (1, 1), V
3
= (−1, 1), V
4
= (−1, −1)
can be partitioned into three triangles, the index triples being {0, 1, 2}, {0, 2, 3}, and
{0, 3, 4}. The diagonals used in the triangulation are {0, 2}and {0, 3}. A partition with
only two triangles is {0, 1, 2} and {2, 3, 4}, but V
0
is a T-junction and the segment
{2, 4}is not a diagonal. T-junctions are usually not desirable in applications.
Triangulation by Ear Clipping
Because triangulation of a polygon involves the diagonals of the polygon, a divide-
and-conquer algorithm may be used to construct the triangulation. The idea is to find
a diagonal, split the polygon along the diagonal into two subpolygons, and recurse on
each subpolygon. The pseudocode is shown below where the top-level call passes in
a polygon stored as a linked list and an empty list of index triples. It is assumed that
the polygon has at least three vertices.
void Triangulate(VertexList vlist, TriangleList tlist)
{
n = vlist.size;
if (n == 3) {
tlist.Add(vlist(0), vlist(1), vlist(2));
return;
}
for (i0 = 0; i0 < n; i0++) {
for (i1 = 0; i1 < n; i1++) {
if (IsDiagonal(vlist, i0, i1)) {
Split(vlist,sublist0, sublist1);
Triangulate(sublist0, tlist);
Triangulate(sublist1, tlist);
return;
}
}
}
}
The double loop is O(n
2
) and the diagonal test is O(n), so finding a diagonal
in this way is O(n
3
). Using linked lists, the split operation is O(1). Therefore, it
takes O(n
3
) time before triangulation of the subpolygons. As a coarse analysis, if the
subpolygonseachhaveaboutn/2 vertices, then the recurrence formula for the time
T
n
it takes to solve the original problem is T
n
= 2T
n/2
+ O(n
3
). Applying the master
theorem in Cormen, Leiserson, and Rivest (1990) yields T
n
= O(n
3
).
A variation that is slightly simpler to analyze uses ear clipping. Rather than search
for any diagonal, it suffices to find an ear, add the corresponding triangle to the
13.9 Polygon Partitioning 773
list, remove the ear from the polygon, and recurse on the reduced polygon. The
pseudocode is
void Triangulate(VertexList vlist, TriangleList tlist)
{
n = vlist.size;
if (n == 3) {
tlist.Add(vlist(0), vlist(1), vlist(2));
return;
}
for(i0=0,i1=1,i2=2,i0<n;
i0++, i1 = (i1 + 1) mod n, i2 = (i2 + 1) mod n) {
if (IsDiagonal(vlist, i0, i2)) {
RemoveVertex(vlist, i1, sublist);
Triangulate(sublist, tlist);
return;
}
}
}
In this case, the outer loop and diagonal search combined are O(n
2
).Thevertex
removal is O(1). The subpolygon has n −1 vertices, so the recurrence formula for the
execution time is T
n
= T
n−1
+ O(n
2
). The solution to this recurrence is T
n
= O(n
3
),
the same order as the previous method.
The ear clipping algorithm can be further modified so that it is, in fact, an O(n
2
)
algorithm. The idea is to make an initial pass over the polygon and keep track of
which vertices are ear tips and which are not. The number of vertices to process is
n and each ear test is O(n), combined to yield O(n
2
). A second pass removes an ear,
say, with ear tip located at vertex i. The earness, so to speak, of vertices i − 1 and i +1
can change because of the removal. The earness of the other vertices does not change.
Therefore, each ear removal requires only two updates to determine if the vertices
i −1 and i + 1 are ear tips for the reduced polygon. Each update involves a diagonal
test, an O(n) operation. The second pass is effectively an iteration over O(n) ears,
each update requiring O(n) time for diagonal testing, so the combined pass is also
O(n
2
). The pseudocode is
void Triangulate(VertexList vlist, TriangleList tlist)
{
// dynamic list for polygon, to be reduced as ears are clipped
VertexList vdynalist = vlist.Copy(); // copy entire list
int vdynaquantity = vlist.Size();
