Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

101
;
zyx
x
cos
2
1
2
1
2
1
1
++
=α
;
zyx
y
cos
2
1
2
1
2
1
1
++
=β
.
zyx
z
cos
2
1
2
1
2
1
1
++
=γ
Для напрямних косинусів справедлива рівність
1coscoscos
222
=γ+β+α .(Це випливає з (2.9))
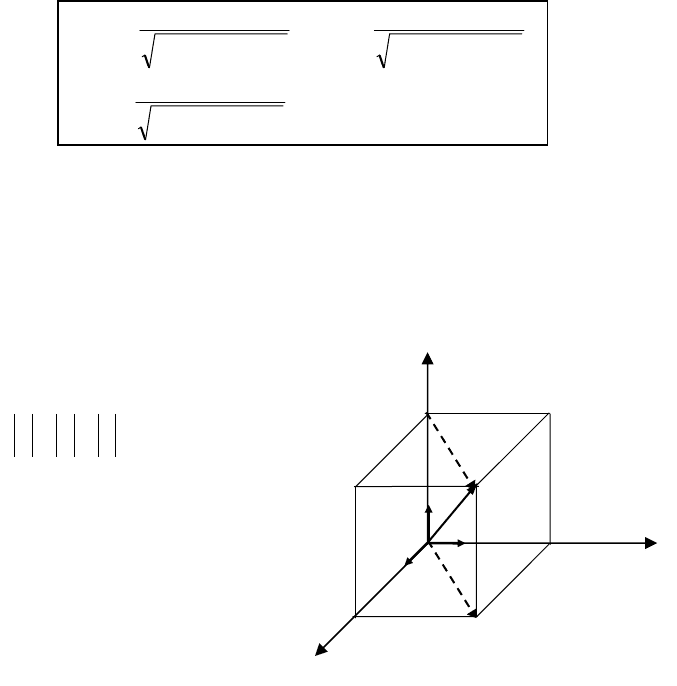
§9. Розклад вектора по ортам
Розглянемо прямокутну систему координат в просторі і век-
тор, початок якого в точці
O (мал.19).Позначимо орти осей коорди-
нат
Oz,Oy,Ox відповідно
через
→→→
k,j,i
, причому
.1kji ===
→→→
Спроектуємо вектор
→
OM на координатні осі (че-
рез точку
M
проведемо
площини, перпендикулярні
до координатних осей). Про-
екціями точки
M
на коорди-
натні осі будуть відповідно
точки
А,В,С (мал.19).
З прямокутника
ODMC видно, що вектор
→→→
+= OCODOM ,
але з прямокутника
AOBD одержуємо, що вектор
.OBOAOD
→→→
+= Тоді
→→→→
++= OCOBOAOM (2.10)
Вектор
→
OM , який сполучає точку O з точкою M(x,y,z) нази-
вається радіусом-вектором цієї точки.
Вектори
→→→
OC,OB,OA називаються складовими або
→
k
→
j
→
і
→
r
M
C
В
А
О
у
z
х
Мал.19.
D
(2.9)
102
компонентами вектора
→
OM , а їх величини
zOC,yOB,xOA ===
координатами цього вектора. Компоненти вектора
→
OM виразимо
через його координати і одиничні вектори
→→→
k,j,i , а саме
,ixOA
→→
= ,jyOB
→→
= .kzOC
→→
=
Підставляючи ці значення в рівність (2.10), враховуючи, що
→→
= rOM , одержимо
→→→→
++= kzjyixr (2.11)
Доданки
→→→
kz,jy,ix є складовими або компонентами вектора
→
r
.
Трійка векторів
→→→
k,j,i
називається координатним базисом, а
розклад (2.11) називається розкладом вектора по базису
→→→
k,j,i
. Це
основна формула векторної ал-
гебри.
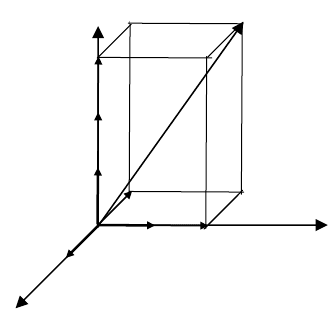
Приклад 1. Побудувати век-
тор
).3;2;1(r −=
→
Розв
’язування. Компоненти
вектора
→→→→→
=−= j2OB,iOAr є
і
→→
= k3OC і їм відповідає пря-
мокутний паралелепіпед, діаго-
наль якого є шуканий вектор
(мал.20).
§10. Дії над векторами, заданими в координатній формі
Якщо вектори задані в координатній формі, то дії додавання,
віднімання, множення вектора на число можна замінити простими
арифметичними операціями над координатами цих векторів за та-
кими правилами.
Правило 1. При
додаванні векторів їх однойменні координати
додаються.
→
r
у
→
k
→
j
→
і
M
C
В
А
О
z
х
Мал.20.
N
D

103
Нехай маємо вектори )z;y;x(a
111
→
і )z;y;x(b
222
→
.
Знайдемо
→→→
+= bac . Запишемо розклади векторів
→→
bіa по ор-
тах. Тоді
→→→→
++= kzjyixa
111
,
→→→→
++= kzjyixb
222
. Додавши ці
рівності, одержимо
→→→→
+++++= k)zz(j)yy(i)xx(c
212121
.
Отже, координати вектора
→
c будуть
).zz;yy;xx(c
212121
+++=
→
Правило 2. Щоб відняти від вектора
)z;y;x(a
111
→
вектор
)z;y;x(b
222
→
потрібно відняти від координат вектора
→
a
відповідні
координати вектора
→
b , тобто
).zz;yy;xx(bac
212121
++−=−=
→→→
Правило 3. Щоб помножити вектор
→
a на число λ , потрібно
кожну з його координат помножити на це число. Тобто , якщо
→→→→
++= kzjyixa
111
, то
→→→→
λ+λ+λ=λ kzjyixa
111
.
Приклад 1. Знайти вектор
→→→→
−+= b2)ba(3c , якщо
)5;2;1(a
→
= , ).4;3;2(b −
→
Розв
’язування. Виконаємо дії послідовно і знайдемо
).9;1;3()4;3;2()5;2;1(ba −=−+=+
→→
)27;3;9()9;1;3(3)ba(3 −=−=+
→→
, )8;6;4()4;3;2(2b2 −=−=
→
Значить,
).19;3;5()8;6;4()27;3;9(b2)ba(3c =−−−=−+=
→→→→
§11. Скалярний добуток двох векторів
Означення. Скалярним добутком двох векторів
називається число, яке дорівнює добутку їх довжин (модулів) на
косинус кута між ними.
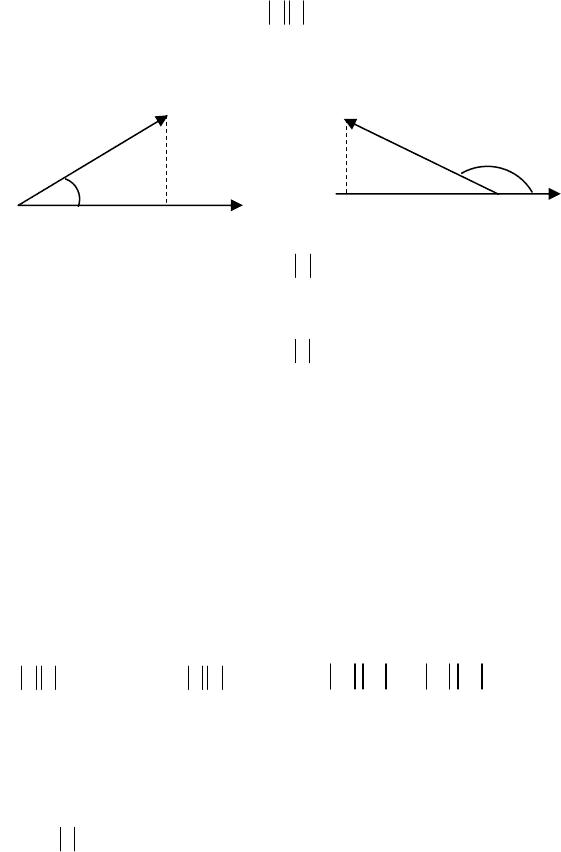
104
Скалярний добуток векторів
→→
bіa позначається символом
→→
⋅ ba . За означенням
ϕ=⋅
→→→→
cosbaba , (2.12)
де
ϕ
- кут між векторами
→→
bіa (мал.21), причому
π≤
ϕ
≤0
На основі формули (2.7) формулу (2.12) можна записати так:
→→→→
→
=⋅ bПрaba
a
(2.13)
або аналогічно
→→→→
→
=⋅ aПрbba
b
(2.14)
Отже, скалярний добуток двох векторів дорівнює добутку мо-
дуля одного з них на проекцію другого вектора на напрям першого.
Поняття скалярного добутку випливає із задач механіки.
Відомо, що робота
A сили F при прямолінійному переміщенні
матеріальної точки на шляху
l знаходять за формулою
)l,Fcos(lFA
∧
⋅=
(2.15)
Розглянемо деякі властивості скалярного добутку:
1)
→→→→
⋅=⋅ abba
- переставний закон.
Доведення
. За означенням скалярного добутку
ϕ=⋅
→→→→
cosbaba і ,cosabab ϕ=⋅
→→→→
але
→→→→
= abba
як добуток
чисел, то
→→→→
⋅=⋅ abba .
2)
→→→→
⋅λ=⋅λ
`
b)a()ba(
- сполучний закон.
Доведення
. На основі формули (2.14) маємо, що
),a(Прbb)a(
b
→→→→
λ=⋅λ
→
Мал
.21.
О
А
→
а
→
в
φ
а)
А
φ
→
а
→
в
б)
105
Таким чином,
Згідно з властивостями проекцій §6
→→
→→
λ=λ aПр)a(Пр
bb
.
Таким чином,
.aПрbaПрb)a(Прbb)a(
bbb
→→→→→→→→
→→→
λ=λ=λ=⋅λ
З другого боку, на основі формули (2.14), маємо
→→→→
⋅=
→
baaПрb
b
.
Отже,
)ba()a(Прb(b)a(
b
→→→→→→
⋅λ=λλ=⋅λ
→
.
3)
→→→→→→→
⋅+⋅=+ caba)cb(a
- розподільний закон.
Доведення
. На основі формули (2.14) маємо
),cb(Прa)cb(a
a
→→→→→→
+=+
→
Згідно з властивостями проекцій
→→→→
→→→
+=+ сПрbПр)cb(Пр
aaa
.сПрabПрa)cПрbПр(a)cb(Прa)cb(a
aaaaa
→→→→→→→→→→→→→
→→→→→
+=+=+=+
На основі формули (2.14) маємо, що
→→→→
⋅=
→
bаbПрa
a
і
→→→→
⋅=
→
сасПрa
a
Значить
.cabaсПрabПрa)cb(a
aa
→→→→→→→→→→→
⋅+⋅=+=+
→→
4)
2
aaa
→→→
=⋅ .
Доведення
. За означенням скалярного добутку
2
a0cosaaaa
→→→→→
==⋅ , якщо .0a ≠
→
Якщо
0a =
→
,то добуток 0aa =⋅
→→
, але тут 0a =
→
і рівність
2
aaa
→→→
=⋅ також правильна.
Скалярний добуток
→→
⋅ aa називають скалярним квадратом век-
тора
→
a
, тобто
22
aaaa
→→→→
==⋅
і звідси
.aa
2
→→
=

106
5) 0ba =⋅
→→
, якщо
→→
⊥ ba і навпаки, якщо
→→
⊥ ba , то 0ba =⋅
→→
.
Доведення
. За означенням скалярного добутку
.cosbaba ϕ=⋅
→→→→
Якщо
2
π
=ϕ
, то вектори
→→
bіa перпендикулярні,
0cos =
ϕ
і
0ba =⋅
→→
.Якщо
0ba =⋅
→→
, але
0ba ≠
→→
, то 0cos =
ϕ
,
2
π
=ϕ
,
тобто вектори
→
a і
→
b перпендикулярні.
◙ Скалярний добуток векторів в координатній формі.
Тому що одиничні вектори (орти)
→→→
k,j,i осей Oz,Oy,Ox
прямокутної системи координат взаємно перпендикулярні, то на
основі п’ятої властивості скалярного добутку, маємо
,0ijji =⋅=⋅
→→→→
,0jkkj =⋅=⋅
→→→→
.0ikki =⋅=⋅
→→→→
(2.16)
Крім цього, за четвертою властивістю скалярного добутку
,1ii =⋅
→→
,1jj =⋅
→→
.1kk =⋅
→→
(2.17)
Нехай задано два вектори з своїми координатами
),z;y;x(a
111
=
→
).z;y;x(b
222
=
→
Запишемо розклади цих векторів по ортам (формули 2.11)
,kzjyixa
111
→→→→
++= .kzjyixb
222
→→→→
++=
Знайдемо скалярний добуток цих векторів
)kzjyix)(kzjyix(ba
222111
→→→→→→→→
++++= .
Використовуючи формули (2.16), (2.17) знаходимо
212121
zzyyxxba ++=
→→
(2.18)
Таким чином, скалярний добуток двох векторів дорівнює сумі
добутків однойменних координат цих векторів.
Якщо
,ba
→→
= то ,xx
21
=
21
yy = , .zz
21
= При цьому
отримаємо на основі рівності (2.18), що
,zyxa
2
1
2
1
2
1
2
++=
→
або
2
1
2
1
2
1
zyxa ++=
→
(2.19)
Довжина вектора дорівнює квадратному кореню із суми
квадратів його координат.

107
.
3
16
212
221424
b
ba
a
Пр
222
b
=
++
⋅+⋅+⋅
=
⋅
=
→
→→
→
→
Із формули (2.12) знаходимо кут між двома векторами
→→
→→
⋅
=ϕ
ba
ba
cos
(2.20)
Формулу (2.20) на основі формул (2.18) і (2.19) запишемо у
вигляді
2
2
2
2
2
2
2
1
2
1
2
1
212121
zyxzyx
zzyyxx
cos
++⋅++
++
=ϕ
(2.21)
Якщо вектори
→
a і
→
b є колінеарні, то вони задовольняють
умові (2.6) , а саме
→→
λ= ab (2.22)
де скалярний множник
0>λ , коли вектори
→
b і
→
a мають одинако-
вий напрям, і
λ<0 якщо протилежні напрями. Рівність (2.22) в
координатній формі запишеться так:
12
xx λ= ,
12
yy λ= ,
12
zz λ= або
λ===
1
2
1
2
1
2
z
z
y
y
x
x
(2.23)
Умова (2.23) є умовою паралельності векторів
→
a і
→
b .Отже,
якщо вектори
→
a і
→
b колінеарні, то їх однойменні координати
пропорціональні і навпаки.
Необхідною і достатньою умовою перпендикулярності
векторів
→
a і
→
b є рівність 0ba =
→→
або в координатній формі
0zzyyxx
212121
=++
(2.24)
Умова (2.24) є умовою перпендикулярності двох векторів.
Приклад 1.Знайти проекцію вектора
)2;4;4(a =
→
на напрям
вектора
).2;1;2(b =
→
Розв’язування. Із формули (2.14) одержимо
Приклад 2. Виразити через орти
→→→
k,j,i орт
→
a вектора
)6;2;3(a −=
→
.

108
Розв’язування. Одиничний вектор
.k
7
6
j
7
2
i
7
3
6)2(3
k6j2i3
a
a
a
222
→→→
→→→
→
→
→
+−=
+−+
+−
==
Приклад 3. Підприємство випускає продукцію чотирьо видів
в кількості 210, 160, 172 і 300 штук. Ціни в одних і тих же грошових
одиницях задані в такому порядку: 4,3;1,2;7;2,1. Обчислити сумарну
ціну всієї продукції.
Розв
’язування. Запишимо дані про випуск продукції у вигляді
векторів
)300;172;160;210(а =
→
, а також ціни одиниці кожної із
виду продукції
)1,2;0,7;2,1;3,4(b =
→
.Тепер сумарна ціна П всієї
продукції запишеться на основі формули 2.18.
29291,23000,71722,11603,4210baП =⋅+⋅+⋅+⋅==
→→
.
§12. n-мірний вектор і векторний простір
Множина всіх векторів, які ми розглядали на площині або в
просторі і для яких визначені операції додавання векторів, множен-
ня вектора на число є простими прикладами векторного простору.
Означення 1. Упорядкована множина n дійсних чисел, за-
писаних у вигляді
)a,...,a,a,a(
n321
називається n- мірним векто-
ром. Числа
n321
a,...,a,a,a називаються координатами вектора
→
a , тобто )a,...,a,a,a(a
n321
=
→
.
Поняття n-мірного вектора широко використовується в
економіці, наприклад, деякий набір товарів можна охарактеризувати
вектором )a,...,a,a,a(a
n321
=
→
, а відповідно ціни вектором
).b,...,b,b,b(b
n321
=
→
Якщо в
n-мірного вектора одна координата дорівнює одиниці,
а всі решту рівні нулю, то такий вектор називається одиничним.
Очевидно, що існує
n різних одиничних векторів
),0,...,0,0,1(e
1
=
→
),...0,...,0,1,0(e
2
=
→
),1,...,0,0,0(e
n
=
→
які виходять із початку координат точки
О. Всі означення і дії для
109
двомірних і тримірних векторів, заданих в координатній формі, роз-
повсюджуються і на
n-мірні вектори (n≥4).
Два
n-мірні вектори рівні тоді і тільки тоді, коли їх відповідні
компоненти рівні.
Вектор )a,...,a,a,a(a
n321
=
→
і вектор )b,...,b,b,b(b
n321
=
→
рівні, коли
a
i
=b
i
( ).n,...,3,2,1i =
Сумою двох n-мірних векторів
→
a і
→
b є третій n-мірний вектор
→
с , координати якого дорівнюють сумі відповідних однойменних
координат векторів
→
a
і
→
b
, тобто
iii
baс += ( ).n,...,3,2,1i =
Добутком вектора
→
a
на дійсне число λ називається вектор
→→
λ= ad , координати якого
i
d дорівнюють добутку числа λ на
відповідні координати вектора
→
a , тобто
ii
ad λ= ( ).n,...,3,2,1i =
Вектор, у якого всі координати дорівнюють нулю, називається
нульовим вектором і позначається
).0,...,0,0(0 =
→
Операції над довільними векторами задовольняють влас-
тивостям:
1.
→→→→
+=+ abba
- переставний закон;
2.
−++=++
→→→→→→
)cb(aс)ba( сполучний закон;
3.
→→
αβ=βα a)()a( - сполучний закон, відносно числового
множника;
4.
λ (
→→→→
λ+λ=+ ba)ba - розподільчий закон відносно суми
векторів;
5.
→→→
β+α=β+α aaa)(
- розподільчий закон відносно суми
числових множників.
6. Існує нульовий вектор
),0,...,0,0(0 =
→
такий,що
→→→
=+ a0a
для довільного вектора
→
a ;

110
7. Для довільного вектора
→
a існує протилежний вектор (-
→
a ),
такий, що
→→→
=−+ .0)a(a
8.
→→
=⋅ aa1 , для довільного вектора
→
a (особлива роль число-
вого множника 1).
Означення. Множина векторів з дійсними координатами, в
якій визначено операції додавання векторів і множення вектора
на число, які задовольняють вище приведеним восьми властиво-
стям називається векторним простором.
Зауваження. Якщо під векторами
→→→
сіb,a
можна розглядати
елементи довільної природи, то відповідна множина елементів
називається лінійним простором.
Лінійним простором є, наприклад, множина всіх алгебраїчних
многочленів степені яких не перевищують натурального числа
n
.
Якщо множина всіх многочленів точно дорівнює натуральному чис-
лу
n, то не буде лінійним простором тому, що сума двох
многочленів може виявитися многочленом, степінь якого менше
n.
§13. Базис. Розклад вектора по даному базису
Введемо поняття лінійної комбінації, лінійної залежності, а
також базису і розклад вектора по базису.
Означення 1. Вектор
→
b називається лінійною комбінацією
векторів
→→→
m
21
a,...,a,a векторного простору
,R
m
якщо він дорівнює
сумі добутків цих векторів на довільні дійсні числа
→→→
+++=
mm2
1
1
ak...akakb
2
(2.25)
де
m21
k,...,k,k - дійсні числа.
Означення 2. Вектори
→→→
m
21
a,...,a,a називаються лінійно
залежними, якщо існують такі числа
m21
k,...,k,k , які не
дорівнюють одночасно нулю, що
0ak...akak
mm2
1
1
2
=+++
→→→
(2.26)
