Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

81
;7,15715771,0xax
31313
=⋅== ;1,828211,0xax
12121
=⋅==
;4,28014022,0xax
22222
=⋅== ;5,78815775,0xax
32323
=⋅==
;1,828211,0xax
13131
=⋅== ;6,42014023,0xax
23232
=⋅==
.2,94615776,0xax
33333
=⋅==
Різниця між матрицею повних витрат
1
B
−
і матрицею прямих
витрат
A
визначає матрицю непрямих (посередницьких) витрат
C
:
.
21,979,467,3
8,765,568,1
24,453,201,3
6,03,01,0
5,02,04,0
1,03,02,0
81,909,577,3
3,885,508,2
34,483,221,3
ABC
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=−=
−
Таким чином, елементи
ij
с матриці C і є коефіцієнтами не-
прямих (посередницьких) витрат.
Задача 2. (задача знаходження витрат сировини, палива та
трудових ресурсів.) Використовуючи вихідні дані і результати об-
числень попередньої задачі 1, потрібно знайти:
1. Сумарні витрати сировини, палива і трудових ресурсів для
виконання програми виробництва.
2. Коефіцієнти прямих витрат сировини, палива та праці на
одиницю продукції
кожної галузі.
3. Повні витрати сировини, палива і праці окремими галузями
і господарством в цілому.
4. Внутрівиробничі витрати галузей.
5. Внутрівиробничі витрати на кожну одиницю товарної
продукції.
При цьому відомі витратні норми сировини і палива на виро-
бництво одиниці продукції кожної галузі, трудомісткість в людино-
годинах на одиницю продукції, їх
вартість і представлені таблицею:
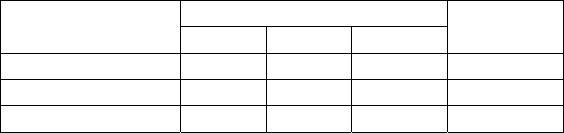
Показники
Норми витрат цехів Вартість
1 2 3
Сировина 0,8 1 1,2 6
Паливо 3 1,5 2 4
Трудомісткість 8 5 5 1,5
82
Розв
’язування. Запишемо матрицю
D
, складену із норм ви-
трат сировини, палива та праці, а також матрицю-рядок
P
вартос-
тей цих показників.
,
558
25,13
2,118,0
D
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
[]
.5,146P =
Запишемо також результати обчислень попередньої задачі:
,
1577
1402
821
X
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
−
81,909,577,3
3,885,508,2
34,483,221,3
B
1
,
де
X
- матриця-стовпець плану валового випуску продукції;
1
B
−
- матриця коефіцієнтів повних витрат.
1) Перемноживши матрицю
D
норм витрат сировини, палива
та праці і матрицю-стовпець плану валового випуску продукції
X
,
одержимо матрицю-стовпець сумарних витрат сировини, палива і
трудових ресурсів:
≈
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅+⋅+⋅
⋅+⋅+⋅
⋅+⋅+⋅
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=⋅
15775140258218
1577214025,18213
15772,1140218218,0
1577
1402
821
558
25,13
2,118,0
XD
.
21463
7720
3951
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
≈
Отже, для виконання програми виробництва потрібно витра-
тити 3951 одиниць сировини, 7720 одиниць палива і 21463 робочих
людино-годин.
2) Добуток матриці
D
норм витрат сировини, палива та праці
і матриці коефіцієнтів повних витрат
1
B
−
визначає матрицю
коефіцієнтів прямих витрат сировини, палива та праці на одиницю
продукції кожної галузі:
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=⋅=
−
81,909,577,3
3,885,508,2
34,483,221,3
558
25,13
2,118,0
BDV
1
83
.
27,12534,7793,54
09,4545,2729,20
54,2322,1417,9
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
Тут елементи першого стовпця означають кількість витрат си-
ровини, другого – палива і третього – робочих людино-годин, які
потрібні для виготовлення одиниці продукції 1-ї, 2-ї і 3-ї галузей.
3) Добутки матриць-стовпців норм витрат сировини, палива та
праці і планового випуску продукції виражають витрати сировини,
палива та праці кожного із трьох галузей
:
;
6568
2463
8,656
821
8
3
8,0
П
1
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
= ;
7010
2103
1402
1402
5
5,1
1
П
2
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=⋅
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
.
7885
3154
4,1892
1577
5
2
2,1
П
3
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=⋅
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=
Таким чином, матриця повних витрат сировини, палива та
праці по трьох галузях має вигляд:
.
788570106568
315421032463
4,189214028,656
П
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
=
4) Перемноживши матрицю-рядок вартостей сировини, палива
та праці на матрицю повних витрат цих показників одержимо мат-
рицю-рядок вартостей витрат кожної із трьох галузей:
[] [ ]
.9,357972733914778
788570106568
315421032463
4,189214028,656
5,146ПP =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅=⋅
Це означає, що вартість витрат першої галузі становить 14778 оди-
ниць, другої – 27339 і третьої – 35797,9.
5) Добуток матриці-рядка вартостей
P
на матрицю прямих
витрат
V сировини, палива та праці дає внутрівиробничі витрати на
кожну одиницю товарної продукції:
[] [ ]
.51,50913,31158,218
27,12534,7793,54
09,4545,2729,20
54,2322,1417,9
5,146VP =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅=⋅
84
Задача 3. Для виготовлення дитячих іграшок використову-
ються відходи полотняних матеріалів
)М,М,М(
321
різних розмі-
рів. Обчислити кількість матеріалу, який витрачається при розкрої
трьома способами, якщо кількість заготовок одержаних з кожного
матеріалу, а також кількість необхідних заготовок представлена
таблицею:
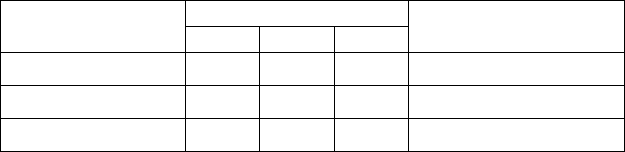
Вид заготовки
Спосіб розкрою
Кількість заготовок
1 2 3
1
М
1 2 3 126
2
M
2 3 3 134
3
M
4 3 3 189
Розв’язування. Якщо
321
x,x,x
- кількість вихідного матеріалу
)М,М,М(
321
, який використовується для розкрою відповідно пе-
ршим, другим і третім способами, то для виконання поставленої ме-
ти, потрібно розв'язати систему лінійних рівнянь:
⎪
⎩
⎪
⎨
⎧
=++
=++
=++
.189x3x3x4
,134x2x3x2
,126x3x2x
321
321
321
Розв’яжемо її методом Гаусса. Виключимо невідому величину
1
x із другого і третього рівнянь. Для цього помножимо перше
рівняння на “-2”, “-4” і додамо відповідно до другого і третього рів-
нянь:
⎪
⎩
⎪
⎨
⎧
−=−−
=+
=++
.315x9x5
,118x4x
,126x3x2x
32
32
321
Виключимо невідому
2
x
із третього рівняння. При цьому по-
множимо друге рівняння на “5” і додамо до третього рівняння:
⎪
⎩
⎪
⎨
⎧
=
=+
=++
.275x11
,118x4x
,126x3x2x
3
32
321
Звідси, розв’язок системи лінійних рівнянь буде
х
1
=15; х
2
=18;
х
3
=25. Отже, при певних методах розкрою матеріалу, потрібно мати
15 шт. матеріалу
М
1
, 18 шт. матеріалу М
2
і 25 шт. матеріалу М
3
85
Задача 4. Для виготовлення чотирьох видів продукції P
1
, P
2
,
P
3
,P
4
використовуються три види сировини S
1
, S
2
, S
3
. Норми витрат і
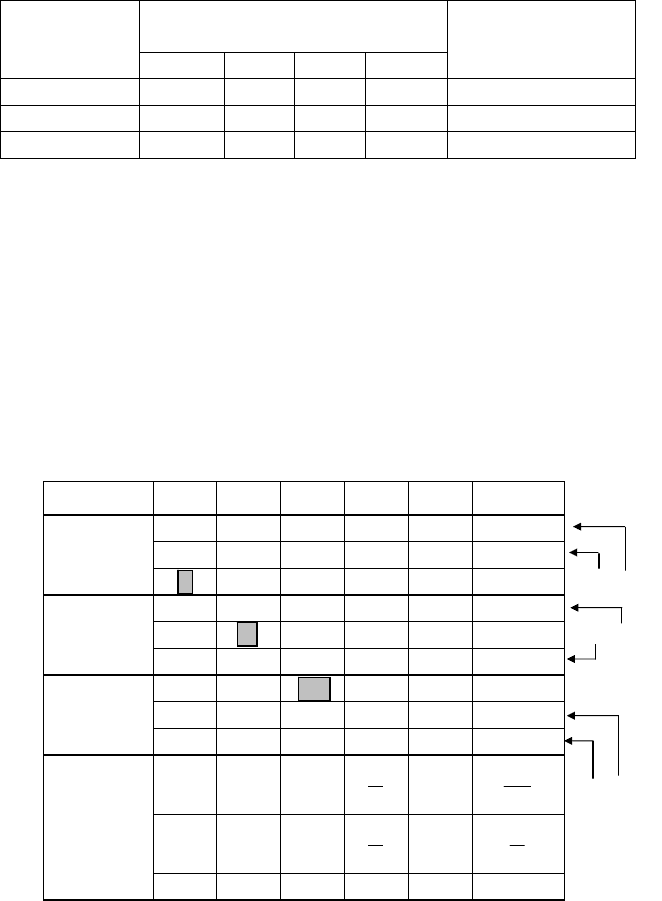
запаси сировини наведені в таблиці:
Сировина Витрати сировини на одини-
цю продукції
Запаси сировини
P
1
P
2
P
3
P
4
S
1
3 2 2 1 14
S
2
2 5 2 3 15
S
3
1 2 2 3 10
Визначити кількість продукції P
1
, P
2
, P
3
, P
4
, якщо ресурси по-
вністю вичерпані.
Розв
’язування. Позначимо через x
1
, x
2
, x
3
, x
4
кількість одиниць
продукції
P
1
, P
2
, P
3
, P
4
. Умову нашої задачі можна записати у вигля-
ді системи лінійних рівнянь:
⎪
⎩
⎪
⎨
⎧
=+++
=+++
=+++
.10x3x2x2x
,15x3x2x5x2
,14xx2x2x3
4321
4321
4321
Розв’яжемо її методом Жордана-Гаусса в табличній формі. В
якості першої таблиці запишемо коефіцієнти, які стоять біля неві-
домих і стовпчик з вільних членів. Стовпець (
Σ ) є контрольним,
який представляє суму чисел відповідного рядка.
Таблиця
1
x
2
x
3
x
4
x
i
b
∑
1
3 2 2 1 14 22
2 5 2 3 15 27
1 2 2 3 10 18
2
0 -4 -4 -8 -16 -32
0 1 -2 -3 -5 -9
1 2 2 3 10 18
3
0 0 -12 -20 -36 -68
0 1 -2 -3 -5 -9
1 0 6 9 20 36
4
0 0 1
3
5
3
3
17
0 1 0
3
1
1
3
7
1 0 0 -1 2 2
×(-2),(-3)
×(-2),(4)
×(-6),(2)
×(-1/12)

86
Таблиця
1. За ключовий елемент взято число “1” в третьому
рядку і першому стовпці. Для утворення нулів в ключовому стовпці
на місці чисел “2”, “3”, помножимо елементи ключового рядка на
“-2” і “-3”, і додамо відповідно до елементів другого і першого ряд-
ків. Цим виключимо невідому
1
x в першому і другому рівняннях.
Таблиця
2. В якості ключового елемента візьмемо число “1”
(другий рядок і другий стовпець). Помножимо елементи другого
рядка на числа “4” і“-2” і додамо до елементів першого і третього
рядків. При цьому відбувся процес виключення невідомої
2
x
в
першому і третьому рівняннях.
Таблиця
3. За ключовий елемент візьмемо число “-12”.
Поділимо на нього всі елементи першого рядка. Запишемо одержані
числа елементами першого рядка наступної таблиці.
Таблиця
4. Помножимо елементи першого рядка на “-6” і “2”і
додамо до елементів третього і другого рядків таблиці 3.
Результати обчислень запишемо другим і третім рядком цієї
таблиці. Одержані нулі третього стовпця виражають виключення
невідомої
3
x із другого і третього рівнянь.
Останній таблиці відповідає система лінійних рівнянь
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=−
=+
=+
.2xx
,1x
3
1
x
,3x
3
5
x
41
42
43
Вона сумісна за теоремою Кронекера-Капеллі, оскільки ранг
основної і розширеної матриць рівні 3. Так як це число (3) менше,
ніж кількість невідомих (4), то система лінійних рівнянь має безліч
розв’язків. Невідомі
321
x,x,x є базисними, оскільки визначник
складений із коефіцієнтів, які стоять біля невідомих, відмінний від
нуля.
Тому
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
−=
−=
+=
.x
3
5
3x
,x
3
1
1x
,x2x
43
42
41

87
Оскільки
321
x,x,x
виражають кількість реалізованої
продукції, тому
.0x
i
≥ Значить
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≥−=
≥−=
≥+=
,0x
3
5
3x
,0x
3
1
1x
,0x2x
43
42
41
тобто
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
≤−≥−−≥−
≤−≥−
−≥
.
5
9
x,3x5,3x
3
5
,3x,1x
3
1
,2x
444
44
4
Із останньої системи випливає, що
5
9
x2
4
≤≤− .
Отже, довільному значенню
4
x
∈
⎥
⎦
⎤
⎢
⎣
⎡
−
5
9
;2 відповідає не-
від’ємний розв’язок , який задовольняє умову задачі. Наприклад,
для
.3x,1x,2x,0x
3214
====

88
Розділ 2. АНАЛІТИЧНА ГЕОМЕТРІЯ І ЕЛЕМЕНТИ
ВЕКТОРНОЇ АЛГЕБРИ
Аналітична геометрія є розділ математики, яка вивчає
властивості геометричних фігур алгебраїчними методами. Уже в
середній школі до геометрії застосовують алгебру при розв’язуванні
багатьох питань. Ще в
XYII
ст. французький математик Рене Де-
карт розробив метод координат, який є апаратом аналітичної
геометрії. Цей метод дає можливість визначити положення точки на
прямій, на площині, на поверхні, а форму ліній і поверхонь задати за
допомогою рівнянь, які пов’язують координати їх точок.
§1. Метод координат на прямій та його застосування
Розглянемо
горизонтальну пряму лінію l на площині (мал.1).
На цій прямій
l візьмемо нерухому
точку
O, що називається початком
відліку. Ця точка розбила пряму
на два взаємно протилежні на-
прямки: додатній – вправо і від’ємний – вліво. Взявши деяку одини-
цю масштабу, вправо від точки
Oвідкладаємо додатні числа, а вліво
– від’ємні числа. Ці числа відповідають деяким точкам на прямій
l і
навпаки, отже між точками прямої
l та дійсними числами існує
взаємно однозначна відповідність. Таку пряму
l будемо називати
числовою віссю
Ox. Точці O, що вважається початком відліку ,
відповідає число нуль.
Таким чином, ми побудували систему координат на прямій.
Візьмемо деяку точку
А на числовій осі. Цій точці відповідає деяке
число
х, яке називається координатою точки А. Це записується А(х).
Будемо вважати відрізок
1
ОА , що відкладений праворуч від
точки
O за додатній, а відрізок
2
ОА
відкладений ліворуч від точки
О- за від’ємний (мал.1).
Відрізок, у якого
A
початок, а В кінець, позначають
А
В
і на-
зивають напрямленим відрізком. Величину відрізка
AB
будемо
позначати символом
АВ.
Означення. Відрізки, які характеризуються не тільки своєю
довжиною, але й напрямом називаються напрямленими
відрізками.
l
А
2
А
1
О
Мал.1
89
Величина напрямленого відрізка є його довжина, взята з пев-
ним знаком.
Візьмемо на осі
x
-ів дві точки
1
A і
2
A відповідно з коорди-
натами
1
x і
2
x , тоді і відрізкам
1
ОА і
2
ОА будуть відповідати числа
1
x і
2
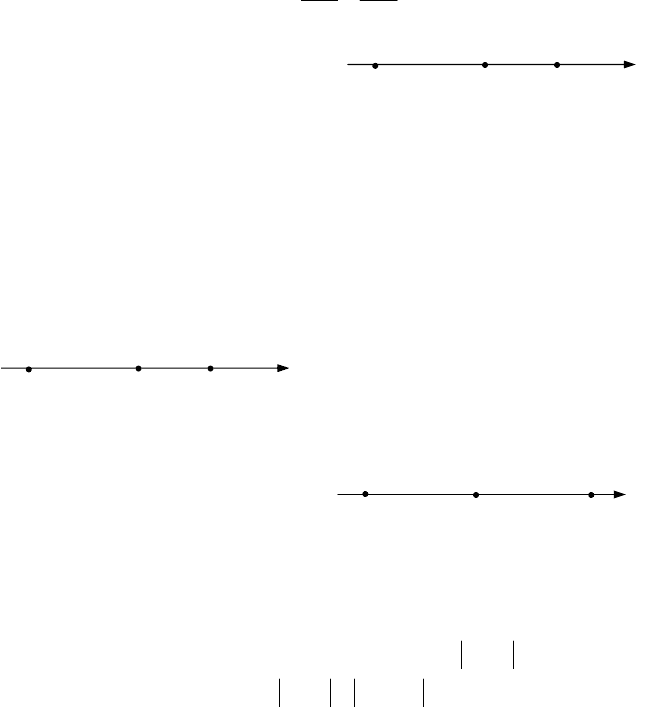
x (мал.2).
Покажемо, що при будь-
якому розташуванні точок
1
A і
2
A відносно точки
О
величина відрізка
21
AA буде
дорівнювати
,xx
12
−
тобто
1221
xxAA −= (2.1)
Дійсно, нехай точки
1
A і
2
A розташовані так як на мал.2.
Тоді
.xxОАОАAA
121221
−=−=
Коли точки
1
A і
2
A розташовані так, як на мал.3,
то
;ОАОААА
2121
−= але
11
ОАОА −=
і
22
ОАОА −=
Одержимо
.xx)ОА(ОААА
122121
−=−−−=
Нехай
1
A і
2
A розташовані
по різні сторони відносно точки
О (мал.4).
Значить
12122121
xxОАОАОАОААА −=−=+= .
Якщо
,3x
1
= а 5x
2
−= , то величина відрізка буде
.835АА
21
−=−−=
Довжина відрізка
21
АА позначається через
21
АА і дорівнює
1221
xxАА −= (2.2)
Висновок. Якщо на прямій в деякій системі координат задано
дві точки
)x(A
11
і )x(A
22
,тоді величина відрізка
21
AA знаходиться
із рівності (2.1), а віддаль (довжина) між цими точками за формулою
(2.2).
Приклад 1. Задано точки
),2(A),7(B − )3(C − .
Знайти величину відрізків
А
В ,
СВ
.
х
А
2
А
1
О
Мал.3
х
А
2
А
1
О
Мал
.2
А
2
х
А
1
О
Мал.4
А
2
90
Розв
’язування. За формулою (2.1) одержуємо:
927AB −=−−=
.
.437)3(7СВ −=+−=−−−=
Приклад 2. Знайти віддаль між точками
),3(A).7(B
Розв
’язування. За формулою (2.2) одержимо
.437АВd =−==
§2. Прямокутна система координат на площині
та її застосування
Положення точки на прямій, як ми бачили, визначається од-
ним числом – її координатою, а положення точки на площині, як ми
побачимо, визначається упорядкованою парою чисел (тобто вказано
яке із чисел є першим, а яке другим).
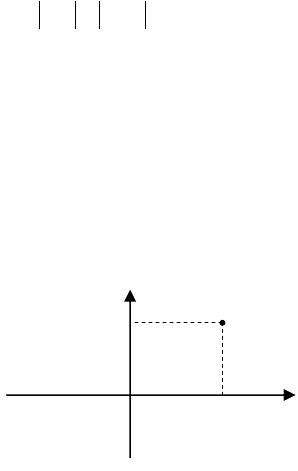
Візьмемо на площині дві взаємно перпендикулярні
осі і на-
звемо їх осями координат (мал.5).
Точка перетину осей координат
O
називається початком координат.
Осі координат (
Оx
- вісь абсцис,
горизонтальна,
−Oy
вісь ординат,
вертикальна ). Осі координат
Оx і
Oy ділять площину на чотири час-
тини, які називаються квадрантами
( або координатними кутами). Частина площини, що міститься між
додатними осями
Оx і Oy називається першим квадрантом.
Нумерація квадрантів іде проти годинникової стрілки.
Нехай точка
М
- довільна точка площини. Опустимо з цієї
точки перпендикуляри на вісь
Оx і Oy , основи цих
перпендикулярів позначимо відповідно через
1
М
і
1
N
, тобто
1
М і
1
N є проекціями точки
М
на координатні осі. Позначимо ко-
ординату точки
1
М на осі Ox через
,
x
а координату точки
1
N на
осі
Oy через
.
y
Числа )y,x( назвемо координатами точки
М
на
площині (
−
x
абсциса,
y
- ордината) . Це позначимо
М
)y,x(
.
Таким чином, система координат на площині встановлює
взаємно однозначну відповідність між множиною всіх точок
площини і множиною всіх упорядкованих пар дійсних чисел.
N
1
О
х
у
Мал.5
М
1
М
І
ІІ
ІІІ
І
V
