Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

91
◙ Найпростіші задачі на застосування методу координат.
а) Віддаль між двома точками на площині.
Нехай задані дві точки з
своїми координатами:
)y;x(A
11
,
)y;x(B
22
. Треба знайти віддаль
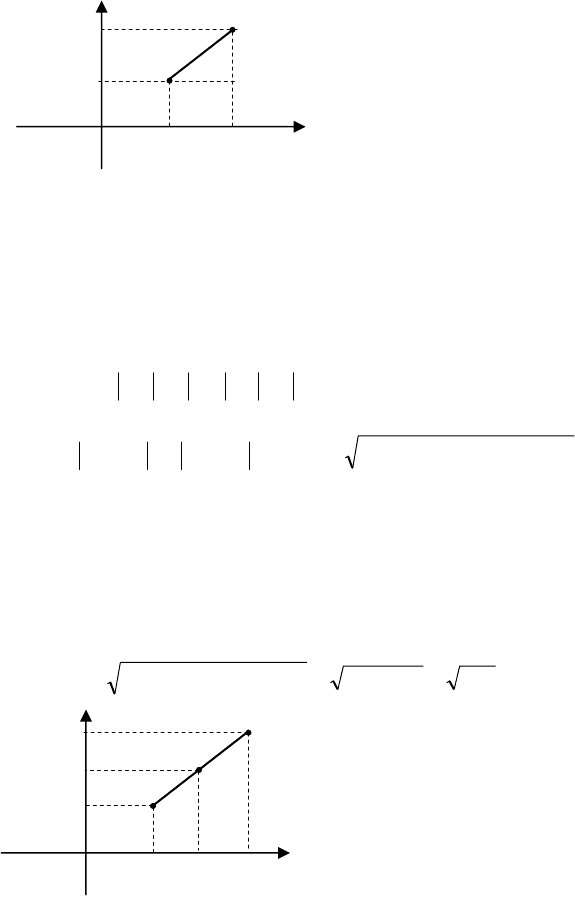
між цими точками. Зробимо малю-
нок (мал.6).
Точки
A
і
B
спроектуємо на
координатні осі. Їх проекції на
вісь
Ox позначимо відповідно через
1
A
і
1
B
, а на вісь
Oy
-
відповідно через
2
A і
2
B .
Тоді
,xОA
11
= ,xОB
21
= ,yОA
12
= .yОB
22
=
Через точку
A
проведемо пряму, паралельну осі абсцис до пе-
ретину з прямою
1
BB
в точці C . З одержаного прямокутного три-
кутника
ABC за теоремою Піфагора знаходимо
.BCACABd
222
2
+==
На основі формули (2.2) дану рівність перепишемо так:
2
12
2
12
2
yyxxd −+−= , або
2
12
2
12
)yy()xx(d −+−=
(2.3)
Знак перед коренем у формулі (2.3) береться (+) тому, що
віддаль – величина додатна.
Зауваження
. Різниця координат у формулі (2.3) підноситься
до квадрату і тому немає значення, яку точку вважати першою, а яку
другою.
Приклад . Знайти віддаль між точками
)5;4(A i )7;9(B − .
Розв
’язування. За формулою (2.3) знаходимо
.1316914425)57()49(d
22
==+=−−+−=
б
) Поділ відрізка в заданому
відношенні.
Нехай на площині задано дві
довільні точки
A(x
1
,y
1
) і B(x
2
,y
2
)
Вважаємо
A(x
1
,y
1
) першою точкою,
а
B(x
2
,y
2
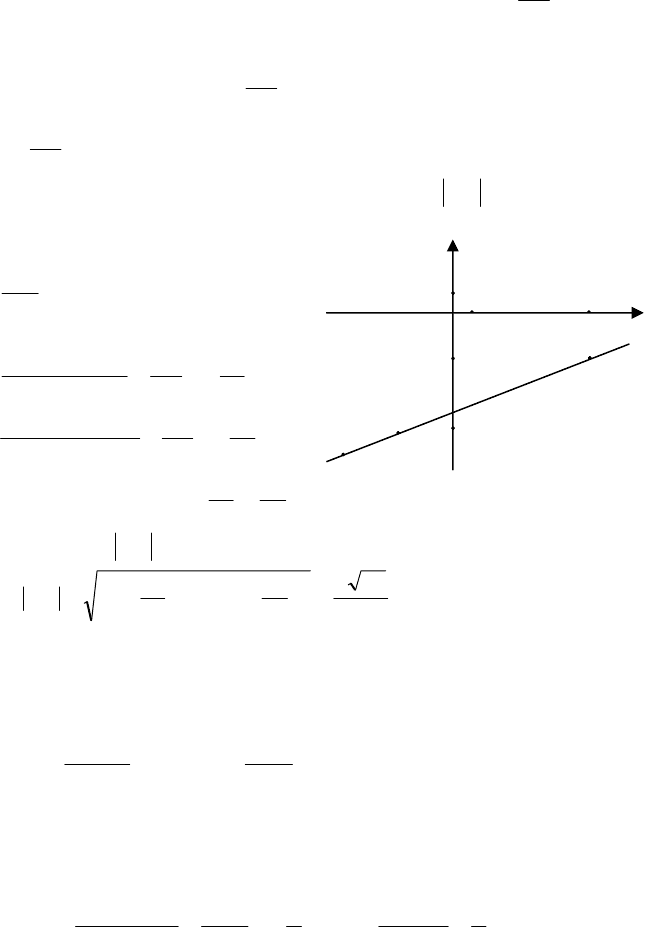
) другою точкою. Проведе-
мо через ці точки пряму(мал.7).
Нехай точка
)y,x(С лежить
d
B
B
2
A
2
О
х
у
Мал.6
A
1
A
B
1
C
B
1
C
1
C
2
C
B
B
2
A
2
О
х
у
Мал.7
A
1
A
х
1
х
2
х
y
y
1
y
2

92
на відрізку
AB
і ділить його на два відрізки AC і CB , причому
відношення їх дорівнює
λ , тобто
CB
AC
=λ
(число λ відоме). Випа-
док, коли точка
С співпадає з точкою
B
виключаємо, бо знаменник
перетворюється в нуль. Наша задача полягає в тому, щоб знайти ко-
ординати точки
)y,x(С
через координати точок
)y,x(A
11
,
).y,x(B
22
та число
λ
.
Спроектуємо точки
,A C та
B
на координатну вісь Ox (мал.7)
і позначимо їх проекції через
1
A ,
1
C та
1
B . Використовуючи тео-
рему про пропорційні відрізки, що містяться між паралельними
прямими, одержимо
.
CB
AC
BC
CA
11
11
λ== Відомо, що
,xxCA
111
−= ,xxBC
211
−=
тоді .
xx
xx
2
1
λ=
−
−
Розв’язуючи цю
рівність відносно
,
x
знаходимо .
1
xx
x
21
λ+
λ+
=
Аналогічно, спроектувавши точки
,A C та
B
на координатну
вісь
Oy
(мал.7) і зробивши необхідні викладки, як вище, знаходимо
ординату точки
C : .
1
yy
y
21
λ+
λ+
=
Отже, координати точки
)y,x(С , яка ділить відрізок
AB
у відношенні
λ
(рахуючи від
A
до
B
), обчислюються за форму-
лами
⎪
⎩
⎪
⎨
⎧
λ+
λ+
=
λ+
λ+
=
.
1
yy
y
,
1
xx
x
21
21
(2.4)
Якщо точка
C є серединою відрізка
AB
, то 1=λ і тоді
⎪
⎩
⎪
⎨
⎧
+
=
+
=
.
2
yy
y
,
2
xx
x
21
21
(2.5)
Зауваження
. При одержанні формул (2.4) ми допускали, що
відрізок
А
В
не паралельний ні одній з осей координат. Однак
93
одержані формули (2.4) справедливі і тоді , коли відрізок
А
В пара-
лельний вісі
Ox (
21
yyy ==
), або осі
Oy
(
)xxx
21
==
.
Крім цього, все викладене вище справедливе й тоді, коли точ-
ка
)y,x(С
знаходиться зовні
А
В
, тобто на його продовженні.
Приклад 1. Дано дві точки
A(7;-2)і B(-3;-5). На продовженні
прямої
А
В знайти точку C(x,y), віддаль від якої до точки A в п’ять
раз більша за віддаль до точки
B. Знайти довжину .AC
Розв
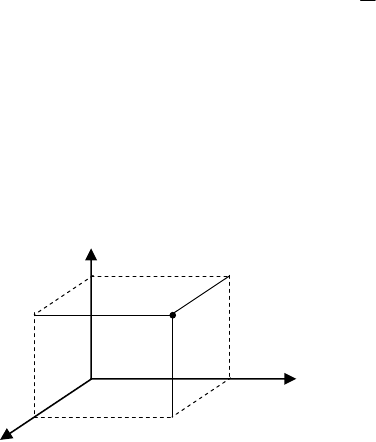
’язування. Зробимо малюнок.
За умовою задачі (мал.8)
.5
CB
AC
−==λ
Тепер за формулою
(2.4) знаходимо
,
2
11
4
22
)5(1
)3)(5(7
x −=
−
=
−+
−−+
=
.
4
23
4
23
)5(1
)5)(5(2
y −=
−
=
−+
−−+−
=
Значить, точка
)
4
23
;
2
11
(C −−
.
Довжину
АС знаходимо за формулою (2.3)
4
195
)
4
23
2()
2
11
7(
АС
22
=+−++=
.
Приклад 2. Знаючи координати вершин трикутника
)3;2(A , )5;4(B − і )5;2(C −− , знайти точку
M
перетину медіан
трикутника.
Розв
’язування. Координати точки
D
(середина сторони BC )
буде
3
2
24
x
D
−=
−−
= , 0
2
55
y
D
=
−
= ,тобто )0;3(D − .
Шукана точка
M
ділить кожну медіану у відношенні
1:2=λ , рахуючи від вершини. Тепер підставляючи у формули
(2.4)
2=λ
та координати точок
A
і
D
, знайдемо координати
шуканої точки
M
.
;
3
4
3
62
21
2)3(2
x
M
−=
−
=
+
⋅−+
= .1
3
3
21
203
y
M
==
+
⋅+
=
C
B
A
О
х
у
Мал.8
1
1
-3
-2
7
-5
94
Отже, ).1;
3
4
(M −
§3. Декартова прямокутна система координат в просторі
Положення точки в просторі будемо визначати відносно
прямокутної системи координат в просторі. Дана система
Оxyz
складається із трьох взаємно перпендикулярних осей
Oy,Ox
та
Oz , які перетинаються в одній точці O ,яка називається початком
координат. Вісь
Ox називається віссю абсцис, вісь Oy - віссю орди-
нат і вісь
Oz - віссю аплікат.
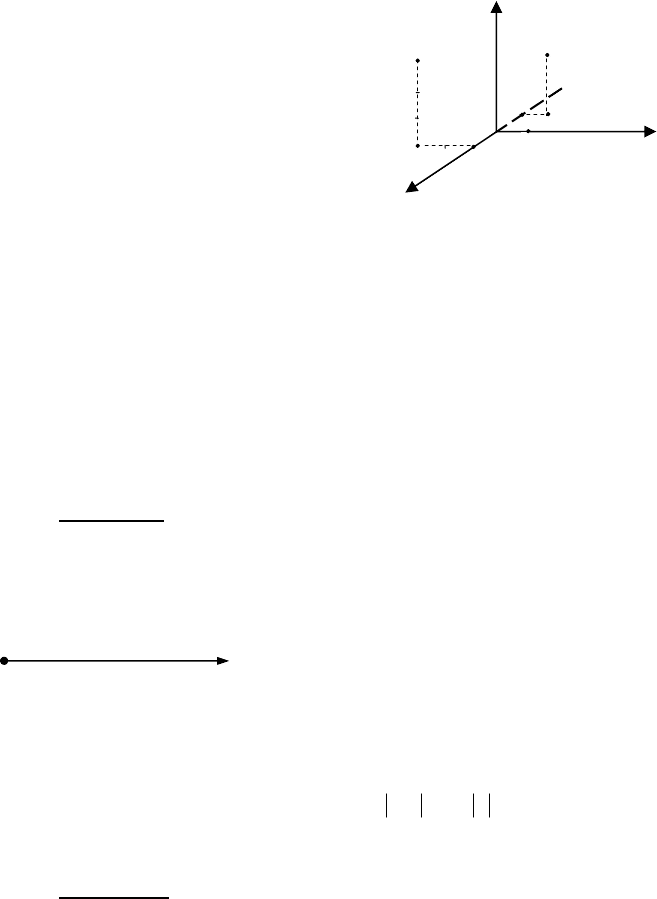
Нехай точка
M
є довільною
точкою простору (мал.9).
Знайдемо проекції точки
M
на координатні осі. Для цього через
точку
M
проведемо три площини,
які будуть перпендикулярні до ко-
ординатних осей
Oy,Ox
та
Oz
.Нехай ці площини перетинають вісі Oy,Ox і
Oz
відповідно в
точках
B,A
і
.C
Тоді координата
x
точки
A
на осі
Ox
називається
абсцисою точки
M
, координата
y
точки
B
на числовій вісі
Oy
називається ординатою точки
M
, а координата z точки C на
числовій вісі
Oz називається аплікатою точки
M
. Значить, величи-
ни направлених відрізків
ОА
,
ОВ
та
ОС
, тобто числа x,y,z є коор-
динатами точки
M.
Таким чином, в даній системі координат кожній точці
M
простору відповідає єдина упорядкована трійка чисел
( )z;y;x . В
цьому записі
x
означає перше число,
y
- друге,
z
- третє. І навпаки,
кожній упорядкованій трійці чисел (
)z;y;x відповідає тільки одна
точка простору
M. Отже, прямокутна система координат в просторі
встановлює взаємно однозначну відповідність між множиною всіх
точок простору і множиною упорядкованих трійок чисел.
Площини
Oxy, Oyz, і Oxz називаються координатними
площинами і поділяють весь простір на вісім частин.
Приклад 1. Побудувати точки
M
1
(1;–2;3), M
2
(–1;1;2).
A
C
M
z
0
x
y
Мал.9
B
95
Розв
’язування. На вісі Ox відкладаємо відрізок 1OA = . Через
точку
A
проводимо пряму,
паралельну вісі
Oy і на ній
відкладаємо відрізок
AB= -2. Через
точку
B проводимо пряму, паралельну
вісі
Oz і відкладаємо відрізок BM
1
=3
Кінець цього відрізка дає шука-
ну точку
M
1
(мал.10). Точка M
2
(-1;1;2)
будується аналогічно.
§ 4. Скалярні і векторні величини
У фізиці, математиці, економіці і інших науках зустрічаються
величини двох видів: одні з них характеризуються тільки числом, а
інші – числом і напрямом в просторі.
Величини називаються скалярними або скалярами, якщо кож-
на із них визначається своїм числовим значенням у вибраній системі
одиниць, наприклад, довжина,
площа, об’єм, час, температура.
Величини називаються векторними або векторами, якщо кож-
на із них визначається числовим значенням і напрямом. Наприклад,
сила, швидкість, прискорення.
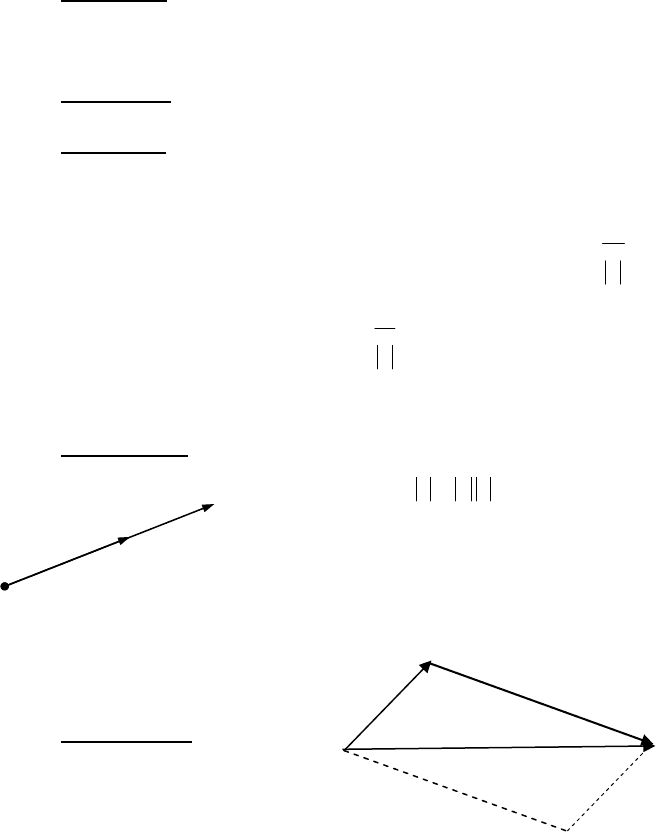
Означення. Напрямлений відрізок прямої називається век-
тором.
Вектор будемо позначати символом
→
AB
. Перша буква означає по-
чаток вектора, а друга – його кінець. Вектор також будемо познача-
ти однією малою буквою з стрілкою на
верху, наприклад
→
a (мал.11).
Якщо початок і кінець вектора
співпадають, то вектор називається нульовим і позначається
→
0
або
просто
0.Віддаль між початком і кінцем вектора називається його
довжиною , або модулем і позначається
→
AB
або
→
а
.
Ми будемо вивчати вільні вектори. Такий вектор можна пере-
носити по його лінії дії або паралельно самому собі.
Означення. Вектори, які знаходяться на паралельних пря-
мих, або на одній і тій же прямій, називаються колінеарними.
Мал.11
В
А
→
a
M
2
A
М
1
z
0
x
y
Мал.10
B
1
1
96
Означення. Вектори, які знаходяться на паралельних площи-
нах або на одній і тій же площині, називаються компланарними.
Відповідно, компланарні вектори, які приведені до одного і
того ж початку, будуть знаходитися на одній площині.
Означення. Два вектори рівні, якщо вони однаково
напрямлені і модулі їх рівні .
Означення. Два вектори, в яких модулі рівні, а напрямки
протилежні, називаються протилежними
→
a і (
→
− a ).
Одиничний вектор (орт) вектора
→
a
дорівнює
→
→
а
a
і
позначається так:
.
а
a
a
→
→
→
=
§5.Дії над векторами
а
) Добуток вектора на число.
Означення 1. Добутком вектора
→
a
на число λ називається
вектор
→→
λ= ab
, який має довжину
→→
λ= ab
і напрям його
співпадає з напрямом вектора
→
a
, якщо
0>λ
і протилежний йому, якщо
0<λ
(
мал.12).
Умова
→→
λ= ab (2.6)
є умовою колінеарності двох
векторів.
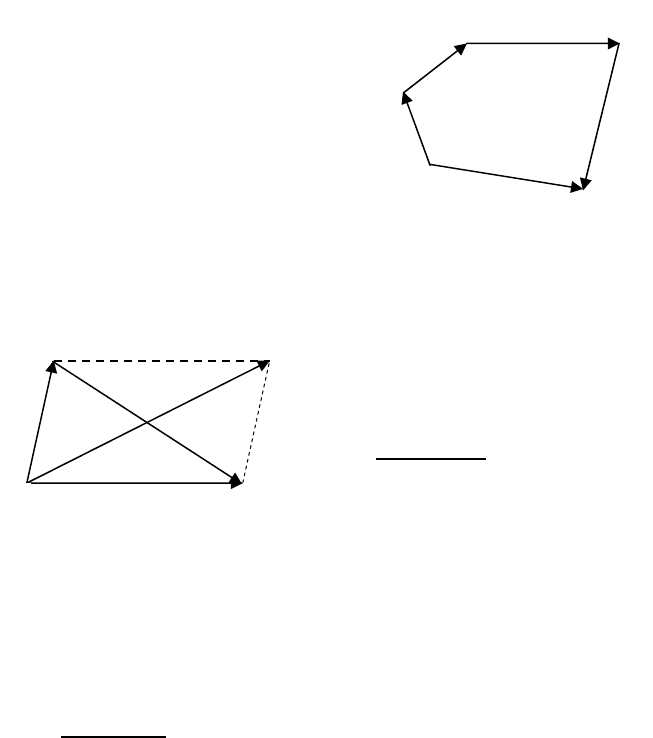
б) Додавання векторів.
Означення 2. Сумою двох
векторів
→
a і
→
b називається век-
тор
→→→
+= baс , початок якого
співпадає з початком вектора
→
a
, а кінець співпадає з кінцем вектора
→
b
, при умові що початок
вектора
→
b
співпадає з кінцем вектора
→
a
(правило трикутника)
(
мал.13).
)0(ab >λλ=
→→
→
a
Мал.12
Мал.13
→
a
→
b
→→→
+
=
b
a
c
→
b
97
Зрозуміло, що вектор
→
с в цьому випадку є діагоналлю пара-
лелограма, побудованого на векторах
→
a і
→
b (правило паралелогра-
ма) (мал.13).
Для векторної суми справедливий переставний закон
→→→→
+=+ .abba
Легко переконатися, що для
векторної суми має місце сполучний
закон.
)cb(ac)ba(
→→→→→→
++=++
.
Виходячи з означення 2, легко
знаходимо суму, наприклад, чотирьох
векторів .d,c,b,a
→→→→
(мал.14).
Вектор
→
e сполучає початок першого вектора
→
a з кінцем век-
тора
→
d (правило многокутника).
в
) Віднімання векторів.
Дію віднімання векторів
можна розглядати як обернену дію
щодо додавання векторів.
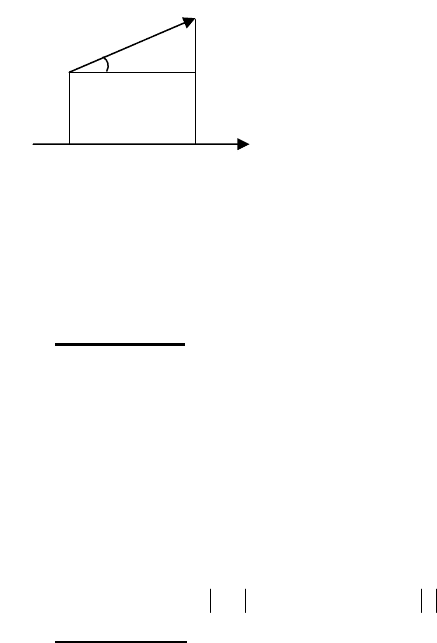
Означення. Різницею
→→
− ba
називається вектор
→
с , який в
сумі з вектором
→
b дає вектор
→
a (мал.15), тобто
→→→
=− .сba
Як видно з мал.15, що одна діагональ
→
OC є сумою
→→
+ ba , а
друга діагональ
→
BA
є різницею векторів
→
a і
→
b .
Дамо ще одне означення різниці векторів.
Означення. Різницею двох векторів
→
a
і
→
b
, які мають
спільний початок, називається вектор
→
с
, який сполучає кінці
цих векторів і напрямлений в сторону зменшуваного.
→
c
→
a
→
e
→
b
→
d
Мал.14
→→→
−=
b
a
c
Мал.15
→
a
→
b
→
→
+
b
a
О
А
В
С
98
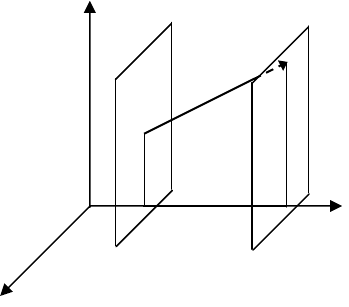
§6. Проекція вектора на вісь
Нехай маємо довільну вісь
l на площині і деякий вектор
→→
= aAB
(мал.16).
Опустимо із початку
A
век-
тора і з кінця
B
перпендикуляри на
вісь
l . Основами перпендикулярів
будуть точки
1
A
і
1
B
, які назива-
ються проекціями точок
A
і
B
.
Величина
11
BA
називається
проекцією вектора
→
AB
на вісь
l
і позначається
→
ABПр
l
, тобто
=
11
BA
→
ABПр
l
.
Означення 1. Проекцією вектора
→
a на вісь l називається
величина відрізка
11
BA взята із знаком плюс, якщо напрям відріз-
ка
11
BA
співпадає з напрямом вісі l , і з знаком мінус, якщо на-
прями протилежні.
З точки
A
проведемо пряму, паралельну осі l , яка перетне ві-
дрізок
1
BB
в точці C .Вектор
→
a
утворює з віссю l кут
ϕ
. Величина
відрізка
AC дорівнює величині відрізка
11
BA , а тоді з ABCΔ зна-
ходимо
ϕ=
→→
cosABABПр
l
або ϕ=
→→
cosaaПр
l
(2.7)
Означення 2. Проекція вектора на будь-яку вісь дорівнює
добутку довжини цього вектора на косинус кута між віссю і ве-
ктором.
Якщо кут
ϕ
гострий, то проекція
→
aПр
l
додатне число, а якщо
кут
ϕ
тупий, то проекція
→
aПр
l
- від’ємне число.
◙ Властивості проекцій.
1. Якщо вектори
→
a і
→
b рівні, то величини їх проекцій на одну
й ту ж вісь
l також рівні, тобто .bПрaПр
ll
→→
=
В
1
А
1
Мал.16.
φ
→
a
А
В
С
l
99
2. Проекція суми векторів на будь-яку вісь дорівнює сумі
проекцій доданків на ту ж вісь, тобто
.cПрbПрaПр)cba(Пр
llll
→→→→→→
++=++
3. Проекція різниці двох векторів на вісь
l дорівнює різниці
величин проекцій на ту ж вісь, тобто
.bПрaПр)ba(Пр
lll
→→→→
−=−
4.
Якщо вектор
→
a
помножений на будь-яке число
λ
, то вели-
чина проекції вектора
→
a
на вісь
l
також помножиться на число
λ
,
тобто
.aПр)a(Пр
ll
→→
λ=λ
§ 70. Проекції вектора на осі координат
Розглядається прямокутна сис-
тема координат
Oxyz в прос-
торі і довільний вектор
.AB
→
Нехай
,xABПр
x
=
→
,yABПр
y
=
→
.zABПр
z
=
→
Проекції
z
,
y
,
x
вектора
→
AB
на
координатні осі називають
ко-
ординатами вектора і запису-
ють
)z,y,x(AB =
→
.
Якщо задані дві точки
)z;y;x(A
111
і
)z;y;x(B
222
, то коор-
динати вектора
→
AB
знаходяться за формулами
,xxx
12
−= ,yyy
12
−= .zzz
12
−=
Дійсно, проведемо через точки
A
і
B
площини,
перпендикулярні до осі
Ox
і позначимо точки їх перетину
відповідно
1
A
і
1
B
(мал.17). Точки
1
A
і
1
B
мають на осі Ox коорди-
нати
1
x і
2
x , але
1211
xxBA −= на основі формули (2.1) , а тому
.xxx
12
−=
Аналогічно доводиться, що
,yyy
12
−= .zzz
12
−=
А
1
А
О
В
x
1
у
z
х
В
1
x
2
Мал.17.
100
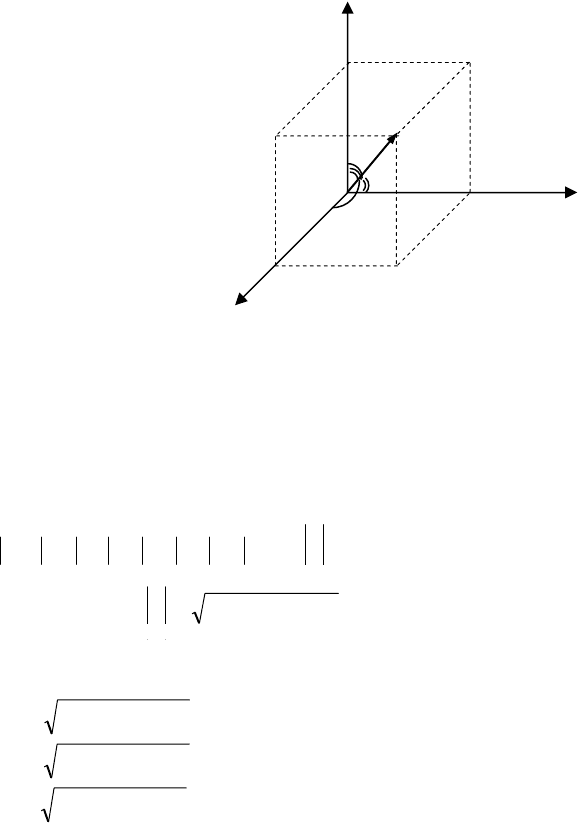
§8. Напрямні косинуси вектора
Нехай маємо вектор
→→
= OM)z;y;x(a
111
і будемо вважати, що
він виходить з початку ко-
ординат і не знаходиться ні
в одній координатній
площині. Через точку
M
проведемо площини,
перпендикулярні до осей
координат і разом з коорди-
натними площинами вони
утворять паралелепіпед,
діагональ якого відрізок
OM
(мал.18). Через
γ
β
α ,,
позначимо кути, які утворює
вектор
→→
= OMa з осями ко-
ординат. Величини
γ
β
α cos,cos,cos називаються напрямними ко-
синусами вектора
.a
→
Координати вектора
,OAx
1
= ,OВу
1
= .OCz
1
=
Квадрат діагоналі прямокутного паралелепіпеда дорівнює
сумі квадратів довжин трьох його вимірів.
Тому
2222
OCOBOAOM ++= або
2
1
2
1
2
1
2
zyxа ++=
→
2
1
2
1
2
1
zyxа ++=
→
(2.8)
Формула (2.8) виражає довжину вектора через його координа-
ти. Тоді на основі формул (2.7) і (2.8) будемо мати
;coszyxx
2
1
2
1
2
11
α++=
;coszyxy
2
1
2
1
2
11
β++=
.coszyxz
2
1
2
1
2
11
γ++=
Звідси для напрямних косинусів одержуємо
→
а
M
C
В
А
γ
О
у
z
х
Мал.18.
α
β
