Шинкарик М.І. Вища математика

Подождите немного. Документ загружается.

371

,yy

101

,yy

101

′

,yy

202

= .yy

202

′

Тоді

⎩

⎨

⎧

′

0202101

yyСyС

Розв’яжемо цю систему відносно

С і

С , одержимо:

200200

20102010

200200

yyyy

′

−

′

−

′

−

′

yyyy

010010

20102010

010010

′

−

′

−

′

−

′

Оскільки

≠Δ , бо система розв’язків

y і

y фундаменталь-

на, то для

С і

С справді знайдемо потрібні значення.

Таким чином, з розв’язку

2211

yСyСy += можна знайти будь-

який частинний розв’язок, тобто розв’язок, що відповідає будь-яким

початковим умовам, а це означає, що розв’язок

2211

yСyСy += є

загальним розв’язком рівняння (7.24).

3.2 Лінійні неоднорідні диференціальні рівняння

другого порядку

Означення. Лінійним неоднорідним диференціальним рів-

нянням другого порядку називається рівняння :

)x(fy)x(g'y)x(p''y =++ , (7.27)

де функція f(x) називається правою частиною рівняння.

Рівняння

0y)x(g'y)x(p''y =++ , яке одержується із рівнян-

ня(7.27), коли

f(x)=0, називається однорідним рівнянням, що відпо-

відає рівнянню (7.27).

ТЕОРЕМА

( про структуру розв’язку неоднорідного дифе-

ренціального рівняння). Загальний розв’язок неоднорідного ди-

ференціального рівняння другого порядку дорівнює сумі зага-

льного розв’язку відповідного лінійного однорідного диференці-

ального рівняння і будь-якого частинного розв’язку лінійного

неоднорідного диференціального рівняння другого порядку.

Надалі будемо користуватись позначенням:

y=y

з.о

ч.н

(7.28)

де

- загальний розв’язок лінійного неоднорідного диференціаль-

ного рівняння другого порядку;

.о.з

y - загальний розв’язок відповід-

372

ного однорідного диференціального рівняння;

.н.ч

- будь-який час-

тинний розв’язок лінійного неоднорідного рівняння.

Доведення

. Знайдемо похідні:

.н.ч.о.з

yyy

′

.н.ч.о.з

yyy

′′

Підставимо

.н.ч.о.з

yyy +=

і знайдені похідні

y,y

′′′

в рівнян-

ня(7.27), матимемо

)x(f)yy)(x(g)yy)(x(pyy

.н.ч.о.з.н.ч.о.з.н.ч.о.з

=++

′

′′

або

)x(fy)x(gy)x(рyy)x(gy)x(py

.н.ч.н.ч.н.ч.о.з.о.з.о.з

′

′′

′

′′

Оскільки

.о.з

y є загальним розв’язком однорідного рівняння

0y)x(g'y)x(p''y =++

, то в останній рівності

0y)x(g'y)x(p''y

.о.з.о.з.о.з

=++ .

А з того, що

.н.ч

- частинний розв’язок рівняння (7.27), мати-

мемо тотожність:

)x(fy)x(g'y)x(p''y

.н.ч.н.ч.н.ч

=++ .

Отже, ми довели, що функція

.н.ч.о.з

yyy += - розв’язок дифе-

ренціального рівняння (7.27)

Легко показати, що кожний розв’язок рівняння (7.27), який

задовольняє будь-які початкові умови (з певної області їх визначен-

ня), можна знайти з функції

.н.ч.о.з

yyy += . Отже, ця функція є за-

гальним розв’язком. Довести це твердження можна аналогічно до

доведення такого ж твердження для відповідного однорідного рів-

няння, яке ми привели вище, тому тут на цьому доведенні не зупи-

няємось.

3.3. Метод варіації довільних сталих

Розглянемо метод варіації довільних сталих (метод Лагранжа)

для знаходження частинного розв’язку неоднорідного диференці-

ального рівняння.

Суть цього методу полягає в наступному: щоб знайти частин-

ний розв’язок неоднорідного лінійного рівняння (7.27), досить у ви-

раз для загального розв’язку

y=C

(x)+C

(x) відповідного одно-

рідного рівняння замість сталих

і C

підставити функції незалеж-

ної змінної

x, похідні від яких

)x(С

′

)x(С

′

задовольняють таку

систему алгебраїчних рівнянь:

⎩

⎨

⎧

′′

′

).x(f)x(y)x(C)x(y)x(

,0)x(y)x(С)x(y)x(С

2211

373

Доведемо це твердження.

Запишемо розв’язок диференціального рівняння у вигляді:

y=C

(x)+C

(x)

Знайдемо похідну:

)x(y)x(C)x(y)x(C)x(yC)x(yCy

22112211

′

Ми хочемо визначити дві функції

(x) і C

(x).

Одне співвідношення між ними ми можемо вибрати довіль-

ним. Поставимо вимогу, щоб

(x) і C

(x) задовольняли рівність

0)x(y)x(C)x(y)x(C

2211

′

тоді

)x(y)x(C)x(y)x(Cy

2211

′

Знайдемо другу похідну:

).x(y)x(C)x(y)x(C)x(y)x(C)x(y)x(Cy

22112211

′′

Підставимо значення

y,y′,y″в диференціальне рівняння (7.27),

будемо мати

).x(f)x(y)x(C)x(y)x(C())x(yp

)x(y

р)x(y)(x(C))x(yр)x(yр)x(y)x(C

221122

2122121111

′′

′

′′

′

⋅+

′′′

Оскільки

(x) та y

(x) є розв’язками однорідного рівняння, то

вирази :

0)x(yp)x(yp)x(y

12111

′

′′

0)x(yp)x(yp)x(y

22212

′

′′

Звідси

)x(f)x(y)x(C)x(y)x(C

2211

′′

Отже, для того щоб функція

)x(y)x(C)x(y)x(Cy

2211

яка задовольняє умову

0)x(y)x(C)x(y)x(C

2211

′

, була

розв’язком рівняння (7.27), необхідно і достатньо, щоб

виконувалась рівність:

)x(f)x(y)x(C)x(y)x(C

2211

′′

Таким чином дістаємо систему

⎩

⎨

⎧

′′

′

),x(f)x(y)x(C)x(y)x(C

,0)x(y)x(C)x(y)xC

2211

221(1

з якої визначаємо

)x(C

′

та )x(C

′

. Ця система має єдиний

розв’язок, бо за нашим припущенням

(x) та y

(x) -лінійно незалеж-

ні розв’язки однорідного рівняння.

Нехай

)x()x(C

′

)x()x(C

′

, тоді, інтегруючи,

одержимо

∫

+ϕ=

Сdx)x()x(C ,

∫

+ϕ=

Сdx)x()x(C , де

,С

С - довільні сталі. Підставимо знайдені )x(С

і )x(С

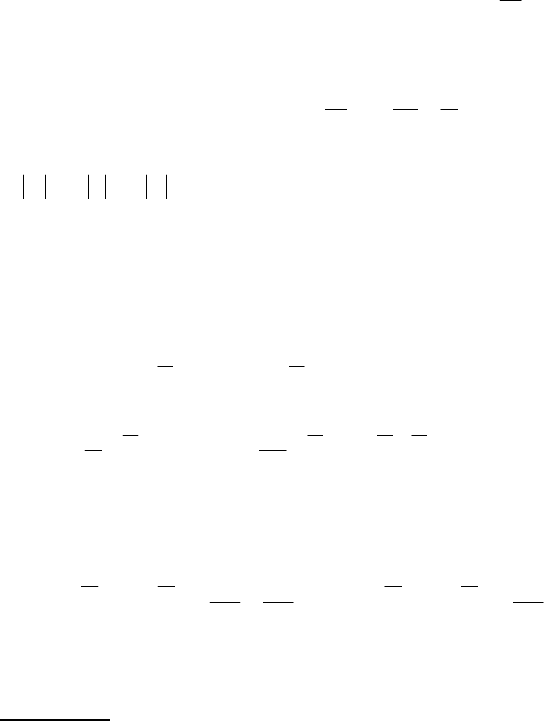
374

співвідношення

)x(y)x(С)x(y)x(Сy

2211

і отримаємо загаль-

ний розв’язок диференціального рівняння (7.27).

Приклад

. Знайти загальний розв’язок рівняння x

y =

′

−

′′

Розв

’язування. Знайдемо загальний розв’язок цього рівняння

методом варіації довільних сталих. Знайдемо загальний розв’язок

відповідного однорідного рівняння 0

y =

′

−

′′

′

′′

Інтегруючи обидві частини рівняння, одержимо

;Clnxlnyln +=

′

Cxy =

′

, звідки

CxCy += .

Тепер припустимо, що

C і

C є функціями від

і складаємо

систему для знаходження

)x(C

′

і )x(C

′

⎩

⎨

⎧

′

.xx)x(C2

,0)x(Cx)x(C

Звідки

)x(C

′

)x(C

−=

′

В результаті інтегрування, маємо

)x(C

)x(C +−= , де

C,C - довільні сталі.

Підставляємо )x(C

і )x(C

в загальний розв’язок відповід-

ного однорідного рівняння

)x(Cx)x(Cy

221

+= ,

одержимо загальний розв’язок даного рівняння:

СxСy

−++= або

СxСy

++= .

3.4. Лінійні однорідні диференціальні рівняння другого

порядку з сталими коефіцієнтами

Означення. Рівняння вигляду

0gy'py''y =++ , (7.29)

де p,g- сталі числа, називається лінійним однорідним диференці-

альним рівнянням другого порядку з сталими коефіцієнтами.

Знайдемо загальний розв’язок цього рівняння. За теоремою

про структуру загального розв’язку лінійного однорідного диферен-

ціального рівняння другого порядку маємо:

y=C

(x)+C

(x),

де y

(x),y

(x) - лінійно незалежні частинні розв’язки.

375

Частинний розв’язок рівняння (7.29) будемо шукати у вигляді

ey = , k - стала , яку треба знайти.

Знайдемо

key =

′

kx2

eky =

′′

і підставимо в рівняння (7.29),

маємо:

.0)gpkk(e

2kx

=++ Оскільки 0e

≠ завжди, то

0gpkk

=++ . (7.30)

Рівняння (7.30) називається характеристичним рівнянням для

диференціального рівняння (7.29).

Позначимо через

k,k

- корені характеристичного рівняння.

При розв’язанні характеристичного рівняння, яке є квадратним рів-

нянням відносно

k , можливі три випадки:

1) Корені характеристичного рівняння дійсні, різні:

kk ≠

)0D( > .

2) Корені характеристичного рівняння дійсні, рівні:

kk =

)0D( =

3) Корені характеристичного рівняння комплексні числа

2,1

±α=

, )0D( < .

Розглянемо кожен випадок окремо.

1)Корені характеристичного рівняння дійсні, різні:

kk ≠ .

Частинними розв’язками рівняння (7.29) в цьому випадку бу-

дуть функції

ey = та

ey = .

Ці розв’язки лінійно незалежні, бо

.conste

x)kk(

≠==

−

Отже, загальний розв’язок рівняння (7.29) запишеться

eCeCy += . (7.31)

Приклад

1. Розв’язати диференціальне рівняння

0y2yy =−

′

′′

Розв

’язування. Складаємо характеристичне рівняння:

.02kk

=−+

Тут корені 2k;1k

−== -дійсні, різні. Загальний

розв’язок диференціального рівняння запишеться:

eCeCy

−

2) Корені характеристичного рівняння дійсні, рівні:

kk = .

Один частинний розв’язок може бути

ey = .

376

Розв’язок

e лінійно залежний з першим

e , тому його

розглядати в якості другого частинного розв’язку не можна. Будемо

шукати другий частинний розв’язок у вигляді

e)x(uy = , де

)x(u - невідома функція, яку можна знайти.

Знайдемо

′

та

′′

),uku(euekeuy

xkxk

111

′

)ukuk2u(euekeuk2euy

xkxk

1111

′

′′

′

′′

і підста-

вимо в рівняння (7.29):

.0)u)qpkk(u)рk2(u(e

=+++

′

′′

Оскільки

k - кратний корінь характеристичного рівняння

(7.30), то

.0qpkk

=++

Крім того

−== або

pk2

−=

.0pk2

Отже, для того, щоб знайти

)x(u , треба розв’язати рівняння

0ue

′′

або

.0u =

′′

Інтегруючи двічі, одержимо

.BАxu += Якщо покласти ,0B,1A == то

Таким чином, в якості другого частинного розв’язку будемо

брати функцію

xey = .Розв’язки

y та

y будуть лінійно неза-

лежними, бо

.constx

≠=

Отже, загальний розв’язок диференціального рівняння (7.29)

буде :

)xCC(exeCeCy

xkxk

111

+=+= . (7.32)

Приклад

2. Розв’язати диференціальне рівняння

.0y4y4y =+

′

−

′′

Розв

’язування. Характеристичне рівняння ,04k4k

=+− ко-

рені якого

2kk

== - дійсні, рівні.

Загальний розв’язок диференціального рівняння буде:

)xCC(exeCeCy

x2x2

+=+= .

3) Корені характеристичного рівняння комплексні числа.

Якщо дискримінант характеристичного рівняння

0D < , то

дійсних коренів це рівняння не має.Введемо поняття комплексного

377

числа. Будь-яке комплексне число можна представити у вигляді:

+α= де 1i −= або .1i

−=

При цьому α

- називається дійсною частиною комплексного

числа; β - уявною частиною комплексного числа .

Числа

+α=

та

−α=

називаються комплексно

спряженими числами.

Повернемось тепер до розв’язання характеристичного

рівняння (7.30), дискримінант якого менший нуля. Тоді його корені

будуть комплексно спряженими числами, тобто

2,1

±α= .

У випадку, коли

+α= , розв’язок диференціального

рівняння буде

xixx)i(

eeey

βαβ+α

⋅== .

Якщо алгебраїчне рівняння з дійсними коефіцієнтами має корінь

+α= , то воно має і спряжений з ним корінь ik

−α= ,

а тому

xixx)i(

eeey

β−αβ−α

⋅== .

За формулами Ейлера :

xsinixcose

±=

,запишемо функції

y та

y у вигляді:

,xsiniexcose)xsinix(cosey

xxx

β+β=β+β=

ααα

xsiniexcose)xsinix(cosey

xxx

β−β=β−β=

ααα

Далі використаємо таку теорему.

Теорема

. Якщо диференціальне рівняння (7.29) має

розв’язком функцію )x(iv)x(u + , то кожна з функцій )x(u і

)x(v

є розв’язком рівняння (7.29).

Доведення. Дійсно, підставимо функцію )x(iv)x(u + в

рівняння (7.29), маємо

0))x(iv)x(u(q))x(iv)x(u(p))x(iv)x(u( ≡++

′

′′

або 0)qvvpv(i)quupu( ≡+

′

′′

′

′′

Але комплексна функція дорівнює тотожно нулю тоді і тільки

тоді, коли рівні нулю її дійсна і уявна частини, тобто:

,0quupu =+

′

′′

.0qvvpv =+

′

′′

А це означає, що

)x(u і )x(v є розв’язками рівняння (7.29).

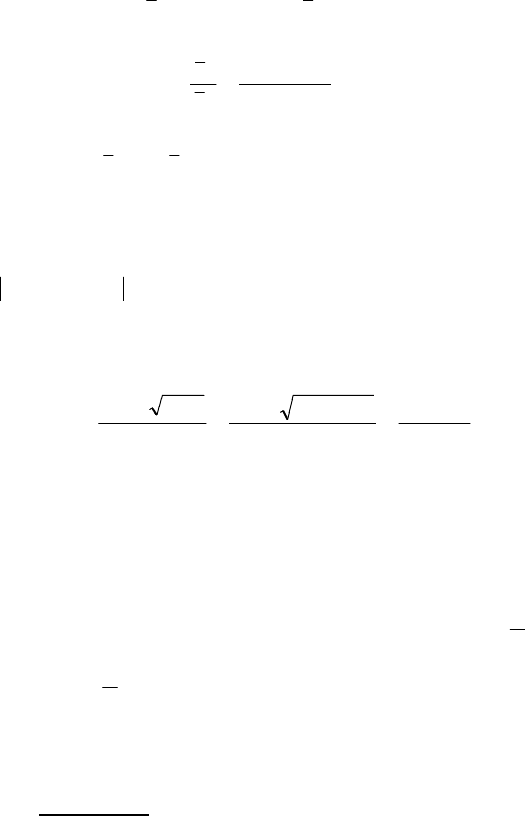
378

На основі доведеної вище теореми, частинними розв’язками

будуть функції

xcosey

β=

, xsiney

β=

, причому вони бу-

дуть лінійно незалежними, бо

.constxctg

xsine

xcose

≠β=

Отже, загальний розв’язок рівняння(7.29) буде

xsineСxcoseСyСyСy

12211

β+β=+=

αα

або

)xsinСxcosС(ey

β+β=

. (7.33)

Приклад

3. Знайти частинний розв’язок диференціального рів-

няння

,0y5y2y =+

′

′′

що задовольняє таким початковим умовам

,0y

′

Розв

’язування. Шукаємо спочатку загальний розв’язок. Для

цього складаємо характеристичне рівняння і розв’язуємо його:

,05k2k

=++

,016204D <−=−=

i21

i42

)1(162

162

2,1

±−=

±−

−⋅±−

−±−

= -

корені комплексно спряжені числа. Загальний розв’язок запишеться:

)x2sinCx2сosC(ey

−

Знайдемо частинний розв’язок, використовуючи початкові

умови :

)),02sin(C)02cos(C(e0

⋅+⋅=

−

= ;

;x2sinCex2сosC2ey

x −−

−⋅=

′

,C21

= ,

звідки

.x2sine

x−

3.5 Лінійні неоднорідні диференціальні рівняння другого

порядку з сталими коефіцієнтами

Означення. Рівняння

)x(fgy'py''y =++

, (7.34)

де

- сталі числа, 0)x(f ≠ , називається лінійним

неоднорідним диференціальним рівнянням другого порядку з ста-

лими коефіцієнтами.

За теоремою про структуру розв’язку лінійного неоднорідного

379

рівняння другого порядку загальний розв’язок рівняння (7.34) є су-

мою загального розв’язку відповідного однорідного рівняння і будь-

якого частинного розв’язку неоднорідного рівняння. Це твердження

записано формулою (7.28):

.н.ч.о.з

yyy +=

Загальний розв’язок однорідного рівняння ми детально розг-

лянули вище. Тепер перейдемо до знаходження частинного

розв’язку неоднорідних рівнянь із спеціальною правою частиною,

розв’язок яких можна знайти не вдаючись до інтегрування.

1) Нехай права частина рівняння (7.34) має вигляд

e)x(P)x(f

= , де )x(P

- многочлен n-го степеня. Тут можливі

два випадки:

а)

- не є коренем характеристичного рівняння, тоді

н.ч

e)x(Qy

, де

)x(Q

- многочлен n-го степеня із неозначе-

ними коефіцієнтами.

б)

α - є коренем характеристичного рівняння кратності

(

= або

= ) , тоді

н.ч

e)x(Qxy

= .

Зауваження

. Якщо

)x(P)x(f

, то вважаємо , що 0=α і

перевіряємо , чи 0 є коренем характеристичного рівняння.

Приклад

1. Знайти загальний розв’язок рівняння

xe4yyy2 =−

′

−

′′

. (7.35)

Розв

’язування. Загальний розв’язок шукаємо у вигляді

.н.ч.о.з

yyy +=

Спочатку знайдемо загальний розв’язок

.о.з

відповідного

однорідного рівняння:

;0yyy2 =−

′

−

′′

;01kk2

=−−

k,1k

−== ,

о.з

eCeCy

−

+= .

Частинний розв’язок

.н.ч

неоднорідного рівняння шукаємо у

вигляді правої частини рівняння, а саме

н.ч

e)BAx(y +=

оскільки

2=α

не є коренем характеристичного рівняння. Тут

потрібно знайти неозначені коефіцієнти

та В . Для цього знайде-

мо

)y(

.н.ч

′

та )y(

.н.ч

′′

, маємо:

;Ae)BAx(e2)y(

x2x2

н.ч

⋅++=

′

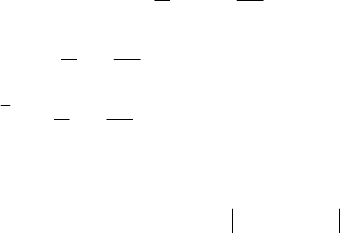
380

x2x2x2x2x2

н.ч

Ae4)BAx(e4Ae2Ae2)BAx(e4)y( ++=⋅+⋅++=

′′

Підставляємо

.н.ч

y , )y(

.н.ч

′

та )y(

.н.ч

′′

у рівняння (7.35), одержимо

.xe4BeAxeAeBe2Axe2Ae8Be8Axe8

x2x2x2x2x2x2x2x2x2

=−−−−−++

Розділимо ліву і праву частини рівняння на

e , маємо :

,x4BAxAB2Ax2A8B8Ax8 =−−−−−++

x4A7B5Ax5 =++ .

Відомо, що многочлени рівні між собою тоді і тільки тоді, ко-

ли рівні їх коефіцієнти при однакових степенях

лівої і правої час-

тини, тобто

⎩

⎨

⎧

0B5A7

4A5

, звідки

A −==

Отже,

.н.ч

⎟

⎠

⎞

⎜

⎝

⎛

−=

і загальний розв’язок буде

eCeCy

⎟

⎠

⎞

⎜

⎝

⎛

−++=

−

Приклад

2. Знайти розв’язок диференціального рівняння

x1yy2y +=+

′

−

′′

, (7.36)

який задовольняє початковим умовам

;2y

−=

′

Розв

’язування. Тут характеристичне рівняння 01k2k

=+−

має дійсні, рівні корені

1kk

, тому загальний розв’язок

відповідного однорідного рівняння буде

.e)xCC(y

21.

о.з

Права частина рівняння (7.36) має вигляд

,x1)x(P

+= при-

чому

0=α не є коренем характеристичного рівняння, тому частин-

ний розв’язок рівняння будемо шукати у вигляді

.BAxy

.н.ч

Продиференціювавши

.н.ч

, підставимо у рівняння

(7.36), маємо :

,x1BАxA2 +=++−

звідки

;1A =

;1BA2 =+−

.3B =

Частинним розв’язком заданого рівняння є функція

,3xy

.н.ч

а його загальним розв’язком функція

)3x(e)xCC(y

+++=

Знайдемо тепер частинний розв’язок рівняння (7.36), який

задовольняє заданим початковим умовам. Для цього знайдемо

1eСe)xCC(y

+++=

′

, тоді