Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

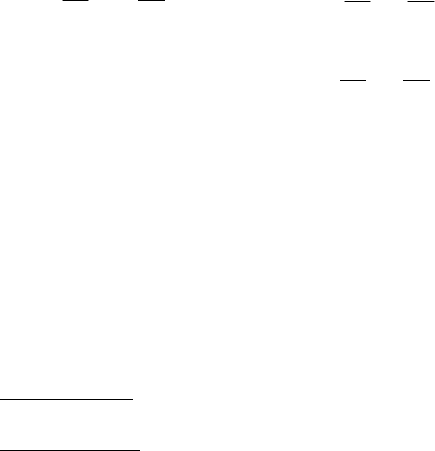
381
⎩
⎨
⎧
++=−
+=
.1CC3
,3C2
21
1
Звідки 1С
1
−= , 3С
2
−= .
Шуканим частинним розв’язком буде
.3xe)x31(y
x
.
н.ч
+++−=
Приклад
3. Розв’язати диференціальне рівняння:
x
e)2x(y6y7y −=+
′
−
′′
.
Розв
’язування. Знайдемо загальний розв’язок відповідного
однорідного рівняння :
06k7k
2
=+− ,
;1k
1
= ;6k
2
=
x6
2
x
1.
о.з
eCeCy +=
.
Частинний розв’язок неоднорідного рівняння шукаємо у
вигляді
x
.
н.ч
e)BAx(xy += , бо 1=α є коренем характеристичного
рівняння. Виконавши необхідні обчислення, знайдемо
.
25
9
B,
10
1
A
=−=
Тоді
x
.н.ч
e
25
9
x
10
1
xy
⎟
⎠
⎞
⎜
⎝
⎛
+−=
.
Отже, загальний розв’язок заданого рівняння буде
.e
25
9
x
10
1
xeCeCy
xx6
2
x
1
⎟
⎠
⎞
⎜
⎝
⎛
+−−+=
2) Нехай права частина рівняння (7.34) має вигляд
)xsin)x(Rxcos)x(P(e)x(f
mn
x
β+β=
α
.
Перевіряємо чи
α+βі є коренем характеристичного рівняння:
а)
α+βі не є коренем характеристичного рівняння, тоді
),xsin)x(Nxcos)x(L(ey
kk
x
.н.ч
β+β=
α
,
де
L
k
(x), N
k
(x), - многочлени k-го степеня з неозначеними
коефіцієнтами
(k=max(m,n)).
б)
α+βі є коренем характеристичного рівняння, тоді
)xsin)x(Nxcos)x(L(xey
kk
x
.н.ч
β+β=
α
.
Зауваження
1. Якщо α=0, то перевіряємо, чи β є коренем ха-
рактеристичного рівняння.
Зауваження
2. Якщо в правій частині є одна із тригономет-
ричних функцій, наприклад,
cosx, то в частинний розв’язок повинна
входити і функція
sinx.
Приклад
4. Розв’язати диференціальне рівняння:
сosxey2yy
x
=−
′
+
′′
. (7.37)
Розв
’язування. Складаємо характеристичне рівняння і
розв’язуємо його :
02kk
2
=−+
;
2k
1
−=
,
1k
2
=
.
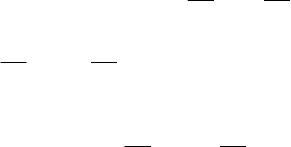
382
Загальний розв’язок однорідного рівняння
x
2
x2
1.о.з
eCeCy +=
−
.
Права частина неоднорідного рівняння
f(x)=e
x
cosx, тобто має вигляд
)xsin)x(Qxcos)x(P(e)x(f
nn
x
β+β=
α
,
де
0)x(Q,1)x(P,1,1
mn
===
β
=α
.
Оскільки α
+βі=1+і не є коренем характеристичного рівняння,
а
0)x(Q,1)x(P
mn
==
многочлени нульового степеня, то
)xsinBxcosA(ey
x
.
н.ч
+= .
Знайдемо
.н.ч
y
′
та
.н.ч
y
′′
:
)xcosBxsinA(e)xsinBxcosA(e)y(
xx
.
н.ч
+−++=
′
).xcosB2xsinA2(e
)xsinBxcosA(e)xcosBxsinA(e
)xcosBxsinA(e)xsinBxcosA(e)y(
x
xx
xx
.
н.ч
+−=
=−−++−+
++−++=
′′
Підставляємо
)y(,y
.н.ч.н.ч
′
та
)y(
.н.ч
′′
у рівняння (7.37):
.xcose)xsinBxcosA(e2)xcosBxsinA(e
)xsinBxcosA(e)xcosB2xsinA2(e
xxx
xx
=+−+−+
++++−
Скорочуючи обидві частини рівності на
x
e і зводячи подібні члени,
одержимо :
xcoscos)AB3(xsin)BA3( =−+−−
Зрівнюючи коефіцієнти при
с
osx
та xsin в обох частинах
рівняння, одержимо:
⎩
⎨
⎧
=+−
=−−
.1B3A
,0BA3
Звідки
10
3
B,
10
1
A =−=
.
)xsin
10
3
сosx
10
1
(ey
x
.
н.ч
+−= .
Загальний розв’язок рівняння (7.37) буде:
)xsin
10
3
xcos
10
1
(eeСeСy
xx
2
x2
1
+−++=
−
.
Приклад
5. Розв’язати рівняння .xeyy2y
x
=+−
′′
Розв
’язування. ,01k2k
2
=+− ,1kk
21
== )xСС(ey
21
x
.о.з
+= .
f(x)=xe
x
, α=1. Число 1- двократний корінь характеристичного
рівняння. Отже,
r=2.

383
),BAx(xey
2x
.
н.ч
+= або ).BxAx(ey
23x
.
н.ч
+=
).Bx2Ax3(e)BxAx(e)y(
2x23x
.
н.ч
+++=
′
).B2Ax6(e
)Bx2Ax3(e)Bx2Ax3(e)BxAx(e)y(
x
2x2x23x
.
н.ч
++
++++++=
′′
Підставляємо
)y(,)y(,y
.н.ч.н.ч.н.ч
′′′
в дане рівняння:
,xe)BxAx(e)Bx2Ax3(e2)BxAx(e2
)B2Ax6(e)Bx4Ax6(e)BxAx(e
x23x22x23x
x2x23x
=+++−+−
−+++++
або
,xB2Ax6 =+ звідси .0B2,1A6 ==
Отже,
.0B,
6
1
A ==
Тому
3x
.
н.ч
xe
6
1
y = ,
а
3x
21
x
xe
6
1
)xСС(ey ++= - загальний розв’язок даного
диференціального рівняння.
Приклад 6. Розв’язати рівняння
1xy3y
2
+=
′
−
′′
.
Розв
’язування. ,0k3k
2
=−
,0)3k(k =−
,3k,0k
21
==
x3
21.
о.з
eССy +=
.
,e)1x()x(f
x02
+=
.0=α Число 0 - корінь характеристичного
рівняння, тому
r=1.
Отже,
)СBxAx(xy
2
.
н.ч
++= або ;СxBxAxy
23
.
н.ч
++=
,СBx2Ax3)y(
2
.
н.ч
++=
′
.B2Ax6)y(
.н.ч
+=
′′
Підставляємо
)y(,)y(,y
.н.ч.н.ч.н.ч
′′′
в дане рівняння:
1xC2Bx4Ax6B2Ax6
22
+=−−−+ або
;1xC2B2x)B4A6(Ax6
22
+=−+−+−
⎪
⎩
⎪
⎨
⎧
=−
=−
=−
.1C2B2
,0B4A6
,1A6
Звідси
,
6
1
A −= ,
4
1
B −= .
4
3
2
1B2
C −=
−
=
Отже,
.x
4
3
x
4
1
x
6
1
y
23
.
н.ч
−−−=

384
x
4
3
x
4
1
x
6
1
eССy
23x3
21
−−−+=
- загальний розв’язок даного рівняння.
Приклад
7. Знайти частинний розв’язок рівняння
),3xx(ey2y
2x
−+=
′
−
′′
що задовольняє початковим умовам
;2y
0x
=
=
.2y
0x
=
′
=
Розв
’язування. Шукаємо спочатку загальний розв’язок даного
рівняння. Для цього знайдемо
у
з.о.
та
у
ч.н.
:
,0k2k
2
=−
,0)2k(k =−
.2k,0k
21
==
Тому
x2
21.
о.з
eССy +=
.
1(),CBxAx(ey
2x
.
н.ч
=α++=
- не є коренем
характеристичного рівняння).
);BAx2(e)CBxAx(e)y(
x2x
.
н.ч
++++=
′
.A2e)BAx2(e)BAx2(e)CBxAx(e)y(
xxx2x
.
н.ч
⋅+++++++=
′′
Підставляємо
,y
.н.ч
,)y(
.н.ч
′
)y(
.н.ч
′′
у дане рівняння, одержимо:
)3xx(e)BAx2(e2
)CBxAx(e2Ae2)B2Ax4(e)CBxAx(e
2xx
2xxx2x
−+=+−
−++−+++++
або
.3xxA2CBxAx
22
−+=+−−−
Звідси
⎪
⎩
⎪
⎨
⎧
−=+−
=−
=−
.3
А2С
,1В
,1А
⇒ .1C,1B,1A =−=−=
Отже,
),1xx(ey
2x
.
н.ч
+−−=
а
)1xx(eeCCy
2xx2
21
−−−++= - загальний розв’язок даного
рівняння.
Розв’яжемо задачу Коші.
).1x2(e)1xx(eeC2y
x2xx2
2
−−++−−+=
′
Використовуємо початкові умови
⎩
⎨
⎧
−+=
++=
.11C22
,1CC2
2
21
⇒
⎩
⎨
⎧
=
=+
.1C
,1CC
2
21
⇒
⎩
⎨
⎧
=
=
.1
С
,0С
2
1
Отже,
)1xx(eey
2xx2
+−−+= - шуканий частинний
розв’язок даного диференціального рівняння, який задовольняє за-
даним початковим умовам.
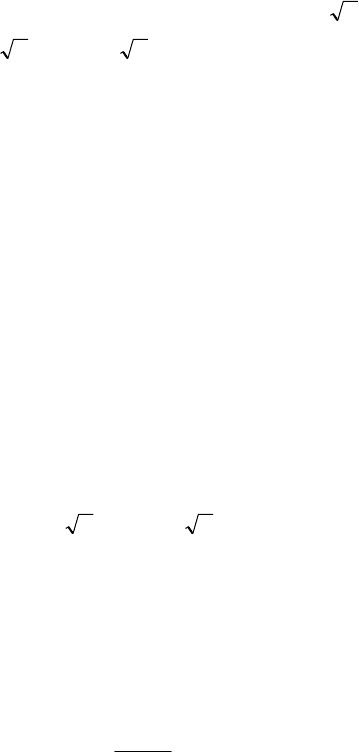
385
Приклад 8. Розв’язати рівняння
.xsin3xcosx5у2у +=+
′′
Розв
’язування.
,2k,02k
22
−==+
;і2k
2,1
±=
.x2sinСx2cosСy
21.о.з
+=
,1,0 =
β
=α ,ii =
β
+α
−i
не є коренем характеристичного рівняння.
Тому
.0r =
;xsin)DCx(xcos)BAx(y
.н.ч
+++=
;xcos)DCx(xsinCxsin)BAx(xcosA)y(
.н.ч
++++−=
′
.xsin)DCx(
xcosCxcosCxcos)BAx(xsinAxsinA)y(
.н.ч
+−
−+++−−−=
′′
Підставляємо
,y
.н.ч
,)y(
.н.ч
′
)y(
.н.ч
′′
у дане рівняння, одержимо:
.xsin3xcosx5xsinD2xsinCx2xcosB2xcosAx2
x
sin
D
x
sin
Cx
x
cos
C
2
x
cos
B
x
cos
Ax
x
sin
A
2
+=++++
+−−+−−−
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
=+
=+−
.5A
,0C
,0C2B
,3DA2
⇒
⎪
⎪
⎩
⎪
⎪
⎨
⎧
=
=
=
=
.13D
,0C
,0B
,5
А
.
Таким чином,
,xsin13xcosx5y
.н.ч
+= а загальний
розв’язок
xsin13xcosx5x2sinCx2cosCy
21
+++= .
Ми розглянули метод неозначених коефіцієнтів для
відшукання частинного розв’язку лінійних неоднорідних
диференціальних рівнянь другого порядку з сталими коефіцієнтами
із спеціальною правою частиною.
Розглянемо приклад, коли частинний розв’язок рівняння не
можна знайти методом неозначених коефіцієнтів.
Приклад
9. Розв’язати методом варіації довільних сталих
рівняння
1e
1
y2y3y
x
+
=+
′
+
′′
.
Розв
’язування. Шукаємо загальний розв’язок відповідного
однорідного рівняння. Характеристичне рівняння має вигляд
k
2
+3k+2=0, корені якого k
1
=−2; k
2
=−1, тому загальний розв’язок
однорідного рівняння запишеться:
x
2
x2
1
eСeСy
−−
+=
.
Покладемо
),x(СС
11
= )x(СС
22
= і запишемо систему
рівнянь:
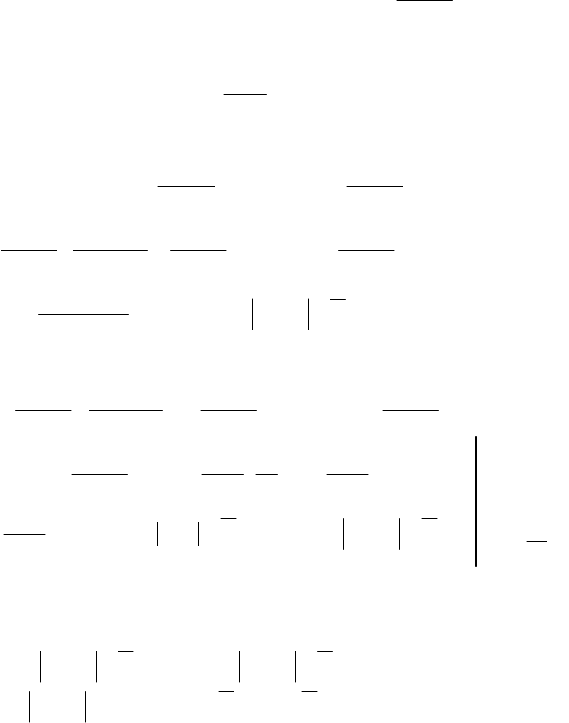
386
⎪
⎩
⎪
⎨
⎧
+
=−
′
+−
′
=
′
+
′
−−
−−
.
1
e
1
)e)(x(
Сe)2)(x(С
,0e)x(Ce)x(С
x
x
2
x2
1
x
2
x2
1
Розв’язуємо систему рівнянь відносно
)x(C
1
′
і )x(C
′
.З пер-
шого рівняння:
;
e
e
)x(С)x(С
x2
x
21
−
−
′
−=
′
;e)x(
С)x(С
x
21
⋅
′
−=
′
Підставимо
)x(С
1
′
в друге рівняння, маємо:
;
1e
1
e)x(Ce)x(С2
x
x
2
x
2
+
=
′
−
′
−−
;
1e
1
e)x(С
x
x
2
+
=
′
−
.
1e
e
)x(C
x
x
2
+
=
′
;
1e
e
dx
)x(dC
x
x
2
+
=
;dx
1e
e
)x(dC
x
x
2
+
=
;
1e
)1e(d
)x(dC
x
x
2
∫∫
+
+
=
2
x
2
C1eln)x(C ++= .
Тоді, аналогічно, знайдемо
)x(C
1
′
і відповідно )x(C
1
:
;
1e
e
)x(C
x
x2
1
+
−=
′
;
1e
e
dx
)x(dC
x
x2
1
+
−=
;dx
1e
e
)x(dC
x
x2
1
+
−=
1
xx
1
2
x
x2
1
C1elneC1tlntdt
1t
1
1
dt
1t
t
t
dt
1t
t
dx
1e
e
)x(dC
+++−=+++−=
⎟
⎠
⎞
⎜
⎝
⎛
+
−−=
=
+
−=⋅
+
−=
+
−=
∫
∫∫∫∫
Підставимо знайдені
)x(C
1
і )x(C
2
в загальний розв’язок
однорідного рівняння, одержимо загальний розв’язок даного
неоднорідного рівняння:
x
2
xx2
1
xx
e)C1e(lne)C1elne(y
−−
++++++−= або
.eCeC)ee(1elney
x
2
x2
1
xx2xx −−−−
+++++−=
§4.
Системи звичайних диференціальних рівнянь
При розв’язанні багатьох задач потрібно знайти функції
),x(yy),...,x(yy),x(yy
nn2211
===
які задовольняють систему
диференціальних рівнянь, що містять незалежну змінну
x шукані
функції
n21
y,...,y,y
і їх похідні.
t
dt
dx
dtdxe
te
x
x
=
=
=

387
Приклад. Нехай матеріальна точка маси m має криволінійну
траєкторію руху в просторі. Визначити положення точки в будь-
який момент часу
t, коли на неї діє сила .F
→
Положення точки в будь-який момент часу
t визначається її
координатами
x,y,z; отже, x,y,z є функціями від t. Проекціями векто-
ра швидкості точки на осі координат будуть похідні
.z,y,x
′′′
Покладемо, що сила
→
F
, а відповідно і її проекції
zyx
F,F,F
залежать від часу
t, від положення x,y,z точки і від швидкості руху
точки, тобто від
.
dt
dz
,
dt
dy
,
dt
dx
Шуканими невідомими функціями в
цій задачі будуть три функції
).t(zz),t(yy),t(xx === Ці
функції визначаються із рівнянь динаміки:
⎪
⎩
⎪
⎨
⎧
′′′
=
′′
′′′
=
′′
′′′
=
′′
).z,y,x,z,y,x,t(Fzm
),z,y,x,z,y,x,t(Fym
),z,y,x,z,y,x,t(Fxm
z
y
x
Ми одержали систему трьох диференціальних рівнянь другого
порядку. У випадку руху, коли траєкторія є плоска крива, що ле-
жить, наприклад, в площині
,y0x
одержимо систему двох рівнянь
для визначення невідомих функцій
)t(x та :)t(y
⎩
⎨
⎧
′′
=
′′
′′
=
′′
).y,x,y,x,t(Fym
),y,x,y,x,t(Fxm
y
x
Розглянемо найпростіші системи диференціальних рівнянь.
4.1.Системи диференціальних рівнянь першого порядку
Система
n
рівнянь першого порядку з
n
невідомими
функціями має вигляд:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
),y,...,y,y,x(f
dx
dy
........................................
),y,...,y,y,x(f
dx
dy
),y,...,y,y,x(f
dx
dy
n21n
n
n212
2
n211
1
(7.38)
388
де
x
- незалежна змінна, y
1
,y
2,
…,y
n
- невідомі функції.
Якщо в лівій частині рівнянь системи стоять похідні першого
порядку, а праві частини рівнянь зовсім не містять похідних, то така
система
рівнянь називається нормальною.
Розв’язком системи називається сукупність функцій
y
1
,y
2,
…,y
n
, які перетворюють кожне рівняння системи в тотожність
відносно
x.
Задача Коші для системи (7.38) полягає у знаходженні
функцій
y
1
,y
2,
…,y
n
що задовольняють систему (7.38) і заданим по-
чатковим умовам:
0nxxn20xx210xx1
y|y,...,y|y,y|y
000
===
===
. (7.39)
Інтегрування системи (7.38) роблять таким чином. Диференціюємо
по x перше рівняння системи (7.38):
.
dx
dy
y
f
...
dx
dy
y
f
x
f
dx
yd
n
n
11
1
11
2
1
2
⋅
∂
∂
++⋅
∂
∂
+
∂
∂
=
Замінимо похідні
dx
dy
,...,
dx
dy
,
dx
dy
n21
їх виразами
n21
f,...,f,f із
рівнянь системи (7.38), одержимо рівняння
)y,...,y,x(F
dx
yd
n12
2
1
2
=
.
Диференціюємо одержане рівняння і, підставивши в цю
рівність значення похідних із системи (7.38), знайдемо
)y,...,y,x(F
dx
yd
n13
3
1
3
=
.
Продовжуючи далі таким чином , одержимо
)y,...,y,x(F
dx
yd
n1
n
1
n
=
.
В результаті дістаємо таку систему рівнянь:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
=
=
=
).y,...,y,x(F
dx
yd
....................................
),y,...,y,x(F
dx
yd
),y,...,y,x(f
dx
dy
n1n
n
1
n
n12
2
1
2
n11
1
(7.40)
389
З перших
(n-1) рівнянь визначимо y
2
,y
3
,…,y
n
:
⎪
⎪
⎩
⎪
⎪
⎨
⎧
′
ϕ=
′
ϕ=
′
ϕ=
−
−
−
).y,...,y,y,x(y
...........................................
),y,...,y,y,x(y
),y,...,y,y,x(y
)1n(
111nn
)1n(
11133
)1n(
11122
(7.41)
і підставимо їх значення в останнє рівняння системи (7.40) для ви-
значення
:y
1
)y,...,y,y,x(Ф
dx
yd
)1n(
111
n
1
n
−
′
=
.
Звідки
y
1
=Ψ(x,C
1
,C
2
,…,C
n
), (7.42)
де
C
1
,C
2
,…,C
n
- довільні сталі.
Продиференціюємо цей вираз
(n-1) раз, визначимо
1n
1
)1n(
2
1
2
1
dx
yd
,...,
dx
yd
,
dx
dy
−
−
як функції від x,C
1
,C
2
,…,C
n
. Підставимо ці
функції в (7.41), знайдемо
⎪
⎩
⎪
⎨
⎧
ψ=
ψ=
).С,...,С,С,x(y
.....................................
),
С,...,С,С,x(y
n21nn
n2122
(7.43)
Для того, щоб одержаний розв’язок задовольняв заданим по-
чатковим умовам, залишається лише знайти значення довільних
сталих із рівнянь (7.42) і (7.43) так, як ми це робили для одного ди-
ференціального рівняння.
Приклад
1. Проінтегрувати систему
⎪
⎩
⎪
⎨
⎧
+−−=
++=
,x2z3y4
dx
dz
,xzy
dx
dy
коли задані початкові умови
.0|z,1|y
0x0x
==
==
Розв’язування. Диференціюємо по
x
перше рівняння, маємо:
1
dx
dz
dx
dy
dx
yd
2
2
++=
. Підставляємо сюди значення
dx
dy
і
dx
dz
із систе-
ми , одержимо
;1)x2z3y4()xzy(
dx
yd
2
2
++−−+++=

390
.1x3z2y3
dx
yd
2
2
++−−=
З першого рівняння системи знайдемо
xy
dx
dy
z −−= і підста-
вимо в одержане нами рівняння:
1x3)xy
dx
dy
(2y3
dx
yd
2
2
++−−−−=
або
1x5y
dx
dy
2
dx
yd
2
2
+=++
.
Загальним розв’язком цього рівняння є
9x5e)xСС(y
x
21
−++=
−
(*)
і тоді
14x6e)xС2С2С(z
x
212
+−+−=
−
(**)
Підберемо сталі
1
С
і
2
С
так, щоб виконувались початкові
умови. На основі (*) та (**) маємо:
;9С1
1
−= ,14С2С0
12
+−=
звідки
,10С
1
= .6С
2
=
Таким чином, розв’язок системи, який задовольняє заданим
початковим умовам буде:
.14x6e)x1214(z,9x5e)x610(y
xx
+−−−=−++=
−−
4.2. Системи лінійних диференціальних рівнянь із
сталими коефіцієнтами
Система диференціальних рівнянь:
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+++=
+++=
+++=
,xa...xaxa
dt
dx
................................................
,xa...xaxa
dt
dx
,xa...xaxa
dt
dx
nnn22n11n
n
nn2222121
2
nn1212111
1
(7.44)
де коефіцієнти
a
ij
- сталі числа, t- незалежна змінна, x
1
(t),…,x
n
(t)-
невідомі функції, називається
системою лінійних однорідних ди-
ференціальних рівнянь із сталими коефіцієнтами.
Цю систему можна розв’язувати шляхом зведення до одного
рівняння
n - го порядку, як це було показано вище. Але цю систему
можна розв’язати і іншим методом. Покажемо як це робиться.
Будемо шукати розв’язок системи (7.44) у вигляді:
,ex
kt
11
α=
kt
22
ex α=
,...,
.ex
kt
nn
α=
(7.45)
