Шинкарик М.І. Вища математика
Подождите немного. Документ загружается.

401
Отже, ціна не підлягає зміні.
Взагалі кажучи, функція пропозиції – зростаюча, а тому
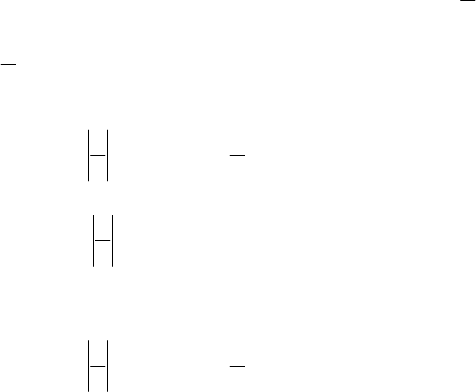
;0b >
а функція попиту – спадна, і тому
.0a <
Звідки
.0
a
b
<
Знак
виразу
t
a
b
⎟
⎠
⎞
⎜
⎝
⎛
залежить від номера року
t
, отже, ціна коливається.
Тут мають місце три випадки:
1) Якщо
,1
a
b
< то 0
a
b
lim
t
t
=
⎟
⎠
⎞
⎜
⎝
⎛
∞→
і відповідно .0plim
t
t
=
∞→
Тоді кажуть, що коливання ціни стримується.
2) Якщо
,1
a
b
= то послідовні коливання ціни складають
,000
p,p,p −
...
В цьому випадку кажуть, що коливання ціни періодичні.
3) Якщо
,1
a
b
> то ∞=
⎟
⎠
⎞
⎜
⎝
⎛
∞→
t
t
a
b
lim
і
t
p безмежно росте.
Кажуть, що коливання ціни зростає.

402
Розділ 8. РЯДИ
Поняття суми скінченої кількості чисел і її властивості відомі
ще з давніх часів. Шукаючи суму геометричної прогресії, математик
і механік Стародавньої Греції Архімед зустрівся з нескінченними
рядами.
Для детального вивчення функції рядами систематично кори-
стувались англійський математик, механік, фізик, астроном
І.Ньютон та великі німецькі вчені Г.Лейбніц
і К. Гаусс.
Однак точна теорія рядів, в основі якої лежали поняття
границі послідовності, була побудована на початку 19 ст. французь-
ким математиком О.Коші. З цього часу ряди стали основним джере-
лом дослідження в математиці. З’явились цілі розділи математики,
повністю побудовані на теорії рядів.
Методи цього розділу застосовуються для знаходження
на-
ближених значень інтегралів, які часто зустрічаються в теорії
ймовірностей та у страховій справі, і не можуть бути виражені еле-
ментарними функціями; при розв’язуванні диференціальних
рівнянь; при знаходженні наближених значень функцій, які викори-
стовуються при розв’язуванні економічних задач.
§1. Числовий ряд та його збіжність.
Ряд геометричної прогресії
Нехай задана нескінченна послідовність чисел
n321
u,...,u,u,u
....
Означення. Нескінченна сума чисел виду
...u...uuu
n321
+++++
називається числовим рядом, а
n321
u,...,u,u,u - членами ряду.
Коротко ряд записується так:
∑
∞
=
1n
n
u . Вираз для −
n
го члена
ряду при довільному натуральному
n
, називається загальним чле-
ном цього ряду і позначається
.n
u
Ряд вважається заданим, якщо відомо правило , за яким для
довільного номера
n
можна записати відповідний член ряду. За-
гальний член ряду можна задати формулою
u
n
=f(n), з допомогою
якої записується довільний член ряду.
403
Наприклад, якщо
n
n
3
1
u =
, то ряд матиме відповідно вигляд
...
3
1
...
3
1
3
1
3
1
n32
+++++ .
Якщо ряд записано у вигляді
∑
∞
=
1n
n
u , то легко записати
декілька його членів.
Наприклад, якщо задано ряд
∑
∞
=
⎟
⎠
⎞
⎜
⎝
⎛
0n
n
4
5
, то в іншій формі він
матиме вигляд
....
4
5
...
4
5
4
5
1
n2
+
⎟
⎠
⎞
⎜
⎝
⎛
++
⎟
⎠
⎞
⎜
⎝
⎛
++
Якщо відомо декілька членів числового ряду, то зрозумівши
закономірність їх утворення, можна записати загальний член ряду.
Наприклад, задано чотири перших члени ряду
...
10
4
10
3
10
2
1
32
++++ .
Як бачимо, чисельники кожного члена ряду є натуральними
числами. Знаменник першого члена ряду
10
0
=1. Кожен знаменник
наступного члена більший від попереднього в 10 разів. Таким чи-
ном, загальний член ряду записуємо
1n
n
10
n
u
−
= .
Нехай задано ряд
....u...uu
n21
++++
(8.1)
Суму
n перших його членів позначимо через S
n
:
n21n
u...uuS +++=
(8.2)
і назвемо
n-ою частинною сумою ряду.
Утворимо тепер послідовність частинних сум ряду:
.u...uuS
...............................
,uuS
,uS
n21n
212
11
+++=
+=
=
Означення. Якщо при n
→∞
існує границя послідовності
частинних сум
n
S
членів даного ряду SSlim
n
n
=
∞→
, то ряд
називається збіжним, а число S - його сумою.
404
Записують це так:
....u...uuS
n21
++++= (8.3)
Якщо послідовність частинних сум
n
S
не має границі, то
ряд називається розбіжним.
Ряд може розбігатися у двох випадках:
1)
∞=
∞→
n
n
Slim ;
2) Послідовність
n
S коливається.
Як приклад розглянемо ряд нескінченної геометричної
прогресії:
....aq...aqaqa
n2
+++++
(8.4)
Сума
n
перших членів прогресії рівна
.a
1q
1q
S
n
n
−
−
=
Якщо
1q < , то
0qlim
n
n
=
∞→
і тому
aSlim
n
n
=
∞→
.
q1
a
1q
1q
lim
n
n
−
=
−
−
∞→
Отже, якщо
1q <
,то нескінченна геометрична прогресія
утворює збіжний ряд, сума якого
.
q1
a
S
−
=
Якщо
1q >
, то ,qlim
n
n
∞=
∞→
тому
∞=
∞→
n
n
Slim
, і ряд
геометричної прогресії розбігається.
При
1q =
одержимо ряд
)0a...(aaaa ≠++++
, який має
частинну суму
naS
n
=
і .nalimSlim
n
n
n
∞==
∞→∞→
Якщо
1q −= , одержимо ряд
...
a
a
a
a
+−+−
Його частинні суми набирають таких значень:
,aS
1
=
,0S
2
=
,aS
3
= ,...0S
4
= , тобто −
n
S коливна послідовність, яка не має
границі.
Наслідок
. Якщо ряд (8.1) збігається, то різниця між сумою
S
і
частинною сумою
n
S його
...uuSSR
2n1nnn
++=−=
++
(8.5)
називається
n
-им залишком ряду.

405
Залишок R
n
ряду являє собою ту похибку, яка одержиться,
якщо замість наближеного значення суми ряду
S взяти суму S
n
пер-
ших
n членів цього ряду. Але оскільки S є границя змінної S
n
, то
очевидно ,
.0)SS(limRlim
n
n
n
n
=−=
∞→∞→
А тому, взявши достатньо велике число членів збіжного ряду,
можна суму цього ряду обчислити з любою точністю.
Звідси випливає, що основною задачею теорії рядів є
дослідження збіжності ряду.
В наступному прикладі покажемо застосування ряду
нескінченно спадної геометричної прогресії в економічних
дослідженнях.
Приклад
. Нехай I
0
- початкові інвестиції, вкладені в замкнуту
економічну систему, а
q- доля національного доходу, яка йде на
споживання, то в моделі Кейнса
[]
23
вартість національного при-
бутку
Y
виражається формулою
0
I
q1
1
Y
−
=
. (8.6)
Права частина рівності (8.6) є не що інше як сума ряду
нескінченно спадної геометричної прогресії із знаменником
1q <
і
0
n2
I...)q...qq1(Y +++++= . (8.7)
Ця формула може бути використана для знаходження зміни
вартості національного прибутку в залежності від початкових
інвестицій
0
I та її долі
q
, що йде на споживання.
§2. Гармонічний ряд
Ряд ...
n
1
...
3
1
2
1
1 +++++ (8.8)
називається
гармонічним.
Доведемо розбіжність цього ряду. Скористаємося тим, що
змінна
n
n
n
1
1x
⎟
⎠
⎞
⎜
⎝
⎛
+= при необмеженому зростанні n прямує до не-
перового числа
e, залишаючись меншим своєї границі. Тому при
любому цілому додатному
n
маємо
n
n
1
1e
⎟
⎠
⎞
⎜
⎝
⎛
+> .

406
Звідси
,
n
1
1lnneln
⎟
⎠
⎞
⎜
⎝
⎛
+>
або
,
n
1
1lnn1
⎟
⎠
⎞
⎜
⎝
⎛
+>
або .
n
1n
ln
n
1 +
>
Підставляючи в останню нерівність замість
n
числа 1,2,3,...
одержимо нерівності:
.nln)1nln(
n
1
.......................
,3ln4ln
3
1
,2ln3ln
2
1
,
1
ln
2
ln
1
−+>
−>
−>
−>
Додавши почленно ці нерівності, одержимо
)1nln(
n
1
...
3
1
2
1
1 +>++++ або ).1nln(S
n
+>
Але ,)1nln(lim
n
∞=+
∞→
а тому і ;Slim
n
n
∞=
∞→
тобто ряд (8.8)
розбігається.
§3.
Необхідна ознака збіжності числового ряду
ТЕОРЕМА. Якщо ряд
...u...uuu
n321
+++++ (8.9),
збігається, то його
n
-ий член
n
u при необмеженому зростанні
номера
n
прямує до нуля.
Доведення. Ми маємо
1n3211n
u...uuuS
−−
++++= і
n1n321n
uu...uuuS +++++=
−
. Звідси
1nnn
SSu
−
−=
. Оскільки
даний ряд збігається, то
SSlim
n
n
=
∞→
і
SSlim
1n
n
=
−
∞→
. Звідси
,0SSSlimSlim)SS(limulim
1n
n
n
n
1nn
n
n
n
=−=−=−=
−
∞→∞→
−
∞→∞→
що і
потрібно було довести.
Приклад
. Дослідити збіжність числового ряду
...
2n100
n5
...
302
15
202
10
102
5
+
+
++++
.
407
Розв’язування. Загальний член ряду .
2n100
n5
u
n
+
=
Знайдемо
при
∞→
n
його границю :
.0
20
1
n
2
100
5
lim
2n100
n5
lim
nn
≠=
+
=
+
∞→∞→
Отже, даний ряд є розбіжним.
Відмітимо, що
0ulim
n
n
=
∞→
є лише необхідною умовою
збіжності числового ряду, але не достатньою. Це означає, що дана
умова може виконуватися, але відповідний числовий ряд може бути
розбіжним.
Прикладом є
гармонічний ряд ...
n
1
....
4
1
3
1
2
1
1 ++++++ .
Як бачимо, необхідна умова для цього ряду виконується:
0
n
1
limulim
n
n
n
==
∞→∞→
, однак він є розбіжним .
Існує декілька ознак, які дозволяють стверджувати збіжність
або розбіжність числових рядів.
§4.
Достатні ознаки збіжності числових рядів
з додатними членами
4.1.
Ознака порівняння рядів
ТЕОРЕМА. Якщо кожний член ряду
...u...uu
n21
++++ (8.10)
з
додатними членами менший (або рівний) відповідного члена
збіжного ряду
...v...vv
n21
++++ (8.11)
з
додатними членами, то ряд (8.10) збігається.
Якщо кожний член ряду (8.10) більший (або рівний)
відповідного члена розбіжного ряду (8.11), то ряд (8.10)
розбігається.
Доведення. Нехай
nn
vu ≤ і ряд (8.11) збігається. Складемо су-
ми перших
n
членів рядів (8.10) і (8.11):
408
,u...uuS
n21
)1(
n
+++=
.v...vvS
n21
)2(
n
+++=
Оскільки
,...,vu,...,vu,vu
nn2211
≤≤≤ то .SS
)2(
n
)1(
n
≤
Ряд (8.11) збігається, то
.SSlim
)2()2(
n
n
=
∞→
Звідси випливає, що
.SS
)2()1(
n
< При необмеженому зростанні номера
n
послідовність
сум
),,..,3,2,1n(S
)1(
n
= як зростаюча послідовність і обмежена звер-
ху числом
)2(
S , має границю ,SS
)2()1(
≤ тобто
,SSSlim
)2()1()1(
n
n
≤=
∞→
а тому ряд (8.10) також збігається.
Нехай
nn
vu ≥
і ряд (8.11) розбігається. Тоді в силу
нерівностей
nn2211
vu,...,vu,vu ≥≥≥ випливає, що .SS
)2(
n
)1(
n
≥ Але
оскільки
,Slim
)2(
n
n
∞=
∞→
то
)1(
n
S також буде необмежено зростати ,
тобто ряд буде розбігатися.
Приклад 1. Дослідити збіжність ряду
...
3n
1
...
34
1
33
1
3
1
1
1n32
+
⋅
++
⋅
+
⋅
++
−
Розв
’язування. Порівняємо даний ряд з нескінченно спадною
геометричною прогресією
...
3
1
...
3
1
3
1
1
1n2
+++++
−
Оскільки
1n1n
3
1
3n
1
−−
≤
⋅
для довільного
n
, а ряд нескінченно
спадної геометричної прогресії є збіжним рядом, то згідно з озна-
кою порівняння рядів вихідний ряд буде збіжним.
Приклад
2. Дослідити збіжність ряду
...
n
1
...
3
1
2
1
1
+++++
Розв
’язування. Даний ряд порівняємо з гармонічним рядом.
Для довільного
n
виконується нерівність .
n
1
n
1
>
Як було показано вище, гармонічний ряд розбігається, отже
даний ряд розбігається також.
409
4.2. Ознака Даламбера
ТЕОРЕМА. Нехай всі члени ряду ...u...uu
n21
++++ дода-
тні і нехай при необмеженому зростанні номера
n
границя від-
ношення
−+ )1n(
го члена до
n
-го існує і дорівнює деякому чи-
слу l , тобто
l
u
u
lim
n
1n
n
=
+
∞→
.
Тоді :
1. Якщо
1l < , то ряд збіжний.
2. Якщо
1l >
, то ряд розбіжний.
3. Якщо
1l = , то ознака не дає відповіді на питання про збіж-
ність або розбіжність ряду, тобто ряд в даному випадку може як збі-
гатися , так і розбігатися.
Доведення
. Нехай маємо ряд
...u...uu
n21
++++
(8.12)
складений із додатних чисел, і нехай
l
u
u
lim
n
1n
n
=
+
∞→
. (8.13)
Тоді при достатньо великому
n, тобто при n не меншому де-
якого числа
N маємо:
ε<−
+
l
u
u
n
1n
, де ε - як завгодно мале додатне число. Звідси
ε+<<ε−
+
l
u
u
l
n
1n
як тільки Nn ≥ .
а) Нехай
l<1. Ми зможемо вибрати число ε настільки малим,
що
l+ε також буде менше одиниці, тоді, поклавши l+ε=q, одержимо:
1q0 <<
,
,q
u
u
N
1N
<
+
,q
u
u
1N
2N
<
+
+
q
u
u
2N
3N
<
+
+
і т.д.
Отже,
,...uqquu,uqquu,quu
N
3
2N3NN
2
1N2NN1N
<<<<<
+++++
.
Звідси випливає, що члени ряду
....uu
2N1N
++
++
., які пред-
ставляють
N- ий залишок ряду (8.12), менші відповідних членів не-
скінченно спадної геометричної прогресії
...uquqqu
N
3
N
2
N
+++
(знаменник
)1q <
.
Цей ряд збіжний, отже ряд (8.12) збіжний.

410
б) Нехай 1l > . Тоді можна підібрати
N
таким, що при Nn ≥
буде справедлива нерівність
ql
u
u
n
1n
=ε−>
+
. (8.14)
де
ε
вибирається настільки малим, щоб величина ε−= lq залиша-
лась більшою 1. Тоді кожний наступний член ряду буде більшим за
попередній, а це суперечить необхідній ознаці збіжності ряду.
Отже, ряд розбігається.
в) В тому випадку, коли границя
l=1, ознака Даламбера не дає
відповіді на питання про збіжність чи розбіжність ряду. Ряди мо-
жуть бути як збіжними так і розбіжними.
Приклад
1. Дослідити збіжність ряду
...
!n
2
...
!4
8
!3
4
!2
2
1
1n
++++++
−
.
Розв
’язування. Оскільки
!n
2
u
1n
n
−
=
, то
)!1n(
2
u
n
1n
+
=
+
, а зна-
чить,
.0
1n
1
lim2
)!1n(
!n2
lim
)!1n(2
!n2
lim
!n
2
:
)!1n(
2
lim
u
u
liml
nn
1n
n
n
1nn
n
n
1n
n
=
+
=
+
=
=
+
=
+
==
∞→∞→
−
∞→
−
∞→
+
∞→
Тут
;n...321!n ⋅⋅⋅⋅= ;1!1!0 ==
!n)1n()!1n( +=+
Оскільки
10l <= , то згідно з ознакою Даламбера даний ряд
збігається.
Приклад
2. Дослідити збіжність ряду
...
10
!n
...
10
321
10
21
10
1
n32
+++
⋅⋅
+
⋅
+ .
Розв
’язування. Тут
n
n
10
!n
u =
,
1n
1n
10
)!1n(
u
+
+
+
=
.
Тому
.
10
1n
lim
1010!n
10!n)1n(
lim
10!n
10)!1n(
lim
u
u
liml
n
n
n
n
1n
n
n
n
1n
n
∞=
+
=
⋅
+
=
+
==
∞→∞→
+
∞→
+
∞→
Оскільки
l=∞, то за ознакою Даламбера числовий ряд розбігається.
