Smith G.T. Cutting Tool Technology: Industrial Handbook

Подождите немного. Документ загружается.

trated in Fig. 155. In these diagrams a simplistic repre-

sentation for a range of cutting insert proles is shown

and for clarity, the tangential force has been excluded,

with just the axial and radial force components indi-

cated for each type of cutting insert shape. Assuming

that the overall cutting data is identical in each case

(i.e. the same: rotational speed, feedrate, D

, insert

rake angle, plus workpiece material), then the only

variable in the longitudinal turning process here will

be the cutting insert shape its orientation. e com-

ponent cutting forces – axial and radial, will vary for

each tool prole in their respective magnitudes, due

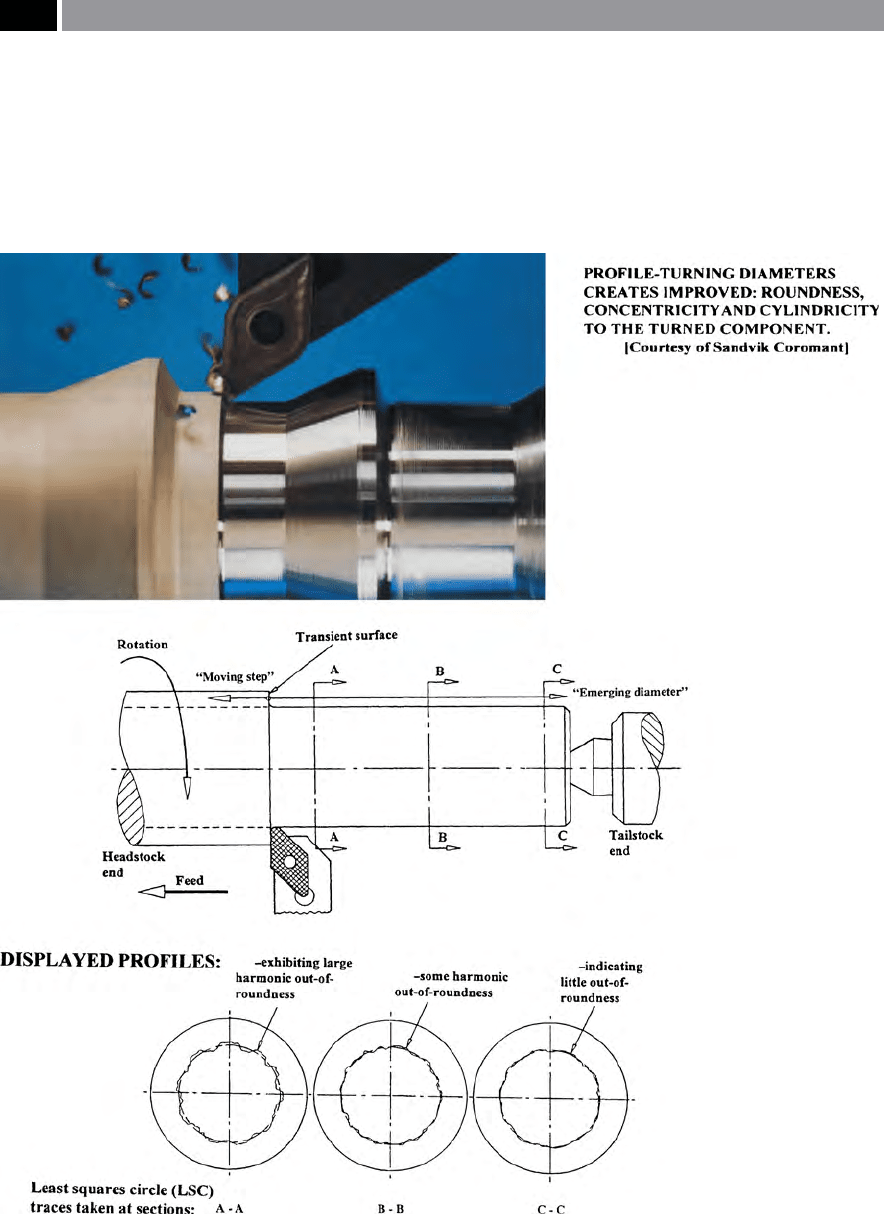
Figure 154. Machined roundness is inuenced by a number of factors: unbalanced cutting forces, non-integral headstock and

lack of support on slender/long workpieces

292 Chapter 7

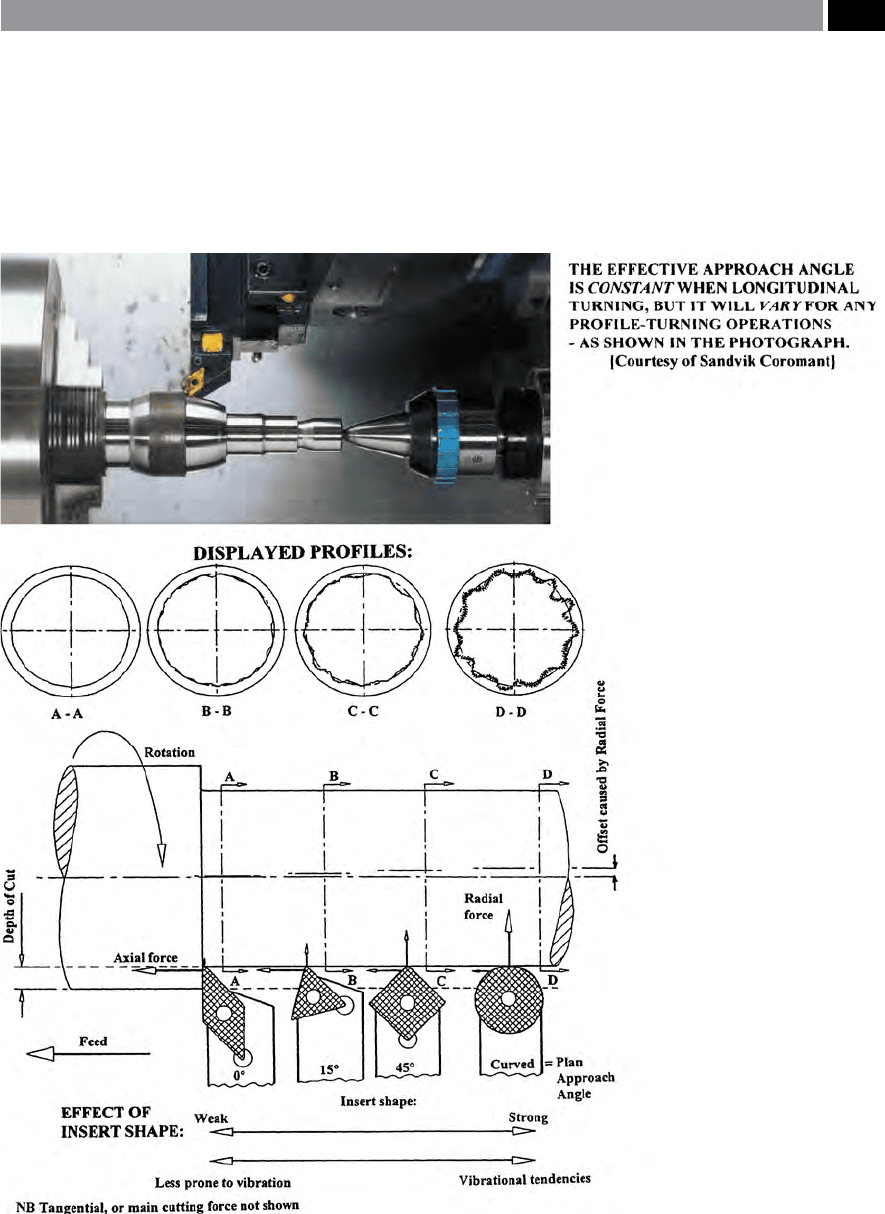
to the variation in plan approach angles. In the case of

the orthogonal insert (0°) plan approach angle, the ax-

ial force dominates with virtually no radial force com-

ponent present, this axial force being directly linked

with the feedrate. e displayed prole chart for this

harmonic roundness trace (i.e. section on ‘A-A’), for

the 0° plan approach angle, shows virtually negligible

harmonic eects. If a triangular-shaped cutting insert

geometry was selected, in this case having an 15° plan

approach, here there is a slight reduction in the axial

force component and a corresponding increase in its

radial counterpart. is slight increase in the radial

Figure 155. Turned roundness can be signicantly aected by the insert shape, its approach angle – which aects cutting forces

– resulting in harmonic out-of-roundness

Machinability and Surface Integrity 293

force, in combination with a marginally longer cut-

ting edge being in contact with the workpiece’s ‘tran-

ent surface’

, leads to a slight increase in the har-

monics on the displayed prole chart (‘B-B’). As the

bliquity of the insert’s plan approach angle increases,

as depicted by the square-shaped cutting insert, being

inclined at an angle of 45°, then the axial and radial

force components equalise. Here, the considerable

radial force component has a signicant eect on the

displayed prole trace, as illustrated by the section at

‘

C-C’ , where the harmonics have increased, but with a

notable vibrational tendency superimposed onto this

primary harmonic. is increase in vibration during

turning, is the result of two noteworthy factors: rstly,

the length of the transient surface has increased – with

this square insert’s greater plan approach angle; sec-

ondly, as a result of this rst condition of increased

obliquity, the radial force aects workpiece rigid-

ity, which is compromised, leading to an exacerbated

turned part surface roundness and accompanying

chatter-marks.

Finally, when turning with a round insert geometry,

this will lead to a vast increase in the radial force com-

ponent, which in turn may cause signicant harmonic

out-of-roundness, if a very rigid set-up is not utilised.

In this case, the round insert’s displayed prole trace,

shows evidence of a signicant increase in vibration

– chatter – present, which has a dramatic eect on

the prole of primary harmonic (section on ‘D-D’)

– more will be said on the subject of ‘chatter-marks’ on

the component’s surface shortly. e rationale for this

notable harmonic amplication when using round in-

serts is the product of several interrelated factors. e

transient surface in contact with the round/curved

prole has been markedly increased, together with the

plan approach at the tangency position – with respect

to the workpiece – being at a maximum; thus, the

combination these two factors leads to a momentous

deterioration in workpiece rigidity and as a result here,

the vibration will especially increase.

26 ‘Transient surface’ , can be dened as: ‘e part of the surface

formed on the workpiece by the cutting edge and removed dur-

ing the following cutting stroke, [by the next] revolution of the

tool, or workpiece’ (Boothroyd, 1975).

NB In the case thread-turning operations, the transient ank’s

surface only remains until the next pass of the screw-cutting

insert obliterates it, or until the nal thread depth is reached.

If a large volume of workpiece stock has to be re-

moved in a series of roughing cuts, a strong insert is

necessary, therefore the problem associated with the

harmonic behaviour of cutting insert geometry be-

comes of less importance. is latter fact allows either

a square, or round cutting insert to be utilised due to

their intrinsic strength and if vibration is a problem,

then a ‘nishing cut’ with an insert having an 0° plan

approach geometry would remove any probable sur-

face chatter-marks.

e case of turning with a round insert geometry is

worthy of a closer investigation, as several factors in-

uence the harmonic roundness of a workpiece turned

with its curved prole. For example, let us consider

several conditions for employing a standardised round

insert and its subsequent aect on the harmonics of

the turned part. If one assumes that an identical: ro-

tational speed, feedrate and workpiece material was

used, but having diering D

’s – to isolate variabil-

ity in the turning process. In the rst example using a

small D

, the radial force component is large in com-

parison to the axial force, but the harmonic workpiece

roundness is not compromised here – as these forces

are minute. Conversely, an extreme example of using

a round insert might be when employing a larger D

Here, the radial force component has been reduced

in comparison to the axial component, although the

magnitude of these forces will be considerably greater

than in the former case. e pressure exerted on the

very long contact region at the transient curved sur-

face, creates potential harmonics in the turned part as

the resultant force has now signicantly increased. So,

the inuence of an increased D

, in combination with

the round insert prole can create a very long contact

region at the transient surface, thereby causing un-

wanted harmonic eects on the turned surface.

In Appendix 9, a visual impression is given of the

principal techniques for roundness measurement and

its assessment, together with some of the ltering ef-

fects are highlighted.

7.3 Chatter in Machining

Operations

In the machining of metals, chatter (Fig. 156) is a form

of self-excited vibration introduced by the closed-loop

force-displacement response to cutting. e plastic de-

formation during machining operations is always pro-

294 Chapter 7

ceeded by elastic deformation – the situation is akin to

that of it acting somewhat like a ‘big spring’

. More-

over, the mechanism by which a cutting process dissi-

pates energy is termed chatter and vibration, also this

being a function of the workpiece’s rotational speed.

Any chatter/vibration can clearly be heard as an un-

wanted machining noise by an experienced machinist,

who would then modify the speed accordingly. ere

are a wide variety of causes for chatter, including the

process-induced eects from the cutting forces, which

may be the result of changes in: the cutting velocity;

chip cross-sectional area; tool/chip interface friction;

BUE, variations in the workpiece composition; or the

most common factor being process modulation result-

ing in regeneration of vibration. If greater energy is

input into the dynamic ‘machining-loop’ than can be

readily dissipated by the following: mechanical work;

damping, or friction, then an ‘equilibrium status’ is re-

quired and this output is via the somewhat superu-

ous eect of the generation of chatter/vibration.

Vibration is a debilitating process aecting both the

machined surfaces and reducing tool life in any ma-

chining operation, consequently it must be appropri-

ately identied – classied, then one has the potential

to nd the actual cause of this unwanted eect and

resolve it accordingly. In essence, in machining opera-

tions there are three types of vibration that may tran-

spire, these are:

•

Free vibration – this being the response to sudden

change, or to any initial condition, where the vibra-

tional amplitude decreases with time, occurring at

the system’s natural frequency,

An interrupted machining operation, or work-

piece feature can create this vibrational eect and it

frequently appears as shadows, or lines following a

surface discontinuity.

•

Forced vibration – can be regarded as a response to

a periodic – repetitive timing – input that occurs at

an identical frequency. At this point, the vibrational

27 ‘Spring-cuts’ , are always present in any ductile component

machining operation, resulting from the relaxation of the

forces and the elastic recovery of the tool and workpiece aer

the cutting insert’s passage along the part. In fact, if the tool

is repositioned once more at the beginning of the original cut,

then simply fed along the component, it will take a minute cut

– assuming that the tool’s edge is still suciently sharp, this is

termed the ‘spring-cut’.

amplitude stays constant for a set of input condi-

tions, being non-linearly related to speed.

NB 

e most common examples of this eect are

caused by: cutter imbalance, cutting teeth impact-

ing on workpiece, tooling misalignments, plus the

occurrence of any form of rotational system reso-

nance.

•

Self-excitation vibration, or chatter – occurs

through the system’s periodic response to a con-

stant input, which may intensify in amplitude – be-

coming unstable, oen occurring – regardless of

the input, but close to the natural frequency of the

system.

Chatter is due to waviness regeneration in

the machined surface, it commonly occurs during

metal cutting operations (i.e. see Fig. 156a).

What is chatter and how might can be characterised?

Degarmo, et al. (2003), has produced a list of the fol-

lowing factors that can indicate the onset of chatter,

these being characterised by:

•

Sudden onset of vibration – whose amplitude will

rapidly increase until a maximum threshold – sat-

uration – is reached (i.e sounding like either: a

screech, whine, or buzz),

•

Chatter frequency is near to that of the machin-

ing system’s natural frequency (i.e critical fre-

quency) – changing only slightly with any process

parameter variations. e largest force-displace-

ment response occurs at ‘

resonance’

enabling the

maximum dissipation of energy,

•

Chatter produces unacceptable surface texture

(Fig. 156a) – normally highlighted by either an an-

gular, or helical pattern (i.e. the visual appearance

28 ‘Resonance’ , is of practical importance in many engineering

applications, because relatively few oscillatory forces can re-

sult in large vibrational amplitudes that can cause damage, or

interfere with the functioning of the system.

NB e classic example of this phenomenon was found when

ranks of soldiers marched across a bridge in unison (i.e. ‘in-

step’) which, if it coincided with one of the bridge’s resonant

frequencies, could create damage to the structure – despite the

fact that the bridge could safely support their overall weight.

Hence, the order to ‘break-rank’ (i.e randomising both their

pacing and steps) when proceeding over a structure such as a

bridge was mandatory.

Machinability and Surface Integrity 295

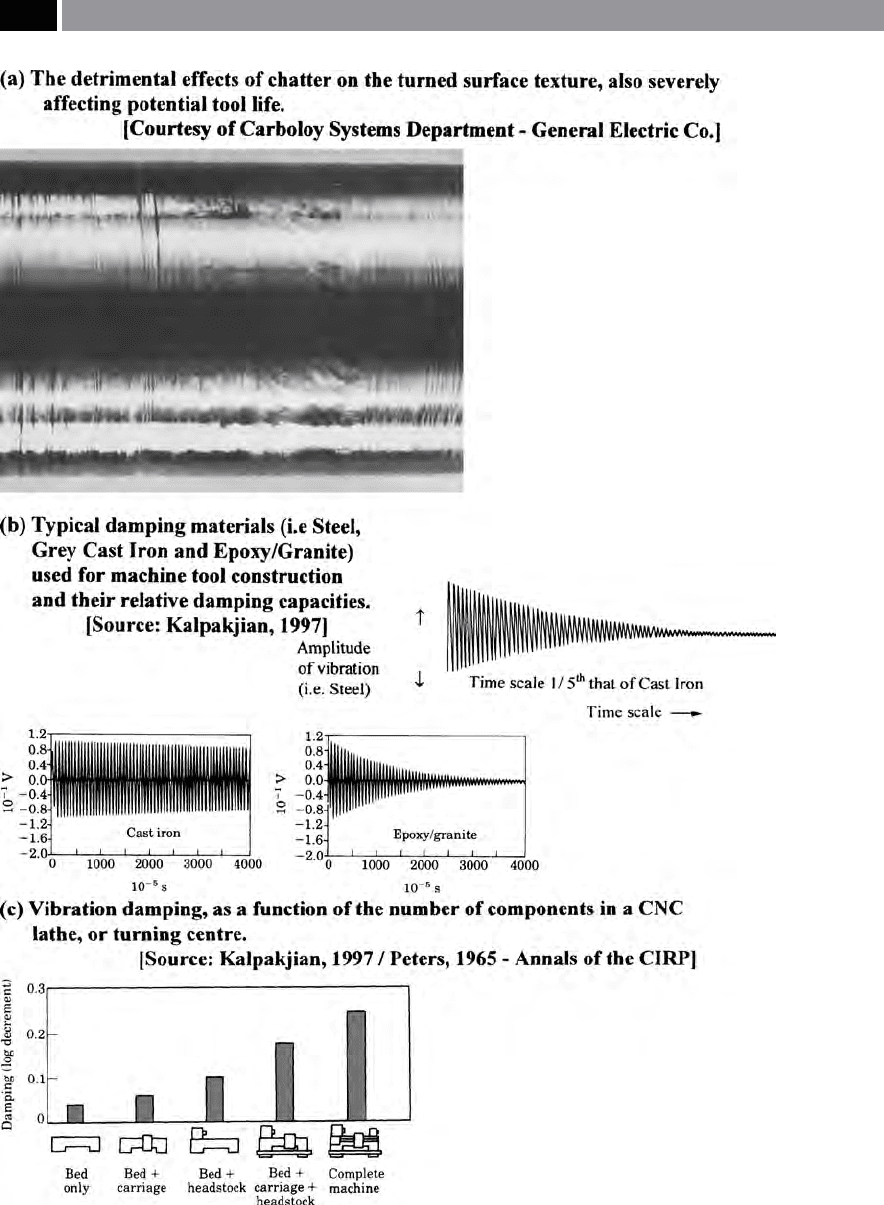
Figure 156. Vibration and chatter in machining operations, with their machine tool damping characteristics.

296 Chapter 7

is either ‘pearled’ , or ‘sh-scaled’) superimposed

over the normal cutting insert’s feed marks,

•

Visible surface undulations – these eects are re-

produced in the direction of feed, being the prod-

uct of either serrated, or wavy chip formations, of

variable thicknesses.

7.3.1 Chatter and Chip Formation –

Significant Factors Influencing

its Generation

e stability of the cutting process and the onset of re-

generative chatter is inuenced by a range of factors,

such as the: cutting stiness (K

)

of the workpiece

material – related to its machinability; parameters

of the machining process (e.g. speed, feed, D

, chip

width – total); insert cutting geometry (e.g. rake and

clearance angles, edge preparation, insert shape and

size); cutting process dynamic characteristics (e.g.

machine-tooling-workpiece/xturing). Hence, during

machining operations on the workpiece, the chip is

formed by shearing over the chip area, producing the

cutting, or tangential force (F

). e magnitude of this

tangential force is heavily inuenced by the product

of the workpiece material’s stiness (K

) and the chip

area, as follows:

= K

× t × w

Where:

= tangential force (N),

= workpiece material’s stiness (N mm

–2

t =

chip thickness (mm),

w =

chip width (mm).

e direction of the tangential force (F

) is predomi-

nantly aected by the cutting insert’s rake and clear-

ance angles, together with the edge preparation on the

insert. In many single-/multi-point machining opera-

tions used to generate for example a milled surface,

there is a requirement to overlap the adjacent cutting

paths (Fig. 84c). For most single-point machining op-

29 ‘Cutting stiness’ (K

), is closely associated with that of ‘ow

stress’*, but is more simple to calculate and can be thought

of as a workpiece material property, being dependent on its

hardness.

*‘Flow stress’ , can be dened as: ‘e stress required to sustain

plastic deformation at a particular strain’ ( Kalpakjian, 1997).

erations, this former over-lapping of tool paths does

not take place in the same manner, but will only occur

aer one complete revolution of either the workpiece,

or tool. In operations by either milling (Fig. 85), or

drilling (Fig. 50), an overlap takes place in a fraction

of a revolution, this being dependent upon how many

cutting edges are present on the tool.

In the Degarmo, et al. (2003) machining model

shown in (Fig. 157a), the cutting or tangential force

)

generation may cause a relative displacement ‘X’

between the cutting insert and the workpiece, aecting

the uncut chip thickness (t), this results in changing

the cutting force. is coupled relationship between

displacement in the ‘Y’ direction – modulation direc-

tion – and the resultant cutting force, creates a closed-

loop response system. Here, the modulation direction

is normally at 90° to the machined surface, so denes

the chip thickness. As a consequence of these inter-

related factors, there is a phase-shi (ε) between the

subsequent overlapping machined surfaces, resulting

in a variable chip thickness and modulation of the

displacement, causing chatter vibration to take place.

Accordingly, this phase-shi between overlapping cut-

ting paths is accountable for the production of chatter

(Fig. 157b). Moreover, there is a favoured speed cor-

responding to a phase-locked condition (e.g. when

‘ε=0’), resulting in a constant chip thickness (t). By

obtaining a constant chip thickness, this results in a

‘steady-state’ cutting force generation with it and, the

eradication of the feed-back mechanism for regenera-

tive chatter. In essence, this is the goal for all machin-

ing operators, as they attempt to achieve this eect by

vary the cutting speeds for a given set of conditions for

a particular machining operation.

7.3.2 Chatter – Important Factors

Affecting its Generation

In the previous sections, a brief discussion was made

concerning just some of the causes of regenerative

chatter mechanisms. It is worth looking in greater de-

tail at the reasons why this superuous chatter occurs,

explaining how and why it is generated in the hope of

30 In the Degarmo, et al. (2003) model diagrammatically shown

in Fig. 157a, they use the term and nomenclature of: ‘cutting

force’ and ‘F

’ , whereas previously in the text, this has been

referred to as the ‘tangential force’ , denoted by ‘F

’.

Machinability and Surface Integrity 297

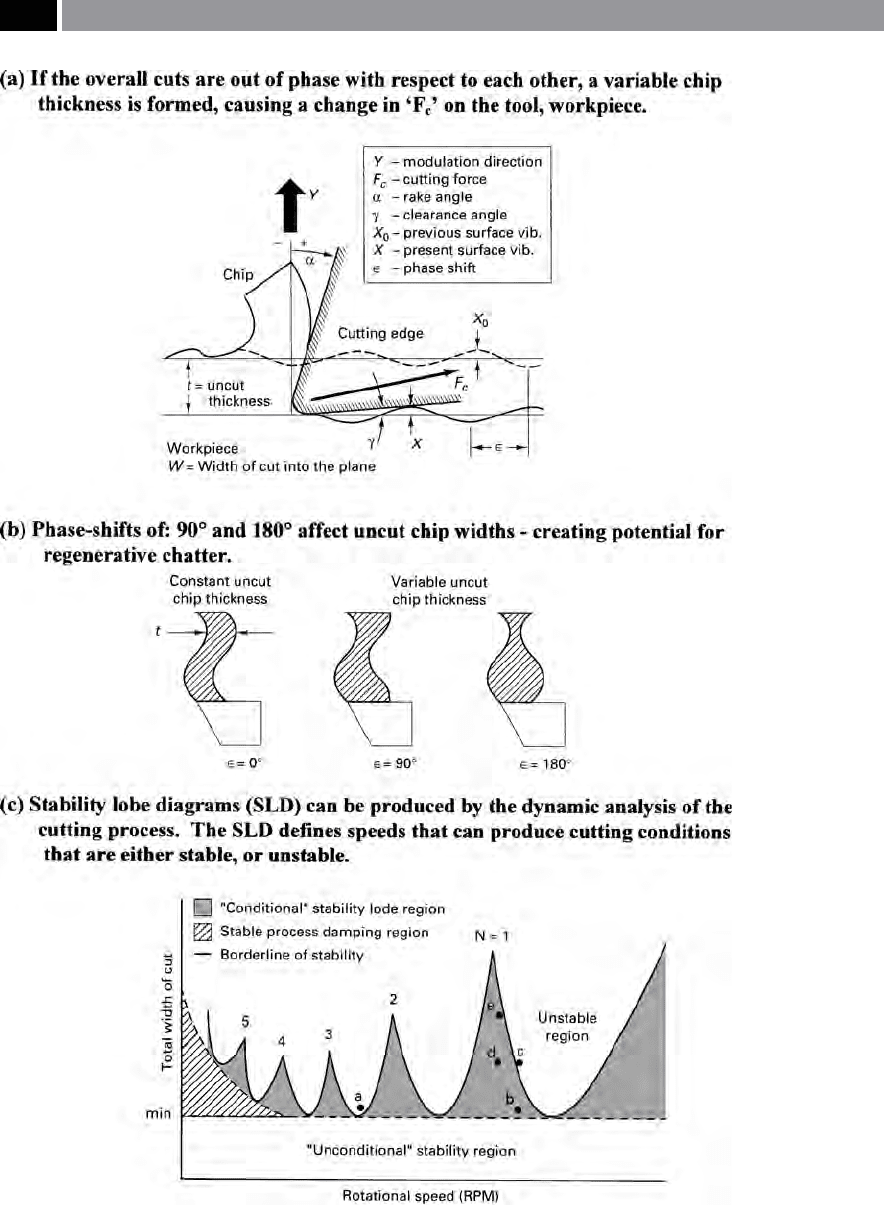
Figure 157. A chatter model, with potential chatter conditions and the application of the ‘stability lobe

diagram’. [Source: Degarmo, Black & Kosher, 2003]

298 Chapter 7

either entirely eliminating it, or at the very least, min-

imising its aect on the overall machining process.

Chatter during machining can result from a range of

multifarious and oen linked-factors, they include:

•

Depth of cut (D

) – can be considered as the prin-

cipal cause and, for the prospective control of chat-

ter. e D

delineates the chip width, acting as

the feed-back gain

within the closed-loop cutting

process,

NB 

e machining processes ‘stability limit’ – be-

ing the threshold between stable cutting and chat-

ter – can be determined from trial-and-error by

simply incrementally increasing the D

until the

commencement of chatter, then‘backing-o’ at this

level. e prediction of chatter’s onset can be found

analytically, this value being based upon thorough

knowledge of material stiness and cutting system

dynamics.

•

Rotational speed – is probably the simplest param-

eter to modify, thereby altering chatter and its as-

sociated amplitude,

NB 

e peripheral speed of either the rotating

tool, or workpiece, aects the phase-shi between

overlapping surfaces and its associated vibration

regeneration.

•

Feed – for milling operations the feed per tooth de-

nes the average uncut chip thickness (t), inuenc-

ing the magnitude of the cutting process. Chatter

is not unduly aected by the feedrate selected, but

feed does have an eect on the predictable severity

of vibration during machining,

NB A

s no cutting force exists if the vibration oc-

curs in the ‘Y’ direction – resulting in loss of con-

tact between the tool and workpiece – the maxi-

mum amplitude of chatter vibration will be limited

by its feed.

31 ‘Gain’ , can be practically dened in the following way: ‘e

ratio of the magnitude of the output of a system with respect

to that of the input – the conditions of operation and measure-

ments must be specied’ (Smith, 1993, et al.).

•

Cutting stiness (K

) – is a material property con-

nected to: shear ow stress; hardness, as well as

work-hardening characteristics of the workpiece,

this factor oen being referred to in a metaphorical

sense of its material’s machinability characteristics,

NB M

aterials that might oer poorer comparative

machinability, for example titanium, require con-

siderably higher cutting forces leading to a greater

displacement in the ‘Y’ direction and as such, oer

a less stable cutting action.

•

Width of chip (total) – is equivalent to the product

of the D

multiplied by the number of cutting edges

engaged in the cut. Furthermore, the total cut width

will inuence the stability of the cutting process,

NB A

t a preset D

corresponding to that of the

‘stability limit’ , increasing the number of engaged

cutting edges, will result in chatter, or vice-versa.

•

Cutting tool geometry – inuences both the direc-

tion and the magnitude of the cutting force, in

particular the quantity of the force component in

the modulation direction ‘Y’. So, an increased force

occurring in the ‘Y’ direction, causes amplied dis-

placement and vibration at 90° to the surface, creat-

ing ideal conditions for chatter. Other cutting insert

geometrical factors that can inuence the cutting

stability include the following:

–

Back rake angle (α) – as it is inclined to a more

positive angle, the length of the commencement

of the shearing zone decreases, this in turn, re-

duces the magnitude of the cutting force (F

). As

the back rake inclination becomes larger, then

this directs the cutting force in a more tangential

manner, thereby reducing the force component

in the ‘Y’ direction – creating improved stability

at higher speeds,

NB A

n insucient feedrate in comparison to the

insert edge radius produces a less ecient cutting

action, with more tool deection and reduced ma-

chining stability.

–

Clearance angle – reduction (γ) – has the eect

of increasing the frictional contact at the inter-

face between the tool and workpiece, possibly

having a process damping eect. is potential

stabilising eect could be the result of energy

Machinability and Surface Integrity 299

dissipation – heat transformation, which could

result in decreased tool life, with the superu-

ous eect of thermal distortion of the machined

part, or an increase in the workpiece’s heat-af-

fected zone (HAZ),

NB O

n a newly-tted cutting insert, if initial wear

occurs, this can sometimes have a stabilising eect

for the onset of chatter.

–

Nose radius – size, insert shape – diamond tri-

angular, square, round, plan approach angle

– positive, neutral, negative – all inuence the

area of the chip shape and its corresponding ‘Y’

direction. e orientation of the modulation

direction ‘Y’ toward a dynamically more-rigid

direction angle, allows a decrease in vibrational

response, giving greater overall process stability

– having notably less chattering tendencies.

As machining process stability is a direct result of

characteristics of dynamic force displacement between

both the workpiece and the cutting insert, all of the

various factors of a machining system: machine tool;

spindle; tooling; workpiece; workholding – in varying

degrees, can inuence chatter. To increase process sta-

bility of the machining system, it is necessary to maxi-

mise the dynamics, this being the overall product of its

static stiness and damping capacity. Further, machin-

ing stability can be increased by utilising tooling with

the greatest possible diameter with the minimum of

tool overhang. By way of a caution concerning chatter

frequency, this normally occurs near the most exible

vibrational mode of the machining system.

7.3.3 Stability Lobe Diagrams

In Fig. 157c, a ‘Stability lobe diagram’ (SLD) is de-

picted, which relates to the: total cut width that can be

machined, to the tooling’s rotational speed, for a speci-

ed number of cutting inserts. For example referring

to the: Degarmo, et al. (2003) diagram, suppose the

total width of cut was maintained below a minimum

level

, then the process stability would exhibit ‘speed

32 If the total cut width was maintained below a minimum level,

in practical terms this would be of limited value for many ma-

chining systems.

independence’ , or an ‘unconditional stability’. Hence,

at relatively slow speeds an increased stability can

be achieved within the process damping region – as

shown. e ‘conditional stability’ lobe regions of the

diagram, permit an increased total cut width (i.e the

x number of cutting edges, these being engaged

in the cut) at dynamically preferred speeds, at which

the phase-shi ‘ε’ between overlapping, or consecutive

cutting paths approaches zero. In Fig. 157c, stability

lobe number ‘N’ refers to the complete vibration cycles

existing between overlapping surfaces. Moreover, the

higher speeds correspond to lower lobe numbers, pro-

viding the utmost potential increase in the total cut

width and material removal rate – this being due to

the greater lobe height and width. If the total cut width

exceeds the stability threshold – even assuming that

the cutting process is operating at the desired speed,

chatter will occur. So, the larger the total cut width

bove the ‘stability limit’ , the more unstable and ag-

gressive the chatter vibration becomes.

Referring to the diagrammatic representation of

the SLD on the graph in Fig. 157c, if a chatter con-

dition arises, such as that found at point ‘a’ ,

the ro-

tational speed is attuned to the initial recommended

speed (i.e. when ‘N

=1’), resulting in stable machining

at point ‘b’ on this diagram. e D

can be incremen-

tally increased until the onset of chatter again – as the

threshold stability is crossed at point ‘c’. By utilising a

hand-held ‘speed analyser’

whilst the chatter contin-

ues – under the previously-selected operating condi-

tions, this will result in the ‘analyser’ giving a modied

speed recommendation that corresponds to point ‘d’.

Now, if required, the D

can be progressively incre-

33 ‘Speed analysers’ , are normally hand-held devices that pro-

duce dynamically-favoured speed recommendations and are

commercially available. Such ‘speed analyser’* equipment

when utilised for a cutting process, can show the relative mo-

tion between the tooling and the workpiece and recommends

the appropriate speed to avoid chatter-eects.

*‘Speed analysers’ can be successfully used for many industrial

applications, such as those involving: High-speed; in-chip,

hardened-die machining; multi-point cutting operations –

milling, etc.; Turning and boring operations. ese ‘speed anal-

ysers’ can also be employed for workpiece compositions rang-

ing from ductile metals (i.e. aluminium and steel grades) and

brittle materials (i.e. cast irons and brasses, etc.), together with

some non-metallics (plastics, etc.) and composite materials

(carbon bre, etc.).

300 Chapter 7

mentally increased to point ‘e’

– this being a ‘safe-

limit’ for the optimum machining operation.

7.4 Milled Roundness –

Interpolated Diameters

Circular features such as bosses, circular rebates, etc.,

can be CNC milled by utilising a specic word-ad-

dress ‘

circular interpolation’

command. is CNC

function creates precise and accurate circular control

in two slideways simultaneously, while the milling

cutter mills around the workpiece, as depicted in Fig.

158. Here, the milling cutter’s rigidity plays an impor-

tant role in the quality of the nal machined feature,

this being based upon the ‘

rigidity square rule’

. e

deected milling cutter illustrated in Fig. 158-right,

having lack-of-rigidity will produce some unwanted

eects on the nal milled part. Cutter deection not

only introduces the potential for chatter vibration,

but if used to mill up to square shoulder, its deection

distorts the component geometry and introduces har-

monic variation to the circular interpolated feature.

So that minimal change takes place in a milled prole,

it is advisable to keep to cutter lengths having short

34 Generally-speaking, it is not advisable to attempt to maintain

both the D

and the total cut width at the stability thresh-

old , because any variation in the: workpiece aecting its cut-

ting stiness ‘K

’; speed errors; or perhaps small changes in

the overall dynamic characteristics of the machining system,

could result in crossing the stability limit, creating severe

chatter. For example, in a milling application, the amplitude

of chatter vibration can be limited by a provisional feed per

tooth reduction , until an established and desired speed has

been achieved oering a stable D

35 ‘Circular interpolation’ ,

is a block of entered information di-

recting the CNC system to cut, either an arc, or a circle, (e.g.

G02 – in a clockwise, or G03 anti-clockwise direction).

36 ‘Rigidity square rule’ – for milling cutters states: ‘Cutter rigid-

ity decreases by the ‘square’* of the distance from the holder’

(Smith, 1993, et al.).

For example, if a cutter ‘stood-out’ from its respective tool-

holder by 50 mm to mill a circular feature (Fig.158 – le), then,

if all other machining conditions remained the same and, then

cutter was replaced by one of 100 mm long (Fig. 158 – right),

it would now be 4 times less rigid, causing serious tool deec-

tion.

stand-o distances, conducive with correct and cur-

rent operational practices.

ere are several distinct problems involved in the

milling high-quality circular interpolated features and,

a slight digression into basic machine tool induced-er-

rors is necessary to clarify the circumstances for the

problems exhibited in Fig. 159. Most of today’s ma-

chine tools have what is termed ‘orthogonally-orien-

tated axes’

and in the case of the popular three-axis

vertical machining centre congurations, if the axes

have not been recently calibrated, then considerable

‘error’

can be introduced into the nal milled part

features. It has been well-proven that a machine tool

equipped with three orthogonal sideways: ‘X-axis’;

‘Y-axis’ – in the horizontal plane, together with the

‘Z-axis’ – in the vertical plane, can introduce up to 21

kinematic ‘errors’ into the cutting process. e kine-

matics for any machine tool are quite complex, when it

has the ability to provide motion to all its axes simulta-

neously, although these errors are oen small, they are

37 ‘Orthogonally-orientated axes’ , (is briey mentioned in Foot-

note 2) refers to the fact that each axis is positioned at 90° with

respect to each other, oen situated on top of another axis.

For example, on a typical 3-axis vertical machining centre,

the ‘Y-axis’ sits on top of the ‘X-axis’ , but at right-angles to it,

conversely, the ‘Z-axis’ is situated at 90° to these axes – hence

the term ‘orthogonal’.

NB Non-orthogonal machine tools exist, oen having com-

plex ‘kinematics’* between ve and six axes. erefore with

these machine tools, in order to machine (i.e. mill) a straight-

line. all the axes must be in synchronised control to achieve

this linear action.

*Kinematics, comes from the Greek word ‘Kinesis’ , which

means ‘Motion’. It can be dened as: ‘e study of motion with-

out regard for the cause‘ (Lombardi, 2001). In machine tool

terminology, it refers to the translational eects of both lin-

ear and angular motions. It is principally concerned with the

eects of the ‘degrees of freedom’ for a ‘free-body’ in three-di-

mensional space (also see: Footnote 47, in Chapter 3).

38 ‘Error’ is now not considered as an appropriate metrological

term for any form of calibration, the recommended term to-

day, is: ‘uncertainty’*.

*‘Uncertainty’ , has been simply dened as: ‘e doubt that

exists about the result of any measurement’ (Bell/NPL, 1999).

is is why today, uncertainty in measurement is a combina-

tion of many factors, some physical, while others are induced.

Hence, another term, along with all of these uncertainty fac-

tors has been coined, which is its ‘Uncertainty budget’ – this

being a simple mathematical calculation, based upon a sum-

mary of these uncertainty calculations.

Machinability and Surface Integrity 301