Smith G.T. Cutting Tool Technology: Industrial Handbook
Подождите немного. Документ загружается.

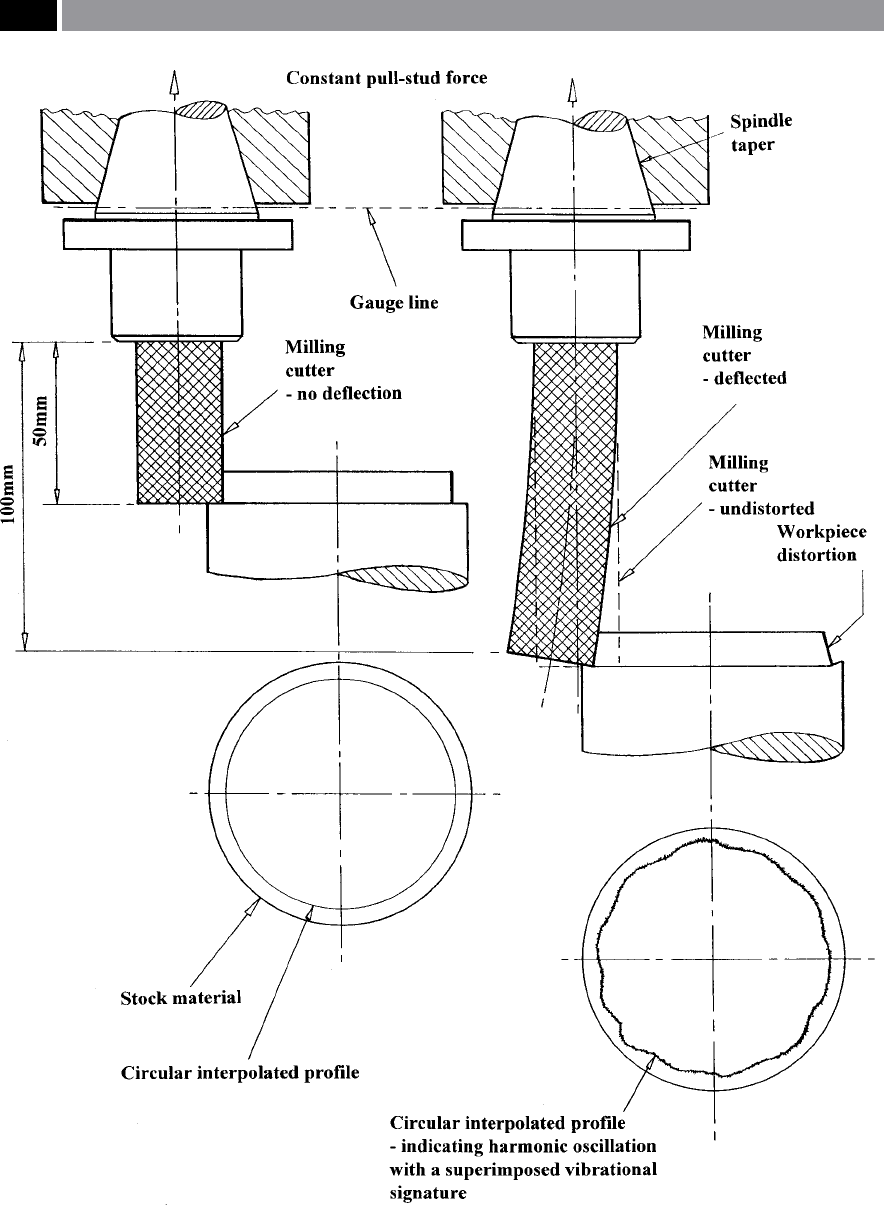
Figure 158. The eect of increased milling cutter length on the resultant circular interpolated prole on the workpiece.
302 Chapter 7
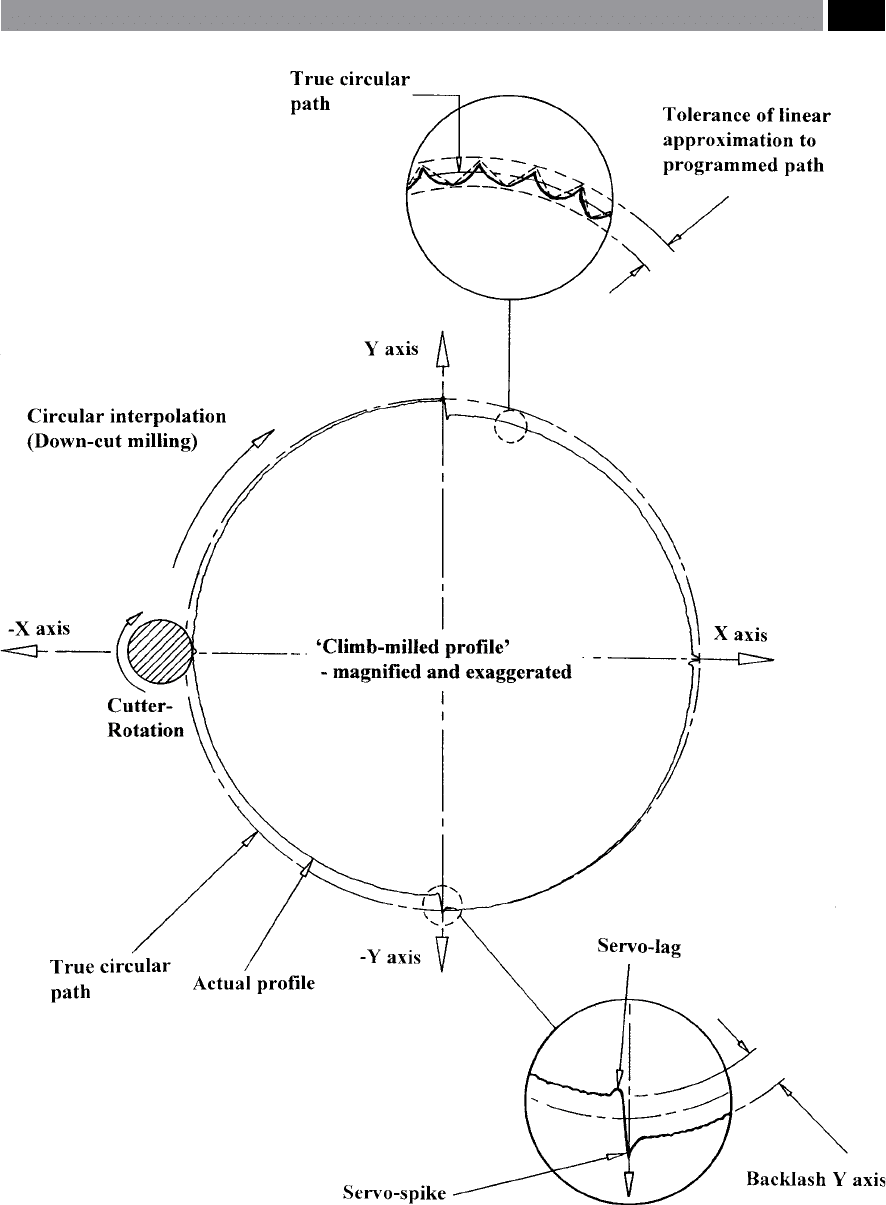
Figure 159. The generated errors produced when circular interpolating at high feedrates when high-speed machining.
Machinability and Surface Integrity 303

but signicant ‘errors’ , which can be said to be simplis-
tically produced as a result of:
•
Linear motions (six) – created by the displacement
of the forward-and-backward motion of the X-, Y-
and Z-axes slideway movements, introducing par-
ticular non-linearities into the slideway position-
ing,
•
Rotational motions (three) – yaw, pitch and roll for
each axis. All of these partial rotational motions can
be practically-described in the following manner:
•
Yaw is the side-to-side ‘crabbing-motion’ along the
slideway,
NB ‘Yaw’ is normally the result of too much clear-
ance (i.e. ‘slop’) in the adjacent slideway members.
•
Pitch introduces a backward-and-forward rock-
ing (pitching) action normal to the slideway, as the
moving element traverses along the axis,
NB ‘Pitching’ is probably due to the ‘prole/wavi-
ness’ (i.e. long-frequency eects) in its respective
slideway.
•
Roll is the clockwise-and-anticlockwise rotational
motion along the slideway.
NB ’Roll’ could be introduced by two ‘adjacent
ways’ situated on each slideway, but not being coin-
cident with respect to each other (i.e. laying in the
same respective plane), causing a limited pivoting
action – along the ‘line-of-sight’ of the axis as it tra-
verses along its length.
•
Squareness (three) – these ‘errors’ occur due to the
fact that each axis may not be at 90° (i.e. square) to
one another.
ese types of 21 ‘kinematic machine-induced er-
rors’ can be appreciably reduced by the application of
calibration through laser-based techniques. To a lesser
extent, these ‘errors’ can be minimised via ballbar ar-
tifact-based methods, oering a quick ‘health-check’
by either static, or dynamic assessment techniques.
e results of either the laser, or ballbar, can be fed
back into the machine’s CNC controller for dynamic
corrections as cutting takes place, oering a consid-
erable improvement in the machine’s subsequent ac-
curacy and precision. e above machine tool calibra-
tion techniques are somewhat beyond the scope of the
present discussion, the same could be said for ‘ther-
mally-induced e
rrors’ , however, they can also inuence
the machined part surface and the machine tool’s pro-
ling abilities. Moreover, ‘error-mapping techniques’
and sophisticated in-process control by an associated
‘dynamic error compensation system’ ,
have been shown
to extensively reduce the eects of the ‘variety of er-
rors’ that can be present on the machine tool, but once
again, these topics are mentioned only for further re-
search applications – as necessary.
e circular interpolated milled prole shown in
Fig. 159, shows signicant departures from roundness
of the milled workpiece, which is a function of most of
the previously discussed kinematically- and thermally-
i
nduced machine tool ‘errors’ , together with the possi-
bility of some ‘load-induced errors’. is diagrammatic
representation (i.e. Fig. 159), indicates that several
‘errors’ on the milled circular interpolated prole are
present. At relatively slow simultaneous feeding-mo-
tions of the two axes (‘X-’ and ‘Y-axis’), it will generate
a reasonable facsimile of the required circular feature.
However, then by somewhat increasing this milled in-
terpolation speed, the apparent roundness will appre-
ciably degrade, the reasons for this degradation, might
be the result of:
•
Servo-spikes – these unwanted eects occur at the
‘axis transition points’
39
at their respective 90° angu-
lar intervals, oen termed ‘quadrant-points’ ,
•
Back-lash – possibly resulting from any form of
axis reversals, originating from the recirculating
ballscrews
40
, creating a slight ‘o-set’ , or ‘mismatch’
at the axis transition points,
•
Servo-errors – when both axes are simultaneously
moving, their respective linear speed should be
39 ‘Axis transition points’ , are where the ‘servo-spikes’ occur.
ey result from a reversal of one of the axes at this angular
position and, its associated motor power-surge creating this
‘spike’. Normally, the ‘spike’ is associated aerward by a cor-
responding, but very small localised slack here, as axis take-up
begins once more at these ‘quadrant-points’ on the circular-
interpolated feature (i.e. see the inset and magnied diagram
in Fig. 159).
40
‘Recirculating ballscrews’ ,
are not supposed to have any ap-
preciable back-lash present, as they are normally pre-stressed
by applying loads by the application of either: tension-, or
compression-shimming. However, as the pitch of any the screw
has minute errors present, these are usually ‘mapped-out’ by
the original machine tool builder – using the recognised In-
ternational Standard laser-calibration techniques. Although,
once the machine tool has been operating for sometime and
either local ballscrew-wear occurs, or perhaps the machine
has had the occasional ‘tool-crash’ , this can introduce and af-
fect both its pitching- and back-lash-errors.
304 Chapter 7

perfectly matched, allowing either a partial arc,
or circular feature to be reproduced. If non-syn-
chronised motion occurs, oen termed ‘servo-mis-
m
atch’
41
between these two axes, then an elliptical
prole – usually inclined at an 45° angle occurs,
•
Squareness – when orthogonal (squareness) is not
maintained between the two interpolating axes,
then the net result will look similar to that of a
milled angular elliptical prole shape, which is un-
aected by the selected circular interpolation rota-
tional direction.
Considerably more machine tool-induced factors can
aect a milled circular interpolated prole. ese ‘er-
rors’ can be found, isolated and then reduced by di-
agnostically interrogation by using dynamic artefacts,
such as the ballbar. Ballbars and their associated in-
strumentation can not only nd the sources of error,
they can prioritise their respective magnitudes – to
show where the main ‘error-sources’ occur, then in-
stigate any feed corrections into the CNC controller
to nullify these ‘machine-induced errors’. As a result
o
f eliminating such ‘error-sources’ , this enables the
milled circular contouring and overall performance to
be appreciably enhanced.
7.5 Machined Surface Texture
Introduction to Surface Tex ture Parameters
When a designer develops the features for a component
with the requirement to be subsequently machined
utilising a computer-aided design (CAD) system, or
by using a draughting head and its associated draw-
ing board, the designer’s neat lines delineate the de-
sired surface condition, which can be further specied
by the requirement for specic geometric tolerances.
In reality, this designed workpiece surface condition
cannot actually exist, as it results from process-in-
duced surface texture modications. Regardless of the
method of manufacture, an engineering surface must
have some form of ‘topography, or texture’ associated
41 ‘Servo-mismatch’ , can oen be mistaken for a ‘squareness er-
ror’ , but if the contouring interpolation direction is changed,
from G02 (clockwise) to G03 (anti-clockwise) rotation, then
an elliptical prole will ‘mirror-image’ (‘ip‘) to that of the op-
posite prole – which does not occur in ‘squareness errors’.
with it, resulting from a combination of several inter-
related factors, such as the:
•
Inuence of the workpiece material’s microstruc-
ture,
•
Surface generation method which includes the cut-
ting insert’s action, associated actual cutting data
and the eect of cutting uid – if any,
•
Instability may be present during the production
machining process, causing induced chatter, result-
ing from poor loop-stiness between the machine-
tooling-workpiece system and chosen cutting data,
•
Inherent residual stresses within the workpiece
can occur, promoted by internal ‘
stress patterns’
42
–
causing latent deformations in the machined com-
ponent.
From the restrictions resulting from a component’s
manufacture, a designer must select a functional sur-
face condition that will suit the operational constraints
f
or either a ‘rough’ , or ‘smooth’ workpiece surface. is
then raises the question, posed well-over 25 years ago –
which is still a problem today, namely: ‘How smooth is
smooth?’ is question is not as supercial as it might
at rst seem, because unless we can quantify a surface
accurately, we can only hope that it will function cor-
rectly in-service. In fact, a machined surface texture
condition is a complex state, resulting from a combi-
nation of three distinct superimposed topographical
conditions (i.e. as diagrammatically illustrated Fig.
160a), these being:
42 ‘Stress patterns’ , are to be expected in a machined compo-
nent, where: corners, undercuts, large changes in cross-sec-
tions from one adjacent workpiece feature to another, etc.,
produce localised zones of high stress, having the potential
outcome for subsequent component distortion. ‘Modelling’
a component’s geometry using techniques such as: nite ele-
ment analysis (FEA), or employing photo-elastic stress analy-
sis* models or similar simulation techniques, will highlight
these potential regions of stress build-up, allowing a designer
to nullify, or at worst, minimise these potential undesirable
stress regions in the component’s design.
*Photo-elastic stress analysis displays a stress-eld, normally
a duplicate of the part geometry made from a thin two-dimen-
sional (planar) nematic liquid crystal, or more robustly from
a three-dimensional Perspex model, which is then observed
through polarised light source. is polarised condition, will
highlight any high-intensity stress-eld concentrations in the
part , which allows the ‘polarised model’ to be manipulated
by applying either an un-axial tension, or perhaps a bi-axial
bending external stress to this model, showing dynamically its
potential stress behaviour during its intended in-service con-
dition.
Machinability and Surface Integrity 305
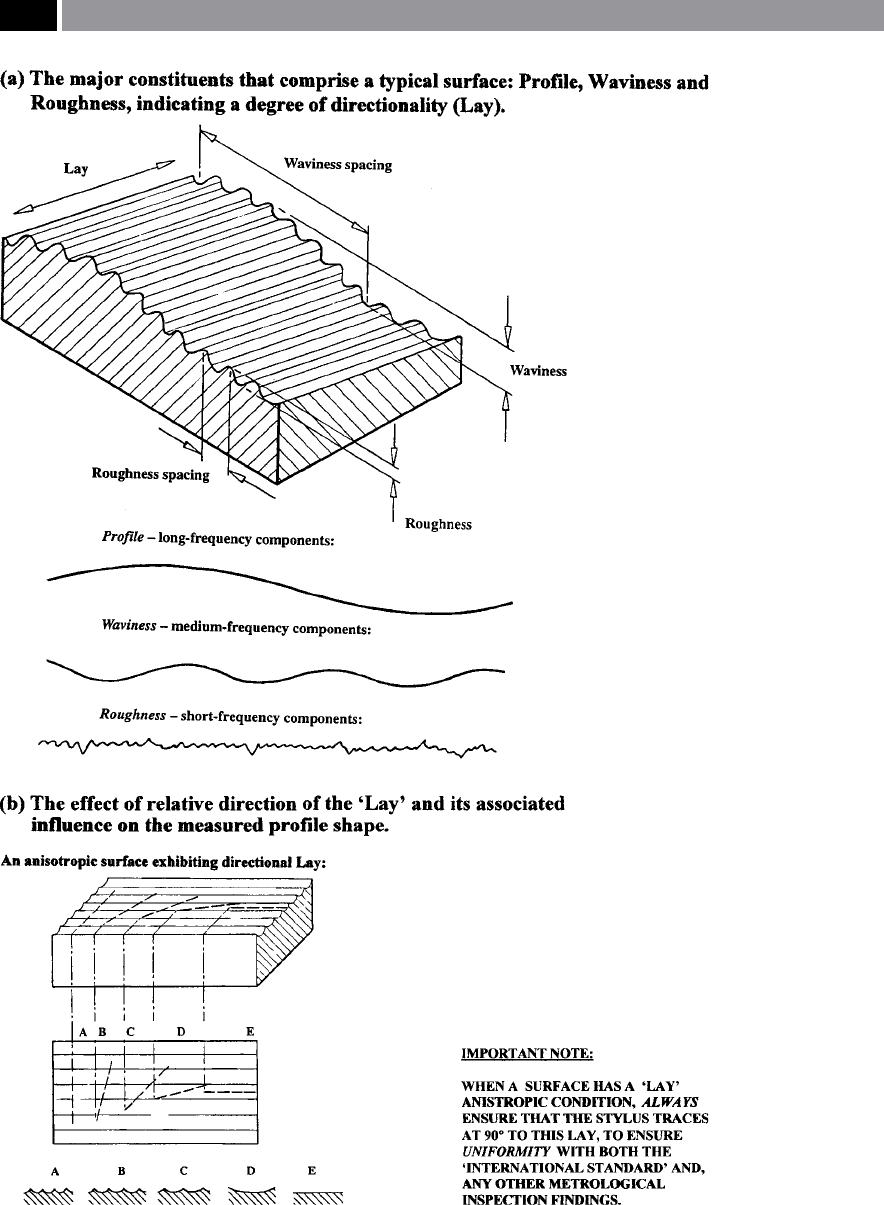
Figure 160. Surface texture comprises of: ‘long-’, ‘medium-’ and ‘short-components’, together with the
‘direction of the dominant pattern’ – superimposed upon each other. [Courtesy of Taylor Hobson]
.
306 Chapter 7
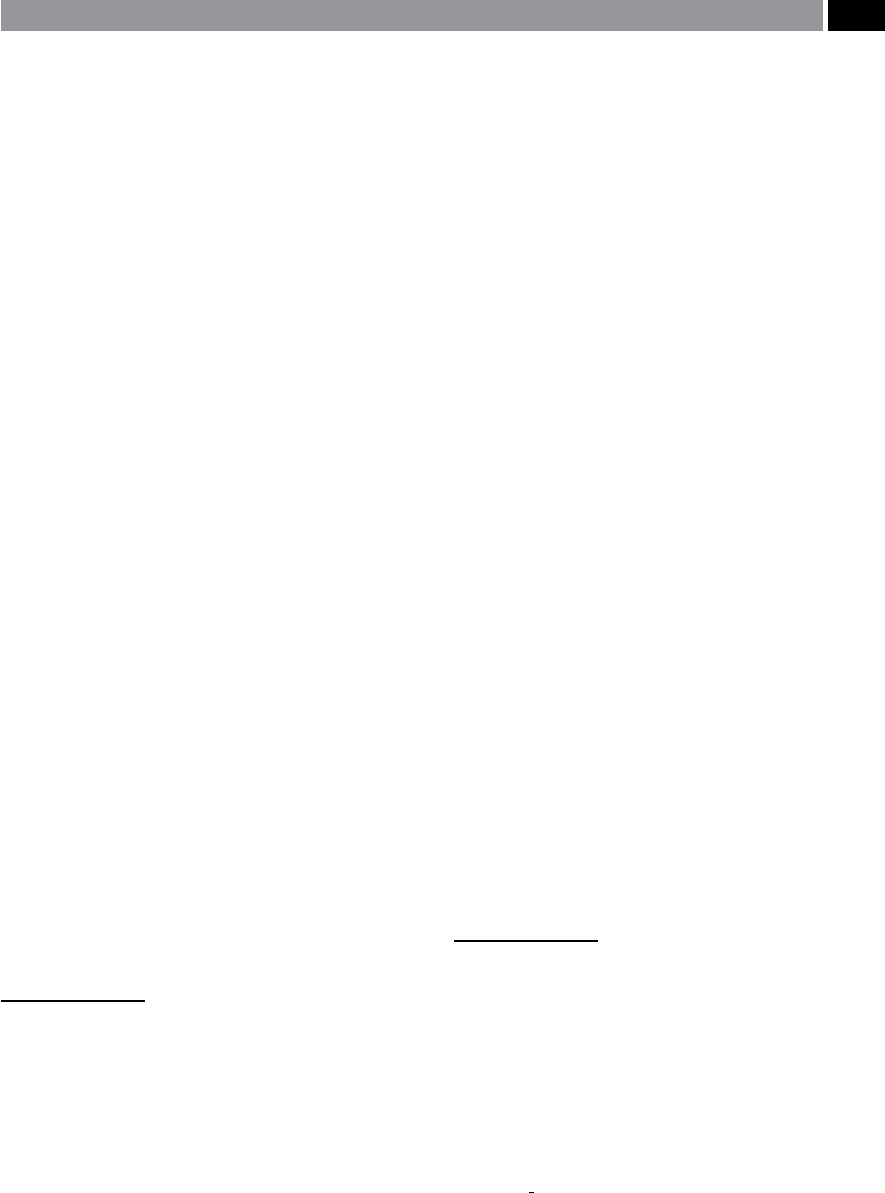
1. Roughness – comprising of surface irregularities
occurring due to the mechanism of the machining
production process and its associated cutting insert
geometry,
2. Waviness – that surface texture element upon
which roughness is superimposed, created by fac-
tors such as the: machine tool, or workpiece deec-
tions, vibrations and chatter, material strain and
other extraneous eects,
3. Prole – represents the overall shape of the ma-
chined surface – ignoring any roughness and wavi-
ness variations present, being the result of perhaps
the long-frequency machine tool slideway errors.
e above surface topography distinctions tend to be
qualitative – not expressible as a number – yet have
considerable practical importance, being an estab-
lished procedure that is functionally sound. e com-
bination of roughness and waviness surface texture
components, plus the surface’s associated ‘Lay’
43
are
shown in Fig. 160a. e ‘Prole’ is not depicted, as it
is a long-frequency component and at best, only its
partial aect would be present here, on this diagram.
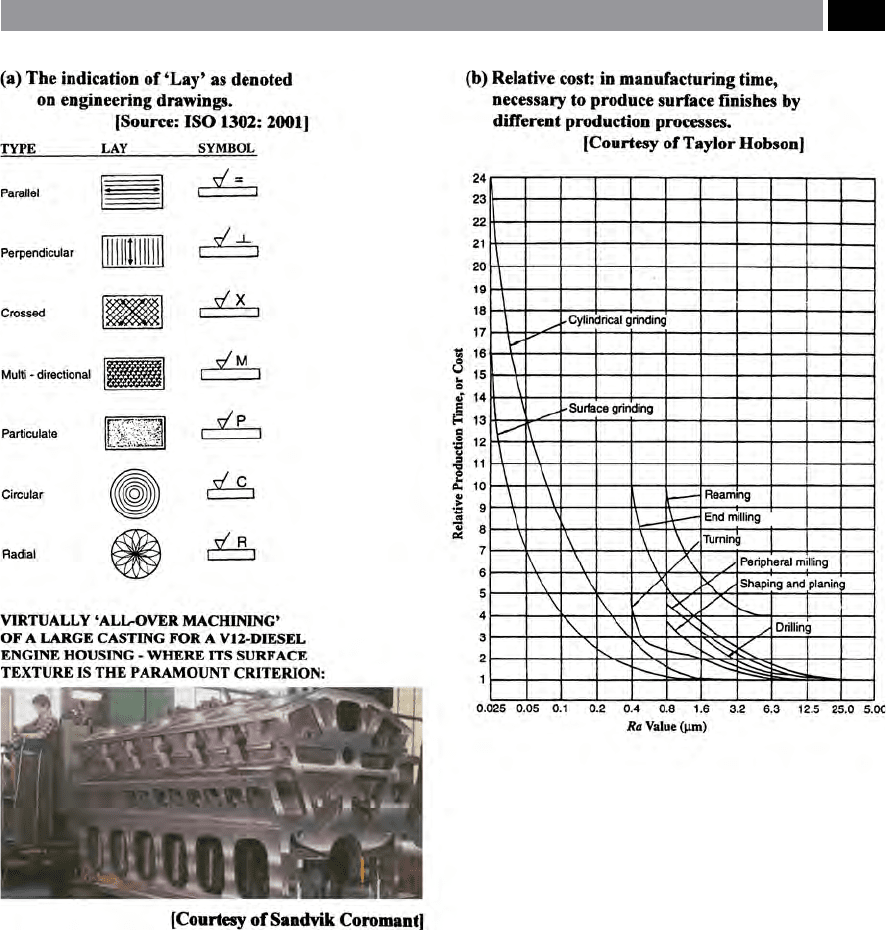
e ‘Lay’ of a surface tends to be either: anisotropic,
or isotropic
44
in nature on a machined surface topog-
raphy. When attempting to characterise the potential
functional performance of a surface, if an anisotropic
‘lay-condition’ occurs, then its presence becomes of
vital importance. If the surface texture instrument’s
stylus direction of the trace’s motion over the assessed
topography is not taken into account, then totally mis-
representative readings result for an anisotropic sur-
face condition occur – as depicted in Fig. 160b. is
is not the case for an isotropic surface topography, as
relatively uniform set of results will be present, regard-
less of the stylus trace direction across the surface (i.e.
43 ‘Lay’ , can simply be dened as: e direction of the dominant
pattern’ (Dagnall, 1998).
44 ‘Anisotropic, or isotropic surfaces, either condition can be in-
dividually represented on all machined surfaces. Anisotropy,
refers to a surface topography having directional properties,
that is a dened ‘Lay’ , being represented by machined feed-
marks (e.g. turned, shaped, planed surfaces, etc.). Conversely,
an isotropic surface is devoid of a predominant ‘Lay’ direc-
tion, invariably having identical surface topography charac-
teristics in all directions (e.g. shot-peening/-blasting and, to a
lesser extent a multi-directional surface-milling, or a radially-
ground surface, etc.).
see Fig. 161a – for an indication of the various clas-
sications for ‘Lay’).
Returning once more to Fig. 160b, as the stylus
trace obliquity changes from trace ‘A’ , inclining to-
ward trace ‘E’ , the surface topography when at ‘E’ has
now become at, giving a totally false impression of
the true nature of the actual surface condition. If this
machined workpiece was to be used in a critical and
highly-stressed in-service environment, then the user
would have a false sense of the component’s potential
fatigue
45
characteristics, potentially resulting in ei-
ther premature failure, or at worst, catastrophic fail-
ure conditions. In Fig. 162, the numerical data (ISO
1302:2001), has been developed to establish and de-
ne relative roughness grades for typical production
processes. However, some caution should be taken
when utilising these values for control of the surface
condition, because they can misrepresent the actual
state of the surface topography, being based solely on a
derived numerical value for height. What is more, the
‘N-number’ has been used to ascertain the arithmetic
roughness ‘Ra’ value – with more being mentioned on
this and other parameters shortly. e actual ‘N-value’
being just one number to cover a spread of potential
‘Ra’ values for that production process. Neverthe-
less, this single numerical value has its merit, in that
it ‘globally-denes’ a roughness value (i.e.‘Ra’) and
its accompanying ‘N-roughness grade’ , which can be
used by a designer to specify in particular a desired
surface condition, this being correlated to a specic
production process. e spread of the roughness for a
specic production process has been established from
experimental data over the years – covering the maxi-
mum expected ‘variance’
46
– which can be modied
45 ‘Fatigue’ , can be dened as: ‘e process of repeated load, or
strain application to a specimen, or component’ (Schaer, et
al., 1999). Hence, any engineering component subjected to
repeated loading over a prescribed time-base, will normally
undergo either partial, or complete fatigue.
46 ‘Variance’ , is a statistical term this being based upon the
standard deviation, which is normally denoted by the Greek
symbol ‘σ’. us, variance can be dened as: ‘e mean of the
squares of the standard deviation’ (Bajpai, et al., 1979).
us, σ = √Variance, or more specically for production op-
erations:
�
s =
�
�n − ċ
n
�
j=
(x
j
−
¯
x)
*s = the standard deviation of a sample from a production
batch run.
Machinability and Surface Integrity 307

depending upon whether a ne, medium, or coarse
surface texture is obligatory. Due to the variability in
any production process being one of a ‘stochastic out-
pu
t’
47
, such surface texture values do not reect the
likely in-service performance of the part. Neither the
surface topography, nor its associated integrity has
been quantied by assigning to a surface representa-
tive numerical parameters. In many instances, ‘surface
e
ngineering’
48
is utilised to enhance specic compo-
nent in-service condition.
It was mentioned above that in many in-service
engineering applications the accompanying surface
texture is closely allied to its functional performance,
predominantly when one, or more surfaces are in mo-
tion with respect to an adjacent surface. is close
proximity between two mating surfaces, suggests that
the smoother the surface the better, but this is not nec-
essarily true if the surfaces in question are required to
maintain an ecient lubrication lm between them.
e apparent roughness of one of these surfaces with
respect to the other, enables it to retain a ‘holding-
lm’ in its associated topographical ‘valleys’
49
. While
another critical factor that might limit the designer’s
choice of the smoothness of an engineering surface’s
selection, is related to its production cost (i.e. see
Fig. 161b). erefore, if the designer requires a very
smooth machined surface, it should be recognised that
its manufacturing time is considerably longer – so its
respective cost will be greater to that of a rough sur-
face, this being exacerbated by a very close dimen-
sional tolerance requirement.
47 ‘Stochastic processes’ , are dened as: ‘A process which has a
measurable output and operating under a stable set of condi-
tions which causes the output to vary about a central value in a
predictable manner’ (Stout, 1985).
48 ‘Surface engineering’ ,
is applying suitable discrete technolo-
gies to create surface lms (e.g. 10 to 100 nm thick), or by ma-
nipulating the surface atomic layers (e.g. 2 to 10 atomic layers,
approximately 0.5 to 3 nm), to enhance the ‘engineered’ sur-
face condition (i.e. Source: Vickerman, 2000).
49 ‘Surfaces’ ,
are recognised to have topographical features that
mimic the natural world. So a regular/irregular engineering
surface can exhibit both peaks and valleys, not unlike moun-
tainous terrain.
7.5.1 Parameters for Machined
Surface Evaluation
In order that a machined workpiece’s surface texture
can be determined using stylus-based (two-dimen-
sional) instrumentation, three characteristic lengths
are associated with this surface’s prole (i.e. see
Fig. 163a), these are:
1. Sampling length
50
– is determined from: the length
in the direction of the X-axis used for identifying
t
he irregularities that characterise the prole under
evaluation. erefore, virtually all surface de-
scriptors (i.e. parameters) necessitate evaluation
over the sampling length. Reliability of the data
is enhanced by taking an average of the sampling
lengths as depicted by the evaluation length shown
in Fig. 162a. Most of today’s stylus-based surface
texture instruments undertake this calculation au-
tomatically,
2. Sampling length – can be established as: the to-
tal length in the X-axis used for the assessment of
the prole under evaluation. From Fig. 163a, this
length may include several sampling lengths – typi-
cally ve – being the normal practice in evaluating
roughness and waviness proles. e evaluation
length measurement is the sum of the individual
sampling lengths (i.e. it is common practice to em-
p
loy a 0.8 mm sampling length for most surface
texture assessments),
3
. Traverse length – can be dened as: the total
length of the surface traversed by the stylus in mak-
ing a measurement. e traverse length will nor-
mally be longer than the evaluation length (i.e. see
Fig. 163a), this is due to the necessity of allowing
‘run-up’ and ‘over-travel’ at each end of the evalua-
tion length. ese additional distances ensure that
any mechanical and electrical transients, together
lter edge eects are excluded from the measure-
ment.
50 ‘Sampling length’ , is oen termed ‘Meter cut-o ’ , or simply
the ‘cut-o ’ length and its units are millimetres. e most
common cut-os are: 0.25, 0.8, 2.5, 8.0, 25.0 mm. e 0.8 mm
sampling length will cover most machining production pro-
cesses. In any surface texture evaluation, it is essential that the
cut-o is made known to the Inspector/Metrologist reviewing
this surface topographical data.
308 Chapter 7
e number of two-dimensional surface prole pa-
rameters that have been developed over the years for
just the stylus-based instruments – discounting the
three-dimensional contact and non-contact varieties,
has created a situation where many users simply do
not understand, nor indeed comprehend the intrinsic
dierences between them! A term was coined some
years ago to show exasperation by many metrolo-
gists’ with this ever-increasing development of such
parameters. Many researchers and companies were
totally disenchanted with their confunsion and plight,
so they simply called the predicament: ‘parameter-
rash’. However, here we need not concern ourselves
w
ith this ‘vast expanse of surface descriptors’ , as only
a few of the well-established parameters and discuss
just the most widely-utilised ones. It is worth making
Figure 161. ‘Lay’ indicated on drawings, plus the relative cost of manufacture for dierent production processes.
Machinability and Surface Integrity 309
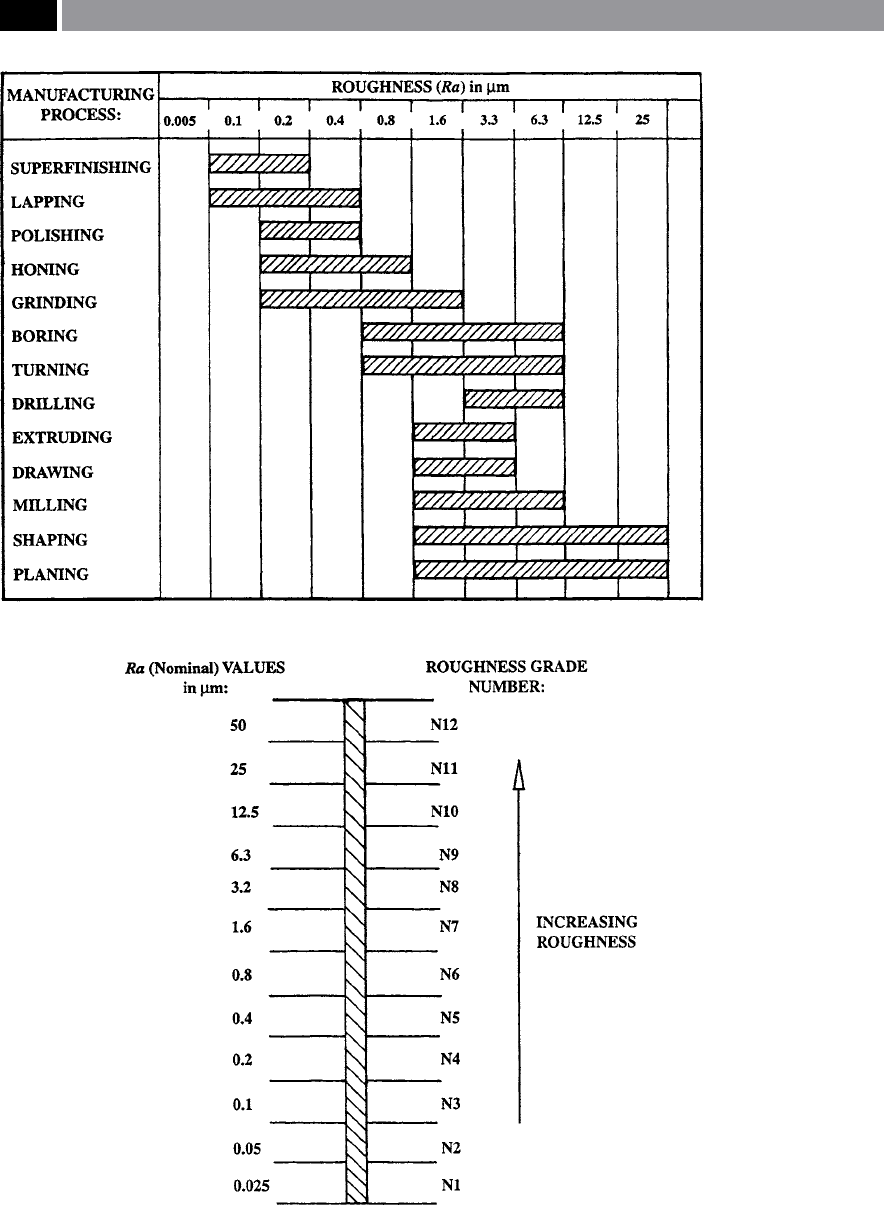
Figure 162. Anticipated process ‘roughness’ and their respective grades. [Source: ISO 1302, 2001].
310 Chapter 7
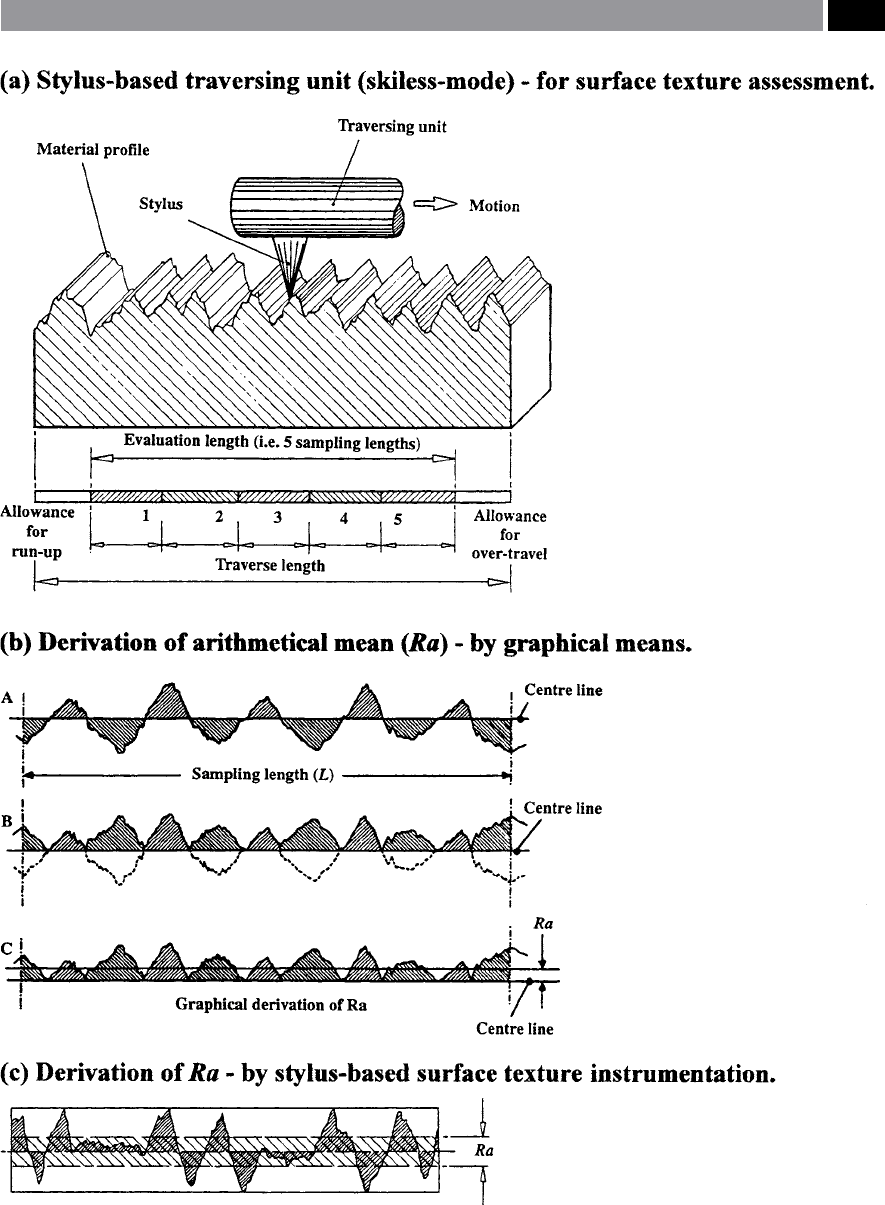
Figure 163. Surface texture data-capture, with techniques for the derivation of the arithmetic roughness parameter: Ra.
Machinability and Surface Integrity 311
