Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1

Подождите немного. Документ загружается.

§1.

Лінійні простори. Підпростори

131

Дайте означення матриці системи векторів х,,

,...,

у даному базисі.

8. Як визначити, чи є система т векторів п -вимірного

лінійного простору лінійно незалежною, якщо відомі коорди-

нати векторів у деякому базисі?

9. Дайте означення матриці переходу від одного базису до

другого.

10.

Чи може будь-яка матриця Т порядку п бути матрицею

переходу від одного базису до другого у п -вимірному просторі?

11.

Запишіть формули перетворення координат вектора х,

якщо відома матриця переходу від базису {е,-} до базису \е]}.

12.

Дайте означення підпростору лінійного простору X .

13.

Дайте означення лінійної оболонки системи векторів.

///. Приклади розв'язання задач

Приклад 1. З'ясувати, чи є дійсним лінійним простором

множина усіх дійсних матриць другого порядку.

• Оскільки при додаванні дійсних матриць другого порядку, а також

при множенні матриці на дійсне число одержуємо дійсні матриці другого

порядку, введені операції є операціями на даній множині. Аксіоми 1 - 8

лінійного простору виконуються. Дійсно, вказані у цих аксіомах операції

над матрицями другого порядку зводяться до відповідних операцій над

дійсними числами, для яких аксіоми

- 8, як відомо, мають місце. Отже, мно-

жина усіх дійсних матриць другого порядку є дійсним лінійним простором.

Приклад 2. З'ясувати, чи є лінійно незалежною система

векторів

(2 0^ Ґ1 2^

Го -Г]

0 0)

лінійного дійсного простору квадратних матриць другого

порядку.

132

Глава 4. Лінійні простори. Евклідів простір

• Наведена система векторів є лінійно незалежною, оскільки рівність

«і

(2 0]

Гі

Го

-г

'о о

[о о

+ а

[о о

ч°

о/

або

'2а!

+ а

2а

-а

'0 0'

)

справедлива тільки тоді, коли а. = а

= а

= 0

Дійсно, наведена рівність матриць має місце тільки тоді, коли

2аі + а

2а

- а

= 0;

=0,

а ця система має єдиний розв'язок - нульовий. А

Приклад 3. Довести, що у лінійному дійсному просторі

дійсних квадратних матриць другого порядку вектори

А =

утворюють базис, і знайти в цьому базисі координати вектора

( 2 6~\

-З 5

°1

Го

°1

Го

°1

>е

,0 о,

>Ь =

о,

>*4 =

-1

X =

або

• Вектори

в],

, £

, е

лінійно незалежні, тому що рівність

а,

а, 20.2} Г0 (Л

'\ 0^ '0

'0 0^ '0 0' '0 <Л

,о о,

+ а

,о о,

+ а

,3 о,

+ а

ч0

-1

ч0 о,

Да

;

0 0

виконується тільки при а] = а

= а

= 0.

§1.

Лінійні простори. Підпростори

133

Легко переконатися у тому, що будь-який вектор простору, який розг-

лядається, лінійно виражається через вектори , е

, е

. Отже, вектори

е\, е

, е

утворюють базис.

Позначимо координати вектора х у даному базисі через Р], р

, р

Тоді

= Рі

«1

+ Рг «2 +

Рз

з + Р4 «4,

або

2 6

-З 5

1 0

,0 о,

+Р;

0 2^

,0 0

+ Рз

'0 0^

о,

+р<

0 -1

( 2 6Ї

,-3 5

( Рі 2р

ЗРз -Р

звідки Рі=2, 2р

=6, Зр

=-3, -р

=5. Отже, Рі=2, Р

=3,

Рз =

-1,

= -5 - шукані координати.

Приклад

4. У лінійному дійсному просторі дійсних квад-

ратних

матриць другого порядку знайти матрицю переходу

від

базису

до

базису

Ґ1

Го

°]

Го

о'

о,

,і

о,

—

Гі

Го

°1

3 =

4 =

-1

т =

•

3 умови випливає, що е\=2еі,

=Є]+2<?

=2е

+3е

= -<?4 . Матриця

'2 1 0 0^1

0 2 2 0

0 0 3 0

0 0 0 -1,

в у -му (у = 1, 4) стовпці якої стоять координати вектора е'у у базисі

е\, е

, е

, є матрицею переходу від базису е\, е

, е

до бази-

су е[, е

, е

, е\ . <

134

Глава 4. Лінійні простори. Евклідів простір

Приклад 5. Задана матриця Т -

З -2

переходу

ВІД

базису е

, е

до базису е,, е

. Знайти координати вектора

а -4е

+е

у базисі е[, е'

• Відомо, що X' - Т

Х , де X та X' - матриці-стовпці з коор-

динат вектора а відповідно в базисах е

, е

та е[, е

. З того, що

-і 1

2 2

маємо

Х'

і з у

( 2 2Л

х =

-1 З

ґлЛ ^

VI/

Отже, координатами вектора а в базисі е[, е'

будуть

тобто а =

—, -

—

І. ^

Приклад 6. Знайти координати геометричного вектора

х = —і+2і+к в базисі р', який складається з векторів

е[ = і

і, е'

= )'

к , е'

-і+к.

• Випишемо координати векторів е{,е

,ет, у вихідному базисі

Р = (7,М):

(о)

, Е'

1 0

Звідси матриця переходу 7р_>в'

має

вигляд

1 0 1

1 1 0

0 1 1

§1.

Лінійні простори. Підпростори

135

Обертаючи матрицю 7р->р,' та використовуючи вираз

X' = (7р_»р')

X, знаходимо

Г = (Т^рГ

Х=-

1 1-1

-1 1 1

1-1 1

-1>

тобто х = 2^2 -е$.4

Приклад

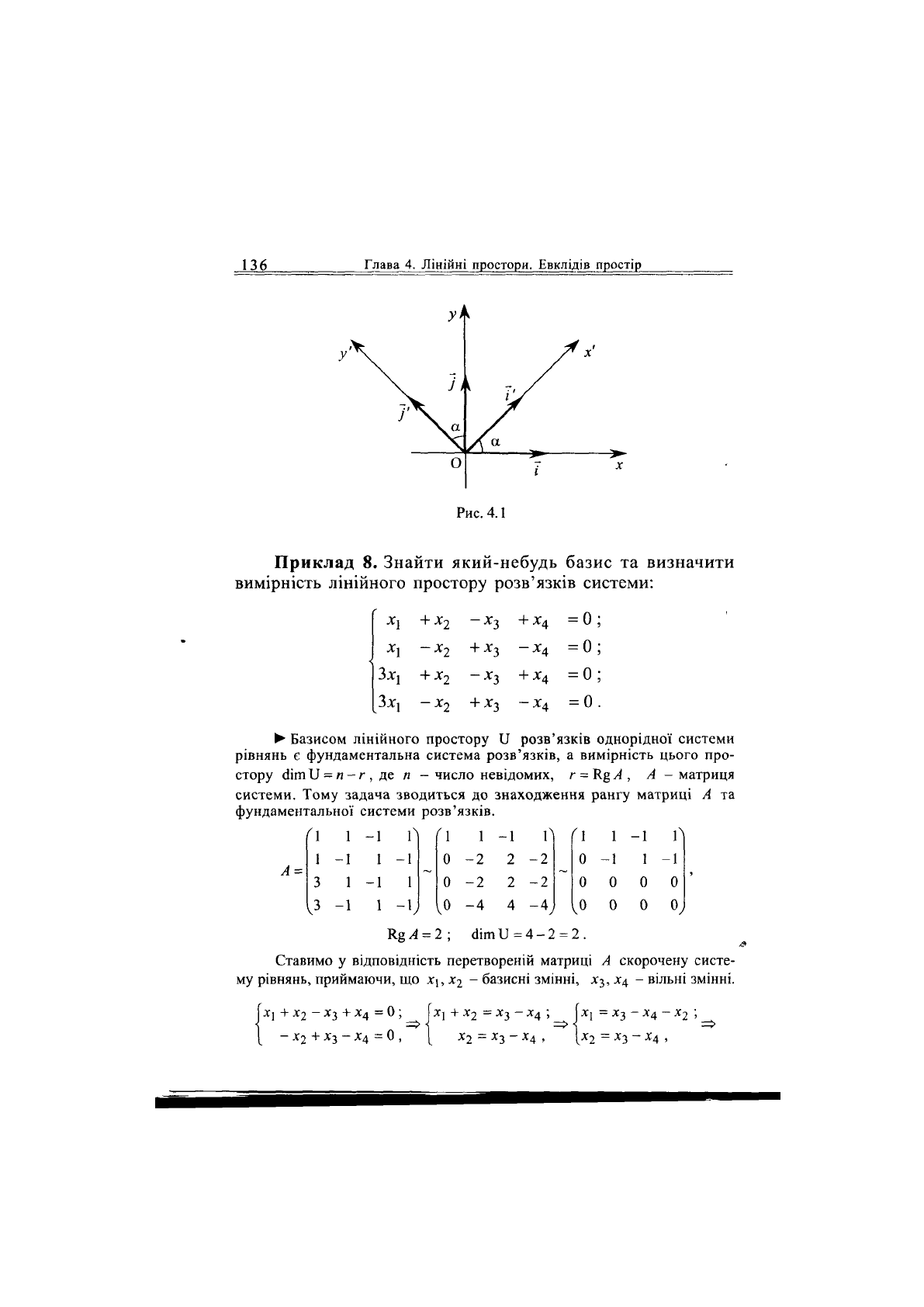
7. Система координат хОу повернута навко-

ло

початку координат на кут а (рис. 4.1). Виразити коорди-

нати

вектора а = хі

у] у новій системі координат через

його

координати у старій системі.

•

Розкладемо вектори /' та у" за ортами і та

і' = і соз а + у зіпа ,

у = / соз (—+ а) + у зт(—+ а) = -і зіпа + у соз а .

Запишемо матрицю переходу від старого базису /, у до нового /', у':

Т:

'соза -зіпа^

Враховуючи, що X = ТХ', маємо

х = х'со& а-.у'зіпа ,

у = х'зіпа +

у'соз

а.

Звідси отримуємо, що

х'

= хсов а+

3;зіпа

у'

= —х зіп а

у соз а

це координати вектора а у новій системі координат.

Отримали формули перетворення координат при повороті системи

координат при переході від нової системи координат до старої, і навпаки. -4

136

Глава 4. Лінійні простори, Евклідів простір

Приклад 8. Знайти який-небудь базис та визначити

вимірність лінійного простору розв'язків системи:

+ х

= 0;

-х

+ х

—

= 0;

+ х

= 0;

Зх,

-х

+ х

—

= 0.

• Базисом лінійного простору II розв'язків однорідної системи

рівнянь є фундаментальна система розв'язків, а вимірність цього про-

стору діт II = п-г , де п - число невідомих, г = К§

, А - матриця

системи. Тому задача зводиться до знаходження рангу матриці А та

фундаментальної системи розв'язків.

А =

-1

-2

-4

-1

-2

-4

КцА

= 2;

шти=4-2:

1 -1

-і

Ставимо у відповідність перетвореній матриці А скорочену систе-

му рівнянь, приймаючи, що х\,х

- базисні змінні, х

, х

- вільні змінні.

~ х

+ х

= 0 \

—

+ х

—

0 ,

X] + х

—

;

2 -

_ х

4 »

х,

—

= Ху

§1.

Лінійні

простори.

Підпростори

137

х\

= х

- х

+ х

= 0;

]

X] = 0;

= х

- х

, [х

= х

•

Х(с

)

= С\, с

єК.

Позначивши х

С],

отримуємо загальний розв'язок системи:

' 0 ^

Сі -с

Звідси отримуємо фундаментальну систему розв'язків:

' (Л

-1

'0^

=Х(1,0)

= , Е

=Х(0,ї)

Таким чином: аіт II = 2 .

Базис \] : Е\, Е

IV.

Задачі

для

практичних занять

У задачах 4.1 -4.5 перевірити, що дані множини є лінійни-

ми просторами.

4.1.

Множина У

усіх геометричних векторів (операції

над геометричними векторами визначені в §1, гл.1).

4.2.

Множина К" усіх арифметичних

-компонент-

них векторів х = (х

{

,... ,х

) (операції над арифметичними

векторами визначені в §1, гл.1).

4.3.

Множина

усіх многочленів

р(і)

і"~

... + а

( + а

степеня <

-1,

з природним чином введеними операціями

додавання многочленів та множення їх на числа.

4.4.

Множина усіх геометричних векторів, що виходять

з початку координат, кінці яких лежать на фіксованій прямій.

138

Глава 4. Лінійні простори. Евклідів простір

4.5. Множина усіх геометричних векторів, для яких вико-

нується умова

Зс

> а , де а > 0 - фіксоване число.

4.6. У просторі У

задані вектори

е\=і

]> е

=ї-], е\ = -і + 2у - к .

Довести, що система Р' = (Щ, е

, е

) - базис у У

, та записати

матрицю переходу , де Р= (е

= /, е

= у

;

, е

= к) . Знай-

ти координати вектора х = і - 2і + 2к в базисі Р'.

У задачах 4.7 - 4.8 знайти матрицю переходу 7р_>

-, де

Р= (і, у ,к) і Р'= (і', У, к') - ортонормовані базиси в У

, та за-

писати стовпець координат вектора х~і - 2)

к в базисі р'.

4.7. Базис р' отримано заміною на протилежний на-

прямок усіх трьох базисних ортів р.

4.8. Базис Р' отримано перестановкою і' = у, у =к,к - і.

4.9. З'ясувати, чи є лінійно незалежною система векторів

у просторі У

а) х, = Зі +7, х

=і - у;

б) х\ = 2/, х

= Зу;

ь)х

=і-2], х

=2у'-і;

г)х

=Г

у",

=2у, х

=4і-у.

4.10. З'ясувати, чи є лінійно незалежною система век-

торів у просторі У

а) х, =2і + 7, х

з£;

б) X] = і - 2у + Зк, х

= 4г + у , х

= 5і - у + Зк ;

в)х,=у'-3£,

=2г+4у, х

=5к.

§1.

Лінійні простори. Підпростори

139

4.11.

З'ясувати, чи є лінійно незалежною система векторів у

лінійному просторі квадратних матриць заданого порядку:

' 1 0

а)

в)

г)

Д)

1 1

' 2

ГО 2^

; б)

Г-і

(2 -ЛЛ

; б)

, о

0 -6,

о о

•1

1 о

'"1

'0 0^

0 1

-1

/ 1

1 0 о

0 1 о

0 0 0

Го 1

0 0 0"

о ,

1 0 0

)

і 1

4.12.

Знайти ранг та який-небудь базис системи геометрич-

них векторів Зс, = -і + 2і , х

2і -

у"

к , х

= -4г + 5} - к ,

= 3/

—

3у +

А:

4.13.

У просторі К

задані вектори е{ = (1,2,-1,-2),

е'

=(2,3,0,-1), е

=(1,2,1,4), е

= (1,3,-1,0). Довес-

ти,

що система

(3'

= (е{, е

, е

) - базис у К

, знайти мат-

рицю переходу 7р_>р-, де р - канонічний базис у К

. Знай-

ти координати вектора х = (7,14,-1,2) у базисі Р'.

< 4.14. Довести, що система многочленів 1,І,

,...

ут-

ворює базис у просторі Р„ усіх многочленів степеня < п - 1

і, отже, 6хтР

= п (цей базис називається канонічним). Знайти

координати:

а) многочлена р(() = -3/ +1 у канонічному базисі прос-

тору Р

;

б) многочлена ц (І) = і - 2 / у канонічному базисі прос-

тору Р

140

Глава 4. Лінійні простори. Евклідів простір

4.15. Довести, що система многочленів і

Х,

і +1

1 +

1, 1 лінійно незалежна.

4.16. Довести, що система многочленів і

+1,

-1

2(,

І - і утворює базис у просторі Р

. Виписати у цьому ба-

зисі стовпець координат многочлена р{і) = -2( +і-\.

4.17. Знайти координати многочлена р(і) = ( -1

2 у

базисі 1, 1-Х,

(/-і)

4.18. З'ясувати, чи утворює базис в арифметичному прос-

торі К

= {х = (а

, а

) | а, є К

}

задана система векторів:

а) (1,0, 0), (0,1,0), (0,0,1);

б) (1,2,-7), (0,3,1), (0,0,1);

в) (1,0, 0), (0,1,0), (1, 1,0);

г)(3,0,

5), (1,2,-1);

д) (1,2,-1), (2,3,4), (3,4,6), (-1,7,2).

4.19. З'ясувати, чи утворює базис у лінійному просторі

квадратних матриць А = (а

), а^єк, другого порядку дана

система векторів:

'0 0^

і о.

а)

б)

в)

г)

Д)

(х (А

.о о,

'І о']

\р °,

'1 0^

о о

Го П

,0 о

Го і

о о

0 4

«У

'о О

о 0

'о -П

о о

-1 7^

'0 0^

го 0^

1 о

о о

0 1

2 4

3 4^

0 7

(X 0^

1 0

'0 0^

0 -1

Г-і <Г\

0 5

'0 0^

5 7