Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§3.
Системи лінійних алгебраїчних рівнянь 121
Поклавши, наприклад, х
4
= 0, отримаємо частинний розв'язок
*(<>)
=
6
]_
6
1
Безпосередньою підстановкою в систему частинного розв'язку, впевнює-
мося у його правильності. -4
Приклад 7. Використовуючи метод повного виключення,
знайти матрицю, обернену матриці А :
А =
(2 З 4
Л
1 2 5
ч
4 7 6
( 2
3 4 1
0 0^
ґ
2 3 4 1 0 о
ч
(2 0 -14
4
-6 0^
• 1 2
5 0 1 0
~
о Ш 6 -1 2
0
~
0 1 6
-1 2
0
7 6 0 0 0 2
V
-4 -4 0
2
,
0
-16
-2 -4 2
'-32
0 0
-92
40
28"
\
0 0 92/32 -40/32
-28/32'
0
-16 0 28 -8 -12
~
0
1
0 -28/16 8/16 12/16
,
0
0 -16
- 2
-4
2
,
,°
0 1 2/16 4/16
- 2/16
у
Праворуч від вертикальної риски отримали обернену матрицю.
Отже,
А'
1
=
23/8 -10/8 -II
14/8
1/8
4/8
2/8
6/8
-1/8
1
Г-23 10 7^1
14 -4 -6
•1-2 1
Можна перевірити, що А А
А~
Х
А
= Е.<

122
Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
IV. Задачі для практичних занять
У задачах 3.109 - 3.116 розв 'язати системи за правилом Кра-
мера:
3.109.
3.111.
Зх -5у = 13 ;
3.113.
3<зх - 6Ьу = аЬ .
2х
+
у =5;
х + Зг = 16 ;
5^-2 = 10.
3.110.
3.112.
3.114.
[Зх-Ау =-6 ;
[Зх + 4;/ = 18.
7х+ 2.у+ 32 = 15 ;
5х- Зу
+
2г - 15 ;
10х-11>>+
52
= 36.
х + у - 2г - 6 ;
2х +
3у-72
= 16;
5х + 2^+ 2 = 16.
3.115.
3.116.
Ах
х
+ 4х
2
+ 5х
3
+ 5х
4
= 0 ;
2Х]
+ Зх
3
- х
4
= 10 ;
х
\ +
х
2 ~ - '•>
Зх
2
+ 2х
3
= 1.
2х] - х
2
+ Зх
3
+ 2х
4
= 4
3x2 + Зх
2
+ Зх
3
+ 2х
4
= 6
Зх|
—
х
2
х
3
2х
4
—
6
Зх] - х
2
+ Зх
3
—
х
4
=
6 .
У задачах 3.117-3.122 розв'язати системи матричним ме-
тодом:
3.117.
5х±
+ 8х
2
+ х
3
= 2 ;
Зх] - 2х
2
+ 6х
3
= -7 ;
2х} + х
2
—
х
3
=
—5
.

§3.
Системи лінійних алгебраїчних рівнянь
123
3.118.
2х,
—
Зх
2
+ х
3
—
—
7 ;
х
і
+ 4х
2 + -
-
1 '•>
X] - 4х
2
= -5 .
3.119.
3.120.
2х, + 2х
2
- х
3
+ х
4
= 4 ;
4х, + Зх
2
- х
3
+ 2х
4
= 6 ;
8х, + 5х
2
- Зх
3
+ 4х
4
= 12 ;
ЗХ] + Зх
2
- 2х
3
+ 2х
4
= 6 .
2х, + Зх
2
+11х
3
+ 5х
4
= 2 ;
х^ + х
2
-ь 5х
3
4- 2х
4
—
1;
2х] + х
2
+ Зх
3
+ 2х
4
= -3 ;
X) + х
2
+ Зх
3
+ 4х
4
= -3 .
У задачах 3.121-3.128 дослідити сумісність та знайти загаль-
ний розв'язок наступних систем. Використати метод Гаусса.
3.121.
2х- у
+
г = -2;
х
+
2у
+
32 =
-1;
х-3у-2г
= 3.
3.122.
х+2у-4г = 1;
2х+ у-5г = -\;
х-
у- 2=-2.
3.123.
3.124.
Зх|
—
2х
2
—
5х
3
-Ь х
4
—
З
2х, - Зх
2
+ х
3
+ 5х
4
=
—З
X} + 2х
2
- 4х
4
= -З
Х\ - х
2
- 4х
3
+ 9х
4
=22
х
\
+ х
2~ 6х
3
- 4х
4
=
Зх,
х
2
- 6х
3
- 4х
4
2х! + Зх
2
+ 9х
3
+ 2х
4
Зх, + 2х
2
+ Зх
3
+ 8х
4
:
6;
2;
6;
-7.

1 24 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
3.125.
3.126.
3.127.
2х
Зх
9х
Зх
їх
5х
9х
6х
Зх
3.128.
+ 1х
2
+
Зх
3
+ х
л
- 6 ;
+ 5х
2
+ 2х
3
+ 2х
4
= 4 ;
+ 4х
2
+ х
3
+ 7х
4
= 2 .
- 5х
2
+ 2х
3
+ 4х
4
= 2 ;
- 4х
2
+ х
3
+ Зх
4
= 5 ;
+ 7х
2
- 4х
3
- 6х
4
= 3 .
- Зх
2
+ 5х
3
+ 6х
4
= 4 ;
- 2х
2
+ Зх
3
+ 4х
4
= 5 ;
- х
2
+ Зх
3
+ 14х
4
= -8 .
х
і
+
х
2
+
_
2х
4
+ Зх
5
=
1
;
2х] + 2х
2
+ 4х
3
- х
4
+ Зх
5
= 2 ;
Зх] + Зх
2
+ 5х
3
- 2х
4
+ Зх
5
= 1;
2х) + 2х
2
+ 8х
3
- Зх
4
+ 9х
5
= 2 .
3.129. Підібрати параметр X, такий, щоб система
Зд^|
2.x 2
~т~
д^з
—
2
мала єдиний розв'язок.
3.130. За якого значення параметра X, система
2х,
х
2
+ х
3
Х|
Ч"
2х
2
"Ь
Зх
3
Я;
=
2:
Зх, - х
2
+ 2х
3
= З
має єдиний розв'язок?
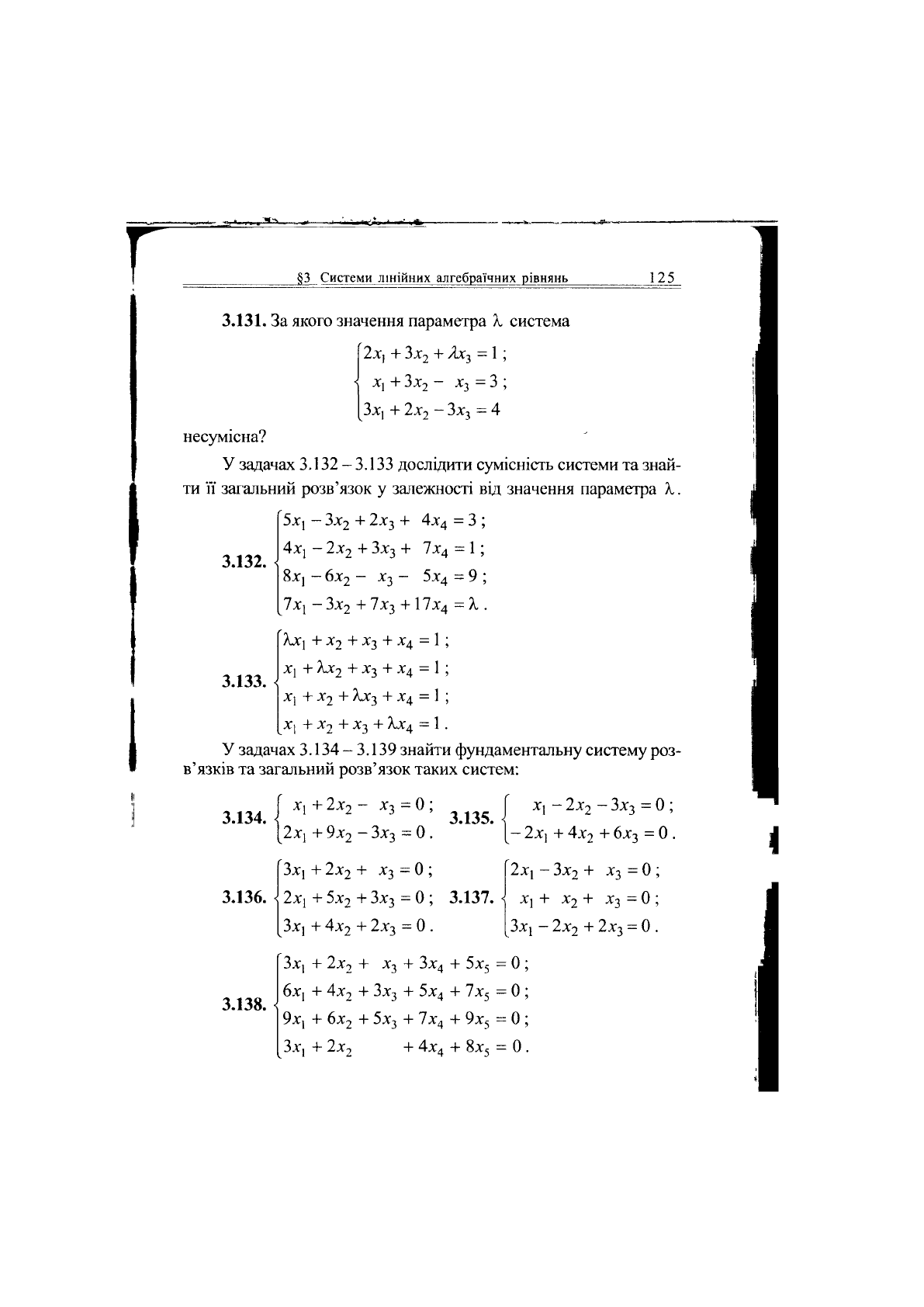
§3 Системи лінійних алгебраїчних рівнянь
125
3.131.
За якого значення параметра X система
3.132.
Зх, + 2х
2
- Зх
3
= 4
несумісна?
У задачах 3.132 -
3.133
дослідити сумісність системи та знай-
ти її загальний розв'язок у залежності від значення параметра X.
5х, - Зх
2
+ 2х
3
+ 4х
4
= 3 ;
4х, - 2х
2
+ Зх
3
+ 7х
4
= 1;
8х, 6х
2
х
3
5х
4
—
9 \
7х, - Зх
2
+ 7х
3
+ 17х
4
= X .
Хх\ + х
2
+ х
3
+ х
4
= 1
X, + Хх
2
+ Х
3
+ Х
4
= 1
X} + х
2
+ Хх
3
+ х
4
= 1
х, + х
2
+ х
3
+ А.х
4
= 1.
У задачах 3.134 - 3.139 знайти фундаментальну систему роз-
в'язків та загальний розв'язок таких систем:
3.133.
3.134.
3.136.
X! + 2х
2
- х
3
= 0 ;
3.135.
3.138.
2х, + 9х
2
- Зх
3
= 0 .
3X5 + 2*2
+ х
3
=
0 '
2х, + 5х
2
+ Зх
3
= 0
;
3.137
Зх, + 4х
2
+ 2х
3
= 0 .
Зх, + 2х
2
+ х
3
+ Зх
4
+ 5х
5
= 0
6х, + 4х
2
+ Зх
3
+ 5х
4
+ 7х
5
= 0
9х, + 6х
2
+ 5х
3
+ 7х
4
+ 9х
5
= 0
Зх, + 2х
2
+ 4х
4
+ 8х
5
= 0 .
х, - 2х
2
- Зх
3
= 0 ;
- 2х, + 4х
2
+ 6х
3
= 0 .
2х, - Зх
2
+ х
3
= 0 ;
X, + х
2
+ х
3
= 0;
Зх, - 2х
2
+ 2х
3
= 0 .

126 Глава 3. Визначники та матриці. Системи лінійних алгебраїчних рівнянь
2х, - 4х
2
+ 5х
3
+ Зх
4
= 0 ;
3.139.
<
Зх, - 6х
2
+ 4х
3
+ 2х
4
= 0 ;
4х] - 8х
2
+ 17х
3
+ 11х
4
= 0 .
У задачах 3.140-3.141 визначити значення параметра а, при
якому система має нетривіальні розв'язки, та знайти ці розв'язки.
а
х, + Зх
2
+ 2х
3
= 0 ;
3.140. \ а
х,-
х
2
+ х
3
= 0 ; 3.141.
8 х, + х, + 4х
я
= 0 .
2х, + х
2
+ Зх
3
= 0 ;
4х, х
2
+ 7х
3
0
х, + ах
2
+ 2х
3
= 0 .
У задачах 3.142-3.145 знайти загальний розв'язок неоднорід-
них систем, використовуючи фундаментальну систему розв'язків
відповідних однорідних систем.
3.142.
2х, -Ь х
2
х
3
х
4
4- х^
—
1
*
X,
—
х
2
4- х
3
4- х
4
—
2х^
—
0 і
Зх, + Зх
2
- Зх
3
- Зх
4
+ 4х
5
= 2 ;
4х, + 5х
2
- 5х
3
- 5х
4
+ 7х
5
= 3 .
3.143.
3.144.
3.145.
2.Х| 2д^2 ~і~ -^з
X]
+ 2х
2
х
4
+
х
5
= 1
4х,
2х,
10х
2
+ 5х
3
- 5х
4
+ 7х
5
=
14х
2
+7х
3
-7х
4
+11х
5
=-1.
х, х
2
4- х
3
х
4
4- х^
—
х^
—
1
*
2х,
—
2х
2
4- 2х
3
4- х
4
—
х^ 4- х^ = 1.
X]+2х
2
+3х
3
+4х
4
+5х
5
= 0;
х, 2х
2
—
Зх
3
4х
4
—
5х^ = 2
*
2х
2
4- Зх
3
+ 4х
4
+ 5х
5
= -1 .
У задачах 3.146 - 3.150 методом Жордана - Гаусса (повного
виключення) дослідити сумісність та знайти загальний розв'язок
таких систем:

§3.
Системи лінійних алгебраїчних рівнянь
127
3.146.
х
х
+ 2х
2
+ Зх
3
+ 4х
4
= О
7х, + 14х
2
+ 20х
3
+ 27х
4
= О
5х, + 10х
2
+ 16х
3
+ 19х
4
= -2
Зх, + 5х? + 6х, +
1
Зх
4
= 5
3.147.
Х|
~\~
Х*^
Х|
"4"
~г~
Х^
Х^
"4*
Х^
~\~
Х^
= і
= 4
= -3
Х^
Ч~
Х^
"4*
Х^ — 2
х
4
+ х
5
=
-1.
3.148.
105х! -175х
2
- 315х
3
+ 245х
4
= 84 ;
90х, - 150х
2
- 270х
3
+ 210х
4
= 72 ;
75х[ -125х
2
-225х
3
+ 175х
4
= 59 .
3.149.
8х, + 12х
2
14х, + 21х
2
9х
3
+ 11х
4
16х
3
+ 20х
4
= 20
= 35
= О
= 0.
10х
5
+ 12х
6
=22
15х
5
+ 18х
6
= 33
3.150.
7Х| ^-^*2 ^*^3 ^"-^4 — ^
•
Зх, + 2х
2
+ х
3
+ 2х
4
= -З
2х
;
•2х
4
= 1
1|
-г л
3
-г ^.л
4
- х-,
+
х-,
+
2х
А
= 3 .

ГЛАВА 4. ЛІНІЙНІ ПРОСТОРИ. ЕВКЛІДІВ ПРОСТІР
§1.
Лінійні простори. Підпростори
І. Короткі теоретичні відомості
Лінійні простори. Множина £ називається лінійним дійсним прос-
тором, якщо виконані такі умови:
1) існує правило, за яким будь-яким елементам х, у є £ ставиться
у відповідність елемент г = х
+
у є £, який називається сумою елементів;
2) існує правило, за яким будь-якому елементу х е £ та числу
аєК, ставиться у відповідність елемент г = ах є £ , який називаєть-
ся добутком елемента х на число а;
3) введені операції задовольняють наступним восьми аксіомам:
1.
х
+
у = у
+
х.
2.
(х
+
у)
+
2 = X
+
(у
+
2) .
3.
Існує елемент 0 є £, такий, що V хе £ х + 0 = х (елемент
0 називається нульовим).
4.
\/хє£ 3 елемент (-х)є £ , такий, що х + (-х) = 0 (еле-
мент -х називається протилежним).
5.
Ух є £ 1-х
=
х .
6. (сф)х = а(рх), а,рєК.
7.
а(х + у) = ах + ау , аєК.
8. (а + р)х = ах + рх, а,рєК.
Елементи лінійного простору називають також векторами та позна-
чають х, у,
2,....
Лінійний простір називається комплексним, якщо опера-
ція множення вектора на число визначена для комплексних чисел (а є С).
Система векторів х,, х
2
, ..., х
х
є £ називається лінійно залеж-
ною,
якщо знайдуться такі числа Я|, А
2
. •••
не вс
' рівні нулю, що
виконується рівність
(=1
У противному разі, коли вказана рівність має місце, якщо всі А.,- = 0,
/ = 1,5 , система векторів називається лінійно незалежною.

§1.
Лінійні простори. Підпростори
129
Упорядкована система векторів р = (є,,
е
2
,...,
е
п
) називається бази-
сом у лінійному просторі £, якщо
а) є X., к = 1, п ;
б) система векторів (є,, е
2
,..., е„) лінійно незалежна;
и
в) VЗс є X знайдуться такі числа
X,,
х
2
,..., х
п
, що
5с
= д;^ .
к=і
Ця формула називається розкладом вектора х за базисом Р, а коефі-
цієнти
Х|,
х
2
,...,
х
п
- координатами цього вектора у базисі Р.
Якщо Р = (еу,
е
2
,...,
е
п
) - базис лінійного простору £, то цей простір
називається п -вимірним та позначається Л
П
, а число п його вимірністю
і позначається п = аіт X .
Нехай Х„ -довільний п -вимірнийпростір, ^ = (е[,е
2
,... ,е
п
) -фіксо-
ваний базис у ньому. Тоді вектору х ставиться у відповідність стовпець
його координат у цьому базисі, тобто
Су \
х = ^х
і
е
і
<=> X =
(=1
х
2
Лінійні операції над векторами у координатній формі виглядають та-
ким чиним:
2 =х
+
у •» 2 = Х
+
¥,
у = Хх
<=>
У = ХХ.
Нехай р = (2
1
,е
2
,...,е„) та = (е[, ?
2
,
..-,?„),
два різні базиси у _£„ .
Кожний з векторів базису Р' розкладемо за базисом Р :
е'к = ЧкЧ + - +
1
пкЄ
п
<=>
Е
'к
Чк
у
1
пк;
Матрицею переходу від базису р до базису Р' називається матриця
Т =
де к -й стовпець є стовпець Е\ координат вектора е^ у базисі Р.

130
Глава 4. Лінійні простори. Евклідів простір
Якщо х - довільний вектор з Л
П
, X та X' - стовпці його коорди-
нат у базисах (3 та Я' відповідно, то має місце рівність:
Х = ТХ',
звідки
Х'
=
Т~
1
Х .
Це формули перетворення координат при зміні базису.
Підпростори. Підпростором лінійного простору X називається
підмножина X' с X, яка має властивості:
Г.х,ує£.' => х +
ує£.';
2°.
хє£' => ЛхеҐ \/Л.
Нехай 2 - довільна система векторів х
х
,
х
2
,...,
х
5
з лінійного
простору X.
Лінійною оболонкою системи 2 називається множина векторів
Ь(£>)
= | х | х = £
А,-
х,-, ї
(
єбД;єК, і = 1, *|.
/А Контрольні питання та завдання
1.
Що називається дійсним лінійним простором?
2.
Який лінійний простір називається комплексним?
3.
Яка система векторів називається лінійно залежною;
лінійно незалежною?
4.
Що називається вимірністю лінійного простору; базисом?
5.
Вказати вимірність та базис лінійного простору X,
якщо відомо, що у цьому просторі існує п лінійно незалеж-
них векторів е
х
,е
2
,... ,е
п
і будь-який вектор
X
є X лінійно
виражається через них.
6. Що називається розкладом вектора х лінійного прос-
тору £ за базисом е,,
е
2
,...,
е
п
? Що називається коорди-
натами вектора х у базисі }?
