Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


§1.
Лінійні простори. Підпростори
141
4.20. Знайти вимірність
та
один
із
базисів лінійного прос-
тору розв'язків системи:
а)
Х|
~1~
-3х
3
= 0;
б)
Х2
"і
-
х^
н~
х^
х^
—
0 у
0;
=
0.
Х|
"4"
ЗХ2
"^5
4лг,
+ 2х
2
- л:
3
+ 2х
4
- Х
5
4.21.
Знайти координати кожного
з
вказаних векторів
простору
РЗІХ) у
базисі
Х
2
,Х,1:
а) Зх
2
-2х
+
5;
б) 4х-1; в) (2х + 3)
2
.
4.22.
Знайти координати кожного
з
вказаних векторів
простору дійсних квадратних матриць другого порядку
у
базисі
Гі
0^
Г0
°)
(°
1>
Го
0^
.о
о,
,1
о У
ч°
о,
,0
К
а)
ґ-1 2
5
1
б)
Гз
_4
1
У задачах 4.23
-
4.25
у
довільному просторі
Х„
вектори
Е
П
і Х
задані своїми координатами
в
деякому базисі
р.
Довести,
що
система
Р'= (Е{, Е'
2
,..., Е'
П
) -
базис
у £„ та
знайти стовпець
X'
координат вектора
Х у
цьому базисі.
'Г1
гп
4.23.
Е[ =
1 1
2
,
х =
9
чі
А
чЧ
Г
2^
'
2
1
Г
6^
4-24.
Е
[ =
1
3
>
*3 =
-1
,
х =
2
4-24.
Е
[ =
ч-5,
ч
Ь
ч-7;
142
Глава 4. Лінійні простори. Евклідів простір
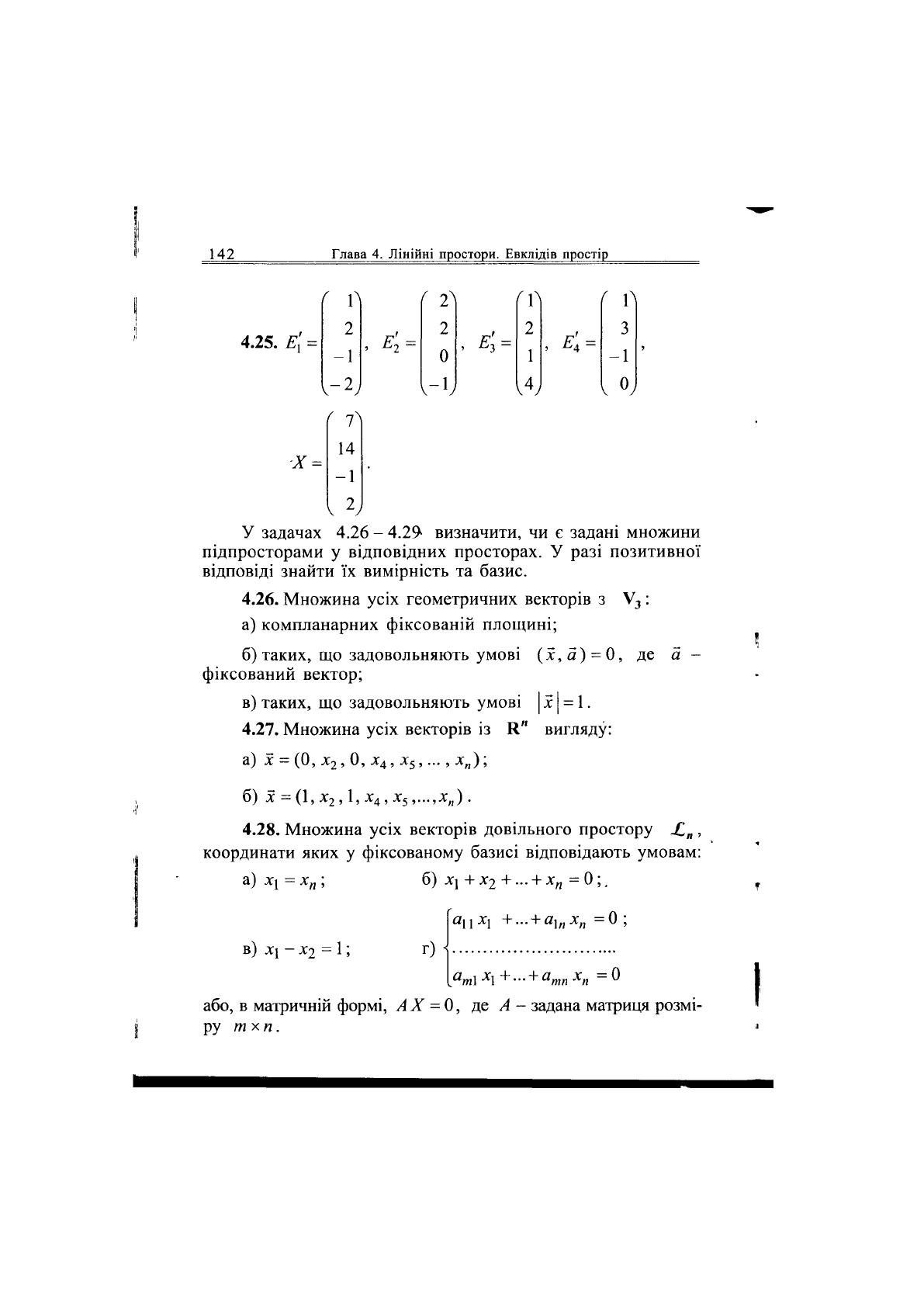
4.25. Е, =
Г 0
і л
2 2
2
г' -
3
-1 0
1
г' -
-і
,-2,
,4,
V о,
г
7
л
14
-1
V 2у
У задачах 4.26 - 4.29- визначити, чи є задані множини
підпросторами у відповідних просторах. У разі позитивної
відповіді знайти їх вимірність та базис.
4.26. Множина усіх геометричних векторів з У
3
:
а) компланарних фіксованій площині;
б) таких, що задовольняють умові (х,Й) = 0, де а -
фіксований вектор;
в) таких, що задовольняють умові
|
х
|
= 1.
4.27. Множина усіх векторів із К." вигляду:
а) х = (0, х
2
, 0, х
4
,
х$,...,
х
п
);
б) х =
(1,
х
2
,1,
х
4
, х
5
,...,х
п
).
4.28. Множина усіх векторів довільного простору £
и
,
координати яких у фіксованому базисі відповідають умовам:
а) хі = х
п
; б) х\ + х
2
+ ••• +
х
п
= 0 ;.
в) X} - Х2 = 1;
г)
а
п
х
х
+...
+
щ
п
х
п
= 0 ;
а
ті
х
і
+...
+
а
тп
х„ = 0
або,
в матричній формі, А X = 0, де А - задана матриця розмі-
ру ШУ.П.

§2,
Евклідів простір
143
4.29. Множина усіх матриць А порядку п , що відпові-
дають умовам:
т
а) А = А (симетричні матриці);
б) аеіЛ = 0.
4.30. Знайти вимірність лінійної оболонки Ь(х\, х
2
),
арифметичних векторів х
х
= (1, 0, 2,-1), Зс
2
= (0,-1,2,0).
Показати, що вектор х =
(1,
-1,
4, -1) належить до Ь{х
х
, х
2
).
У задачах 4.31 - 4.32 знайти вимірність та будь-який ба-
зис лінійної оболонки заданої системи арифметичних векторів:
4.31.
х, =(1,0,0,-1), х
2
=(2,1,1,0), х
3
=(1,1,1,1),
х
4
=(1,2,3,4), х
5
=(0,1,2,3).
4.32.
^ =(1,1,1,1,0), х
2
=(1,1,-1,-1,-1),
х
3
=(2, 2, 0,0,-1), х
4
=(1,1,
5, 5, 2), х
5
=
(1,-1,-1,
0, 0).
§2.
Евклідів простір
І. Короткі теоретичні відомості
Дійсний евклідів простір. Дійсний лінійний простір Л називається
дійсним евклідовим простором або евклідовим простором, якщо будь-яким
векторам х, у , що належать X, ставиться у відповідність дійсне число
(х, у) - скалярний добуток векторів, причому виконуються такі аксіоми:
1-
(х, у) = (у, х) ;
2.
(х
+
у, 2) = (ї, 1)
+
(у, г);
3.
(^ї, у) = Х(х, у),
А,
є К ;
4.
(х,х)>0, причому (х, х) = 0 о 5с = 0.
Позначення: Е - дійсний евклідів простір, Е„ - п -вимірний
дійсний евклідів простір.
Довжиною (нормою) вектора х називається число
| хІ
—
^(х^х) .
Якщо | х | = 1, то вектор х називається нормованим.
144
Глава 4. Лінійні простори, Евклідів простір
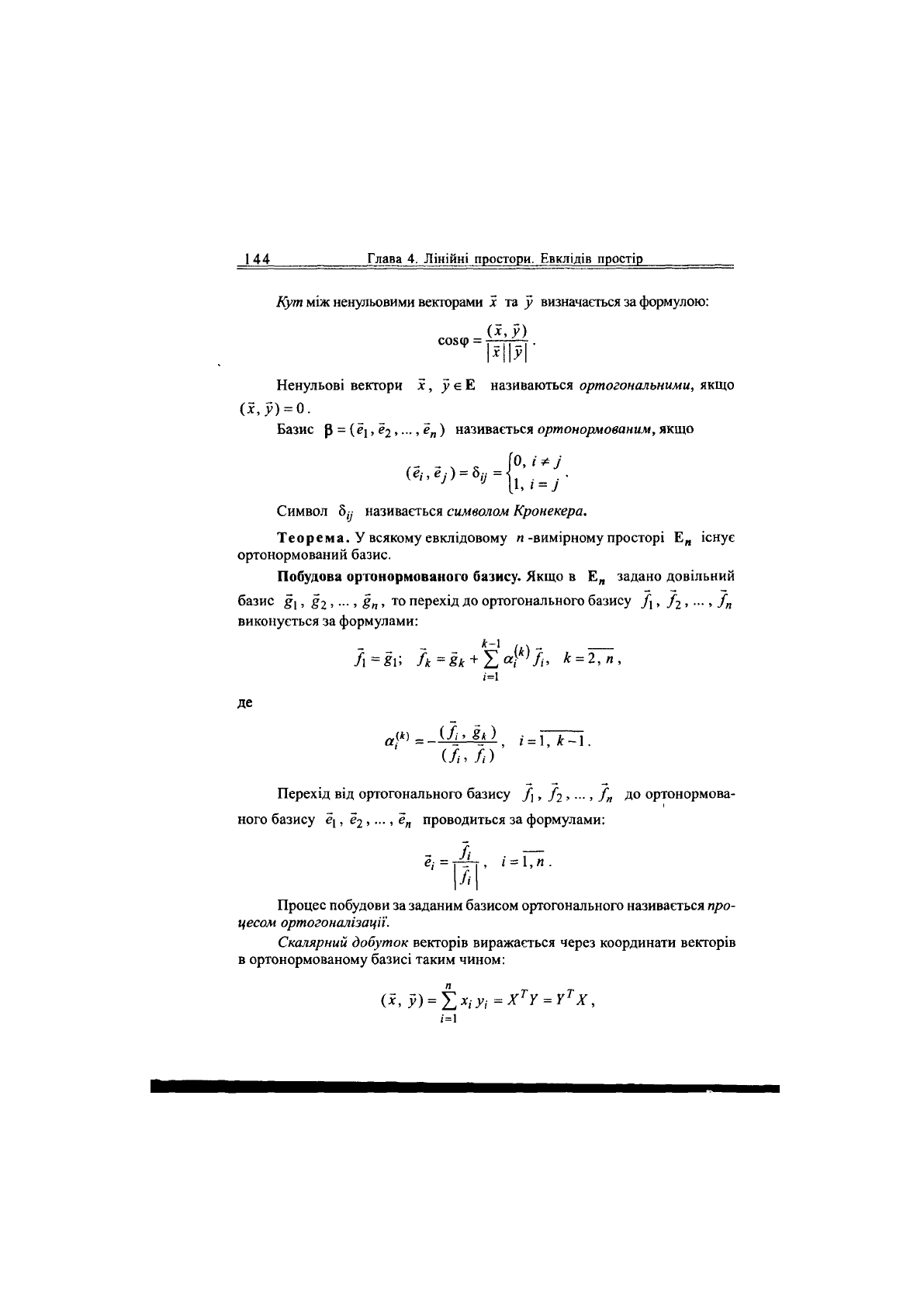
Кут між ненульовими векторами х та у визначається за формулою:
СОВф = . ' - .
I
х
\\У\
Ненульові вектори х, уєЕ називаються ортогональними, якщо
(зг,Л
=
о.
Базис В = (е\, е
2
,..., е„) називається ортонормованим, якщо
Символ б,-, називається символом Кронекера.
Теорема. У всякому евклідовому п -вимірному просторі Е„ існує
ортонормований базис.
Побудова ортонормованого базису. Якщо в Е„ задано довільний
базис §
1
, £
2
> •••
>
8п
>
то
перехід до ортогонального базису , /
2
,..., /„
виконується за формулами:
1=1
ДЄ
Перехід від ортогонального базису /], /
2
,..., /„ до ортонормова-
ного базису є,, е
2
,..., е
п
проводиться за формулами:
Є,=г4т,
/
=
Ї7Й.
Процес побудови за заданим базисом ортогонального називається про-
цесом ортогоналізації.
Скалярний добуток векторів виражається через координати векторів
в ортонормованому базисі таким чином:
(
х
, у) =
£
х
іУі=Х
т
¥
= У
т
Х,

§2.
Евклідів простір
145
де
х = (х
х
,...,х„) О Х =
, У = (У\,-,У„) <=>
у
=
Уп.
Довжина вектора визначається так:
\х\
=
л
](х,
х)
=
1
|Е
Х
|
2
•
Комплексний евклідів простір. Комплексний лінійний простір Л
називається унітарним або комплексним евклідовим простором, якщо
Ух,ує£ ставиться у відповідність комплексне число (х, у) - ермітів
добуток векторів, або скалярний добуток векторів у комплексному просторі,
причому виконуються такі аксіоми:
1-
У) = (У, х);
2.
(х
+
у, і) = (х, г)
+
(у, г);
3.
(Хх, у) = Х(х, у), Х,єС;
4.
(х, х) > 0, причому (х, х) = 0 <=> х = 0.
Позначення: V - унітарний простір, II „ - п -вимірний унітарний простір.
Зауважимо, що з аксіом 1 та 3 випливає, що (х, Ху) = ї.(х, у).
В унітарному просторі не вводиться кут між векторами. Однак решта
означень та результатів, сформульованих для дійсного евклідова простору,
справедливі і для унітарного простору.
Ермітів добуток векторів виражається через координати векторів в
ортонормованому базисі за формулою:
(х,
у)=^х
і
у
і
=Х
Т
¥
= ¥
Т
Х,
і=\
де
X]
х = (хі,...,х
п
) <=> Х =
, у = (уі,...,у
п
) о ¥ =
Уп

146
Глава 4. Лінійні простори. Евклідів простір
Довжина вектора визначається так:
(х[ = ^(х, х) = ^Х\Х\ + х
2
Хі + ... + х
п
X
II.
Контрольні питання
та
завдання
1.
Що називається дійсним евклідовим простором?
2.
Що називається довжиною (нормою) вектора х дійсного
евклідова простору Е ?
3.
Яка система векторів називається ортогональною?
4.
Яка система векторів називається ортонормованою?
5.
Що називається ортогоналізацією базису?
6. Записати формулу, за якою обчислюється скалярний добуток
векторів через їх координати в ортонормованому базисі.
7.
Записати формулу, за якою обчислюється довжина (норма)
вектора через його координати в ортонормованому базисі.
8. Дати означення комплексного евклідова простору (уні-
тарного простору).
9. Записати формулу, за якою обчислюється скалярний
(ермітів) добуток векторів через їх координати у ортонор-
мованому базисі унітарного простору.
10.
Записати формулу, за якою обчислюється довжина
(норма) вектора через його координати в ортонормованому
базисі унітарного простору.
///.
Приклади розв'язання задач
Приклад 1. В евклідовім просторі Е
2
в ортонормова-
ному базисі задано вектори х = (1, - 3), у =
(2,3).
Знайти
(х,у),
С05(х,у).
• Оскільки в просторі Е
2
скалярний добуток векторів х = (х) ,х
2
)
та у = {у\,у
2
) визначається рівністю (х, у) = х\у
х
+ х
2
у
2
, маємо
(х,Л = 1-2 + (-3)3 = -7.

§2,
Евклідів простір
147
За означенням
\
х
\\у\
а |х| = т](х, х) = ^х
2
+ х\ , отже
-7 -7
С08 (X, у) = = -== я -0,61 . <
7і
2
+(-3)
2
л/2
2
+3
2
^130
Приклад
2. В
евклідовім просторі
Е
3
за
даним базисом
8і'
82' Яз
побудувати ортонормований
базис.
£,=(1,-1,1), £
2
=(2,-3,4), £
3
=(2,2,6).
• Покладемо
7, =8\ =0,-1,1),
7
2
= §2 + «і
2)
7і,
де
„(2)_
(7і,І
2
)_ (1,-1,1)(2,-3,4)_ 2 + 3 + 4 _
(/і,/і)
3 3
Таким чином, 7г = (2, - 3,4) - 3 (1, -1,1) = (-1,0,1).
Далі знаходимо
7з=£з
+
°4
3)
7і+а
(
2
3)
7
2
,
ДЄ
„(3)_
ІЛіМА- (1,-1,1)(2,2,6)_ 2-2 + 6 _
1
(/і,/і)
3 3
„(3)
(7
2
,Із)_ (-1, 0,1) (2, 2, 6) _ -2 + 6 _
0
(/
2
,/
2
)
2 2
Таким чином, 7з = (
2
, 2,6) - 2 (1, -1,1) - 2 (-1,0,1) = (2,4,2).

148
Глава 4. Лінійні простори, Евклідів простір
Отримано /,=(1,-1,1), /
2
=(-1,0,1), /з =(2, 4, 2).
Перевірка показує, що ці вектори ортогональні
(/;,//)
= 0 , і, ] = 1, 3 ,
і* І-
Таким чином, вектори /,, /
2
, /з утворюють ортогональний базис.
Довжини цих векторів: |7}| = 7з, |/
2
| = 72, |/
3
| = 2л/б.
Пронормувавши вектори /,, /
2
, /з, отримаємо ортонормований
?• —
базис е,, е
2
, е
3
. Враховуючи, що е
і
= ^' , і - 1, 3, маємо:
І
/
І
_]_
1_
7з'
л/3' л/зі
е
2
=
V
-і-
о -±-
7Г 7Ї
, е
3
=
1 2 1
л/б'
л/б' л/б
Перевірка показує, що ці вектори ортогональні та нормовані, бо
(е
/
,Єу) = 0, ІФ), |е,| = 1, І,} = \,1.<
Приклад 3. В евклідовім просторі Е
3
задано базис
Є]=
(1,-1,0), е
2
=(0, 0, 2), е
3
=(-1, -1, 0). Перевірити,
що цей базис ортогональний та побудувати за цим базисом
ортонормований базис.
• Безпосередньо впевнюємося, що (є,-,
еу)
= 0, /, і = 1, 3, і ф і, тоб-
то заданий базис ортогональний. Щоб побудувати за даним ортого-
нальним базисом ортонормований базис, треба кожний базисний век-
тор пронормувати, тобто знайти вектори
I
?
1
Г
I
?
2
Г
І
?
3
Враховуючи, що |
?
2 | = 2, \е
3
1
= 72",
отримаємо
*1 =
>/2
' л/2
,0 ,е
2
= (0,0,1), ?з
ґ
-±
о
Л
72
'
72
'
-
шуканий базиси

§2.
Евклідів простір
149
Приклад 4. Вектори а та Ь задані в унітарному прос-
торі II
2
в ортонормованому базисі:
а=(2,
2-і), Ь=(3 + /, 2).
Знайти довжину |а | вектора а та ермітів добуток (а, Ь).
• \а\ =
^(а,а),
{а,а) = а
х
а\ + а
2
а
2
= 2
•
2 + (2-/) (2+ /) = 4+ 4 +1 = 9 ; |а| = 3.
(а, Ь) = а, \ + а
2
Ь
2
= 2(3 - /') + (2 - і)
•
2 = 6 - 2і + 4 - 2і =
10
- 4і. <
IV. Задачі для практичних занять
4.33.
Задані вектори в евклідовім просторі Е„ в орто-
нормованому базисі. Знайти довжини векторів х, у, скаляр-
ний добуток векторів, косинус кута
Ф
МІЖ
векторами, якщо:
а) х = (2,-1), у =
(0,-3);
б) х = (0,3,1), у = (-1,0,2);
в)
д=
= (5, 0,-12,0), ^ = (-3,1,0,2).
4.34. В евклідовім просторі Е
3
за даним базисом побуду-
вати ортонормований:
а) £,=(1,2,3), =
2
=(0,3,-2), яз =(0,1,-1);
б) £,=(1,2,3), #
2
=(0,2,0), £
3
=(0,0,3);
в) ^ =(1,0,0), #
2
=(0,1,-1), £
3
=(1,1,1).
4.35. В евклідовім просторі Е
4
за даним базисом побу-
дувати ортонормований:
а) £,=(1,1,0,0), £
2
=(0,0,1,1),
=
3
=(1,
0,1,1), £
4
=(0,1,0,-1);
б) £,=(1,0,1,2), £
2
=(-1,0,-1,0),
|
3
=(0,
0,2,1), £
4
=(0,1,1,1).
У задачах 4.36-4.38 застосувати процес ортогоналі-
зації до вказаних систем векторів у евклідовім просторі Е„ :

150
Глава 4. Лінійні простори. Евклідів простір
4.36. £,=(1,1,1,1), £
2
=(3,3,-1,-1), £
3
=(-2,0,6,8).
4.37. £,=(1,2,1,3), £
2
=(4,1,1,1), £
3
=(3,1,1,0).
4.38. £, =(1, 2, 2, -1), £
2
=(1,1,
-5, 3), £
3
=(3, 2, 8, -7).
У задачах 4.39 - 4.40 застосувати процес ортогоналізації
для побудови ортогонального базису підпростору, натягну-
того на задану систему векторів у евклідовім просторі Е„:
4.39. £,=(1,2,2,-1), £
2
=(1,1,-5,3), £
3
=(3, 2, 8,-7).
4.40. £,=(2,1,3,-1), £
2
=(7, 4, 3,-3), £
3
=(1, 1,-6, 0),
£
4
=(5,7,7,8).
У задачах 4.41-4.44 перевірити ортогональність вка-
заних систем векторів у евклідовім просторі Е
и
та допов-
нити їх до ортогональних базисів:
4.41.
е, =(1,-2,1,3), е
2
=(2,1,-3,1).
4.42.
еі =(1,1,1,1,1), е
2
=(1,0, 0,1,-2),
е
3
=(2,1,-1,0,2).
2 12) _ (12 2)
,333 /
2
^33 з)
4.44. е, = (1,1,1,2), е
2
=(1,1,
3,-3).
4.45. Задано вектори е,, е
2
, які утворюють ортонормо-
ваний базис унітарного простору. Знайти (5,6), якщо:
а) а =/е, + (г'-1)е
2
, 6 = (2-н')е, + (3 + /) е
2
;
б) 5 = 5е, -(3 + 4/)е
2
, 6 = Зіе
х
+(і-2)е
2
.
4.46. Задано вектори є,, е
2
, які утворюють ортогональ-
ний базис унітарного простору. Знайти (а, Ь), 6 якщо:
а) а = е, +(4 + г')е
2
, 6 = -2е, + (3
—
і)е
2
, |е,
|
= 2, |е
2
|
= 3 ;
, 1
4.43.
е, =
б) а
=
(1+і)е
1
+(2-і)е
2
, Ь=(1
+
і)е
1
+(2
+
і)е
2
,
Л.
е, =
