Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.


ГЛАВА 5. ЛІНІЙНІ ОПЕРАТОРИ
§1.
Алгебра лінійних операторів
І. Короткі теоретичні відомості
Основні означення. Нехай X лінійний простір. Якщо кожному
вектору х є X поставлено у відповідність єдиний вектор у є X , то
будемо казати, що задано відображення сА простору X в себе, або
оператор, перетворення, що діє в просторі X .
Коротко це записується так: ?А
:
X
—>
X , або у = с/і( х
),
або у = х.
Вектор у називається образом вектора х , а х - прообразом вектора у .
Оператор не обов'язково переводить елементи простору X в себе, він
може діяти, переводячи елементи одного простору в елементи іншого про-
стору. Будемо розглядати тільки оператори, що переводять елементи прос-
тору X в себе.
Лінійним оператором у лінійному просторі X називається будь-яке відоб-
раження сА: X
—>
X простору X в себе, що задовольняє таким умовам:
1)
сЛ(х
х
+х
г
)
=
сЛх
х
+
с
Лх
1
,
2) <А(Хх)=ХЛх,
де х, Х\, х
2
є X , X, - число.
Оператор 0 називається нульовим, якщо
0х=0 Ухе£.
Оператор £ називається тотожним (одиничним), якщо
£5с
= х V х є X .
Введені оператори є лінійними.
У п. III цього параграфа наведено приклади лінійних операторів та-
ких, як, оператор подібності, оператор дзеркального відображення, опера-
тор проектування, оператор повороту, оператор диференціювання та ін.
Матриця лінійного оператора. Нехай <А - лінійний оператор у
п -вимірному просторі Х„ і Р = (?|, е
2
, ..., е„ ) - деякий фіксований
базис. Розкладемо вектори Л е
к
за базисом Р :
<Ае
к
= а
]к
е
і
+а
2к
е
2
+...
+
а
Іік
е„,
к = \,п.

152
Глава 5, Лінійні оператори
Тоді матриця
ґ
а
и
а
Х2
...
а
Хп
*
а
2х
а
22
••• а
2п
А =
називається матрицею лінійного оператора А у базисі Р . Стовпці цієї
матриці складені з коефіцієнтів розкладу векторів А е
к
за базисом Р.
Лінійний оператор А у п -вимірному просторі £„ однозначно
визначається заданою матрицею, тобто:
у
=
Ах
<=>
У = АХ,
де X, У - стовпці координат векторів х, у, А - матриця оператора А
у базисі Р. Отже координати вектора у виражаються через координати
вектора х за формулами:
У\ =а
п
х
х
+а
п
х
2
+...+ а
и
,х„ ;
Уг =а
2х
х
х
+а
21
х
2
+...
+
а
2п
х
п
;
Уп =
а
п\
х
і+а„
2
х
2
+...
+
а
т
х„ .
Нехай А і А' - матриці оператора А у базисах р і р', а Т
- матриця переходу від базису р до базису р'. Тоді формула перетво-
рення матриці оператора при зміні базису має вигляд:
А'
=
Т~
Х
А Т.
Матриці А та А' називаються подібними.
Дії над лінійними операторами. Введемо наступні операції над
лінійними операторами, що діють у фіксованому просторі _С:
а) сумою операторів А та £ називається оператор С = А + ~В,
такий, що Сх =
(сА
+ Зд)х = Ах + Ш ,
б) добутком оператора А на число а називається оператор
С = а А, такий, що Сх = (а А)х =а А х,
в) добутком оператора А на оператор ІЗ називається оператор
С = А®,
такий,
що Сх = (АІЇ)х = А{іїх),
г) оберненим до оператора А називається оператор А~
х
, та-
кий, що А
А'
1
=
А~
Х
А =
\о
.

§1.
Алгебра лінійних операторів
153
Оператор А має обернений тоді і тільки тоді, коли його матриця А
невироджена. У цьому випадку оператор А називається невиродженим.
Ядро та образ лінійного оператора. Множина векторів х є £ , для
яких Ах = 0, називається ядром лінійного оператора А . Множина
векторів у = Ах, хе£, називається образом лінійного оператора
А або областю значень цього оператора.
Позначення:
Кет
А - ядро лінійного оператора А, ІтаА - об-
раз лінійного оператора А.
Ядро і образ лінійного оператора утворюють підпростори у просторі
£. При цьому вимірність ядра аіт Кег А називається дефектом опера-
тора А; вимірність образу штітс^ - рангом оператора А. Тобто,
йе1с^
= аітКегс^,
К&А
=
аіт Іт А .
Для п -вимірного простору £„ справедлива рівність
аітКегс^
+
аітІтс7?
= п .
II. Контрольні питання та завдання
1.
Який оператор називається лінійним?
2.
Які оператори називаються рівними?
3.
Що називається матрицею лінійного оператора про-
стору X у даному базисі?
4.
Записати формулу для знаходження матриці А'
лінійного оператора у базисі {є-}, якщо відомі матриця А
лінійного оператора Л у базисі {в,} і матриця Т перехо-
ду від базису {е/} до базису {є/}.
5.
Що називається сумою двох лінійних операторів? Чи
є ця сума лінійним оператором? Чому дорівнює матриця суми
двох лінійних операторів?
6. Що називається добутком двох лінійних операторів?
Чи є цей добуток лінійним оператором? Чому дорівнює мат-
риця добутку двох лінійних операторів?

1 54 Глава 5. Лінійні оператори
7.
Який лінійний оператор є невиродженим?
« 8. Який лінійний оператор називається оберненим да-
ному лінійному оператору?
9. Невироджений оператор <Л в деякому базисі зада-
ний матрицею А. Чому дорівнює в цьому базисі матриця
оператора, оберненого оператору
сА ?
10.
Що називається ядром лінійного оператора? Як воно
позначається?
11.
Що називається образом або областю значень
лінійного оператора? Як вона позначається?
12.
Що називається рангом оператора <А; дефектом опе-
ратора Л
?
13.
Як знайти ранг та дефект оператора
<А
; ядро опера-
тора
о4
; образ оператора
сЛ ?
///. Приклади розв'язання задач
У цьому пункті наведено 22 приклади розв'язання задач,
які за своєю тематикою розподілились таким чином:
1.
Доведення лінійності оператора: приклади 1-5.
2.
Знаходження матриці лінійного оператора з наведенням,
за можливістю, геометричної інтерпретації: приклади 6 -12.
3.
Знаходження матриці лінійного оператора та його об-
разу, а також матриця лінійного оператора у різних базисах:
приклади 13-16.
4.
Дії над лінійними операторами: приклади 17-20.
5.
Знаходження ядра та образу лінійного оператора:
приклади 21, 22.
Приклад 1. Довести, що наведені нижче оператори лінійні.
а) тотожний (одиничний) оператор £ такий, що
£ х = х Ух є X ;
б) оператор подібності сЯ такий, що
сАх =
ах, аєК, УхєХ.

§
1.
Алгебра лінійних операторів 15 5
• Згідно з означенням лінійного оператора перевіримо виконання умов:
1) А(х\ + х
2
) = А
х
х
+
А х
2
; 2) А (Ах) = ЛАх V х, х.\, х
2
є Л.
а)
(§
(х\
+
х
2
)
= х\ + х
2
= В х\ + £
^2 >
£(Л,х ) = Ях = Я<§х.
Умови 1), 2) виконуються, отже одиничний оператор лінійний.
б) А
(X,
+ х
2
) = а
(Х(
+ х
2
) = «
X)
+ах
2
—
Ах.\
+
Ах
2
,
А(Лх)=аЛх=Лах=ЛАх .
Умови 1), 2) виконуються, отже оператор подібності лінійний. А
Приклад 2. Оператор ^ у лінійному просторі _£ виз-
начено рівністю
сАх
=
х
+
а,
де а є X - фіксований вектор, а*
О-
Чи є оператор
<А
лінійним?
• Враховуючи, що
Ах=х+а, Ау=у+а, А(х
+
у )= х + у + а ,
маємо
А(х
+
у)фАх
+
Ау, бо х + у + а*х
+
а + у
+
а = х + у
+
2а.
Отже, умова 1) лінійності оператора не виконується і оператор А
не є лінійним. А
Приклад 3. Чи є лінійним оператор <А, якщо
V*"
є £
2
сАх
=
і-3]і
• Враховуємо, що
А
х,\
= і - 37 , Ах
2
=і-2>], А
(X]
+ х
2
) = / -
3
у .
Отже, с^Х!
+о?Зс
2
=2І -6_/
^ст?(
). Умова 1) не виконуєть-
ся.
Таким чином, даний оператор не є лінійним.
Приклад 4. Чи є лінійним оператор <А, якщо відомо,
що Ух є £
2
о4х = (пр
0>
,
Зс)у
.

156
Глава 5. Лінійні оператори
• Оператор буде лінійним у тому випадку, якщо виконуються умо-
ви 1) та 2) лінійності оператора. У нашому випадку
Л(х
х
+х
2
)={проу{х\+х
2
))і={»РОу
х
\
+ПРОу
Х
2
Ь =
= [проу х
х
)] + {проу х
2
)] = Лх
х
+ Лх
2
,
Л (X х )
=
(пр^ X х)_/' = X ( проу х)_/' = X Л х .
Таким чином, даний оператор є лінійним.
М
Приклад 5. Встановити, чи є лінійними наступні пере-
творення
сД,33,С,
якщо х = (х
х
, х
2
, х
3
),
є/І
X — ( Х| , Х| Х2
~Ь
Х^
$
4Х| Х^ )
5
^ X
—
(1, Х| ^2
"т"
Х^
;
4Х| Х2 ) )
С х — (Х|, х^ Х2 "Ь х^
9
4Х| Х2).
• Врахуємо, що х = (х
ь
х
2
, х
3
), у = (у\, у
2
, Уз)>
х
+
у = (х
х
+
у
х
, х
2
+
у
2
, х
3
+ уз ), Я х = (X
х
х
,
А х
2
, X х
3
).
Далі, для оператора Л : Лх = (х
х
, х
х
-х
2
+ х
3
, 4х
х
-х
2
),
с^(х + 35) = (х
1
+у
х
, х
х
+у
х
-(х
2
+у
2
)
+
х
3
+у
і
,4(х
х
+у
х
)~(х
2
+ у
2
)),
Лх
+
Лу=(х
х
+у
х
,х
х
+у
х
-(х
2
+у
2
)
+
х
3
+у
3
,4(х
х
+у
х
)-(х
2
+у
2
)).
Отже, Л(х
+
у) = Лх + Лу.
Л(Хх) = (Хх
х
, Хх
х
—
Хх
2
+ Ях
3
, 4Л.Х] -
Я
Х2 ),
X
Л х
=
X
(Х|,
х, - х
2
+ х
3
,
4х]
- х
2
) = (X Х|, X (х
х
- х
2
+
х
3
), X (4х] - х
2
)) ,
Отже, Л(Хх) = ХЛх.
Звідси випливає, що умови лінійності оператора Л виконані,
оператор - Л - лінійний.
Для оператора ІЗ: $>х = (1, X]-х
2
+х
3
, 4х]-х
2
),
®У = 0, у\ ~Уг +Уз>
4
У\ ~Уг) •
$(*
+ .У) = (1,
*1
+Л
~(*2
+
^2
) +
-"^3
+У3>
4
(
х
1 +Уі)~(
х
2 + 72)) ,
Ях + ®у = (2, х
х
+
у
х
-(х
2
+
у
2
)
+
х
3
+ у
3
, 4(х,
+л)-(х
2
+ ^2)) •

§1.
Алгебра лінійних операторів
157
Порівняння показує, що £(х + у)ф£х
+
33у. Отже, оператор Т>
не є лінійним.
•у
Для оператора С : С х =
(X],
х\ - х
2
+
х
3
,
4х[ -
х
2
),
Су = (уі, у\ -Уг + уз, 4у\ -у\)•
С{х
+
у
)=(х,
+у
{
, х, +у
х
-(х
2
+у
2
) + х
3
+у
3
,4(х
1
+у
1
)-(х
2
+у
2
)
2
),
С х
+
С у
=
(х, + уі, х, + у
х
- (х
2
+ у
2
) + х
3
+ у
г
, 4
(х,
+
Уі
) - (х\
+
у\ )).
Порівняння показує, що С{х + у)фСх
+
Су. Отже, оператор С
не є лінійним. Л
Приклад 6. Знайти матрицю тотожного оператора $ у
лінійному просторі Х„.
• Тотожне перетворення не змінює базисних векторів: £е) =е\,
<ре
2
=е
2
, $е„=е
п
,
тобто
\оЄ\
- \е\ +0е
2
+... +0е„ ;
\?е
2
= Оеі + 1е
2
+ ... + 0е„ ;
В е
п
= 0 Є\ + 0 е
2
+...
•+1
е
п
.
Отже, матрицею тотожного оператора є одинична матриця Е .
Ґ
1 0 ... 0
Л
0 1 ... о
Е =
0 0 1
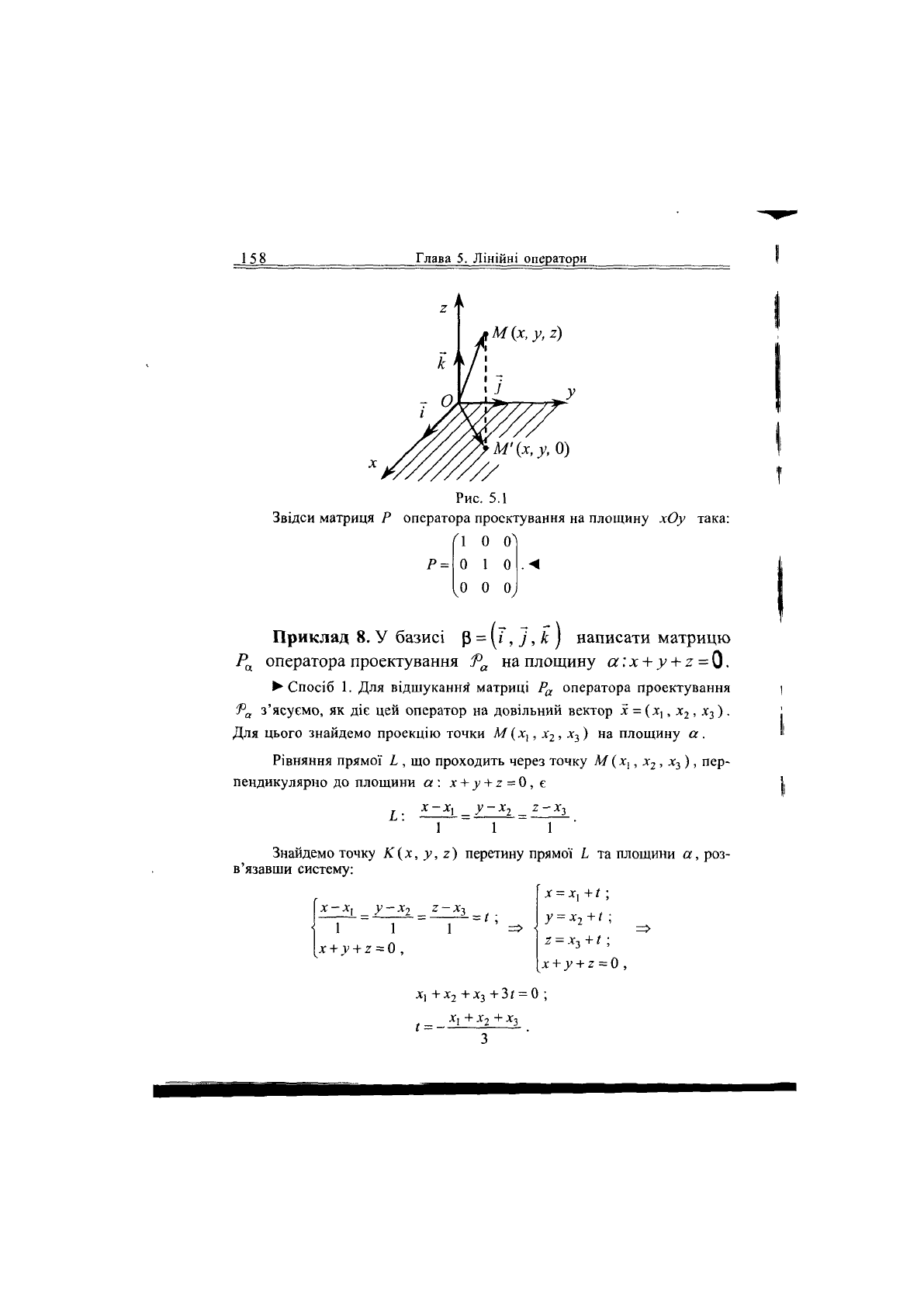
Приклад 7. Знайти матрицю Р оператора проектуван-
ня Я на площину хОу (рис. 5.1).
• Застосуємо оператор Р до базисних векторів /, /, к .
РЇ = І = (
1,0,0);
Я7=7
=
(0,
1,0);
Я£ = о = (о,о,о).
158
Глава 5.
Лінійні
оператори
М
(х,
у, 2)
М'(х,у, 0)
V/
Рис.
5.1
Звідси матриця Р оператора проектування на площину хОу така:
Гі 0 СЛ
Р =
0 1 0
0 0 0
Приклад 8. У базисі р = (і , }, к ) написати матрицю
Р
а
оператора проектування Р
А
на площину а:х
+
у
+
2=§.
• Спосіб 1. Для відшуканий матриці Р
а
оператора проектування
Р
а
з'ясуємо, як діє цей оператор на довільний вектор х = (х,, х
2
, х
3
).
Для цього знайдемо проекцію точки А/(х,, х
2
, х
3
) на площину а.
Рівняння прямої Ь , що проходить через точку М (х,, х
2
, х
3
), пер-
пендикулярно до площини а: х + у + г-0, е
І:
Х-Х)
1
У~х
2
1
2 -Х
3
Знайдемо точку К(х, у, 2) перетину прямої І та площини а, роз-
в'язавши систему:
X Х| у
—
1 і
Х +
у
+
2 ~о,
2-Х
3
•і ;
х
=
х, +1 ;
2 = х
3
4-
<
;
Х +7 + 2 =0 ,
X] + х
2
+ х
3
+ 3 ( = 0 ;
Х[ + х
2
+
х
3
* =
--

§1.
Алгебра лінійних операторів
159
Таким чином, х =
—
х.
У —
Хі ~г~ Х~\ Х-і .
з
1
з
2
з
3
2 = X,
Х-,
+
—Х
з •
Отже,
Я„3с
=
1
1 1 1 1
1
ЛІ
Х-і
Х-і
, Хі
Н
Х-> Хі , Хі Хл
Н
Х-і
з
з з з з з з з з
Знайдемо, як діє оператор Р
а
на базисні вектори.
я„7
2 _\_ _\_
З'
З' зі'
РЛ
І
1
з'
з'
П
з
І
_І
З 3 3
Звідси матриця Р
а
оператора проектування 'Р
а
така:
3 3 3
І
1 _!
3 3 3
1 1 2
з
з з;
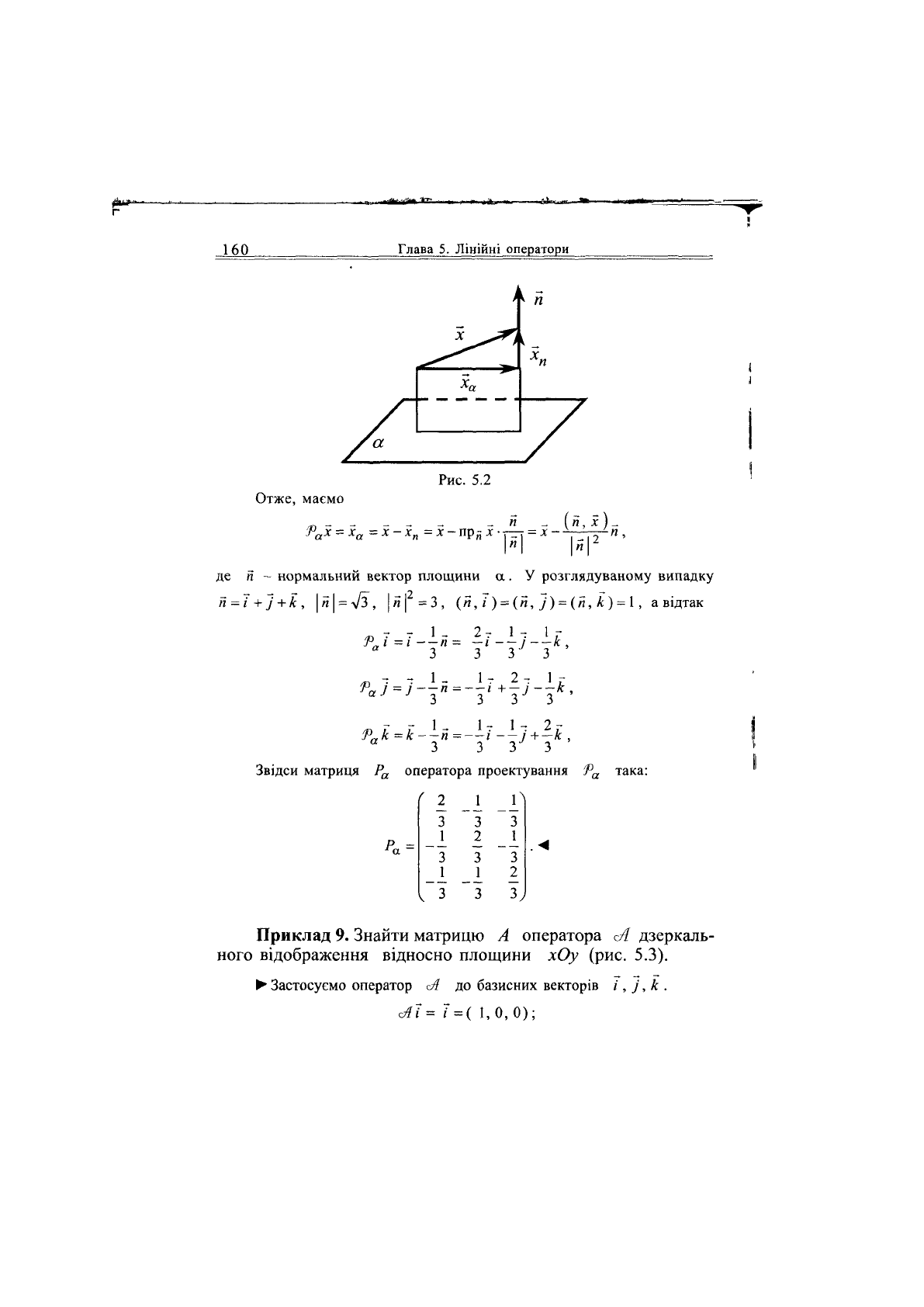
Спосіб 2. Оператор проектування на площину а визначається рівніс-
тю Р
а
х = х
а
, де х
а
- ортогональна проекція вектора х на площину а.
Ортогональною проекцією вектора х на площину а називається
вектор х
а
, компланарний площині а, причому різниця
х.
- х
а
пер-
пендикулярна цій площині, тобто (х-х
а
)±а (рис. 5.2). Отже,
_ п
Тут враховано, що х
п
повинно бути
напрямлено у бік вектора х . Тоді х
а
=х-х
п
.
160
Глава 5. Лінійні оператори
Отже,
маємо
Рис.
5.2
•^а
х
~~
х
а
—
X
Х
п
X пр^
= X
-
де Я - нормальний вектор площини а . У розглядуваному випадку
п =і
+
і + к, |Я| = л/з,
|Я|
2
=3,
(п, і ) = (п, і ) = (п, к) = 1, а відтак
Р„і = і п = —і — / — к ,
а
3 3 3 3
« ~ ~
1
- 1т 2 - 1 г
=7-^"
= -у'
+
з"-
/
~3
Т>„к=к
—п =—і —і
+
—к ,
а
3 3 3 3
Звідси матриця Р
а
оператора проектування Р
а
така:
( 2 _1_ _1_
л
3 3 3
1 2 1
З З
1 1
Приклад 9. Знайти матрицю А оператора
сЛ
дзеркаль-
ного відображення відносно площини хОу (рис. 5.3).
• Застосуємо оператор сА до базисних векторів /, }, к .
М = / =( 1, 0, 0);
