Тевяшев А.Д., Литвин О.Г. Вища математика у прикладах та задачах. Ч 1
Подождите немного. Документ загружается.

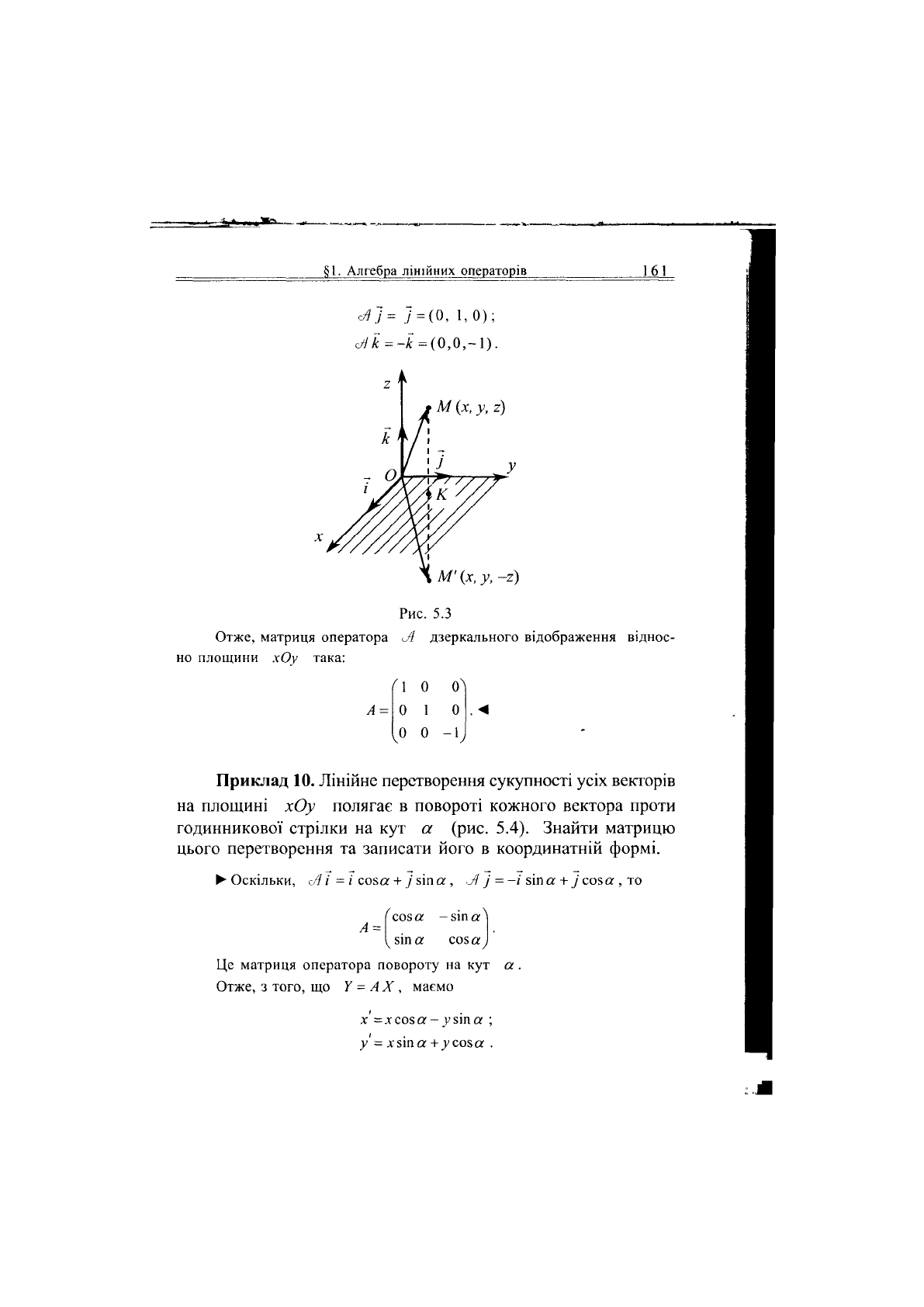
)1.
Алгебра лінійних операторів
161
<А} = 7=(0, 1,0);
Ак--к = (0,0,-1).
М (х, і/, г)
У, ~г)
Рис.
5.3
Отже, матриця оператора дзеркального відображення віднос-
но площини хОу така:
/
1 0 0
Л
0 1 0
,0 0 -1,
Приклад 10. Лінійне перетворення сукупності усіх векторів
на площині хОу полягає в повороті кожного вектора проти
годинникової стрілки на кут а (рис. 5.4). Знайти матрицю
цього перетворення та записати його в координатній формі.
• Оскільки,
<Л
і = і
сої
а + /' зіп а , А
_/
=
—і
зіп а + у соз а , то
А =
V
сова
кіп а
-зіп
а
соза
Це матриця оператора повороту на кут а .
Отже, з того, що ¥ = А X, маємо
х =хсо$а-узіпа ;
у = х$та
+
усоьа .
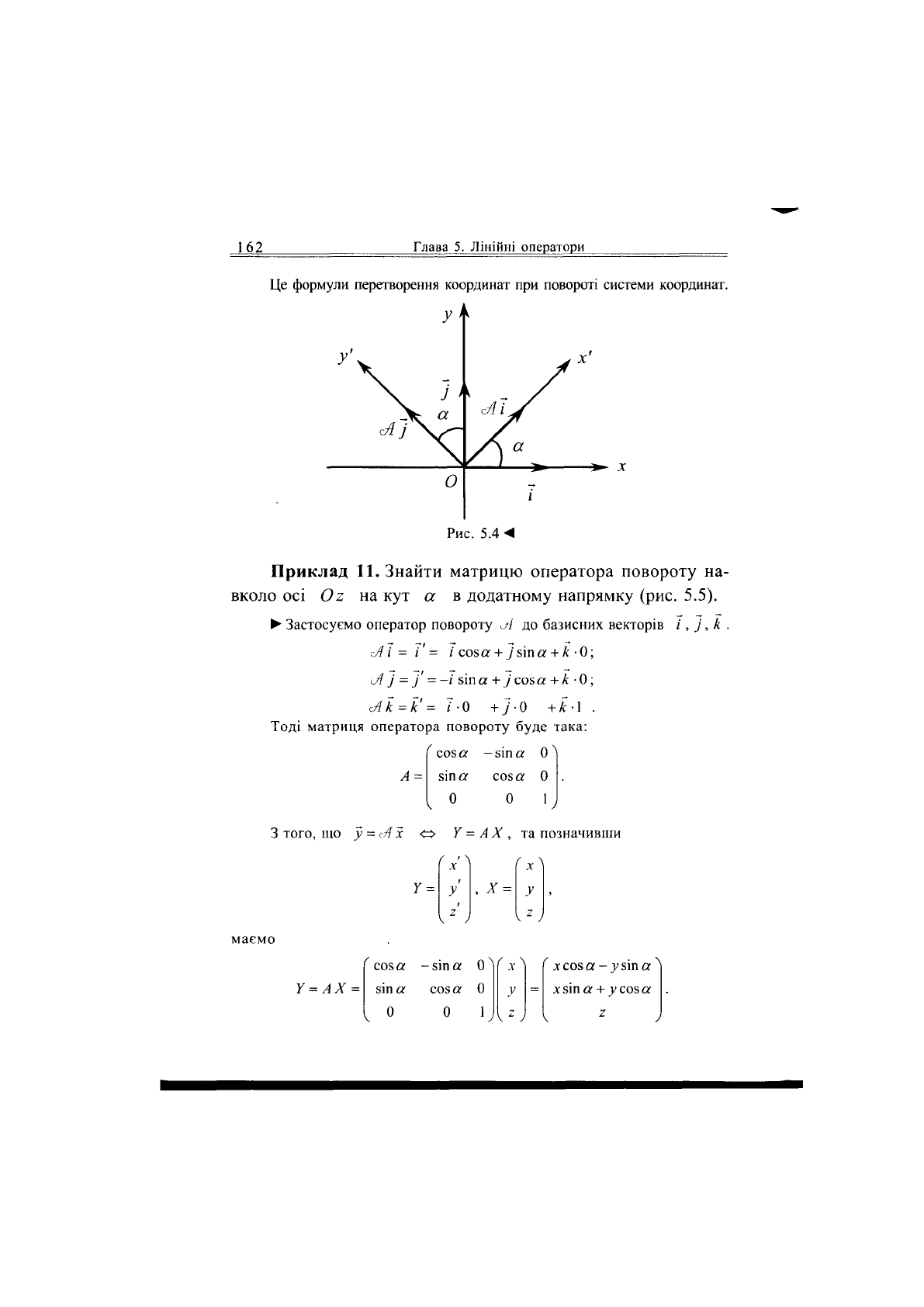
162
Глава 5. Лінійні оператори
Це формули перетворення координат при повороті системи координат.
х
Рис.
5.4
М
Приклад 11. Знайти матрицю оператора повороту на-
вколо осі Ог на кут а в додатному напрямку (рис. 5.5).
• Застосуємо оператор повороту Л до базисних векторів і, і, к .
Л і = і' = і соза + і зіп а + к
•
0;
Л) = і' = -/ зіпа + і соза + к
•
0;
Лк=к' = 1-0 +7-о +к-\ .
Тоді матриця оператора повороту буде така:
/—„~
-зіпа 0 ^
соза 0
А =
соза
зіпа
З того, що у = Лх <=>
¥ =
0 0
Ч
У
та позначивши
( ' >
X
У
, х =
У
1
7
V
" )
,
2
)
маємо
'соза -зіпа О^Гх^
¥ = АХ =
зіпа
0
соза 0
0 1
х соз а-у зіпа
х зіп а + у соз а
г

Рис.
5.5
Отже, х = хсоза - у$та ; у' = х зіп а + у соз а; г' = г.
Це формули перетворення координат при повороті навколо осі
О і на кут а.
М
Приклад 12. Знайти матрицю £> оператора диференці-
ювання О у просторі многочленів Р„ степеня <(л-1) у
базисі 1, і,
і
2
,...,
Ґ~
]
.
• Позначимо базисні вектори простору Р
п
е, =1, е
2
=і, е
3
=г
2
, ... , е„
=?""'.
Застосуємо оператор диференціювання до цих векторів.
?)е
1=
(1)'
= 0 = (0,0,0,...,0,0);
Ог
2
=(/)'
=
1
= Ц=(1,0, 0,...,0,0);
Юе
3
=((
2
)'
= 2і = 2е
2
=(0, 2, 0, ..., 0, 0);
:(/"-
1
)'
= (л-1)/"-
2
=(«-1)е„_
1
=(0,0,0,
.... л-1,0).
Отже, матриця оператора диференціювання
0 1 0 ... 0
Л
0 0 0
0 0 0
о
о
л-1
0

164
Глава 5. Лінійні оператори
Приклад 13. Знайти матрицю лінійного оператора сА
у базисі 5,= (1,0, 0), е
2
=(0,1,0),
е
3
=(0,0,і)
ЯКЩО ВІДОМО,
що цей оператор переводить будь-який вектор
х = (сс,, а
2
, а
3
) у вектор у = (3а ,, а
2
+а
3
, -а
3
).
• Знайдемо образи Л в\, Ле
2
, Л ?
3
базисних векторів. Згідно з умо-
вою х = «і
Є\
+
а
2
е
2
+
а
3
е
3
, тоді Л х =
3
а\ в\ + (а
2
+
а
3
)е
2
- а
3
<?
3
. Отже,
Ле\= Зе], Ле
2
=е
2
, Л е
3
= е
2
- е
3
. Запишемо координати образу кожно-
го вектора е\, е
2
, е
3
відповідно у стовпці матриці А . Тоді отримаємо
'З 0 0^1
А = 0 1
ч
0 0-1,
Це матриця оператора Л у даному базисі. ^
Приклад 14. Дана матриця
1 -1 2
2
1 0
0
0 5
лінійного оператора сЛ у базисі е,,е
2
,е
3
. Знайти сЯх,
якщо х = 2е| - е
2
+ Зе
3
.
• Спосіб 1. Відомо, що координати образу Лх та прообразу х
зв'язані співвідношенням ¥ = АХ, де У - стовпець з координат обра-
зу, А" - стовпець з координат прообразу. У нашому прикладі
-1
2
1
Ґ
2
)
(9\
У2
-
2 1 0 -1
=
3
0
5;
V
3
,
,15,
Таким чином, Лх =9е
х
+3е
2
+ 15е
3
.
Спосіб 2. Використовуючи означення матриці оператора Л у
базисі
Є],
е
2
, е
3
, маємо: Л е\=в\+ 2е
2
, Л е
2
= -е\ + е
2
, Ле
3
= 2е
х
+ 5е
3
.
Оскільки оператор <.// лінійний, то
Л х = Л (2 в\ - е
2
+
3
<?
3
)
= 2 е//
е\
- Л е
2
+ З
Л е
3
.

§1.
Алгебра лінійних операторів
165
Підставляємо Ле\, Ае
2
, Ле^ в останнє рівняння. Тоді знаходимо
Ах = 2(е, + 2 е
2
)-(-£?[ +е
2
)+3(2е
1
+ 5е
3
)
або
с7?х
= 9е
1
+3е
2
+15е
3
.-^
Приклад 15. У просторі £
4
розглядається лінійне перетво-
рення сЛ. Записати це перетворення в координатній формі, якщо
сА
е
х
= е
3
+
е
4
,
сА.е
2
=Є\+е
4
,
оАе
г
=е
х
+е
2
,
сЛ
е
4
= е
2
+ е
3
.
• Матриця перетворення А має вигляд:
Отже, з у = А х
Г°
1
1 0^
0 0
1 1
А =
1 0 0 1
,1 1
0
¥
=
--АХ
=>
{
У]Л
і
0 1
1 0^
(V
Уі
0 0 1 1
х
2
Уг
1 0
0 1
*3
\
1 1
0
о,
\х
4
)
Звідки у\ = х
2
+
х
3
, у
2
= х
3
+ х
4
, у
3
= х\ + х
4
, у
4
- X] + х
2
. <
Приклад 16. Дано два базиси
е
х
,е
2
та е[,е
2
лінійного
оператора сЛ у базисі
простору та матриця А =
е,, е
2
. Знайти
ч /
ги матрицю цього оператора у базисі е[,е'
2
, якщо
е,' = е, - е
2
, е
2
=3?, -4е
2
.
• Відомо, що якщо А - матриця оператора Л у базисі є,, е
2
, а Г -
матриця переходу від базису е,, е
2
до базису , е'
2
, то матриця Л' оператора
А у базисі е[,е
2
знаходиться за формулою А' =
Т~
Х
АТ.
У нашому випадку
7 =
і 3
Л
-І -4
4 3^
-І -І

166
Глава 5. Лінійні оператори
А'
=
Отже,
' 4 ЗУі
1 -1
3^
-4
6 17^1
-1 -2
Приклад 17. Перетворення Л полягає в повороті
кожного вектора площини хОу на кут а = —. Знайти в
4
координатній формі перетворення
сЛ
+ $ .
• Маємо
л/2 г л/2 -
сЛ 1—1 СОВ 1- / 81П — = 1 Н / ,
4
У
4 2 2 ^
,- -.71- К л/2 - л/2 -
А
1 = -1 81П —+ / соз — = / + / .
4 4 2 2
то
Отже,
Оскільки
2 2
72 л/2
2 2
0 1
А
+
Е =
4Ї
+
1
2 2
Таким чином, лінійне перетворення Л +8 в координатній формі
записується так:
4і Л
+і
, л/ї
X
V
, V =
Х
+
2 2
л/2"
+
1
Приклад 18. Нехай х =
(х,,
х
2
,
х
3
),
с7і*х
= (х, + х
2
,х
2
+ х
3
,Х]
+
х
3
),
33х = (х
2
+
х
3
,х,
+ х
3
, х, +
х
2
).
Знайти
сДЗЗх.
§1.
Алгебра лінійних операторів
167
• Випишемо матриці А та В операторів А та В відповідно.
^£,=(1,0,1), Ае
2
=(1, 1, 0), =(0,1,1);
£е,=(0,1,1), йе
2
=(1,0,1), і)е
3
=(1,1,
0).
(\ 1 0^ (0 1 п
А = 0 1
1
, в =
1 0 1
1
П
і о,
Знайдемо добуток матриць А та В .
(\ 1 2^
АВ= 2 1 1
Ь
2
К
Отже, оператор А
£>
мас матрицю А В .
у
=
ЛШ <=> У = АВХ.
У\ = X] + х
2
+ 2х
3
, у
2
=
2х| + х
2
+ х
3
, уі = X] + 2х
2
+
Х3
,
А £х =
(Х|
+х
2
+ 2х
3
, 2х, +х
2
+х
3
,
Х|
+2х
2
+ х
3
). А
Приклад 19. У просторі К
3
задано два лінійних оператори
ст?
і ІЗ. Знайти матрицю С лінійного оператора С =
оА£>- 1дЛ
та його явний вигляд у канонічному базисі К
3
, якщо
сАх =
(
2х
2
, - 2Х] + Зх
2
+ 2х
3
, 4х, - х
2
+ 5х
3
),
$>х =(-ЗХ] + х
3
, 2х
2
+х
3
, -х
2
+3х
3
).
• Оскільки
^=(0,-2,4),
Ае
2
=(2, 3,-і), Ае
3
=(0, 2,5)
та
то
8еі
=(-3, 0, 0),
Яе
2
={0,2,-і),
і^
3
=(і,1,3),
( 0 2
0^ ґ-3
0
А =
-2
3
2
5 = 0 2
І
,
4
-1
5,
V
0
-1
\

168
Глава 5, Лінійні оператори
Далі,
Тому
' 0
4
2
)
' 4
-7
5^
АВ = 6 4
1
•>
ВА = 0 5 9
,-12
-7
18,
-6
із,
( -4
11
"
3
1
С =
АВ-
В А = 6
-1 -2
г
26
-1
5,
За означенням матриці лінійного оператора у канонічному базисі
К" її стовпці є наборами компонент образів базисних векторів, отже
Се,
=(-4, 6,-26), Сг
2
=(П,-1,-і), Сез=(-3,-2,5).
Звідки знаходимо:
Сх=С(х,е, + х
2
е
2
+ х
3
е
3
) = х,Се, + х
2
Се
2
+ *зСе
3
=
= (- 4х, +11х
2
- 3*3 , 6х, -
дг
2
- 2^з , - 26х, - х
2
+
5хз ). ^
Приклад 20. Оператор сД у базисі є,, е
2
має матрицю
,. а оператор ІЗ у базисі е
х
= е, - е
2
, е
2
=е
х
+е
2
-
5 2,
матрицю 5 =
1 2
•2 З
Знайти матрицю оператора:
1) <Ал-$> у базисі е[,е'
2
; 2) с/1$ у базисі е
х
,е
2
.
• 1. Матриця £) оператора А + ІЗ у базисі , е
2
дорівнює сумі
матриць операторів А та ІЗ у цьому базисі. Оскільки оператор с#
задано матрицею Л у базисі є,, <?
2
, спочатку знайдемо матрицю С
цього оператора у базисі е{, е'
2
. Формула, що виражає залежність між
матрицями А та С оператора А відповідно у базисах е,, е
2
та е[, е'
2
,
має вигляд С = 7'
_1
^Г, де Т - матриця переходу від базису є,, е
2
до
базису е[, е
2
. Оскільки є, = е
х
- е
2
, е
2
= є, + е
2
, то Т = . . . Тоді
1 1
і
і і

§1.
Алгебра лінійних операторів
169
С = І
2
(
1 -1
1 1
З 1
5 2
1 1
•1 1
-0,5 -1,5
2,5 5,5
у
'-0,5
-1,5'
' 1
2
]
'0,5 0,5" '-0,5
-1,5'
+
'0,5 0,5"
, 2,5
5,5,
,-2
\
,0,5 8,5,
Таким чином,
о=с+в=
2.
Матриця Н оператора сАН у базисі е\, е
2
дорівнює А 5, де
5 - матриця оператора В у базисі е\, е
2
. Матрицю 5 знаходимо за
формулою 5 = 7Ї
_1
В7Ї, де Т\ - матриця переходу від базису е[,е'
2
до
базису е\, е
2
. Оскільки Т\=Т
-1
а 7, = Т.
то
8
=
Т~
1
Ґ
1
г
( 1
2
1
(\
-Г
2 3"
2
\
1
1
,-2
з,
,1
1
ч"
-1 2,
Отже
Н = А8 =
З 1
5 2
2
-1
2
'5 11
8 19
V
Приклад 21. Знайти ядро та образ лінійного оператора
сЛ
, який задано у деякому базисі е,, е
2
, е
3
матрицею
г
~\ 2 3^
1 1 0
0 3 3,
А =
V
=
0
• Ядро оператора - множина векторів простору, яка переводиться
оператором у нульовий вектор. Тому для знаходження ядра треба розв'я-
зати систему рівнянь А X = 0, тобто
'-\ 2 З
4
1 1 0
,озз,
де х\, х
2
, х
3
- координати вектора х у базисі е\, е
2
, е
3
.
Ранг матриці А отриманої однорідної системи дорівнює двом. Розв'я-
завши цю систему, отримаємо х\ = с, х
2
= -с , х
3
-
чином, ядром оператора А є:
Кегс^
= {(с, -с, с)
\
Усєк}.
аітКегг^ = л-К§Л = 3-2 = 1.
•
с Ус є К . Таким

170
Глава 5. Лінійні оператори
Базис Кег Л : Е
•
1
Образ оператора - множина образів усіх векторів даного просто-
ру у~Лх. Отже, якщо х\, х
2
, х
3
- координати у базисі ї\, е
2
, е
3
довільного вектора
самому базисі, то
х є X , У], у
2
, Уз
_
координати його образу у тому
(-і
2
3^
х
\
72
=
і
1 0
х
2
3
з^
^3,
або
V
Г2
Ч
'3^
Уі
1
х,+
1 х
2
+ 0
, о,
,3,
х
3
Ця рівність означає, що образ \тЛ збігається з лінійною обо-
лонкою системи стовпців матриці А , тобто за базис ІтЛ може бути
вибраний будь-який із базисів системи стовпців матриці А .
Оскільки
(
3
]
'
2
1
1
+
0 = і
,з,
та стовпці
м
1
>
0
ІЗ,
1
лінійно незалежні, то вони утворюють базис \тЛ .
Таким чином, образом оператора Л є:
1тст? = {с
1
(-1,1,0) + с
2
(3,0,з)| Ус,,с
2
єК},
сіітіте// =
2 .
Г-Г
Базис ІтЛ : Е
х
=
1
. Е
2
=
0
, °,
V
3
,
