Турунтаев Л.П. Теория принятия решений
Подождите немного. Документ загружается.


91
Найти оптимальную стратегию, обеспечивающую макси-
мальный средний доход.
Воспользуемся критерием Байеса:
1
2
3
( , ) 100 0,4 25 0,3 80 0,1 64 0,2 68,3;
(, ) 78;
(, ) 62.
Bpx
Bpx
Bpx
=⋅+⋅+⋅+⋅=
=
=
Лучший результат дает альтернатива
2
x .
Рассмотрим измерение предпочтения альтернатив в поряд-
ковой шкале, осуществляемое методами ранжирования или пар-
ного сравнения. Пусть результаты измерения предпочтений бу-
дут представлены в виде матриц парных сравнений альтернатив
в каждой ситуации с элементами
k
ij
x
, где ,1,ij m= — сравни-
ваемые альтернативы
i
xX
∈
и
;
j
xX
∈
1,kn=
— оцениваемые
ситуации
k
e
åñëè
åñëè
1, ;
0, .
kk
ij
k
ij
kk
ji
xx
x
xx
=
f
f
Совокупность матриц парных сравнений (равно числу си-
туаций) можно рассматривать как точки в пространстве упоря-
дочения решений. В этом пространстве можно ввести понятие
«средней точки» (средней матрицы парных сравнений) с коор-
динатами
ij
y .
Для построения средней матрицы парных сравнений вос-
пользуемся условием минимума суммарного расстояния этой
матрицы от матриц парных сравнений для всех ситуаций [6].
2
11 1
()min,
ij
nmm
k
kij ij
y
ki j
px y
== =
−→
∑∑∑
где
k
p — вероятность ситуации
k
.
Раскроем скобки и упростим выражение, минимизируемое
по
ij
y

92
() ( )
2
2
1, 1 1, 1
1, 1 1, 1
2() 2
1
2 .
2
nm nm
kk kk
k ij ij ij ij k ij ij ij ij
kij kij
nm nm
kk
k ij k ij ij
kij kij
px xy y px xyy
px py x
== ==
== ==
−+ = −+=
=− −
∑∑ ∑∑
∑∑ ∑∑
При заданных матрицах парных сравнений
k
ij
x
первый член
в этом выражении является постоянным. Поэтому необходимо
максимизировать
L
,1
1
max.
2
ij
mn
k
ij k ij
y
ij k
Lypx
=
=−⇒
∑∑
Максимальное значение
L
достигается при
1
1
åñëè
åñëè
1
1, ;
2
1
0, .
2
n
k
kij
k
ij
n
k
kij
k
px
y
px
=
=
≥
=
<
∑
∑
Средний выигрыш альтернативы определяется по формуле
1
11
, 1, .
m
ij
j
i
mm
ij
ij
y
im
y
=
==
β= =
∑
∑∑
Наилучшей альтернативой считается arg max .
j
i
i
x
∗
=
β
Пример
Пусть результаты предпочтений альтернатив в каждом со-
стоянии внешней среды представлены (по данным табл. 5.1) в
виде матриц парных сравнений
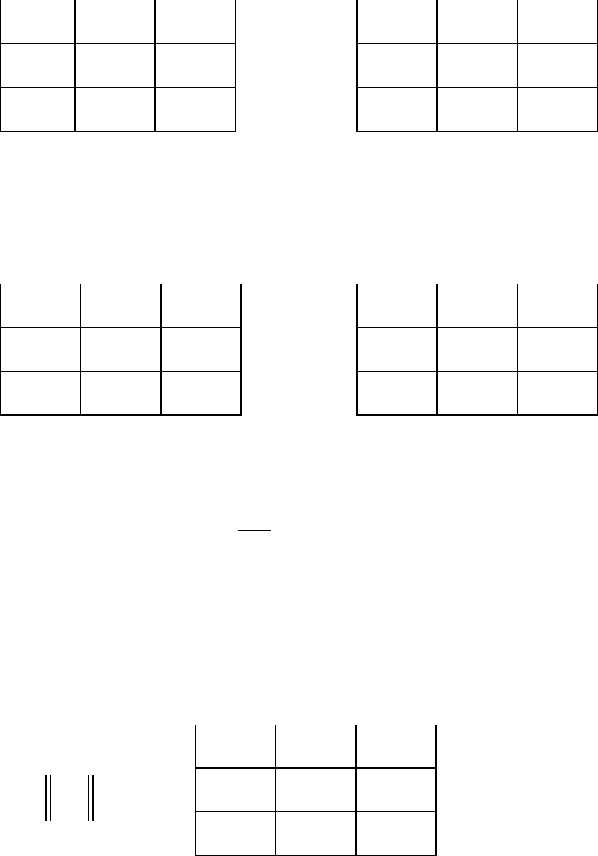
93
Определяем элементы средней матрицы предпочтений аль-
тернатив. В ней
1, 1, 3,
ii
yi==
12
{
10,4 00,3 10,1 00,2 0,4 0,1 0,5
}
1.y =⋅ +⋅ +⋅ +⋅ = + = =
Результаты расчетов будут следующими
Наилучшими альтернативами следует считать
1
x
∗
и
2
x
∗
.
5.2.3 Критерий минимума дисперсии оценочного
функционала
Пусть
22
1
(, ) [ (, )]
m
i i ij ij i i
j
px p y B px
=
δ= −
∑
.
Оптимальная стратегия
k
x
∗
выбирается исходя из условия
4,0:
11
=pe
1
x
2
x
3
x
1
x
1 1 1
2
x
0 1 1
3
x
0 0 1
3,0:
22
=
pe
1
x
2
x
3
x
1
x
1 0 0
2
x
1 1 0
3
x
1 1 1
1,0:
33
=pe
1
x
2
x
3
x
1
x
1 1 1
2
x
0 1 0
3
x
0 1 1
2,0:
44
=
pe
1
x
2
x
3
x
1
x
1 0 1
2
x
1 1 1
3
x
0 0 1
ij
y =
1
x
2
x
3
x
1
x
1 1 1
2
x
1 1 1
3
x
0 0 1
1
2
3
3/7
3/7
1/7
β=
β=
β=

94
2
arg min ( , )
kii
i
xpx
∗
=δ.
Решение характеризуется минимальным разбросом «полез-
ности» относительно ее математического ожидания.
Пример
Исходные данные приведены выше в табл. 5.1.
2222
1
2
( , ) 0,4(100 68,3) 0,3(25 68,3) 0,1(80 68,3)
0,2(64 68,3) 981,81;
i
pxδ = −+−+−+
+−=
2
2
(, ) 714;
i
pxδ=
2
3
(, ) 456.
i
pxδ=
Лучший результат дает альтернатива
3
x
.
Данный критерий используется дополнительно при одина-
ковых средних доходах, найденных по критерию Байеса. Если
решение реализуется однократно, то понятие среднего дохода
теряет смысл. В этом случае для ЛПР более привлекательной
может оказаться альтернатива, обеспечивающая максимальную
вероятность того, что доход будет не менее некоторого, до-
пустимого минимума.
5.2.4 Критерий максимума уверенности в получении
заданного дохода
Зафиксируем величину
α
, удовлетворяющую неравенствам
12
α<α<α, где
12
min min ; max max .
ij ij
ij
ij
yyα= α=
Будем рассматривать
α
как некоторый порог, ниже которо-
го уменьшать полезность нецелесообразно. Обозначим
,i
E
α
—
множество состояний внешней среды, при которых обеспечива-
ется выполнение неравенства
ij
y ≥α
.
,
()
ijiji
j
Eeyx
α
=≥αU
.
Вероятность выполнения этого неравенства при условии
использования стратегии
i
x :
,
,,
()() ,
ji
iiji ji j
eE
P
Py x Pe E p
α
αα
∈
=≥α=∈=
∑

95
2
∗
x
при
где
j
p
— вероятность наступления события
j
e
.
Оптимальная стратегия определяется условием
arg max ( )
kiji
i
xPyx
∗
=≥α.
Пример
Исходные данные приведены в табл. 5.1. Оценим влияние
величины порога на оптимальность стратегии.
Возьмем порог
80α>
. Вероятность выполнения этого не-
равенства:
а) для стратегии
1,1 11
(80) 0,4
ij
xPy xp
α
→>==;
б) для стратегии
2,24
0,2 ;xP p
α
→==
в) для стратегии
3,32
0,3xP p
α
→==
.
Оптимальной стратегией для
80
α
> будет
1
x .
Пусть
30α> , тогда
1,1 1134
2,2 1124
3,3 1123
(30) 0,7;
(30) 0,9;
(30) 0,8.
ij
ij
ij
xp Py xppp
xPPy xppp
xPPy xppp
α
α
α
→= > =++=
→= > =++=
→= > =++=
Оптимальной будет
2
x и так далее.
Если исследовать диапазоны порогов, то получим опти-
мальные стратегии со следующими диапазонами:
1
x
∗
при
,1 ,2 ,3
èëè80 100 ( 0,4; 0,2; 0,3 0)PP P
αα α
<α ≤ = = =
;
,2 ,1 ,3
,2 ,1 ,3
30 70 ( 0,9; 0,7; 0,8),
100 120 ( 0,2; 0);
PPP
PPP
ααα
ααα
<α ≤ = = =
<α ≤ = = =
3
x
∗
при
,3
30 1P
α
α≤ =
.
5.2.5 Модальный критерий выбора альтернатив
Сущность модального критерия выбора альтернатив состо-
ит в том, что ЛПР при выборе альтернативы ориентируется на
наиболее вероятное состояние среды.

96
Пусть максимум распределения вероятности приходится на
состояние среды
l
e
, т.е. max .
lj
j
pp
=
Тогда оптимальное реше-
ние
k
x
∗
находится из условия (,)max
kl il
i
F
xe y
∗
= .
Если имеется несколько состояний среды, которым соответст-
вуют одинаковые максимальные вероятности
{
}
1 2
, , ...,
j
jjr
ll l
,
то альтернатива выбирается таким образом, чтобы обеспечить
максимум среднего значения оценочного функционала по всему
множеству наиболее вероятных состояний:
11
11
(, )max
rr
kjl ijl
i
ll
F
xe
y
rr
∗
==
=
∑∑
.
Достоинство модального критерия состоит в значительном
сокращении объема расчетов.
5.3 Принятие решений в условиях
неопределенности
5.3.1 Принятие решений при линейной упорядоченности
состояний внешней среды
ЛПР не знает закона распределения вероятностей состояний
внешней среды, но располагает информацией, позволяющей
упорядочить эти состояния по вероятности их появления.
Последовательность принятия решения в рассматриваемой
ситуации описывается следующим алгоритмом.
Шаг 1. Установить отношение порядка
1
E на множестве Е
состояний внешней среды.
Шаг 2. Найти точечную оценку распределения вероятно-
стей состояния внешней среды, т.е. некоторое конкретное рас-
пределение
0
1
( , ..., )
n
pp p= , удовлетворяющее введенному на
первом шаге отношению порядка
1
E
.
Шаг 3. Для найденной точечной оценки найти оптималь-
ную альтернативу по одному из критериев (или их группе), ис-
пользуемых для ПР в условиях риска.

97
Шаг 4. Проверить, является ли найденное решение опти-
мальным для всех других распределений
0
pp
≠
, но удовлетво-
ряющих данной системе отношений порядка
1
E . Если «да», то
решение принимается, иначе — перейти к следующему шагу.
Шаг 5. Наложить на распределение
0
p дополнительные ус-
ловия (их характер рассмотрен ниже) и проверить их выполне-
ние. Если эти условия выполнены, то решение принимается,
иначе — ввести дополнительные отношения порядка в
1
E и вер-
нуться к шагу 2.
Рассмотрим алгоритм более подробно.
На
шаге 1 ЛПР устанавливает отношение порядка на мно-
жестве
Е. Простейший способ упорядочения — введение на
множестве
Е отношения предпочтения следующим образом:
; , ; ,
j
kjkjk j
ee ppeeEp⇔≥ ∈f
где
k
pp∈ — вектор распределения вероятностей внешней сре-
ды;
j
p
— вероятность появления состояния
j
e
. Если такое упо-
рядочение выполнено для всех пар (
,)
j
k
ee
, то получаем линей-
ное отношение частичного порядка и будем считать, что состоя-
ния внешней среды перенумерованы таким образом, что
12
...
n
pp p≥≥≥
.
Шаг 2. Вычисление точечных оценок распределений веро-
ятностей, удовлетворяющих введенным отношениям порядка,
может быть выполнено различными способами. Один из них
предложен П. Фишберном. Оценки Фишберна
j
p
образуют
убывающую арифметическую прогрессию вида
2( 1)
, 1, .
(1)
j
nj
p
jn
nn
−
+
==
+
Другие способы можно найти в работе [30].

98
Шаг 3. Находим оптимальную альтернативу, например, по
критерию Байеса:
1
max ( , )
n
ijij
i
j
Bpx p
y
=
=
∑
. Пусть это критерий
k
xx
∗
= при альтернативе
.k
1
(, ) max
n
kjij
i
j
Bpx p
y
=
=
∑
.
Шаг 4. Необходимо проверить, будет ли
k
x оптимальным
решением не только для найденного распределения
j
p
, но и для
любого другого распределения, удовлетворяющего введенному
на шаге 1 отношению порядка
1
E .
При использовании критерия Байеса
,
ki
xxi∀f можно га-
рантировать тогда и только тогда, когда
((, ) (, ) 0
ki
Bpx Bpx−≥
или
1
()0
n
jkj ij
j
py y
=
−
≥
∑
для всех i, ,pP∈
(5.1)
где
Р — множество распределений, удовлетворяющих заданно-
му отношению порядка
1
E .
Очевидно, что для выполнения (5.1) необходимо и доста-
точно, чтобы
1
min ( ) 0, 1,
n
jkj ij
p
j
p
yy
im
∈Ρ
=
−≥ =
∑
. (5.2)
Поскольку выражение
pP
∈
представляет собой в рассмат-
риваемом случае не что иное, как систему линейных ограниче-
ний, накладываемых на компоненты вектора
Р, то выражение
(5.2) определяет множество задач, состоящее из
(1)m − задач
линейного программирования (при
ik
=
условие 5.2 выполня-
ется).
Шаг 5. Этот шаг и последующие удобнее рассмотреть на
примере.
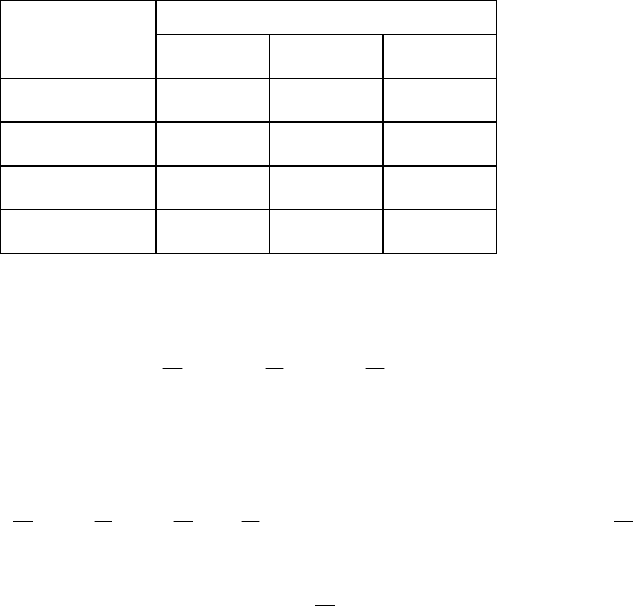
99
Пример
Пусть таблица значений оценочного функционала задана
(табл. 5.2). Предположим, что на первом шаге алгоритма на
множестве состояний среды
123
{
,,
}
Eeee
=
введено отношение
частичного порядка с помощью неравенств
123
,pp p≥≥
123
1.pp p
+
+=
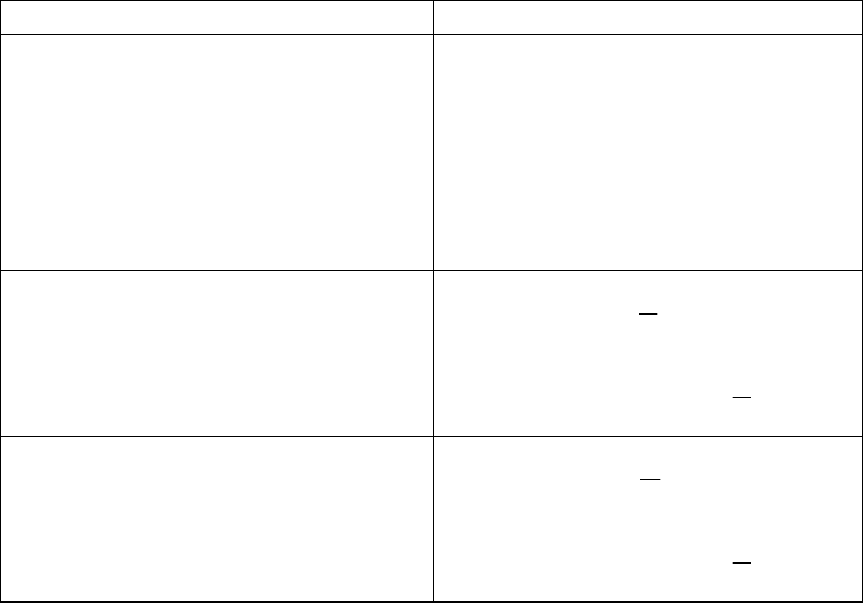
Таблица 5.2 — Исходные данные
Вычислим по формуле Фишберна точечные оценки:
123
111
; ; .
236
ppp===
Для выбора оптимальной стратегии воспользуемся крите-
рием Байеса. Математическое ожидание полезностей
123
4
1111 1
(, ) 8 2 4 5; (, ) 6; (, ) 5;
2363 6
5
( , ) 3 .
4
Bpx Bpx Bpx
Bpx
=⋅ +⋅+⋅ = = =
=
Наилучшей стратегией по Байесу является стратегия
2
x .
Проверим, для любого ли распределения вероятностей,
удовлетворяющего заданному отношению порядка, эта страте-
гия оптимальна.
2 i
xxf
для всех альтернатив i, кроме второй, на любых до-
пустимых распределениях вероятностей, если
121 1 222 2
23 3
min[ ( ) ( )
()]0, {1,3,4};
iii
i
Lpyypyy
yy i
=−+−+
+− ≥∈
(5.3)
Стратегии Состояния среды
1
e
2
e
3
e
1
x
8 2 4
2
x
6 7 4
3
x
4 7 5
4
x
3 4 6
100
123
123
;
1.
pp p
pp p
≥≥
+
+=
Таким образом, мы имеем 3 задачи линейного программи-
рования (табл.5.3).
Таблица 5.3 — Задачи линейного программирования
Условие задачи Решение
0,,
1
0
0
min052
321
321
32
21
3211
≥
=++
≥−
≥−
→⋅++−=
ppp
ppp
pp
pp
pppL
0
1
2
32
1
min1
==
=
−=
pp
p
L
min2
313
→
−
= ppL
ограничения те же
3
1
3
1
321
min3
===
=
ppp
L
min233
3214
→−+= pppL
ограничения те же
3
1
3
4
321
min4
===
=
ppp
L
Как видно из табл. 5.3, условие 5.3
0
i
L ≥
выполняется
только для стратегий
3
x и
4
x , но не для
1
x . Следовательно, ре-
шение
2
x , полученное на основе точечных оценок Фишберна,
лучше, чем
3
x
и
4
x
,
2324
ïðè(, )xxxx p∈Ρff
, но
21 1 2
åñëè , 2 5 0xx p p
−
+≥f — это дополнительное ограниче-
ние. Оно не противоречит ранее введенной системе ограничений
(есть общая область допустимых решений и при этом условии).
Если ЛПР считает, что последнее ограничение выполняется
(а это так), то
2
x оптимальна для любого распределения вероят-
ностей, которое может иметь место. Если бы ограничение не
выполнялось (т.е. не было общей области допустимых реше-
