Турунтаев Л.П. Теория принятия решений

Подождите немного. Документ загружается.

101

ний), то в рассмотрение вводится дополнительное отношение —

52pp≤

(но не

52pp≥

, а) и переходим на шаг 2.

5.3.2 Принятие решений при отсутствии информации

о состоянии внешней среды

ЛПР не располагает никакой информацией о вероятностях

появления различных состояний внешней среды

, в том числе

и об их соотношении.

Простейший способ решения задачи

состоит в использовании точечных оценок неизвестного апри-

орного распределения, причем критерии выбора в таких услови-

ях принимают известный «принцип недостаточного основания»,

предложенный Даниилом Бернулли, и означают, что если нет

данных, позволяющих считать одно состояние среды

e ∈Ε

бо-

лее вероятным, чем любое другое, то априорные вероятности

всех этих состояний следует считать равными

Оптимальной по критерию Бернулли—Лапласса считается

альтернатива, максимизирующая математическое ожидание по-

лезности, т.е.

(, ) max (, ) max( )

iij

Bpx Bpx y

∗

∑

Способ, использующий понятие Байесова множества

Рассмотрим множество всевозможных распределений веро-

ятностей состояний внешней среды. Так как

∑

, то в каж-

дом распределении достаточно задать лишь (1)n

−

вероятность,

например,

, ..., .

−

Обозначим

( , ..., )

pp p

−

= . Очевидно, что каждому кон-

кретному распределению вероятностей соответствует

точка

(1)n − -мерного пространства с координатами

, ...,

−

, ле-

жащая в замкнутой области, определяемой соотношениями:

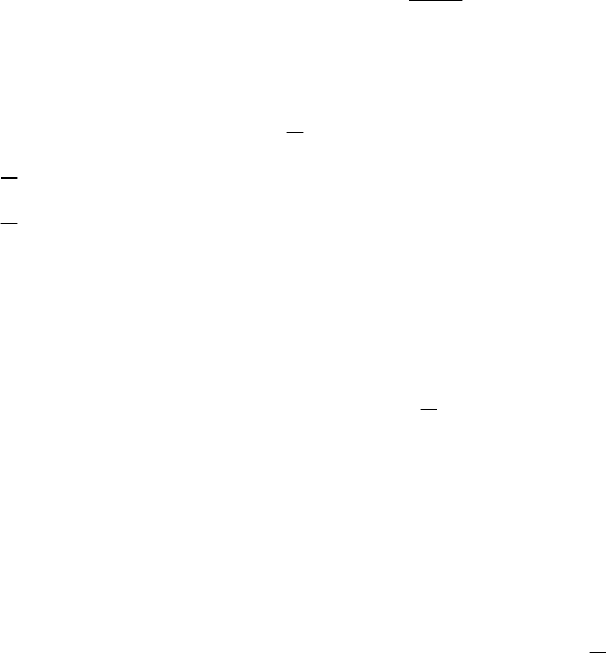
102

0, 1, 1 , 1

pjn p

−

≥=− ≤

∑

Область, определяемая таким образом, называется (1)n − -

мерным симплексом

−

. Если n = 2, то одномерный симплекс

— это отрезок [0,1], если m = 3, то двумерный симплекс

— треугольник.

Если в распоряжении ЛПР имеется m альтернатив, то этот

симплекс можно разбить на m непересекающихся подмножеств,

таких, что в любой точке этого подмножества оптимальной по

критерию Байеса является одна и та же альтернатива.

Такое подмножество (из

p ), соответствующее стратегии

x , называется байесовым множеством этой стратегии. Будем

обозначать его

()

px или

p .

Понятию байесова множества можно дать простую геомет-

рическую интерпретацию.

Если среда может находиться всего в двух состояниях n = 2

с вероятностями

1pp=−

, то симплекс

11 1

(0, 1)pp p≥≤

—

есть отрезок.

Математическое ожидание полезности при использовании

альтернативы

11 12 11 2 2

(, ) (1 ) ( )

ii iiii

Bpx p

yy y

=⋅+− = − +

Таким образом, каждой альтернативе

x соответствует пря-

мая на плоскости с системой координат (,)pB .

Приведем пример построения байесовых множеств

()

px в

одномерном симплексе при наличии трех альтернатив (рис. 5.2).

Множеству

()

соответствует отрезок симплекса, на котором

альтернатива

x обеспечивает максимум математического ожи-

дания полезности.

Можно доказать, что каждое байесово множество образует

(1)n − -мерном пространстве замкнутый выпуклый многогран-

ник (в нашем случае при n = 2 — отрезок, а при n = 3 — много-

гранник).

103

Объем этого многогранника будем рассматривать как меру

байесова множества

()

px и обозначим ее ()

. Назовем инте-

гральным потенциалом альтернативы

x величину

(, )

() ,

1()/( )

Bpx dp

−

π=

−µ µ

∫

где числитель характеризует интегральное (средневзвешенное

по всем априорным распределениям) байесово значение оце-

ночного функционала;

()

−

— мера (объем) симплекса, и, следовательно, зна-

менатель определяет геометрическую вероятность непопадания

вектора p в байесово множество альтернативы

x .

Естественно предположить, что ЛПР стремится к увеличе-

нию числителя при возможно меньшем знаменателе. Отсюда

получаем критерий наибольшего интегрального потенциала:

()max()

∗

π= π

)(

),(

xpB

max полезности на

множестве

)(

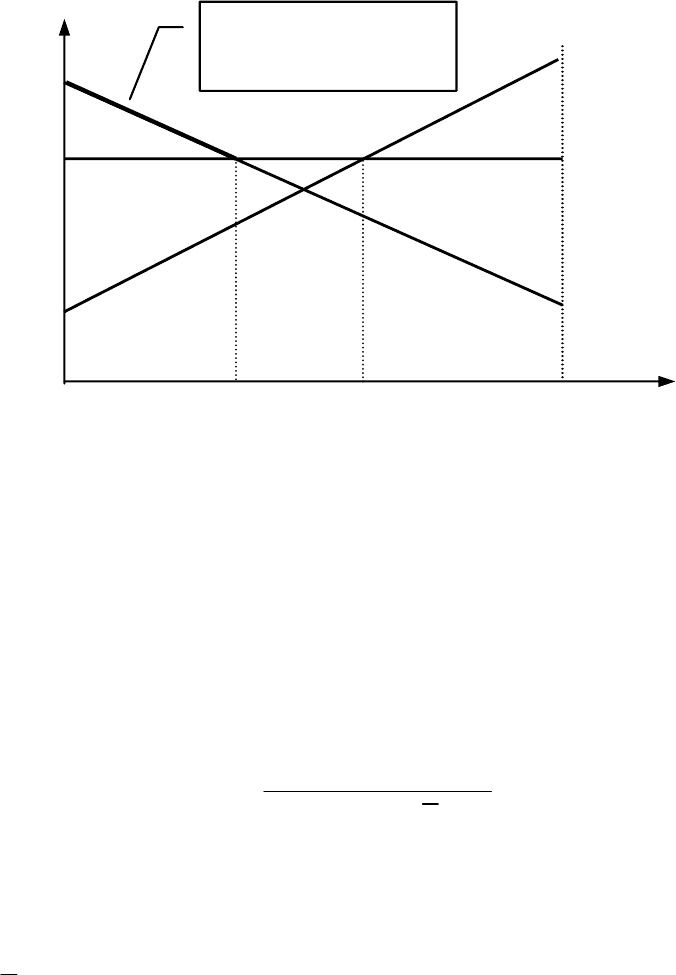
Рис. 5.2 — Пример построения байесовых множеств

)(

в одномерном симплексе при наличии трех альтернатив

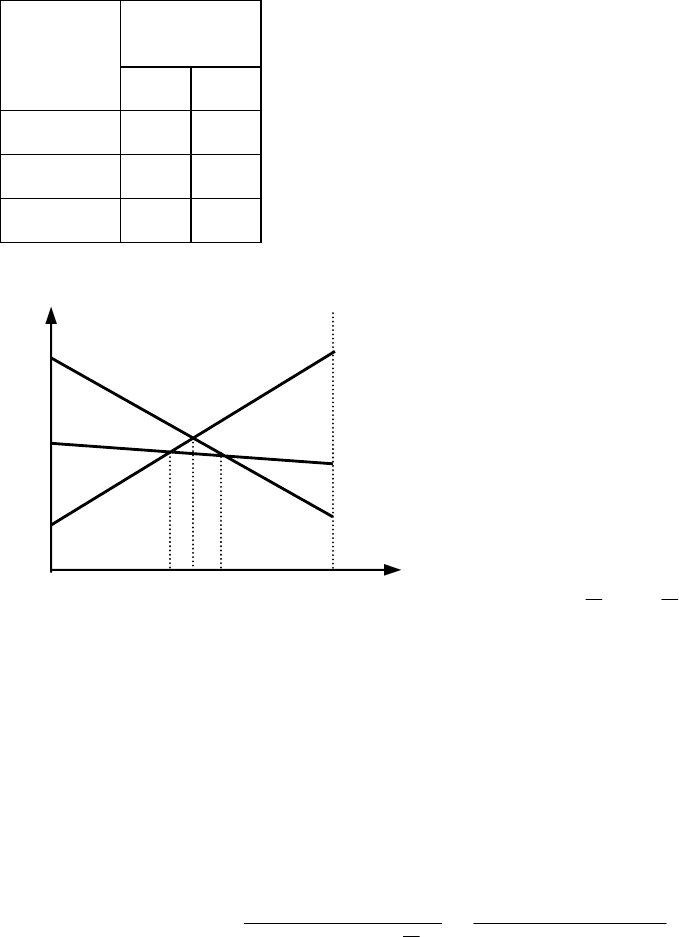
104

Пример

Задана матрица значений оценочного функционала (табл. 5.4).

Найдем зависимость

(,)

Bp x

математического ожидания по-

лезности от вероятности появления состояния

и изобразим ее

на рис. 5.3.

Таблица 5.4 —

Исходные данные

Стра-

тегия

2 11

6 7

11 3

Вычислим значения интегрального потенциала для всех

стратегий:

11 1

(, )

(11 9 )

() 8;

1()/() 1()

Bpx dp

pdp

pp p

−

π= = =

−µ µ −µ

∫

11 1 1 1

(,)2 11(1 )119Bp x p p p

+−=−;

12 1 13 1

(,)7 ; (,)38Bp x p Bp x p

−=+

()[0;0,47]; ( ) 0;

()[0,47;1]

px px

Длины соответствующих

отрезков:

53,047,01)(

;0)( ;47,0)(

=−=µ

=µ

Мера симплекса:

:( ) 1pp

= .

0,47

Рис. 5.3 — Иллюстрация

оценки альтернатив

0,44

0,5

105

0,47

(3 8 )

( ) 0. ( ) 7.

1()

pdp

π=π= =

−µ

∫

Оптимальной альтернативой следует считать

x .

5.3.3 Принятие решений в условиях противодействия

Имеется активная внешняя среда, которая стремится при-

нять такие состояния, сводящие к

минимуму эффективность

процесса управления. ПР в таких условиях рассматривается в

теории игр. Основными критериями ПР в этой ситуации явля-

ются:

1) максиминный критерий

Вальда, в соответствии с кото-

рым ЛПР выбирает такую стратегию, что при любом состоянии

внешней среды обеспечивается доход не меньше некоторой га-

рантированной величины (принцип наибольшего гарантирован-

ного результата):

( ) max min

Wx y

∗

;

2) критерий минимаксный

Сэвиджа, при использовании

которого минимизируются максимальные значения риска

или сожаления

( ) min max

Sx r

∗

()min max

Cx c

∗

Пример

Дана матрица доходов

(табл. 5.5).

Найдем в каждом столбце матрицы максимальный элемент:

max

jij

= ,

где

— доход, получаемый ЛПР, при условии, что оно знает

состояние внешней среды

106

Разность

()

jij

yβ−

между максимально возможным и ре-

альным доходом, соответствующим выбранной стратегии

x и

состоянию внешней среды

, называется риском

(табл. 5.6):

ij j ij

ry=β −

. Риск характеризует потери, которые несет ЛПР при

выборе альтернативы, отличной от оптимальной.

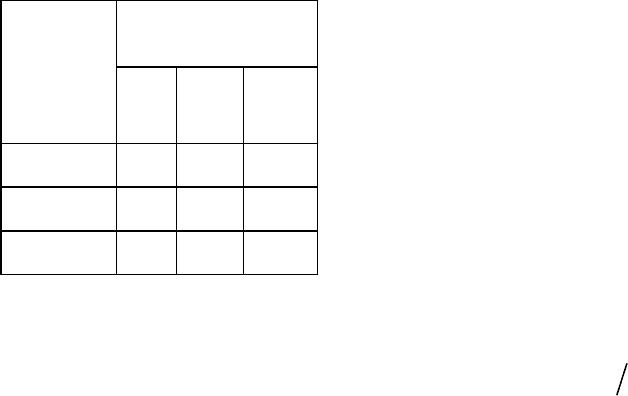
Таблица 5.5 —

Данные доходов

8 2 4

6 7 4

4 7 5

3 4 6

Таблица 5.6 —

Данные потерь

0 5 2

2 0 2

4 0 1

5 3 0

В некоторых ЗПР оценка исходов производится не по дохо-

ду, а по потерям

, которые несет ЛПР при альтернативе

x и

состоянии среды

Найдем минимальный элемент в каждом столбце

min

mU= , где

— минимальные потери ЛПР, при условии,

что оно знает состояние

. Сожаление — это разность:

2min

Альтернативы

x и

x дают наибольший га-

рантированный выигрыш.

Перейдем к матрице

риска

5max

Альтернатива

дает минимум потерь.

Эти потери дают абсо-

лютно надежную оценку

ПР в условиях физиче-

ской неопределенности.

107

ij ij j

CUm=−

. Оно определяет дополнительные (относительно

) потери ЛПР в случае неудачного для данного состояния

выбора альтернативы

x .

5.3.4 Принятие решений при наличии неопределенной

информации о состоянии внешней среды

ЛПР может установить некоторый уровень пессимизма-

оптимизма в отношениях наихудшего и наилучшего для него

состояний среды. Критерий

Гурвица учитывает в отличие от

критерия Вальда и Сэвиджа лишь частичный антагонизм внеш-

ней среды

(,) min (1 )max

iij ij

xy yϕλ=λ +−λ ,

где

— показатель Гурвица.

max ( , ) ( , ).

∗

λ=ϕ λ

При

1λ=

получаем критерий Вальда.

Пример

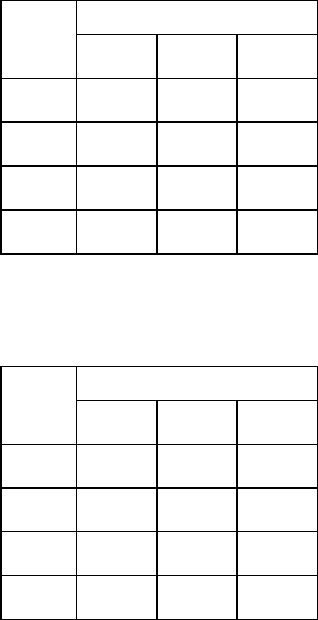
Дана матрица реализаций (табл. 5.7). При каких значениях

λ альтернативы будут наилучшими?

Таблица 5.7 —

Исходные данные

Стра-

тегии

Внешняя

Среда

2 10 7

6 7 7

11 8 3

xxf при всех

xxf , если 7811−λ + > − λ + или 47

≥ (рис. 5.4).

( , ) 2 (1 )10 8 10

(,) 6(1 )7 7

(,) 3(1 )11 8 11

ϕλ=λ⋅+−λ=−λ+

λ=λ⋅ + −λ =−λ+

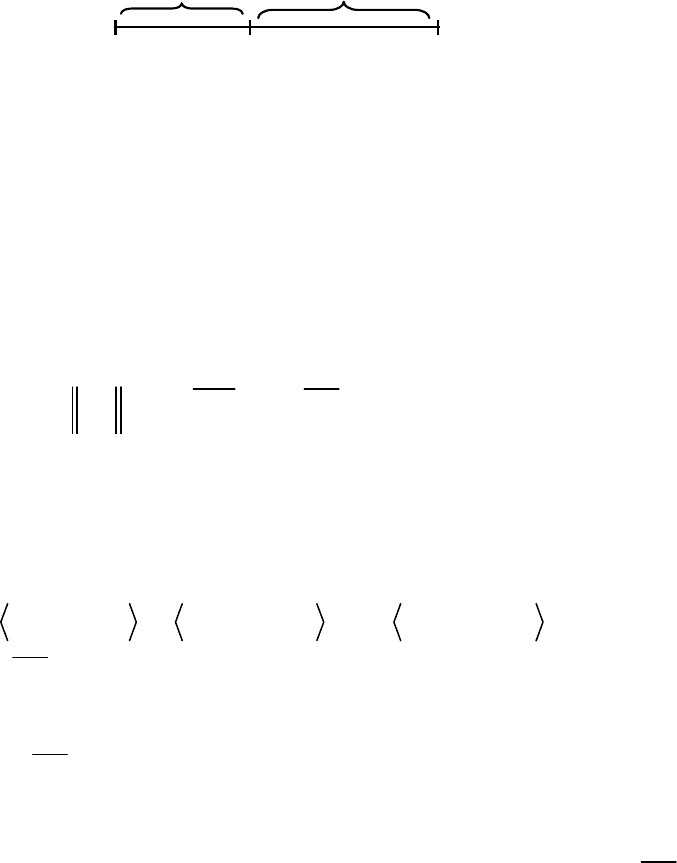
108

5.3.5 Принятие решений при нечетком описании

множества состояний внешней среды

ЛПР знает полный перечень состояний внешней среды

( , , ..., ),

Eee e= множество альтернатив

( , , ..., ),

xx x

матрицу исходов

, 1, ; 1, .

yimjn== Но имеющаяся инфор-

мация не позволяет четко определить состояние среды. Принятие

решения в таком случае осуществляется с использованием тео-

рии нечетких множеств [18, 38].

Пусть

( , , ..., )

Eee e= порождает нечеткое множество

{

}

11 1 2 2 2

( ) / , ( ) / , ..., ( ) / ,

nn n

Aeeee ee=µ µ µ

где

, 1,

eEj n∈=

— состояние среды, носитель нечеткого мно-

жества

;

(), 1,

ej nµ= — функция принадлежности состояния

нечеткому множеству

, ( ) [0,1].

∈

Полагаем, что функция принадлежности

(), 1,

ejnµ=

известна и множество ее значений для

∈

представлено век-

тором

( , ..., ).

µ= µ µ

Для оценки альтернатив могут быть использованы критерии

принятия решений в условиях вероятностной неопределенности

(п. 5.2.2), если вместо вероятности

использовать взвешен-

ную оценку, равную

µµ

∑

Например, при использовании

∗

4/7

Рис. 5.4 — Иллюстрация влияния

показателя Гурвица

109

критерия Байеса оценка альтернативы

будет иметь вид

(, ) .

ii ijj k

Bx y

µ= µ µ

∑∑

5.4 Принятие решений на основе нечеткого

отношения предпочтений

Рассмотрим следующую задачу. Пусть задано множество

альтернатив Х, каждая из которых характеризуется несколькими

признаками (критериями) с номерами

1, .jm= Информация о

парном сравнении альтернатив по каждому из признаков j пред-

ставлена в форме отношения предпочтения

R на множестве Х.

Задана относительная важность критериев

Задача заключается в том, чтобы по данной информации

сделать рациональный выбор альтернатив из множества

( , , ..., ).

Пример

В процессе разработки проекта возникла необходимость

привлечь дополнительных сотрудников для скорейшего выпол-

нения одного из этапов. У руководителя есть три возможности

преодолеть трудность:

1) обучить своего сотрудника;

2) найти и принять на работу сотрудника, умеющего вы-

полнять требуемые функции;

3) заключить договор с другой организацией о выполнении

этих работ.

Руководитель принимает решение, учитывая следующие

критерии:

1) быстроту выполнения работы;

2) материальные затраты на ее выполнение;

3) качество выполнения.

Будем считать, что все критерии одинаковы по важности.

Каждый критерий порождает отношения предпочтения на мно-

жестве альтернатив (возможностей) Х.

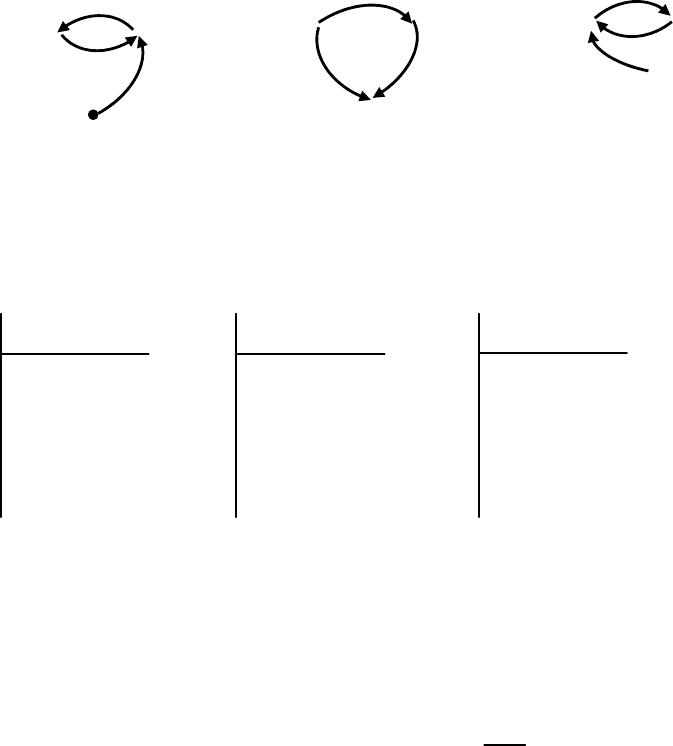
110

Пусть отношения предпочтения альтернатив по каждому

критерию будут представлены графами (рис. 5.5).

Отношения предпочтения альтернатив по трем критериям

будут заданы в виде следующих матриц:

110

011

321

xxx

100

110

111

321

xxx

101

011

321

xxx

В [18] предложен подход нахождения нечетного множества

недоминируемых альтернатив. Суть его заключается в том, что

вначале строятся нечеткие отношения предпочтения

Q и

Q на

множестве исходных альтернатив Х, такие, что функция

принадлежности нечеткого отношения

Q определяется через

пересечение исходных отношений

, 1, ,

Rj m=

а функция

принадлежности нечеткого отношения

Q определяется через

аддитивную свертку этих отношений. Затем через пересечение

нечетких множеств

определяется множество пред-

почтительных альтернатив с максимальной степенью недоми-

нируемости.

Определение

Пусть

— множество альтернатив,

— заданное на

нем нечеткое отношение предпочтения. Нечеткое подмножество

Рис. 5.5 — Графы отношений