Турунтаев Л.П. Теория принятия решений

Подождите немного. Документ загружается.

151

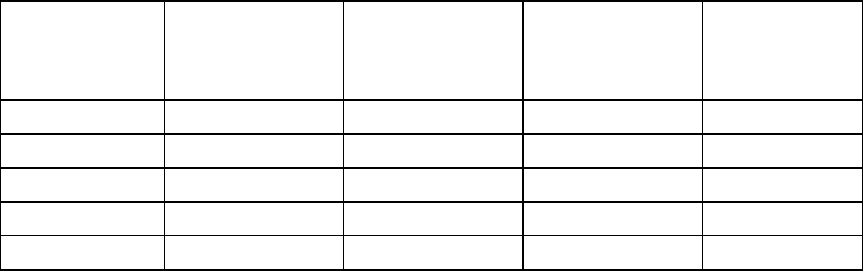
Стоимость

в $

Стоимость

нормиро-

ванная

Функция

полезности

Отноше-

ние

Жигули 4 000 0,24 0,2791 1,16

Москвич 3 000 0,18 0,2691 1,50

Иж 2 500 0,15 0,0858 0,57

Волга 7 000 0,43 0,3660 0,85

Сумма 16 000 1,00 1,00

Таким образом, учитывая предпочтения данного конкрет-

ного ЛПР, предлагаемая процедура рекомендует ему выбрать

Москвич.

Главным достоинством процедуры следует считать тот

факт, что веса критериев и оценки по субъективным критериям

не назначаются прямым волевым методом (как чаще всего пы-

таются делать, не сильно задумываясь о корректности такого

волюнтаризма), а определяются на основе метода парных срав-

нений. Другое достоинство — представление критериев в виде

иерархии (дерева). Такая структура внутренне присуща самому

понятию «критерий». Критерии по своей природе иерархичны и

они могут быть сопоставимы целям (дереву целей), отражая сте-

пень их достижения.

Основным недостатком процедуры следует признать вве-

дение понятия и установления «количественного превосходства

в N раз» сравниваемых объектов.

Контрольные вопросы

Назовите основные шаги процедуры STEM.

Какие принципы выбора компромиссных решений зало-

жены в процедуре STEM?

Назовите основные шаги метода «ЭЛЕКТРА».

Как определяются пороги согласия и несогласия?

Назовите основные шаги решения многокритериальной

задачи о назначениях.

Что такое дерево решений?

На решение каких задач ориентирован метод анализа ие-

рархий?

Опишите метод анализа иерархий.

152

7 ГРУППОВОЙ ВЫБОР И СИСТЕМЫ ПОДДЕРЖКИ

ПРИНЯТИЯ РЕШЕНИЙ

7.1 Групповые решения

7.1.1 Проблемы многокритериальных задач группового

выбора

До сих пор можно было считать, что у нас есть один экс-

перт или одно ЛПР. А что делать, если их несколько? Пусть, для

примера, мы готовим предложения для одного ЛПР и хотим

учесть мнение нескольких экспертов. Рассмотрим такой случай

применительно к модели критериального выбора.

При групповой экспертизе наиболее типична следующая

ситуация:

• у экспертов разные мнения по поводу набора критериев,

• у экспертов разные мнения о сравнительной значимости

критериев,

• эксперты дают разные оценки альтернатив по критериям.

Можно сказать, что методы группового выбора позволяют

структуризовать множество альтернатив в ситуации «разноголо-

сицы» суждений экспертов. Для начала вспомним, как преодо-

левается разница мнений в обычной практике. На ум тут же

приходит способ решения спорных вопросов методами голосо-

вания: консенсус (полное согласие), простое большинство, ква-

лифицированное большинство. При всей хрестоматийности и

широкой распространенности, эти методы имеют по меньшей

мере один существенный недостаток. Они отбрасывают мне-

ние меньшинства (кроме консенсуса, где изначальное меньшин-

ство попросту сводится на нет путем убеждения). В методах

поддержки принятия решений пытаются, по возможности, обра-

батывать экспертные суждения без отбрасывания. Действи-

тельно, ведь мы имеем дело с экспертами, т.е. со специалистами

высокой квалификации. Как же можно просто отбрасывать их

мнения? Иногда к отбрасыванию все же прибегают, но — в ред-

ких случаях, например в методах так называемой «борьбы с ма-

нипулированием», т.е. сознательным искажением экспертами

своих оценок с целью лоббирования тех или иных альтернатив.

153

Любители фигурного катания знают, что при выставлении оцен-

ки участнику соревнований крайние оценки судей отбрасывают-

ся, а оставшиеся усредняются. Это пример одного из простых

методов борьбы с манипулированием. Какие же методы приме-

няются для решения проблем, обозначенных в начале этого раз-

дела? При формировании набора критериев можно попросить

каждого эксперта дать свое множество критериев, а затем объе-

динить все множества в одно. Если есть жесткое ограничение по

количеству критериев, то тут без отбрасывания не обойтись.

Проще всего упорядочить критерии по частоте упоминания и

«подвести черту» в том месте, которое удовлетворяет заданному

ограничению.

Итак, набор критериев сформирован. Как получить их срав-

нительную значимость? Здесь хорош, например, метод построе-

ния компромиссной ранжировки [6]. Каждый эксперт дает свою

ранжировку критериев по важности. На основе индивидуальных

ранжировок нужно построить обобщенную. Это можно сделать

разными методами. Наиболее корректным (но и наиболее трудо-

емким) считается метод «медианы Кемени» (по имени автора —

американского математика и экономиста, лауреата Нобелевской

премии). Для нахождения медианы, прежде всего, нужно задать

способ определения расстояния между ранжировками, как гово-

рят математики, «определить метрику в пространстве ранжиро-

вок». После этого нужно найти (построить) такую ранжировку,

суммарное расстояние от которой до всех заданных экспертных

ранжировок было бы минимально. Искомая ранжировка и будет

медианой Кемени. Заметим, что тем самым мы получаем обоб-

щенное мнение экспертов, не отбрасывая ни одного мнения, по-

скольку при построении медианы существенно учитываются все

индивидуальные ранжировки.

Теперь займемся оценками альтернатив по критериям.

Итак, первое, что приходит в голову, — нужно взять среднее

арифметическое оценок экспертов. К сожалению, все не так

просто. Прежде всего, нужно задуматься о согласованности

экспертных суждений. Действительно, если эксперты оценива-

ют реальный объект, то их оценки не должны сильно расходить-

ся. А если они все-таки существенно расходятся? Тогда, прежде

всего, нельзя использовать среднее арифметическое, поскольку

154

тогда мы получаем так называемую «среднюю температуру по

больнице». Действительно, если сложить температуру всех вы-

сокотемпературных больных и температуру тел в морге, а потом

поделить на общее количество замеров, то можно получить 36,

°. Свидетельствует ли это о том, что «в среднем» все находя-

щиеся в больнице здоровы? Тем не менее абсурдность усредне-

ния оценок без предварительного анализа согласованности мало

кто понимает. А как считать согласованность? Если распределе-

ние оценок близко к Гауссовому, можно использовать стандарт-

ное отклонение. Если нет, нужно использовать непараметриче-

ские методы расчета согласованности. А если согласованность

все же оказалась низкой? В этом случае нужно пытаться выяс-

нить причину расхождений и, по возможности, попытаться уст-

ранить ее. Часто причиной может быть отсутствие важной ин-

формации у некоторых экспертов. Иногда ситуация слишком

неопределенна, «размыта». В некоторых случаях эксперты раз-

биваются на две устойчивые группы (ситуация разных научных

школ или ситуация «разработчики-эксплуатанты»). В этом слу-

чае также нельзя строить обобщенные оценки. Группы нужно

уметь выявлять и обрабатывать отдельно. Таким образом, спо-

соб обработки оценок в каждом конкретном случае должен под-

бираться индивидуально и тщательно обосновываться.

7.1.2 Постановка задачи группового выбора

Под групповым выбором понимается процедура принятия

коллективного решения на основе согласования индивидуаль-

ных предпочтений членов группы. Это согласование произво-

дится на основе принципа группового выбора, который опреде-

ляет правило согласования и выбора наилучшего решения.

Пусть для решения проблемной ситуации предложен ряд

вариантов решений

( , ..., ).

xx= Имеется групповое ЛПР,

состоящее из

коалиций (малых групп) — объединений участ-

ников группового выбора с совпадающими целями. Каждый

член

коалиции

j может выбирать решения в соответствии со

своими предпочтениями

,1,, 1,.

iljs==

155

Оценка решений коалицией

представляет собой вектор

индивидуальных предпочтений

( , ..., )

jlj

. Для образо-

вания единого группового предпочтения

(, ..., )

FF F

необ-

ходимо согласовать индивидуальные предпочтения

в коа-

лициях (раздел 7.1.3), а затем — коалиционные решения в виде

единого решения по некоторым принципам группового выбора

(раздел 7.1.4). Рассмотрим наиболее распространенные принци-

пы коллективного выбора [6, 12, 43].

7.1.3 Принятие коллективных решений в малых

группах

Имеется групповое ЛПР, состоящее всего из одной коали-

ции, отражающей общность целей всех ее членов. Необходимо

согласовать индивидуальные предпочтения членов группы по

соответствующим принципам и выбрать наилучшее решение.

Принцип большинства голосов утверждает, что групповое

предпочтение должно соответствовать предпочтению коалиции,

которая имеет число голосов, превышающих некоторый порог.

Если порог равен половине участников группового ЛПР (51 %),

то говорят о принципе простого большинства голосов, при по-

роге в ¾ голосов — о принципе подавляющего большинства го-

лосов, при пороге, близком к 100 %, — о принципе абсолютного

большинства, при пороге в 100 % — о принципе единогласия

(консенсуса).

Как отмечается в [3], правило большинства привлекательно

своей простотой и экономичностью, но имеет некоторые осо-

бенности:

• только дальнейшая практика показывает, правильным

или ошибочным было решение, принятое большинством голо-

сов (само голосование — лишь форма согласования дальнейших

действий);

• даже в простейшем случае выбора одной из двух альтер-

натив легко представить себе ситуацию, когда правило боль-

шинства не срабатывает — разделение голосов поровну при

четном числе голосующих.

156

В соответствии с принципом диктатора в качестве груп-

пового предпочтения принимается предпочтение одного лица

группы (коалиции). Ввиду того, что при данном принципе со-

вершенно не учитываются предпочтения других членов группы,

понятие группового ЛПР теряет содержательный смысл. Прин-

цип диктатора характерен для военных организаций и широко

используется при принятии решений в чрезвычайных обстоя-

тельствах.

Принцип диктатора и большинства голосов не учитывает

интересы всех членов группы. Их применение в принципе при

отсутствии определенных сдерживающих факторов может при-

вести к распаду группового ЛПР.

Французский ученый маркиз де Кондорсе (1743–1794 гг.)

сформулировал принцип или критерий, позволяющий опреде-

лить победителя в демократических выборах.

Принцип де Кон-

дорсе

состоит в следующем [12]: кандидат, который побежда-

ет при сравнении один на один с любым из других кандидатов,

является победителем на выборах.

Каждый из голосующих упорядочивает кандидатов по сте-

пени своего желания видеть его победителем. Согласно де Кон-

дорсе, справедливое определение победителя возможно путем

попарного сравнения кандидатов по числу голосов, поданных

из-за них. Однако вскоре маркиз де Кондорсе столкнулся с па-

радоксом, получившим впоследствии его имя.

Согласно

методу Борда результаты голосования выража-

ются в виде числа баллов, набранных каждым из кандидатов

[12]. Если число кандидатов равно n, то за первое место прису-

ждается n баллов, за второе —

)1(

−

n балл, за последнее — один

балл.

Рассмотрим примеры голосования в собрании представите-

лей из 60 человек [12].

Пример 1. Парадокс де Кондорсе

Пусть на голосование поставлены три кандидата: CBA ,, и

голоса распределились, как в таблице 7.1.

157

Таблица 7.1 — Примеры распределения голосов

Число голосующих

№

пп

Предпочтения

Пример 1 Пример 2 Пример 3

CBA →→

23 0 0

BCA →→

0 23 31

ACB →→

17 19 12

CAB →→

2 0 0

BAC →→

10 2 2

ABC →→

8 16 15

Сравним предпочтения по отношению к парам кандидатов.

Берем

и B : тогда

предпочитают 331023)( =+→ BAB ;

предпочитают .278217)(

→ ABA Следовательно,

предпочтительнее

)( BAB

→

по воле большинства. Аналогично

сравним другие пары (табл. 7.2).

Таблица 7.2 — Попарное распределение голосов

B C

– 23+10=33 23+2=25

17+2+8=27

– 23+17+2=42

17+10+8=35 10+8=18 –

Анализируя распределение голосов, приходим к противоре-

чию, к

нетранзитивному отношению ACBA →→→ .

Столкнувшись с этим парадоксом (нетранзитивным отно-

шением), де Кондорсе выбрал решение, которое поддерживается

большинством голосов:

CBA →→

(23+0 >17+2 > 10+8). При-

чина данного парадокса нетранзитивности группового выбора в

цикличности совокупности исходных индивидуальных предпоч-

тений.

Пример 2. Принцип большинства

Пусть голоса по трем кандидатам распределились иначе

(табл. 7.1). Нетрудно подсчитать, что при этих новых результа-

тах голосования, в соответствии с принципом Кондорсе, попар-

158

ное распределение голосов будет представлено таблицей 7.3, а,

в соответствии с принципом Кондорсе, избранным будет канди-

дат

, который при попарном сравнении побеждает двух дру-

гих кандидатов (

AC → с числом голосов, равным 37, и BC →

с числом голосов, равным 41). В целом отношение между тремя

кандидатами по принципу Кондорсе будет

ABC →→

. Однако

если применить принцип большинства голосов, то отношение

между тремя кандидатами будет

CBA →→

(23 > 19 > 18) и

победителем оказывается кандидат

. Но при этом кандидат

не набрал простого большинства голосов (51 %).

Таблица 7.3 — Попарное

распределение голосов

B C

— 25 23

— 19

37 41 —

Пример 3. Метод Борда.

Применим метод Борда к приведенному выше примеру 2. Для

каждого кандидата баллы распределятся следующим образом:

.13831632219223:

,11421612319123:

,10811622119323:

=⋅+⋅+⋅+⋅

⋅

+⋅+⋅+⋅

В соответствии с методом Борда следует объявить победи-

телем кандидата

C , как и по принципу Кондорсе. Однако с ме-

тодом Борда тоже возникают проблемы. Рассмотрим результаты

голосования для примера 3 (табл. 7.1). Подсчитав баллы для ка-

ждого кандидата методом Борда, получим:

A( — 124, B — 99,

— 137 ) . Следовательно в соответствии с методом Борда по-

бедителем следует считать кандидата

C . Однако по принципу

большинства голосов следует считать победителем кандидата

(31 голос из 60).

Приведенные примеры (табл. 7.4) позволяют считать, что

парадоксы при голосовании не возникают лишь в случае, когда

159

победитель определяется по принципу большинства голосов при

пороге 51 %.

Однако такой случай нетипичен для большинства выборов,

поэтому прибегают к проведению двух туров голосования. Во

второй тур выходят два кандидата, набравшие большинство го-

лосов. Но и при такой системе сохраняются парадоксы голосо-

вания [3, 12, 43].

Таблица 7.4 — Результаты голосования

Варианты голосования

Правила

голосования

Пример 1 Пример 2 Пример 3

Кондорсе нетранзитив-

ность

Большинство голосов

(38,3 %)

(51,1 %)

Борда

B C C

7.1.4 Коалиционный выбор

Имеется групповое ЛПР, состоящее из нескольких коали-

ций со своими функциями предпочтений. Следует согласовать

коалиционные решения по некоторым принципам группового

выбора, обеспечивающим в некотором смысле выбор «опти-

мальных» решений и устойчивость существования всей группы.

Принцип оптимальности Курно отражает индивидуаль-

ную рациональность: ни одному участнику/коалиции группово-

го ЛПР отдельно невыгодно менять своего решения за неимени-

ем лучшего.

По принципу Парето группа может улучшать свои реше-

ния без несения ущерба каждому участнику. Этот принцип при-

меним при сильной зависимости всех участников группового

ЛПР.

Конкретизация принципов согласования группового выбора

может быть приведена в следующих условиях отношений между

коалициями: статус-кво, конфронтации, рациональности [6, 43].

При отношении статус-кво коалиции стараются сохранить

существующее положение. При отношении конфронтации коа-

лиции действуют так, чтобы навредить друг другу. При отноше-

160

нии рациональности коалиции действуют в собственных инте-

ресах, что, естественно, не обязательно приносит ущерб другим

коалициям.

Рассмотрим применение

принципов группового выбора

в условиях гипотезы статус-

кво на примере [6]. Пусть име-

ется групповое ЛПР, вклю-

чающее всего два члена.

Сформулировано два варианта

решения проблемы, и каждый

из членов группы в соответст-

вии со своими предпочтения-

ми

может выбрать любое

решение (в табл. 7.5 даны ранговые оценки).

Поэтому возможны следующие варианты решений при

групповом выборе:

11 12

(, )

— первый член группы выбрал решение

x , вто-

рой член группы — решение

x ;

11 22

(, )

— первый член группы выбрал решение

, вто-

рой член группы — решение

x ;

21 12

(, )yy — первый член группы выбрал решение

x , вто-

рой член группы — решение

;

21 22

(, )

— первый член группы выбрал решение

x , вто-

рой член группы — решение

x .

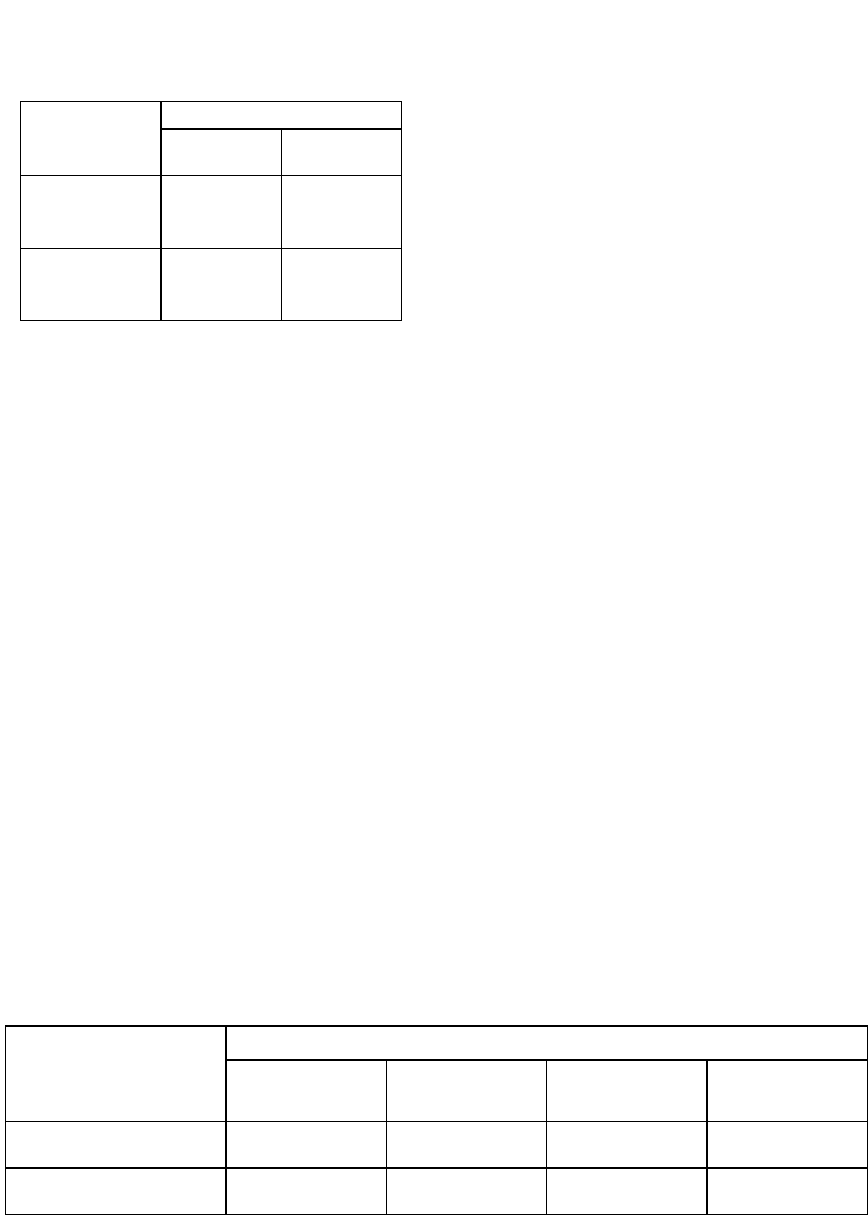
Допустим, что члены группового ЛПР высказали свои

предпочтения состояний в рангах (табл. 7.6).

Таблица 7.6 — Групповое предпочтение

Решения

Предпочтение

состояний

),(

1211

),(

2211

yy ),(

1221

),(

2221

1 3 3 2

2 3 3 1

Таблица 7.5 — Индивидуальные

предпочтения

Члены группы

Решение

x 1

=y 2