Удут Л.С., Кояин Н.В., Мальцева О.П. Проектирование и исследование автоматизированных электроприводов. Часть 1. Введение в технику регулирования линейных систем Часть 2. Оптимизация контура регулирования
Подождите немного. Документ загружается.

действительной положительной осью –
)(
. Кривую, которую
описывает конец этого вектора при изменении частоты от 0 до
,
называют амплитудно-фазовой частотной характеристикой (АФЧХ).
Модуль
)()( jWA
называют амплитудной частотной
функцией, а ее график – амплитудной частотной характеристикой (АЧХ).
Модуль
)(A
представляет собой коэффициент усиления системы на
конкретной частоте
гармонического входного сигнала, т. е.
m
m
x
y
A )(
, где
m
y
и
m
x
– амплитуды, соответственно, выходного и входного
сигналов на частоте
.
Аргумент или фазу
)(arg)( jW
называют фазовой частотной
функцией, а ее график – фазовой частотной характеристикой (ФЧХ).
Фаза
( )
представляет собой угол сдвига выходного сигнала
относительно гармонического входного сигнала на частоте
.
Вещественную часть
)( Re)( jWP
и мнимую часть
)( Im)( jWQ
называют, соответственно, вещественной и мнимой
частотной функцией, а их графики – вещественной и мнимой
частотной характеристикой.
Если на вход линейной системы поступает периодическое
воздействие в виде суммы бесконечно большого числа гармоник
1
1
sin)(
k
k
tkxtx
, (1.19)
то в соответствии с принципом суперпозиции, справедливым для
линейной системы, вынужденное установившееся движение системы
представляет собой сумму этих же гармоник с изменившейся в
)(
1
jkW
раз амплитудой и фазовым сдвигом
)(
1
k
1
11
)(sin)()(
k
k
kkjWxty
, (1.20)
где угловая частота
имеет дискретное значение
1
k
,
const
1
.
Таким образом, при гармоническом воздействии в устойчивых
системах после окончания переходного процесса выходная координата
также изменяется по гармоническому закону, но с амплитудой,
отличной от заданной, и фазовым сдвигом, не равным нулю. При этом
отношение амплитуд выходной и входной величин равно модулю, а
сдвиг фазы – аргументу частотной передаточной функции.
Следовательно, АЧХ показывает изменение отношения амплитуд, а
ФЧХ – сдвиг фазы выходной величины относительно входной в
зависимости от частоты входного гармонического воздействия.
Частотные методы нашли широкое применение для синтеза и
анализа (в том числе и экспериментальным путем) систем
регулирования. Это объясняется четкой зависимостью между
параметрами временных и частотных характеристик разомкнутой и
11

замкнутой систем регулирования. Для косвенной оценки устойчивости
систем регулирования разработаны частотные критерии
устойчивости Михайлова и Найквиста. Критерий Михайлова
рассматривает частотный годограф
)( jA
замкнутой системы, который
получается из собственного оператора A(p) или характеристического
многочлена системы
)(A
заменой
jp
или
j
. Частотный
критерий Найквиста позволяет судить об устойчивости замкнутой
системы регулирования по виду амплитудно-фазовой характеристики
)( jW
разомкнутой системы. Вместо амплитудно-фазовой частотной
характеристики можно построить отдельно: амплитудную частотную
характеристику
)( jW
и фазовую частотную характеристику
( )
;
вещественную частотную характеристику
)(P
и мнимую частотную
характеристику
)(Q
. График функции
)( jW
строится чаще всего в
логарифмическом масштабе
)(lg20)( jWL
и называется
логарифмической амплитудной частотной характеристикой (ЛАЧХ).
График функции
( )
строится в полулогарифмическом масштабе (в
функции
lg
) и называется логарифмической фазовой частотной
характеристикой (ЛФЧХ).
Передаточные функции разомкнутого, а иногда и замкнутого
контура можно представить в виде произведения передаточных
функций (последовательного включения) элементарных (или типовых)
звеньев (см. подраздел 1.2)
n
i
i
pWpW
1
)()(
.
Тогда модули и аргументы частотных передаточных функций
системы
)()( jWA
и
)(arg)( jW
и звеньев
)()( jWA
ii
и
)(arg)( jW
ii
, в соответствии с правилом модулей и аргументов
комплексных чисел, связаны между собой соотношениями
n
i
i
AA
1
)()(
; (1.21)
n
i
i
1
)()(
. (1.22)
Выражение (1.21) в логарифмическом масштабе принимает вид
n
i
i
LL
1
)()(
. (1.23)
Проектирование по типовым частотным характеристикам (обычно
логарифмическим) отдельных контуров широко применяется в практике
систем автоматизированного электропривода. Общий характер связи
частотных и временных характеристик контура регулирования может
быть выражен следующим образом: сжатой вдоль оси времени t
временной характеристики y(t) соответствует растянутая вдоль оси
12

соответствующая ей частотная характеристика
)( jW
замкнутого
контура и наоборот. Другими словами, чем шире полоса пропускания
контура, тем выше его быстродействие.
Хотя преобразование Фурье и предполагает нахождение
временной функции y(t) как решения уравнения (1.1), сделать это не
проще, чем непосредственно решить исходное дифференциальное
уравнение. Переходный процесс может быть построен приближенным
графоаналитическим методом трапеций по вещественной частотной
характеристике
)(P
. Но для получения сравнительно простого и
экономичного решения линейных дифференциальных уравнений
пользуются операционным исчислением. Чаще всего используется
преобразование Лапласа:
• прямое преобразование
0
de)()( ttxsF
st
; (1.24)
• обратное преобразование
jc
jc
st
ssF
j
tx de)(
2
1
)(
, (1.25)
где в общем случае
jcs
, но для большинства функций времени,
рассматриваемых в системах регулирования, с = 0 и тогда
js
.
Выражения (1.24) и (1.25) справедливы при нулевых начальных
условиях, т. е. если при
0t
x(t)=0 и все ее производные равны нулю,
управляющие и возмущающие воздействия равны нулю.
Преобразовав дифференциальное уравнение (1.3) по Лапласу при
нулевых начальных условиях, получим алгебраическое уравнение
относительно изображений
)()()()()()( sZsDsXsBsYsA
, (1.26)
где
01
)( asasasA
n
n
;
01
)( bsbsbsB
m
m
;
01
)( dsdsdsD
k
k
;
Y(s), X(s), Z(s) – изображения по Лапласу временных функций
(оригиналов) y(t), x(t), z(t);
)(
)(
)(
)(
)(
у
sA
sB
sX
sY
sW
и
)(
)(
)(
)(
)(
в
sA
sD
sZ
sY
sW
(1.27)
– передаточные функции или передаточные функции в форме
преобразований Лапласа системы по управлению и возмущению –
отношение изображения по Лапласу выходной величины системы к
изображению входной величины при нулевых начальных условиях.
Определение передаточной функции (1.27) не находится в
противоречии с определением согласно (1.5), так как при нулевых
начальных условиях комплексная переменная s может быть
13

отождествлена с оператором дифференцирования p и переход от одной
формы записи передаточной функции к другой производится простой
заменой p на s и наоборот.
Используя передаточную функцию (1.27), систему регулирования,
описываемую дифференциальным уравнением (1.3), можно представить
(при z = 0) в виде структурной схемы (рис. 1.6). Передаточная функция
)(
у
sW
характеризует систему в области изображений по Лапласу.
Рис. 1.6. Структурная схема,
составленная относительно
изображений переменных
Если в выражениях (1.27) принять
js
, то получим частотные
передаточные функции по управлению и возмущению вида (1.17), а
если в полиноме A(s) принять
s
, то получим характеристическое
уравнение вида (1.11).
Основное достоинство преобразования Лапласа заключается в
том, что в результате переходят от дифференциального уравнения к
алгебраическому и операции дифференцирования и интегрирования
оригинала (функции времени) заменяются алгебраическими действиями
(умножением и делением) по отношению к изображениям. Решая
алгебраическое уравнение, находят изображение решения
дифференциального уравнения. Переход от изображения решения к
самому решению может быть произведен по выражению (1.25) или
таблицам. В результате с помощью преобразования Лапласа можно
сравнительно просто производить решение линейных
дифференциальных уравнений с постоянными коэффициентами.
Поэтому операционное исчисление целесообразно применять для
анализа переходных и установившихся процессов в автоматических
системах управления. Однако возможность и доступность современной
вычислительной техники позволяет эти же задачи более эффективно
решать с использованием численных методов решения
дифференциальных уравнений и методов имитационного
моделирования систем практически любой сложности. Эти методы, в
отличие от операционного исчисления, хорошо вписываются в общую
процедуру машинных методов синтеза и анализа систем
автоматического регулирования.
Заключение по разделу. Выше были введены понятия трех
передаточных функций для систем автоматического регулирования:
операторная W(p), частотная
)( jW
и в форме изображения Лапласа
W(s). Передаточную функцию W(p) следует рассматривать не более как
некоторый оператор, осуществляющий преобразование входной
14
)(
)(
)(
у
sA
sB
sW
)(
sX
)(
sY

величины x(t) в выходную y(t) в соответствии с дифференциальным
уравнением. Передаточная функция W(s) – это обычная алгебраическая
функция комплексного переменного s, а
)( jW
– комплексная функция
от действительной переменной
, и с ними можно производить
соответствующие математические операции. Для линейных систем
регулирования с постоянными параметрами, которые соответственно
описываются линейными дифференциальными уравнениями с
постоянными коэффициентами, названные передаточные функции с
точностью до обозначений совпадают и находятся путем простой
замены p = s или
jp
, или
js
. Также дополнительно введена
комплексная величина
для записи характеристического уравнения,
которое получается путем замены
p
в операторе A(p) или
s
в
полиноме A(s). Авторы ставили своей целью обратить внимание на
имеющие место различия в понятиях, символах и переменных и дать
основу для осмысленной работы с литературными источниками по
теории и системам автоматического управления, где нет такого
дифференцированного подхода. Для более глубокого освоения теории
линейных систем автоматического управления рекомендуется
обратиться к литературным источникам [2, 3] из приведенного к
разделу списка литературы.
Список литературы к подразделу 1.1
1. Д. Сю, А. Мейер. Современная теория автоматического
управления и ее применение: пер. с англ. / под ред. Ю.И. Топчеева. –
М.: Машиностроение, 1972. – 544 с.
2. Иванов В.Н. и др. Математические основы теории
автоматического регулирования: учеб. пособие для вузов / под ред. Б.К.
Чемоданова. – М.: Высшая школа, 1971. – 808 с. (гл. 5,6,12,15).
3. Бабаков Н.А., Воронов А.А и др. Теория автоматического
управления: учеб. для вузов. Ч. 1. Теория линейных систем
автоматического управления / под ред. А.А. Воронова. – М.: Высшая
школа, 1986. –367 с.
4. Иващенко Н.Н. Автоматическое регулирование. Теория и
элементы систем: учебник для вузов. – М.: Машиностроение, 1978. –
736 с. (гл. 10–13).
5. Топчеев Ю.И. Атлас для проектирования систем
автоматического регулирования: учеб. пособие для вузов. – М.:
Машиностроение, 1989. – 752 с. ( гл. 1 и 4).
6. Бесекерский В.А., Попов Е.П. Теория систем
автоматического регулирования. – М.: Наука, 1978. – 736 с. (гл. 11).
15
7. Макаров И.М., Менский Б.М. Линейные автоматические
системы (элементы теории, методы расчета и справочный материал):
учеб. пособие для вузов. – М.: Машиностроение, 1977. – 464 с. (гл. 2–6).
1.2. Типовые динамические звенья линейных систем регулирования
1.2.1. Классификация звеньев
Элементы систем регулирования, различные по физической
природе, но описываемые линейными дифференциальными
уравнениями одного и того же вида, являются одинаковыми
динамическими звеньями. В теории автоматического регулирования
принята классификация звеньев в зависимости от вида их передаточных
функций, т. е. в конечном итоге в зависимости от вида
дифференциального уравнения, описывающего поведение звена. У
каждого динамического звена может быть лишь одна входная и одна
выходная величина. Элементы с несколькими входными или
выходными величинами разделяют на соответствующее число
динамических звеньев.
Числитель и знаменатель в выражении (1.5) представляют собой
многочлены с действительными коэффициентами, разложив которые на
простые сомножители, передаточную функцию в общем случае можно
записать в виде
r
l
ll
q
q
n
i
m
j
jjji
pTpTpTp
pTpTpTk
pW
1
2
2
1
1 1
22
121
121
)(
, (1.28)
где
, , r
– количество действительных, комплексных сопряженных и
нулевых корней многочлена А(p);
n, m – количество действительных и комплексных сопряженных
корней многочлена B(p) или D(p).
В передаточную функцию (1.28) входят шесть различных видов
сомножителей:
,
12
1
;
1+
1
;
1
;12 1;+ ;
22
22
TppT
Tpp
TppTTpk
(1.29)
где k – передаточный коэффициент;
T – постоянная времени;
– относительный коэффициент затухания (демпфирования);
t
p
d
d
– оператор дифференцирования.
16

Таким образом, отдельный элемент системы регулирования и саму
систему в целом можно рассматривать в общем случае как
последовательное соединение простейших структурных звеньев,
называемых типовыми. В соответствии с видом сомножителей (1.29) в
табл. 1.1 приведены типовые динамические звенья и представлено их
деление по основным свойствам на четыре группы: пропорциональные
(безынерционные), инерционные, интегрирующие и
дифференцирующие.
Пропорциональные и инерционные звенья, кроме
консервативного, характеризуются тем, что в каждом из них при подаче
на вход постоянной величины с течением времени устанавливается
постоянное значение выходной величины. Другими словами, при
подстановке p = 0 в передаточную функцию этих звеньев, получается
выражение статической характеристики
xky
, где
constx
. Для
остальных типовых звеньев невозможно описать статическую
характеристику: возникающие в консервативном звене колебания
никогда не затухают; выходная величина интегрирующего звена при
постоянном входном воздействии неограниченно растет
)(
стат
k
;
дифференцирующее звено реагирует лишь на изменения входной
величины
)0(
стат
k
.
При практической реализации интегрирующего звена может иметь
место вносимый схемой дополнительный эффект замедления или
форсирования (см. п. 8, 9 и 11.2 табл. 1.1). Реализация же идеальных
дифференцирующих звеньев вообще практически оказывается
невозможна и тогда специально используют эффект замедления перед
дифференцированием (см. п. 10 и 11.1 табл. 1.1).
На структурных схемах звенья изображаются прямоугольником
(рис. 1.7). Входящая в него стрелка обозначает входную величину,
направленная от него – выходную. Поведение выходной величины в
зависимости от входной может быть охарактеризовано для статического
(установившегося) состояния или при изменении во времени.
Если координатные оси расположены посредине прямоугольника,
то нанесенная на них характеристика относится к статическому режиму
(рис. 1.7, а). По оси абсцисс откладывается входная величина, по оси
ординат – выходная. Для обозначения динамических свойств звена в
прямоугольнике изображается переходная функция в стилизованной
форме или записывается передаточная функция звена (рис. 1.7, б и 1.7, в).
Элементы (устройства) систем регулирования на электрических схемах
могут иметь условные одно- или двухбуквенные обозначения
(буквенный код), например AI, где первая буква означает его вид –
устройство (регулятор), а вторая – его функцию (интегрирующее) [5].
17
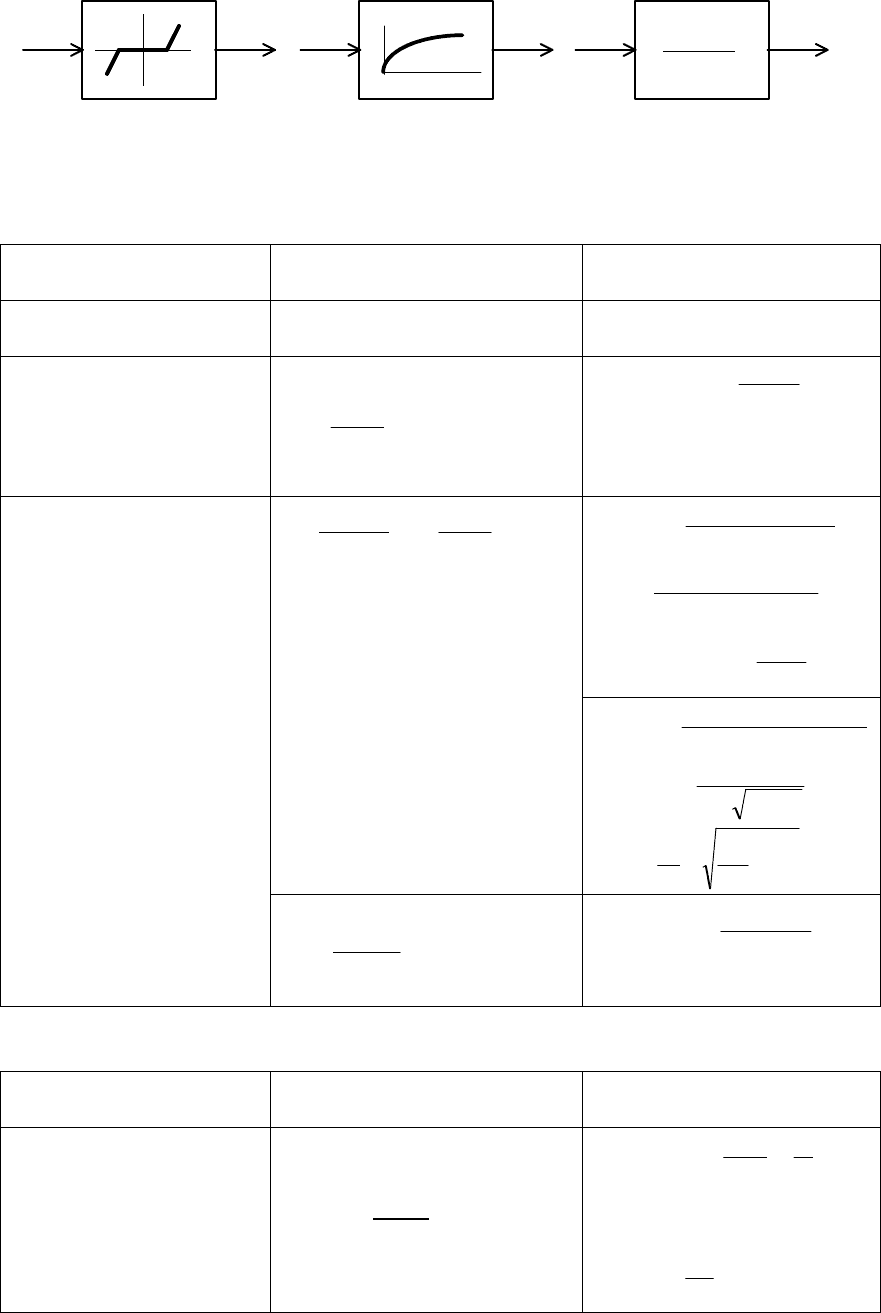
k
Tp 1
x(t) y(t)y(t)yx x(t)
а б в
Рис. 1.7. Условные обозначения звеньев
Таблица 1.1
Типовые динамические звенья
Тип звена
Дифференциальное
уравнение
Передаточная функция
(в операторной форме)
1. Пропорциональное
(безынерционное)
)()( txkty
kpW )(
2. Инерционное
(апериодическое) 1-
го порядка
)()(
d
)(d
txkty
t
ty
T
1
)(
Tp
k
pW
,
где Т – инерционная
постоянная
времени
3. Инерционное 2-го
порядка
)(
)(
)(d
)(d
d
)(d
1
2
2
2
2
txk
ty
t
ty
T
t
ty
T
,
12
1
)(
22
2
1
22
2
TppT
k
pTpT
k
pW
где
2
1
2
2
;
T
T
TT
3.1. Колебательное
10;2
21
TT
3.2. Апериодическое
2-го порядка
(последовательное
включение двух
апериодических звеньев)
43
21
;1;2
TT
TT
,
)1)(1(
)(
43
pTpT
k
pW
где
1
2
4,3
T
T
или
2
2
2
11
4,3
42
T
TT
T
3.3. Консервативное
(вырожденное
колебательное при
0
)
)()(
d
)(d
2
2
2
2
txkty
t
ty
T
,
1
)(
22
pT
k
pW
где
2
TT
Продолжение табл. 1.1
Тип звена
Дифференциальное
уравнение
Передаточная функция
(в операторной форме)
4. Интегрирующее
идеальное
)(
)(d
)(d
tx
t
ty
T
p
k
pT
pW
и
1
)(
,
где
TT
и
– постоянная
интегрирования;
и
1
T
k
18
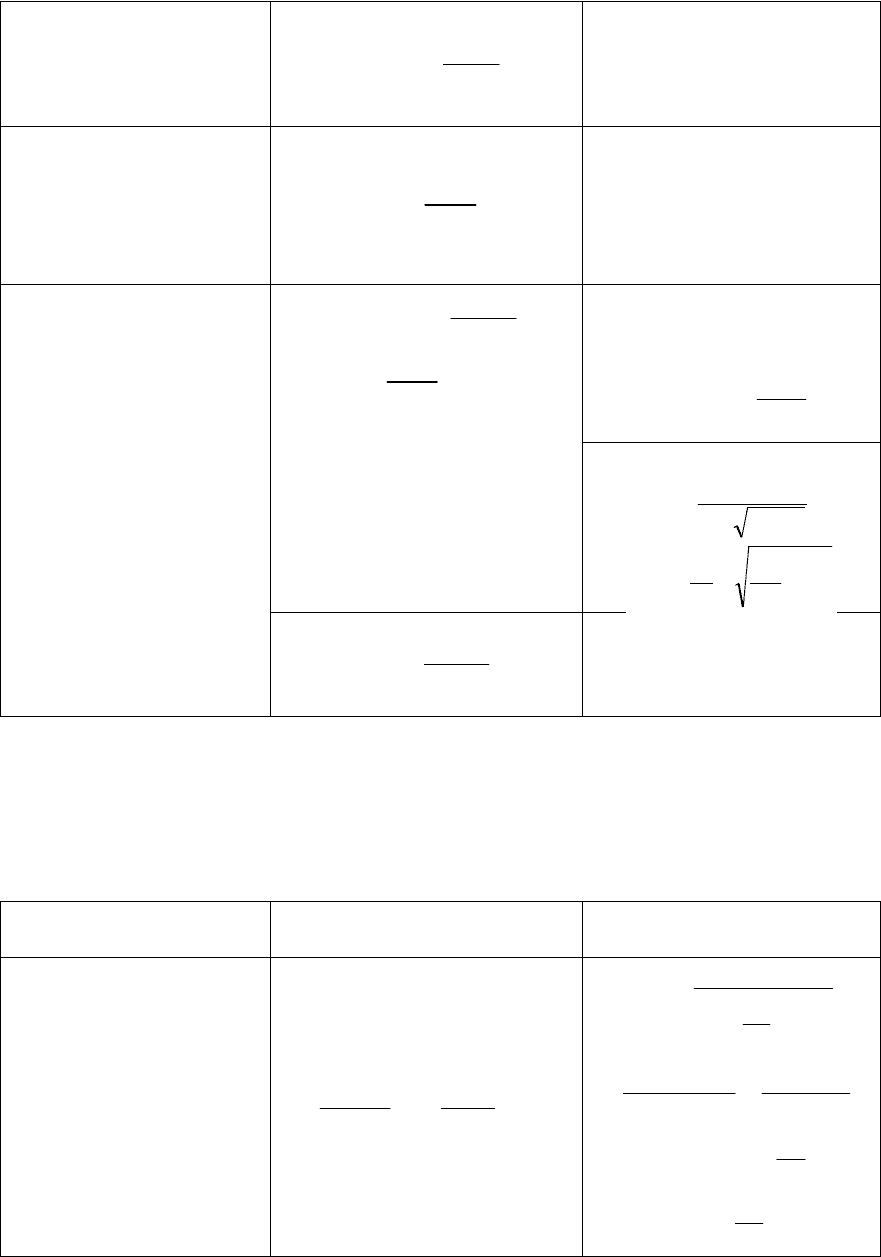
5. Дифференцирующее
идеальное
t
tx
Tty
d
)(d
)(
kppTpW
д
)(
,
где
TT
д
– постоянная
дифференцирования;
д
Тk
6. Дифференцирующее
идеальное 1-го
порядка
)(
d
)(d
)( tx
t
tx
Tkty
,
)1()(
д
уп
kpT
pTkpW
где
TT
уп
– постоянная
упреждения;
TkТ
д
7. Дифференцирующее
идеальное 2-го
порядка
)(
)(d
d
)(d
)(
1
2
2
2
2
tx
dt
tx
T
t
tx
Tkty
10;2
21
TT
,12
1)(
2
1
2
2
TppTk
pTpTkpW
где
2
1
2
2
;
T
T
TT
7.1. Последовательное
включение двух
дифференцирующих
звеньев 1-го порядка
4321
;1;2 TTTT
,1
1)(
4
3
pT
pTpW
где
;
1
2
4,3
T
T
2
2
2
11
4,3
42
T
TT
T
7.2. Вырожденное
дифференцирующее
2-го порядка (
0
)
)(
d
)(d
)(
2
2
2
2
tx
t
tx
Tkty
,
1)(
22
22
2
kpkT
pTkpW
где
2
TT
Окончание табл. 1.1
Тип звена
Дифференциальное
уравнение
Передаточная функция
(в операторной форме)
8. Реальное
(инерционное или с
замедлением)
интегрирующее
)(
)(d
)(d
d
)(d
1
2
2
2
tx
t
ty
T
t
ty
T
,
Tpp
k
TppT
p
T
T
pT
)p(W
11
1
1
1
и
1
2
1
где
;;
1
2
1и
T
T
TTT
и
1
T
k
19

9. Изодромное
(форсирующее
интегрирующее) 1-го
порядка
*
)(
)(d
)(d
d
)(d
12
tx
t
tx
T
t
ty
T
,
1
1
1
1
)(
ии
из
2
1
pT
k
pT
pT
pT
pT
pW
где
1из
TT
– постоянная
изодрома;
2и
2
1
; TT
T
T
k
10. Реальное
(инерционное или с
замедлением)
дифференцирующее
12
12
)(d
)(d
)(
d
)(d
TT
t
tx
Tty
t
ty
T
11
)(
д
2
1
Tp
pT
pT
pT
pW
,
где
21д
; TTTT
11.
Интегродифференци
рующее звено
первого порядка
)(
)(d
)(d
)(
d
)(d
1
2
tx
t
tx
Tk
ty
t
ty
T
1
1
)(
2
1
pT
pT
kpW
11.1. Реальное
(инерционное или с
замедлением)
дифференцирующее
1-го порядка
21
TT
11.2. Пассивное
интегрирующее
звено
21
TT
Примечание. Для типовых звеньев общепринято k = 1; неединичный
коэффициент передачи здесь и далее принят с целью иллюстрации общего
случая. * Изодромное звено (ПИ-регулятор) будет рассмотрено в
подразделе 1.5.
1.2.2. Пропорциональное (безынерционное) звено
Между входной и выходной величинами пропорционального
звена отсутствует сдвиг во времени: выходная величина мгновенно
повторяет в k раз измененном масштабе входное воздействие в
независимости от его вида.
Дифференциальное уравнение и передаточная функция звена
приведены в табл. 1 (п. 1). Переходная функция звена при единичном
входном воздействии x(t) = 1(t) имеет вид
kth )(
, (1.30)
и тогда при ступенчатом входном воздействии
0
)( xtx
(см. выражение
(1.12) в подразделе 1.1) переходный процесс для выходной координаты
находится по выражению
20
