Ван Хорн Д., Вахович Д. Основы финансового менеджмента

Подождите немного. Документ загружается.

Глава 3. Стоимость денег во времени 121

Неизвестная процентная (или дисконтная) ставка. Преобразовав базовое

уравнение для будущей (приведенной) стоимости аннуитета, можно решить

его относительно процентной (или дисконтной) ставки, используемой при на-

числении сложных процентов, если нам известны: 1) будущая (приведенная)

стоимость аннуитета, 2) размер периодической выплаты или получения и 3)

применяемое количество периодов. Допустим, что через семь лет вам потребу-

ется по меньшей мере 9500 долл., чтобы отправить своих родителей в захваты-

вающий круиз. Чтобы накопить эту сумму, вы решаете помещать в конце каж-

дого года 1000 долл. на сберегательный счет в банке. Какую минимальную

процентную ставку должен обеспечивать этот банк (при условии ежегодного

начисления сложных процентов), чтобы осуществился ваш план накопления

сбережений?

Чтобы вычислить процентную ставку (г), удовлетворяющую условиям на-

шей задачи, воспользуемся уравнением (3.9) для будущей стоимости аннуитета:

FVA

=R(FVIFA

)

$9500 = $1000(*УЖ4,

)

МД

=$9500/$1000 = 9,5.

Просматривая в табл. 3.5 строку, соответствующую восьмилетнему периоду,

находим коэффициент будущей стоимости аннуитета (FVIFA), ближайший к вы-

численному нами значению, — 9,5. Ближайшим к числу 9,5 значением коэффици-

ента будущей стоимости аннуитета является 9,549, которое мы находим в столбце,

соответствующем 5%. Поскольку 9,549 несколько больше, чем 9,5, мы приходим

к выводу, что процентная ставка в рассматриваемой ситуации на самом деле

должна быть несколько меньше 5%. (Чтобы получить более точный ответ, придет-

ся воспользоваться либо методом проб и ошибок, проверяя разные процентные

ставки, либо методом интерполяции, либо финансовым калькулятором.)

Неизвестное количество периодов начисления сложных процентов (или

дисконтирования). Работая с аннуитетами, нередко приходится сталкиваться

с ситуациями, когда известны будущая (приведенная) стоимость аннуитета,

процентная ставка и количество периодических выплат (или поступлений)

денег. При этом требуется определить сумму каждой равной выплаты (или

поступления). В бизнес-целях чаще всего приходится определять периодиче-

ские выплаты по аннуитету применительно к задачам, связанным с фондом

погашения (sinking fund) (т.е. созданием определенного денежного фонда пу-

тем взноса равных сумм) и амортизацией займа (loan amotization) (т.е. пога-

шением займа путем выплаты равных сумм).

Чтобы определить величину периодических выплат или получения денег,

предусмотренных аннуитетом, необходимо преобразовать базовое уравнение

для приведенной (будущей) стоимости аннуитета. Поскольку важному вопросу

амортизации займов посвящен специальный раздел в конце этой главы, мы по-

кажем, как вычислить величину периодических выплат применительно к задаче

определения фонда погашения.

Какую сумму нужно депонировать в конце каждого года на сберегательный

счет, чтобы по истечении восьми лет накопить 10 тыс. долл., если на депозит на-

числяется доход по 5%-ной ставке? Сумму (К), которую необходимо депониро-

122 Часть II. Оценка активов

вать на сберегательный счет в конце каждого года, можно вычислить с помощью

уравнения (3.9) для будущей стоимости аннуитета. Кроме того, для нахождения

стоимости, соответствующей FVIFA

5%S

, мы воспользуемся табл. 3.5. В результате

получаем:

FVA

= R(FVIFA

)

$10000 = ^(9,549)

R = $10 000/9,549 = $1047,23.

Таким образом, депонируя в конце каждого года 1047,23 долл., мы получим

на сберегательном счете по истечении восьми лет искомую сумму — 10 тыс.

долл. (при использовании 5%-ной ставки для начисления сложных процентов).

Срочный аннуитет. В отличие от обычного аннуитета, при котором вы-

платы или денежные поступления происходят в конце каждого периода, сроч-

ный аннуитет (annuity due) предусматривает последовательность выплат или

денежных поступлений, происходящих в начале каждого периода. К счастью,

решение задач, касающихся срочного аннуитета, требует лишь минимальной

модификации уже описанных нами процедур решения задач, касающихся

обычного аннуитета.

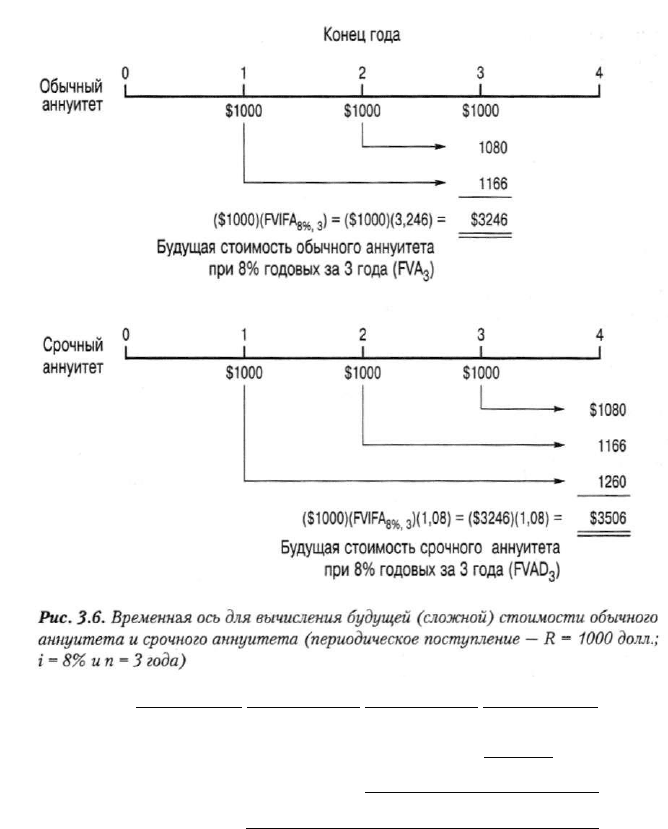
На рис. 3.6 сравниваются процедуры вычисления будущей стоимости

обычного аннуитета величиной 1000 долл., выплачиваемого в течение трех лет

при 8% годовых (FVA

), и будущей стоимости срочного аннуитета величиной

1000 долл., выплачиваемого в течение трех лет при 8% годовых (FVAD^). Обра-

тите внимание: создается впечатление, что денежные потоки для обычного

аннуитета возникают в конце периодов 1, 2 и 3, а денежные потоки для срочно-

го аннуитета возникают в начале периодов 2, 3 и 4.

Следует также обратить внимание на то, что будущая стоимость трехлет-

него срочного аннуитета равняется будущей стоимости сопоставимого трех-

летнего обычного аннуитета, с начисленным одним дополнительным перио-

дом. Таким образом, будущая стоимость срочного аннуитета при i процентах

для п периодов (FVADJ равняется

FVAD

R(FVIFA

)(l

+ i). (3.14)

Ответ на вопрос о том, появляется ли денежный поток в конце или в начале

периода, зачастую зависит от точки зрения наблюдателя, (Вопрос о том, яв-

ляется ли полночь концом одного дня или началом следующего, относится

к той же категории.) Таким образом, истинным критерием, который позволяет

различать будущую стоимость обычного аннуитета и срочного аннуитета, яв-

ляется момент, по отношению к которому вычисляется эта будущая стои-

мость, Для обычного аннуитета его будущая стоимость вычисляется как бу-

дущая стоимость всех платежей на момент поступления последнего из них.

Для срочного же аннуитета момент расчета его будущей стоимости сдвига-

ется еще на один период после завершающего платежа.

Глава 3. Стоимость денег во времени 123

Срочный • ] \ \ j

аннуитет $

1СЮ

о $юоо $1000

*•

$1080

1166

1260

($1000)(FVIFA

8%i3

)(1,08) = ($3246)(1,08) = $3506

Будущая стоимость срочного аннуитета

при 8%

годовых

за 3

года

(FVAD

)

Рис. 3.6. Временная ось для вычисления будущей (сложной) стоимости обычного

аннуитета и срочного аннуитета (периодическое поступление — R = 1000 долл.;

i = 8% ип= 3 года)

Определение приведенной стоимости срочного аннуитета при i процентах

для п периодов (PVAD

) проще всего уяснить на конкретном примере. Рис. 3.7

иллюстрирует вычисления, связанные с определением как приведенной стои-

мости обычного аннуитета (1000 долл.) при 8% годовых за три года (PVA

), так

и приведенной стоимости срочного аннуитета (1000 долл.) при 8% годовых за

три года (PVAD

Как видно из рис. 3.7, приведенная стоимость трехлетнего срочного аннуи-

тета равняется приведенной стоимости двухлетнего обычного аннуитета

плюс одно недисконтированное периодическое поступление или выплата де-

нег. Этот вывод можно обобщить в следующем виде:

PVAD

= RiPVIFA,^ ) + R =

= R(PVIFA

+ l). (3.15)

И наоборот, приведенную стоимость срочного аннуитета можно рассматривать

как приведенную стоимость обычного аннуитета, отнесенного на один период

в прошлое. Иными словами, нам требуется приведенная стоимость на один период

позже, чем необходимо для вычисления стоимости обычного аннуитета. Таким

образом, мы могли бы вычислить приведенную стоимость аннуитета за п перио-

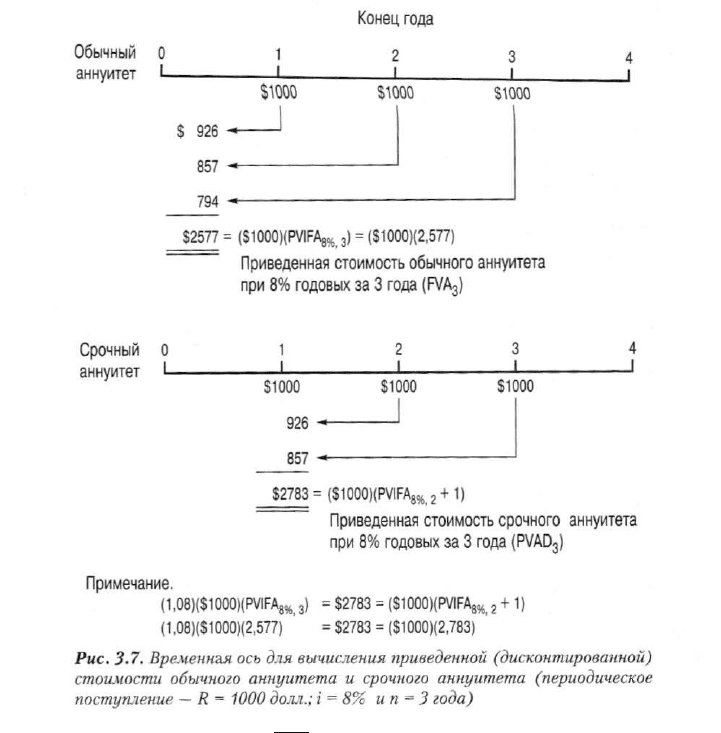
124 Часть II. Оценка активов

дов, а затем начислить ее на один период "вперед". Универсальная формула для

такого подхода к определению PVADn имеет следующий вид:

PVAD

=(i + i)(R)(PVIFA

). (3.16)

$2783 = ($1000)(PVIFA

8%2

+1)

Приведенная стоимость срочного аннуитета

при 8% годовых за 3 года (PVAD

)

Примечание.

(1,08)($1000)(PVIFA

/O] 3

) = $2783 = ($1000)(FWA

8%| 2

+ 1)

(1,08)($Ю00)(2,577) ' = $2783 = ($1000)(2,783) '

Рис. 3.7. Временная ось для вычисления приведенной (дисконтированной)

стоимости обычного аннуитета и срочного аннуитета (периодическое

поступление — R = 1000 долл.; г = 8% ип= 3 года)

Рис. 3.7 свидетельствует о том, что оба подхода к определению PVAD

одина-

ково хороши. Однако использование уравнения (3.15) представляется более оче-

видным. Подход, основанный на использовании временной оси (см. рис. 3.7), так-

же помогает нам уяснить разницу между значениями приведенной стоимости

обычного и срочного аннуитета.

Решая задачи, касающиеся определения приведенной стоимости обычно-

го аннуитета, мы считаем, что денежные потоки имеют место в конце вре-

менных периодов (в примере, показанном на рис. 3.7, — окончания перио-

дов 1, 2 и 3), и вычисляем приведенную стоимость аннуитета на момент вре-

мени, отстоящий на один период от первого денежного потока.

Определение приведенной стоимости срочного аннуитета предполагает

возникновение денежных потоков в начале временных периодов (в нашем

примере это соответствует началу периодов 1, 2 и 3) и вычисление приве-

денной стоимости аннуитета на момент первого платежа.

Глава 3. Стоимость денег во времени 125

Смешанные денежные потоки

Очень часто бывает, что в задачах, связанных с определением временной

ценности денег, отсутствует как единственный денежный поток, так и единст-

венный аннуитет. Вместо этого нередко приходится иметь дело со смешанной

(или неравномерной) картиной денежных потоков.

ВОПРОС

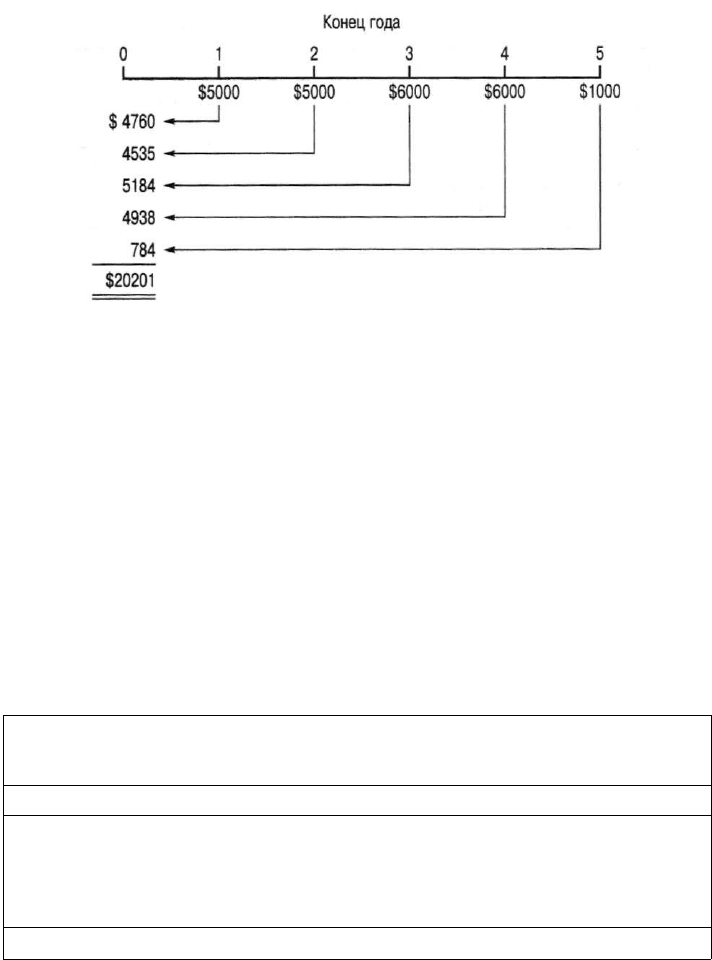
Допустим, что вам необходимо решить следующую задачу— возможно,

на экзамене. Какова общая приведенная стоимость следующих поступ-

лений: 5000 долл., которые мы должны получать ежегодно (в конце 1-го

и 2-го года), затем — 6000 долл. (получаемых нами в конце 3-го и 4-го года)

и заканчивая последней выплатой нам 1000 долл. в конце 5-го года (все

поступления дисконтируются по 5%-ной ставке)?

Первый шаг в получении ответа на поставленный выше вопрос (и решении

любой другой подобной задачи) заключается в том, чтобы начертить времен-

ную ось (временной график), разместить на ней денежные потоки, начертив

стрелки, указывающие их направление (денежные поступления или выплаты)

и позицию, по отношению к которой вы производите расчеты (так называемая

"позиция настройки"). Затем необходимо выполнить вычисления в соответст-

вии с построенным вами графиком. (Построение графика, отражающего необ-

ходимую последовательность действий, кое-кому может показаться "детской

забавой". Советуем, однако, вспомнить, что строительство любого дома начи-

нается с чертежей. А мы чем хуже?)

Рис. 3.8 показывает, что задачи о смешанных потоках всегда можно решить

путем индивидуальной "настройки" каждого потока на временном графике и

последующего суммирования результатов. Такой подход требует немало вре-

мени, но он обязательно окупит себя.

Зачастую в смешанных денежных потоках удается распознать определен-

ную закономерность, что дает возможность несколько упростить вычисления.

Таким образом, задача, которую мы пытаемся решить, имеет несколько аль-

тернативных вариантов решения. Одна из таких альтернатив показана на

рис. 3.9. Обратите внимание на то, как наша двухшаговая процедура посте-

пенно подводит нас к правильному решению.

Шаг 1. Начертить ось времени, позиционировать денежные потоки и начер-

тить стрелки, указывающие направление и позицию настройки.

Шаг 2. Выполнить вычисления, предусматриваемые построенным вами

графиком.

Мы могли бы привести множество примеров задач, касающихся смешан-

ных (ИЛИ неоднородных) денежных потоков. Чтобы оценить все разнообразие

таких задач и освоить приемы, необходимые для их решения, настоятельно

рекомендуем решить задачи, приведенные в конце этой главы. Не переживай-

те, если поначалу вы будете допускать какие-то ошибки. Задачи, касающиеся

изменения стоимости денег во времени, бывают достаточно сложными. Ос-

воение этого материала похоже на процесс обучения езде на велосипеде. Ов-

126 Часть II. Оценка активов

ладение необходимыми навыками и в том, и в другом случае связано с неиз-

бежными падениями, шишками и ссадинами (в первом случае о падениях,

шишках и ссадинах мы говорим, разумеется, в переносном смысле). Но это,

пожалуй, единственный способ чему-то научиться.

= FV

(PVIF

i) =

$5000(0,952)

$ 4760

= FV

(PVIF

0] 2

) =

$5000(0,907)

4535

PVfj = FV

(PVIF

0] 3

) = $6000(0,864) = 5184

PVrj = FV

<PVIF

/o> 4

) = $6000(0,823) = 4938

PVfj = FV

(PVIF

0] 5

) = $1000(0,784) = 784

Приведенная стоимость смешанных 201

денежных потоков при 5% годовых за 5 лет ==

Рис. 3.8. (Вариант 1) Временная ось для вычисления приведенной (дисконти-

рованной) стоимости смешанных денежных потоков (FV, = FV

= 5000 долл.;

= FV

= 6000долл.;FV

= 1000долл.;i = 5% ип= 5лет)

Волшебная процентная ставка для начисления сложных процентов

Каждый год в свой день рождения вы помещаете очередные 2000 ДОЛЛ. на свой пен-

сионный инвестиционный счет, не облагаемый налогом. По достижении 65-летнего

возраста вы накопите*:

Годовая процентная став-

ка для начисления слож-

ных процентов

Начальный возраст (лет)

(%)

21 (долл.) 31 (долл.) 41 (долл.) 51 (долл.)

425 487

222 870 109 730

46 552

773 011

344 634 146212

54 304

437 810

542 048 196694

63 544

31 41 51

2 716460 863 326

266 668 74 560

* Проанализировав таблицу, можно прийти к выводу, что лучше всего приступать к накопле-

нию сбережений прямо сейчас]

Глава 3. Стоимость денег во времени

127

Начисление сложных процентов

несколько раз в течение года

Полугодичный и другие периоды начисления

сложных процентов

Будущая стоимость. До сих пор мы предполагали, что проценты выпла-

чиваются ежегодно. Такое предположение существенно облегчает понимание

основ изменения стоимости денег во времени. Сейчас, однако, наступило вре-

мя рассмотреть взаимосвязь между будущей стоимостью и процентными

ставками для различных периодов начисления процентов. Предположим, что

128 Часть II. Оценка активов

проценты по вкладу выплачиваются раз в полгода. В этом случае, если вы по-

мещаете 100 долл. на сберегательный счет при номинальной (nominal) (или

объявленной (stated)) годовой процентной ставке, равной 8%, будущая стои-

мость по истечении шести месяцев составит:

$100(1+[0,08/2])

= $104.

Иными словами, в конце полугодия вам должны начислить 4%, а не 8%. В кон-

це года будущая стоимость вашего вклада составит:

Щ =$100(1 + [0,08/2])

=$108,16 .

Эта сумма равнялась бы 108 долл., если бы процент выплачивался лишь

раз в год. Разница в 0,16 долл. объясняется тем, что проценты за вторые шесть

месяцев начисляются на дополнительные 4 долл., начисленные в конце пер-

вых шести месяцев. Чем большее число раз на протяжении года начисляются

проценты, тем большей оказывается будущая стоимость в конце данного года.

Номинальная (объявленная) процентная ставка (nominal (stated) interest rate)

Процентная ставка, указываемая применительно к периоду в один год и не коррек-

тируемая в соответствии с частотой начисления процентов. Если проценты начис-

ляются несколько раз в год, эффективная процентная ставка оказывается выше, чем

номинальная процентная ставка.

Универсальная формула для определения будущей стоимости по истече-

нии п лет, когда процент начисляется m раз на протяжении одного года, имеет

следующий вид:

=PV

(l + [i/m]r • (3-17)

Чтобы проиллюстрировать использование этой формулы, допустим, что

новые проценты выплачиваются поквартально. Допустим также, что вы хоти-

те знать будущую стоимость 100 долл. в конце одного года, когда объявленная

годовая ставка равняется 8%. В этом случае будущая стоимость равняется:

Щ= $100(1 + [0,08/4])

<4)<1)

= $100(1 + 0,02)

=$108,24,

что, конечно же, больше, чем мы получили бы при использовании полугодич-

ного или ежегодного начисления сложных процентов.

Будущая стоимость по истечении трех лет в случае поквартального начис-

ления сложных процентов составит:

= $100(1+ [0,08/4])

(4)<3)

= $100(1 + 0,02)

=$126,82,

а в случае полугодичного начисления сложных процентов:

= $100(1 + [0,08/ 2] )

(2)(3)

= $100(1 + 0,04)

=$126,53.

Глава 3. Стоимость денег во времени 129

В случае ежегодного начисления сложных процентов будущая стоимость

по истечении трех лет составит:

= $100(1 + [0,08/1])

(1)(3)

= $100(1 +0,08)

=$125,97.

Таким образом, чем чаще в течение года выплачивается процент, тем боль-

шей оказывается будущая стоимость. Когда т в уравнении (3.17) стремится к

бесконечности, мы приближаемся к непрерывному начислению (continuous

compounding) процентов. Вскоре мы более подробно остановимся на непре-

рывном начислении и дисконтировании.

Приведенная стоимость. Когда проценты начисляются чаще, чем один

раз в год, формулу для вычисления приведенной стоимости необходимо пере-

смотреть в том же плане, что и формулу для вычисления будущей стоимости.

Вместо того чтобы делить будущий денежный поток на (1+г)", как мы посту-

паем в случае ежегодного начисления сложных процентов, приведенная стои-

мость определяется с помощью формулы

=FVJ(l+[i/m]r, (3.18)

где, как и раньше, FV

представляет собой будущий денежный поток, который

будет получен по окончании года п, т— сколько раз за год начисляются слож-

ные проценты, a i — ставка дисконтирования. Воспользовавшись уравнением

(3.18), мы могли бы вычислить, например, приведенную стоимость 100 долл.,

полученных по истечении трех лет, при начисляемой поквартально 8%-ной но-

минальной ставке дисконтирования:

=$100/(1 + [0,08/4])

(4)(3>

= $ 100/(1 + 0.02)

=$78,85.

Если ставка дисконтирования начисляется лишь раз в год, мы получим:

=$100/(1 + 0,08)

=$79,38 .

Таким образом, чем меньшее количество раз в год происходит начисление

номинальной ставки дисконтирования, тем большей оказывается приведенная

стоимость. Эта взаимосвязь является полной противоположностью тому, что

мы наблюдаем в случае будущей стоимости.

Непрерывное начисление сложных процентов

Иногда проценты начисляются непрерывно. Таким образом, небесполезно

было бы рассмотреть, как это происходит на практике. Вспомним, что общая

формула (3.17) для вычисления будущей стоимости по истечении п лет имеет

следующий вид:

=PV

(l+[i/m]r.

Когда т (частота начисления процентов на протяжении одного года) стре-

мится к бесконечности (°°), мы получаем ситуацию непрерывного начисления

130 Часть II. Оценка активов

процентов, а член (1+[г/т])тп стремится к ein, где е приблизительно равняет-

ся 2,71828. Следовательно, будущая стоимость первоначального депозита РУ

по истечении п лет — при условии непрерывного начисления процентов

(процентная ставка равняется г) — составит:

=PV

(e)

. (3.19)

Вернемся к нашему примеру. Будущая стоимость вклада в 100 долл. по ис-

течении трех лет в случае непрерывного начисления процентов (процентная

ставка равняется 8%) составит:

=$100(e)

08K3)

= $100(2,71828)

((Ш)

=$127,12,

Сравним полученное нами значение с величиной будущей стоимости в слу-

чае ежегодного начисления процентов:

= $100(1 + 0,08)

= $125,97.

Непрерывное начисление сложных процентов позволяет получить макси-

мально возможную будущую стоимость по истечении п периодов при задан-

ной номинальной процентной ставке.

Используя тот же ход рассуждений, приходим к выводу, что в случае не-

прерывного начисления процентов формула для приведенной стоимости де-

нежного потока, получаемого по истечении п лет, примет следующий вид:

=FV

/(ey

. (3.20)

Таким образом, приведенная стоимость 1000 долл., которые мы получим по

истечении 10 лет при начисляемой непрерывно 20%-ной ставке дисконтиро-

вания, составляет:

РУ

=$1000/(е)

20)(10>

= $1000/(2,71828)

=$135,34.

Из полученных нами результатов можно сделать вывод о том, что вычисление

приведенной стоимости в связи с непрерывным начислением процентов представ-

ляет собой процесс, обратный вычислению будущей стоимости. Следует также

отметить, что в то время как непрерывное начисление процентов позволяет полу-

чить максимально возможную будущую стоимость, оно же приводит к минималь-

но возможной приведенной стоимости.

ВОПРОС — ОТВЕТ

Объясните ситуацию, когда банк предлагает клиентам привлечь их сред-

ства на сберегательный вклад или приобрести депозитный сертификат

на условиях начисления годовой процентной доходности ?

Основываясь на одном из законов, принятых Конгрессом США, Федеральная

резервная система (ФРС) США требует, чтобы банки и прочие ссудосбере-

гательные учреждения использовали стандартный метод вычисления эффек-