Ван Хорн Д., Вахович Д. Основы финансового менеджмента

Подождите немного. Документ загружается.

Глава 14. Риск и управленческие опционы.

621

ЕСЛИ инвесторы (акционеры) и кредиторы не склонны к риску (а весь

имеющийся у нас практический опыт говорит именно в пользу такого предпо-

ложения), руководство фирмы должно включить показатель риска рассматри-

ваемого инвестиционного проекта в свой анализ его привлекательности. В про-

тивном случае решения, касающиеся планирования долгосрочных инвестиций,

вряд ли будут соответствовать целям максимизации стоимости акций фирмы.

После того как мы выявили необходимость учета риска, связанного с инвести-

циями, нам предстоит решить задачу измерения риска для конкретных инвести-

ционных предложений. Однако не следует забывать, что риск, связанный с той

или иной последовательностью денежных потоков, может изменяться (и зачас-

тую действительно изменяется) в будущем, в течение которого имеют место эти

потоки. Иными словами, распределения вероятностей вовсе не обязательно ос-

таются неизменными в разные периоды времени.

Год

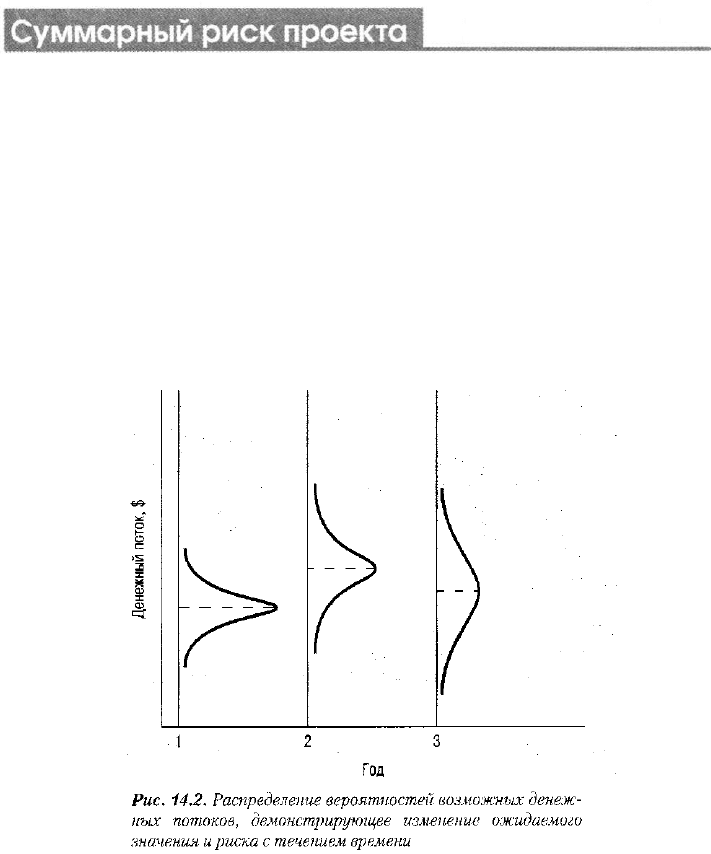
Рис. 14.2. Распределение вероятностей возможных денеж-

ных потоков, демонстрирующее изменение ожидаемого

значения и риска с течением времени

Это положение проиллюстрировано на рис. 14.2 для гипотетического инве-

стиционного проекта. Распределения напоминают приведенные на рис. 14.1,

правда, на этот раз они не дискретны, а непрерывны. Это означает, что величи-

на денежного потока для каждого периода может принимать любое значение

в некотором заданном интервале, а не строго определенные. Таким образом,

каждый график на рис. 14.2 представляет собой непрерывную линию, а не ряд

полосок, подобных тем, которые показаны на рис. 14.1. Как и раньше, чем

"компактнее" и "острее" распределение, тем меньше риск. Ожидаемое значе-

ние каждого из показанных на рис. 14.2 распределений представлено горизон-

тальной пунктирной линией. Мы видим, что и ожидаемое значение денежного

потока, и дисперсия распределения вероятностей с течением времени изме-

622 Часть V. Инвестиции в основной капитал

няются. Мы должны хорошо уяснить действие этого фактора, что даст нам

возможность выполнить количественную оценку степени риска рассматри-

ваемого инвестиционного предложения.

Подход, основанный на использовании дерева

вероятностей

Дерево вероятностей (probability tree)

Графический или табличный подход к организации возможных последовательностей

денежных потоков, генерируемых инвестиционным предложением, Такое представ-

ление напоминает ветви дерева, Каждая полная ветвь ассоциируется с какой-то од-

ной из возможных последовательностей денежных потоков,

Один из способов решения этой задачи заключается в использовании де-

рева вероятностей (probability tree). Дерево вероятностей представляет собой

графический или табличный подход к организации возможных последова-

тельностей денежных потоков, генерируемых в ходе реализации инвестици-

онного проекта. В этом случае мы указываем вероятные будущие денежные

потоки рассматриваемого проекта в их взаимосвязи с результатами предыду-

щих периодов. Так мы можем учесть в нашем анализе корреляцию денежных

потоков, относящихся к разным периодам времени. Если, например, оказыва-

ется, что рассматриваемый проект характеризуется хорошим (высоким) де-

нежным потоком в первый период, то имеются неплохие шансы,, что он будет

характеризоваться хорошими денежными потоками и в последующие перио-

ды. Однако, несмотря на то что подобная связь между тем, что происходит

один период, и тем, что происходит в последующие периоды, наблюдается

достаточно часто, мы все же не можем быть полностью уверены в ней. Если

считается, что денежные потоки в разные периоды времени никак не связаны

между собой, то мы просто указываем распределение вероятностей величин

денежных потоков в разные периоды времени. Если такая взаимосвязь все же

существует, ее обязательно следует учитывать.

При использовании дерева вероятностей мы пытаемся представить ход бу-

дущих событий. На рис. 14.3 показано дерево вероятностей для проекта, рас-

считанного на два периода. Каждая полная ветвь представляет одну возмож-

ную последовательность денежных потоков. Для каждой из девяти ветвей, по-

казанных на этом рисунке, денежные потоки и соответствующие им

вероятности пронумерованы. Из рисунка видно: если результат за период 1

очень хороший (мы оказываемся на 500-долларовой ветви), это приводит нас к

совершенно иной совокупности возможных результатов за период 2 (800, 500

или 200 долл.), чем в случае, если бы период 1 оказался для нас очень небла-

гоприятным (когда мы оказываемся на ветви, соответствующей -100 долл.).

Следовательно, в момент времени 0 дерево вероятностей представляет нашу

наилучшую оценку того, что, видимо, произойдет в будущем, если за основу

берутся более ранние события (имевшие место в предшествующие периоды).

Глава 14. Риск и управленческие опционы.

623

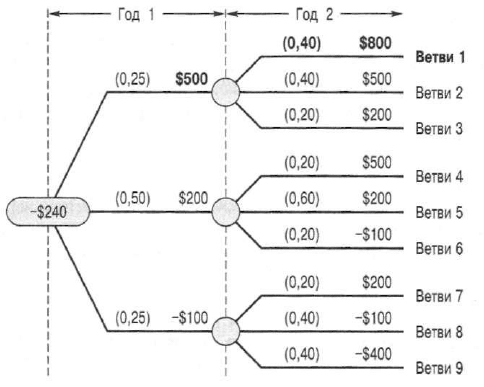
Рис. 14

.3. Графическое представление дерева вероятностей,

свидетельствующее о том, что денежные потоки за второй год

умеренно коррелированы с денежнььчи потоками за первый год;

например, вероятнее (но не гарантировано), что у нас будет

хороший денежный поток за второй год, если отмечался хоро-

ший денежный поток за первый год

ДЛЯ первого периода величина денежного потока не зависит от того, что

происходило раньше. Следовательно, вероятность, связанную с начальным

участком каждой полной ветви, называют начальной вероятностью {initial

probability). Однако величина денежного потока за второй период зависит от

того, что происходило раньше. Следовательно, вероятности, связанные с по-

следующими периодами, называют условными вероятностями {conditional

probabilities). Наконец, совместная вероятность (joint probability) представ-

ляет собой вероятность возникновения какой-то конкретной последователь-

ности денежных потоков. Чтобы проиллюстрировать эти понятия, обратимся

к нашему примеру проекта, рассчитанного на два периода.

Допустим, что мы изучаем возможность реализации инвестиционного проек-

та, представленного на рис. 14.3 (этот проект требует первоначальных инвести-

ций в размере 240 долл.). Учитывая результирующий денежный поток за пер-

вый год в размере 500 долл., условная вероятность того, что за второй год мы

получим 800 долл., равняется 40% (вероятность того, что денежные поступле-

ния составят 500 долл. равняется 40%, а вероятность того, что денежные посту-

пления составят 200 долл., — 20%). Совместная вероятность того, что денежные

поступления за первый год в размере 500 долл. будут сопровождаться денеж-

ными поступлениями за второй период в размере 800 долл. (т.е. вероятность пу-

ти, денежные потоки которого выделены жирным шрифтом, или ветви 1), пред-

ставляет собой произведение начальной вероятности на соответствующую ус-

ловную вероятность: 0,25 х 0,40 = 0,10 (см. табл. 14.1).

624 Часть V. Инвестиции в основной капитал

Аналогично этому совместная вероятность того, что денежный поток за

первый год в размере 500 долл. будет сопровождаться денежным потоком за

второй период в размере 500 долл., равняется 0,25 х 0,40 = 0,10, а совместная

вероятность того, что денежный поток за первый год в размере 500 долл. будет

сопровождаться денежным потоком за второй период в размере 200 долл.,

равняется 0,25 х 0,20 = 0,05. Если величина денежного потока за первый год

равняется 200 долл., тогда вероятность того, что денежный поток за второй

период составит 500 долл., равняется 0,20; 200 долл. — 0,60; а минус 100

долл. — 0,20. Точно так же мы можем вычислить совместные вероятности для

трех полных ветвей, показанных на этом рисунке. Они равняются соответст-

венно 0,10, 0,30 и 0,10. Аналогично можно определить совместные вероятно-

сти для последней совокупности из трех полных ветвей, где чистый денежный

поток за первый год равняется -100 долл.

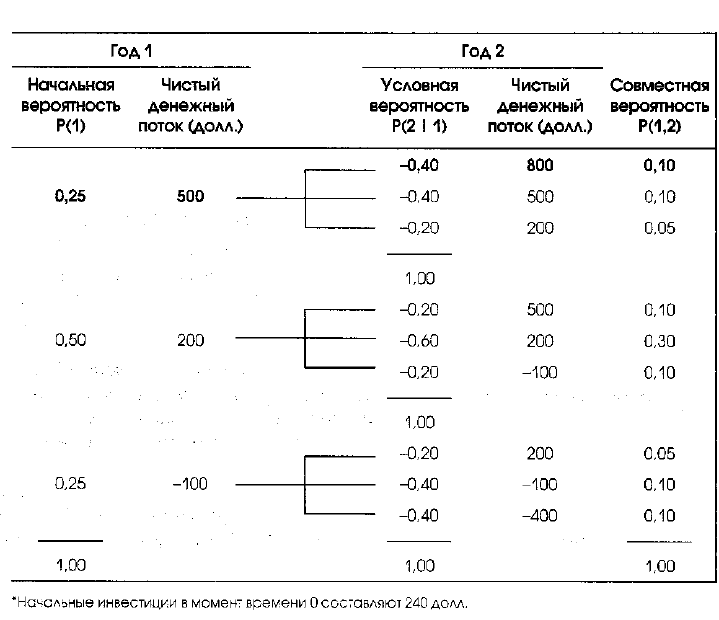
Таблица 14.1. Табличное представление дерева вероятностей*

'Начальные инвестиции в момент времени 0 составляют 240 долл.

Вычисление приведенной стоимости при безрисковой ставке. В преды-

дущей главе мы вычисляли единственное значение чистой приведенной стоимо-

сти для каждого проекта, дисконтируя денежные потоки с использованием тре-

буемой минимальной ставки доходности, которая "корректировала" будущие

денежные потоки как с учетом зависимости стоимости денег от времени, так и с

учетом риска. Однако, используя дерево вероятностей, мы пытаемся собрать

информацию по всему распределению вероятностей различных величин чистой

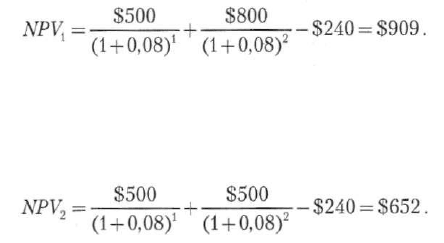
Глава 14. Риск и управленческие опционы.

625

приведенной стоимости. На этой стадии мы не станем делать "поправку на

риск", а просто выявим степень этого риска. Таким образом, мы выполняем дис-

контирование различных денежных потоков до их приведенной стоимости при

безрисковой ставке (risk-free rate). Эту ставку мы используем потому, что в под-

ходе, основанном на дереве вероятностей, путем дисконтирования мы пытаемся

отмежеваться от фактора зависимости стоимости денег от времени и анализиру-

ем отдельно фактор риска. Включение "надбавки за риск" в ставку дисконтиро-

вания — применительно к данному методу — приведет к двойному учету риска.

Сначала мы вводим поправку на риск в процессе дисконтирования, а затем —

еще раз — при анализе дисперсии распределения вероятностей возможных ве-

личин чистой приведенной стоимости. Именно поэтому в процессе дисконтиро-

вания следует использовать понятие безрисковой ставки.

Вернемся к нашему примеру. Ожидаемое значение распределения вероят-

ностей возможных величин чистой приведенной стоимости вычисляется по

формуле

NPV = Y,(NPV

)(P

), (14.3)

где NPV

— чистая приведенная стоимость, вычисленная при безрисковой ставке

для i'-й последовательности денежных потоков (полная ветвь денежного пото-

ка i), P

— совместная вероятность возникновения этой последовательности де-

нежных потоков, z — общее количество полных последовательностей денежных

потоков (или ветвей). В нашем случае имеется девять возможных последова-

тельностей чистых денежных потоков, поэтому 2 = 9. Первая последователь-

ность (ветвь) представлена чистым денежным потоком, равным -240 долл.

в момент времени 0, 500 долл. — за первый год и 800 долл. — за второй. Совме-

стная вероятность возникновения этой последовательности денежных потоков

равна 0,10. Если безрисковая ставка, которую мы используем в качестве ставки

дисконтирования, равняется 8%, то чистая приведенная стоимость этой кон-

кретной последовательности денежных потоков будет равняться:

$500 $800 _ $240 = $909.

(1 + 0.08)

(1 + 0,08)

Вторая последовательность денежных потоков будет представлена чистым

денежным потоком, равным -240 долл. в момент времени 0, 500 долл. — за

первый год и 500 долл. — за второй год. Чистая приведенная стоимость этой

последовательности денежных потоков составит:

$50

° +

$50

° - - $240 = $652.

Точно так же можно определить величины чистой приведенной стоимости

для семи других последовательностей денежных потоков. Если эти величины

умножить на соответствующие им совместные вероятности возникновения

(последний столбец в табл. 14.1), а затем просуммировать, получим ожидае-

мое значение чистой приведенной стоимости (с учетом распределения веро-

626 Часть V. Инвестиции в основной капитал

ятностей возможных величин чистой приведенной стоимости), округленное

до ближайшего целого числа. Соответствующие вычисления представлены

в табл. 14.2, из которой следует, что ожидаемое значение чистой приведенной

стоимости равняется 116 долл.

Важно отметить, что положительное ожидаемое значение чистой приве-

денной стоимости ( NPV) нельзя использовать как очевидное свидетельство

приемлемости соответствующего проекта. Это объясняется тем, что мы еще не

сделали поправку на риск. По той же причине ожидаемое значение чистой

приведенной стоимости не свидетельствует об увеличении стоимости фирмы,

если бы рассматриваемый проект был принят. Правильное значение NPV, ко-

торое можно использовать для этой цели, требует, чтобы ожидаемые денеж-

ные потоки для каждого периода были дисконтированы с необходимой мини-

мальной ставкой доходности, в которой учитывался бы риск инвестиционного

проекта.

Вычисление стандартного отклонения. Стандартное отклонение рас-

пределения вероятностей возможных величин чистой приведенной стоимо-

сти, aNPV, можно определить по формуле

J2(

NPV

i-NPV)

(Р^ . (14.4)

Приведенные выше определения переменных остаются в силе. Стандарт-

ное отклонение для нашего примера равно:

Таблица 14.2. Вычисление ожидаемого значения чистой приведенной

стоимости для рассматриваемого примера

Последовательность Чистая приведенная Совместная вероятность (2)х(3)

денежных потоков стоимость (долл.) возникновения (долл.)

(1) (2) (3) (4)

1 909 0,10 91

2 652 0,10 65

3 394 0,05 20

4 374 0,10 37

5 117 0,30 35

6 -141 0,10 -14

7 -161 0,05 -8

8 -418 0,10 -42

9 -676 0,10 -68

Средневзвешенное =

116 долл. =

NPV

Глава 14. Риск и управленческие опционы.

627

NPV

=[($909-$116)

(0Д0) + (-$652-$116)

(0,Ю)

+(394 -116)

(0,05) + (374 -116)

(0,10)

+(117 -11 б)

(0,30) + (-141 -11 б)

(0,10)

+(-161 -116)

(0,05) + (-418 -116)

(0Д 0)

+(-676-116)

(0,10)f

=[$197,277f

=$444

Округляя полученный результат до ближайшего целого числа, получаем ожи-

даемое значение чистой приведенной стоимости нашего проекта, равное 116 долл.,

и стандартное отклонение, равное 444 долл. Несмотря на то что вычисление средне-

квадратического отклонения в простейших случаях особой проблемы не представ-

ляет, этого нельзя сказать о более сложных ситуациях. Тогда на помощь может

прийти имитационное моделирование, которое позволяет получить приближенное

значение среднеквадратического отклонения.

Подход, основанный на имитационном

моделировании

Рассматривая возможность рискованных инвестиций, можно также восполь-

зоваться имитационным моделированием для поиска приближенных величин

ожидаемого значения (математического ожидания) чистой приведенной стоимо-

сти, ожидаемого значения IRR инвестиций или ожидаемого значения коэффици-

ента прибыльности, а также отклонения от ожидаемого значения. Под имитаци-

онным моделированием (simulation) мы понимаем проверку (тестирование) воз-

можных результатов реализации инвестиционного предложения еще до того, как

оно будет принято. Само это тестирование основывается на некоторой модели

в сочетании с соответствующей вероятностной информацией. Используя имита-

ционную модель, впервые предложенную Дэвидом Герцем, можно учесть, напри-

мер, перечисленные ниже факторы, которые оказывают влияние на последова-

тельность денежных потоков рассматриваемого проекта

Анализ рынка

1. Величина рынка.

2. Продажная цена.

3. Темпы роста рынка.

4. Доля рынка (от которой зависят физические объемы продажи).

Анализ инвестиционных затрат

5. Требуемые инвестиции.

6. Продолжительность жизненного цикла производственных мощностей.

7. Остаточная стоимость инвестиций.

David В. Hertz, "Risk Analysis in Capital Investment", Harvard Business Review 42 (January-February

1964), p. 95-106.

628 Часть V. Инвестиции в основной капитал

Эксплуатационные и фиксированные расходы

8. Эксплуатационные издержки.

9. Постоянные издержки.

Каждому из этих факторов приписываются соответствующие распределе-

ния вероятностей, основанные на оценке руководством фирмы возможных ре-

зультатов. Таким образом, последние отображаются по каждому фактору в со-

ответствии с вероятностями их появления. После того как мы определим рас-

пределения вероятностей, нашей следующей задачей будет нахождение IRR

инвестиций (или чистой приведенной стоимости, вычисленной при безриско-

вой ставке), выступающего результатом произвольного сочетания перечис-

ленных выше девяти факторов.

Чтобы проиллюстрировать процесс имитационного моделирования, допус-

тим, что фактор "Величина рынка" характеризуется следующим распределе-

нием вероятностей.

Величина рынка

(тыс. единиц)

450 500 550 600 650 700 750

Вероятность появления 0,05 0,10

0,20

0,30 0,20

0,10

0,05

Допустим теперь, что перед нами колесо рулетки с сотней пронумерован-

ных ячеек, причем номера от 1 до 5 представляют рынок величиной 450 тысяч

единиц, от 6 до 15 — 500 тысяч единиц, от 16 до 35 — 550 тысяч единиц и т.д.

до 100. Как и в обычной рулетке, мы вращаем колесо и шарик попадает в одну

из ста пронумерованных ячеек. Допустим, что шарик попал в ячейку под но-

мером 26. Таким образом, в этом испытании мы промоделировали рынок ве-

личиной 550 тысяч единиц. К счастью, чтобы выполнить моделирование, ру-

летка нам не понадобится. Примерно то же самое можно проделать на компь-

ютере — только гораздо эффективнее.

Испытания в имитационном моделировании выполняются по каждому из

остальных восьми факторов. В совокупности, первые четыре фактора (анализ

рынка) позволяют нам выяснить ежегодные объемы продаж. Факторы 8 и 9

показывают ежегодные величины эксплуатационных и постоянных издержек.

В совокупности, на основании этих шести факторов, мы вычисляем ежегод-

ные приростные доходы (выручку) компании. Если данные испытаний по

этим шести факторам объединить с данными испытаний, касающихся необхо-

димых инвестиций, продолжительности жизненного цикла производственных

мощностей и остаточной стоимости инвестиционного проекта, то у нас поя-

вится достаточно информации для вычисления IRR инвестиций (или чистой

приведенной стоимости) для соответствующего испытания в ходе имитаци-

онного моделирования. Таким образом, компьютер моделирует данные испы-

таний по каждому из перечисленных нами девяти факторов, а затем вычисля-

ет внутреннюю ставку доходности инвестиций исходя из промоделированных

значений. Этот процесс повторяется многократно. Каждый раз мы получаем

то или иное сочетание значений для девяти факторов и внутреннюю доход-

ность инвестиций, соответствующую этому сочетанию. Если данный процесс

повторяется достаточно часто, у нас появляется возможность построить гра-

Глава 14. Риск и управленческие опционы

629

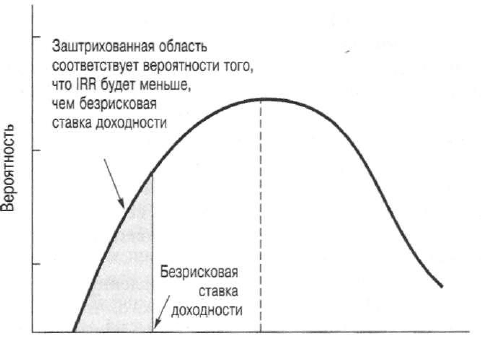
фик распределения вероятностей (частот появления) для IRR инвестиций,

подобный показанному на рис. 14.4. С помощью этого графика распределения

вероятностей можно найти ожидаемую величину внутренней доходности ин-

вестиций и разброс относительно этой ожидаемой величины.

Использование информации о распределении

вероятностей

Ожидаемое значение и стандартное отклонение распределения вероятно-

стей возможных величин чистой приведенной стоимости (или, как альтерна-

тивный вариант, IRR инвестиций) — независимо от того, каким путем они бы-

ли получены: с помощью дерева вероятностей, имитационного моделирования

или каким-то иным способом, — предоставляют в наше распоряжение доста-

точно информации, чтобы оценить риск рассматриваемого инвестиционного

предложения. Если, например, распределение вероятностей возможных вели-

чин чистой приведенной стоимости близко к нормальному, мы можем вычис-

лить вероятность того, что реализация проекта обеспечит чистую приведен-

ную стоимость меньше (или, наоборот, больше) некоторого указанного значе-

ния. Эту вероятность можно найти, вычислив площадь области под кривой

распределения вероятностей слева (или справа) от интересующей нас точки.

Внутренняя ставка доходности инвестиций (%)

Рис. 14.4. Распределение вероятностей для внутренней став-

ки доходности инвестиций

Обратимся к результатам, полученным нами ранее с помощью дерева вероят-

ностей (предполагается нормальное распределение вероятностей). Допустим, мы

хотим определить вероятность того, что чистая приведенная стоимость окажется

меньше нуля. Чтобы определить эту вероятность, мы сначала определяем, на

сколько величин стандартного отклонения отстоит нуль от ожидаемого значения

чистой приведенной стоимости для рассматриваемого проекта (116 долл.). Для

этого мы определяем разницу между нулем и 116 долл., а затем нормализуем эту

разницу, деля ее на стандартное отклонение возможных величин чистой приве-

денной стоимости. Общая формула имеет следующий вид:

630 Часть V. Инвестиции в основной капитал

_NPV*-NPV

(145)

°NPV

где Z ("Z-балл") говорит о том, на сколько величин среднеквадратического от-

клонения отстоит NPV* (именно этот результат нас интересует) от ожидаемого

значения; NPV — ожидаемое значение чистой приведенной стоимости; a q

—

стандартное отклонение распределения вероятностей. В нашем случае

z =

«116

$444

Полученный результат свидетельствует о том, что нулевое значение чистой

приведенной стоимости отстоит на 0,26 стандартного отклонения от ожидаемо-

го значения распределения вероятностей возможных величин чистой приведен-

ной стоимости (по левую сторону от него). (Отрицательное значение Z-балла го-

ворит о том, что мы находимся по левую сторону от среднего значения.)

Чтобы вычислить вероятность того, что чистая приведенная стоимость ин-

вестиционного проекта окажется меньше нуля, обратимся к таблице нормаль-

ного распределения вероятностей (см. табл. V Приложения, помещенного

в конце книги). С ее помощью мы находим, что в случае нормального распре-

деления вероятность того, что какое-то наблюдение будет отстоять на 0,25

среднеквадратического отклонения по левую сторону от ожидаемого значения

для этого распределения, равняется 0,4013. Вероятность того, что оно будет

отстоять от ожидаемого значения более чем на 0,30 среднеквадратического

отклонения, равняется 0,3821. Выполняя интерполяцию, находим, что суще-

ствует примерно 40%-ная вероятность того, что чистая приведенная стои-

мость инвестиционного предложения не превысит нулевого значения. Следо-

вательно, нам также известно, что существует 60%-ная вероятность того, что

чистая приведенная стоимость инвестиционного предложения окажется

больше нуля. Выражая отклонения от ожидаемого значения в виде средне-

квадратических отклонений, можно вычислить вероятность того, что чистая

приведенная стоимость инвестиционного предложения окажется больше или

меньше некоторой заданной величины

Проблемы с интерпретацией. Хотя перечисленные выше процедуры да-

ют нам возможность вычислить вероятность того, что чистая приведенная

стоимость окажется меньше некоторого заданного значения (например, нуля),

полученные результаты иногда с трудом поддаются интерпретации. Это объ-

ясняется тем, что чистая приведенная стоимость, как вы, наверное, помните,

вычисляется при безрисковой ставке, а не при требуемой минимальной ставке

доходности соответствующего проекта. Так что же мы на самом деле имеем в

виду, когда, например, говорим, что вероятность отрицательной величины

чистой приведенной стоимости равняется 40%?

В этих примерах мы предполагали соблюдение условия нормального распределения. Несмотря на

то что соблюдение этого условия очень желательно для удобства вычислений, оно не является

обязательным для использования описываемого нами подхода. Даже когда распределение не явля-

ется нормальным, мы, как правило, можем делать относительно "сильные" вероятностные выво-

ды, используя неравенство Чебышева, которое накладывает определенный верхний предел на ту

часть значений, которая относится к "хвостам" любого распределения.