Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

7.10. МЕМБРАНЫ ФОТОРЕЦЕПТОРОВ

391

Если

зависимость дихроизма

от

времени действительно опре-

деляется вращательной диффузией,

то

справедливо уравнение

1¥

~дГ'

(7Л2)

где

— доля хромофоров, ориентированных

интервале

углов

от

9 до 9 -f-

dQ,

х —

время релаксации.

Для

линейного хромо-

форма

вращательной диффузии вокруг оси, перпендикулярной

мембране диска, решение

(7.12)

имеет вид

tt=l

fexp(-4//t)cos29.

(7.13)

Время

измеряется

от

начала вспышки, 9 —

угол,

образуемый

хромофором

электрическим вектором вспышечного света,

—

эмпирический множитель. Дихроичное отношение равно

п/2

[ n(6)cos

9rfe

_0 2 + /ехр(-4//т) .....

"/2

~ 2 - f

ехр

4//т)

* '

(6) sin

В идеальных условиях, когда

/= 1,

максимальное начальное

отношение

равно

что отвечает значению, найденному для сет-

чатки,

фиксированной глутаровым альдегидом [164].

импульс-

ных опытах это отношение получалось равным

2, что

отвечает

0,7. Значение времени вращательной диффузии

зависит

от вязкости среды

ц, ее

температуры,

также

от

размеров хро-

мофорной

молекулы. Согласно Эйнштейну,

для

сферы радиуса

г,

испытывающей броуновское вращение вокруг некоторой оси,

(7.15)

При

20 °С

для родопсина имеет значение около

мкс,

г =

22—28

А, родопсин приближенно сферичен

погружен

мем-

брану. Отсюда

следует,

что вязкость мембраны

г)

около

пуаз

(интервал

от 0,7 до 6

пуаз),

т.

е. она близка

вязкости легкого

масла (такого,

как

оливковое). Мембрана оказывается весьма

жидкой.

Это

согласуется

другими данными

подвижности

мембран, например,

результатами изучения поступательной

диффузии флуоресцирующих антител, присоединенных

анти-

генам

на

поверхностях некоторых клеток [167].

этих случаях

также получились значения г] порядка

—10 пуаз (ср.

3.8).

В той

же

работе Кона [166] обсуждается вопрос

функцио-

нировании

родопсина

качестве диффузионного переносчика.

По-видимому, при поворотах молекулы родопсина, возникающих

392 ГЛ. 7. ФОТОБИОЛОГИЧЕСКИЕ ПРОЦЕССЫ

вследствие его конформационных превращений, меняется сте-

пень

погружения родопсина в жидкую билипидную мембрану,

что существенно для изменения ее ионной проницаемости

(см.

[168]).

Позднее удалось наблюдать и латеральную диффузию ро-

допсина в мембране [169]. Измерения проводились в выделен-

ных палочках методом импульсного фотолиза и микроспектро-

фотометрии. Изучалось перераспределение выцветшего и невы-

цветшего родопсина. Найденная константа диффузии D для

палочек из сетчатки лягушки равна 3,5 ± 1,5• 10—

см

-с~'.

Вязкость мембраны, вычисляемая по формуле

оказалась лежащей в том же интервале значений 1—4 пуаз.

Время

между

столкновениями соседних молекул родопсина

в сетчатке находится по формуле

4Dx

(7.17)

где s — расстояние

между

молекулами родопсина. Если

эффек-

тивный диаметр молекулы родопсина 45 А, а расстояние

между

центрами молекул 70 А, то s = 25 А и т

= 4 мкс, что в 5 раз

меньше времени релаксации вращательной диффузии. Частота

соударений составляет 10

— 10

-1

Эти результаты представляют большой интерес. Они

дают

основу для построения теории функционирования мембран, исхо-

дящей из их жидкостных свойств (ср. стр. 142). Мы еще очень

мало знаем о событиях, приводящих к возникновению нервного

импульса в фоторецепторной системе. Можно

думать,

что эти

события тесно связаны с поведением жидкой мембраны.

ГЛАВА 8

НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

§ 8.1.

ВВЕДЕНИЕ

Поведение динамической системы описывается физикой на

языке детерминистической теории, пользующейся дифферен-

циальными уравнениями.

Динамические системы линейны, если их кинетическое по-

ведение может быть представлено линейными дифференциаль-

ными

уравнениями, т. е. уравнениями, коэффициенты которых

не зависят от координат и скоростей. Иными словами, пред-

полагается, что параметры системы не зависят от ее состоя-

ния.

Почти

всегда

такое предположение есть идеализация,

однако для множества

задач

физики применение линейных

уравнений и законно, и целесообразно. Как показано в гл. 2,

в неравновесной термодинамике линейность означает прямую

пропорциональность

между

реакцией системы (потоками) и

действующей силой (обобщенные силы).

При

невыполнении условия независимости параметров от

состояния системы (в частности, постоянства феноменологиче-

ских коэффициентов в неравновесной термодинамике) система

оказывается нелинейной. Это — общий

случай

неидеализиро-

ванной

системы. Однако поведение нелинейной системы может

трактоваться на основе линейных законов при малых отклоне-

ниях от состояния равновесия или стационарного состояния.

Линеаризация уравнений есть обоснованный прием исследова-

ния

соответствующих

задач. Основные биологические явления

вообще не

могут

быть поняты на основе «линейной теории». Мы

уже встречались с существенно нелинейными процессами — с

генерацией и распространением нервного импульса, с мышеч-

ным сокращением и т. д. В этой и

следующей

главе

рассматри-

ваются процессы, связанные с упорядоченным поведением био-

логической системы в пространстве и времени.

Остановимся прежде всего на термодинамическом аспекте

проблемы. Как показано в

работах

Пригожина и его школы

[1—3, 123], линейная термодинамика, ограничивающаяся рассмо-

трением состояний, близких к равновесию, не может объяс-

нить возникновение упорядоченной системы при обычных (т. е.

не очень низких)

температурах.

Имеются две возможности

394 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

возникновения

порядка. Первая возможность чисто термодина-

мическая. Система не адиабатична, она находится в контакте

с тепловым резервуаром. Ее состояние характеризуется значе-

нием

свободной энергии, которая минимальна в равновесии.

Термодинамическое упорядочение связано с понижением

энер-

гии системы. Ему препятствует энтропийный вклад в свобод-

ную энергию. Однако при достаточно низкой

температуре

этот

вклад становится настолько малым, что более не мешает упо-

рядочению, и образуется равновесная упорядоченная система,

скажем, кристалл.

Очевидно, что эта возможность не реализуется в сложных

биологических системах. Вероятность возникновения термоди-

намической упорядоченности при физиологических

температу-

рах (в области 300 К) для системы, состоящей из макроскопи-

ческого числа разнообразных молекул, исчезающе мала. При

этих

температурах

должен превалировать термодинамический

беспорядок.

Имеется, однако, вторая возможность упорядочения — со-

здание порядка вдали от равновесия, кинетическое упорядоче-

ние,

возникновение

диссипативной

системы.

Когерентное пове-

дение такого рода возможно вне области стабильности состоя-

ний,

характеризуемых обычным термодинамическим поведением.

Критерием возможности возникновения упорядоченной диссипа-

тивной

структуры

является невыполнение условия устойчивости.

Приведем вновь основные соотношения неравновесной термо-

динамики (см. гл. 2). Функция диссипации равна

Ее изменение во времени записывается в виде

djo

dJ,

dX,

X+J

При

независимых от времени граничных условиях имеем

^Г<0. (8.3)

Отсюда

следует

условие устойчивости рассматриваемого ста-

ционарного состояния

£ 6J, 6Х, > 0, (8.4)

/•

где б/j, 8Xj — отклонения величин обобщенных потоков и сил

от их стационарных значений. Вблизи равновесия условие

S 8.1. ВВЕДЕНИЕ 395

(8.4) всегда выполняется. Применительно к химическим про-

цессам оно имеет вид

Ебиуб^Х). (8.5)

Если

условие (8.4) не выполняется, то стационарное состояние

не

устойчиво и возможно усиление флуктуации, приводящих к

возникновению

нетермодинамического порядка. «Порядок че-

рез флуктуации» возможен, очевидно, лишь в такой открытой

системе, поведение которой существенно нелинейно.

О каком порядке идет речь, к чему может приводить нели-

нейность

поведения системы? Прежде всего это возникновение

пространственного порядка, структуры, в пространственно го-

могенной

системе. Но нелинейности основных соотношений от-

ветственны и за упорядоченное поведение в-о времени, в част-

ности,

за незатухающие колебания системы.

В биологии мы встречаемся с тремя группами явлений, не-

посредственно свидетельствующих о нелинейности соответст-

вующих процессов.

Во-первых, это периодические, колебательные, явления. На

всех

уровнях организации (от макромолекулярного до популя-

ционного)

в биологических системах происходят незатухающие

колебания

характеристических физических параметров — фер-

ментативной активности, концентрации метаболитов, числен-

ности

популяции и т. д.

Во-вторых, поведение клеток и организмов на

всех

уровнях

организации

подлежит регуляции и контролю, определяемым

кооперативными

взаимодействиями, отсутствующими в линей-

ных системах.

В-третьих,

биологическая система, начиная с клетки и кон-

чая биосферой в целом, необратимо развивается, эволюциони-

рует.

Развитие означает возникновение новых структур, т. е.

процесс существенно нелинейный.

Остановимся,

прежде всего, на колебательных процессах.

Можно

привести весьма общие аргументы в пользу того, что

биологическая система должна быть колебательной [4]. Био-

логические системы являются результатом длительной эволю-

ции.

Устойчивые системы за время эволюции должны были

уравновеситься, стать частью среды. Напротив, неустойчивые

системы за это время распались. Следовательно, лишь систе-

мы,

внутреннее движение которых имеет колебательную при-

роду,

могли сохраниться.

Конечно,

это лишь качественное рассуждение, и научная

аргументация

требует

анализа временного поведения системы.

Но,

так или иначе, колебательные процессы чрезвычайно важ-

ны

в биологии. Гудвин предпринял попытку построить универ-

396 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

сальную теорию внутриклеточных регуляторных процессов, ис-

ходя из рассмотрения клетки как системы химических осцилля-

торов [5]. Считая эти осцилляторы почти независимыми, Гудвин

строит формальную статистическую механику такой системы,

вводя по аналогии с обычными физическими величинами услов-

ные

параметры — «таландическую

температуру»

и т. д. Обыч-

ные

понятия термодинамики заменяются условными вследствие

того, что в фазовом пространстве системы роль координат

играют концентрации метаболитов, а роль скоростей — скоро-

сти реакций. Колебания возникают благодаря наличию обрат-

ных связей. Эта концепция не может быть принята. Как уже

неоднократно

отмечалось выше, биологическая система не яв-

ляется статистической, но представляет собой «химическую ма-

шину». Введение статистики по Гудвину не меняет дела, так

как

статистическое рассмотрение возможно лишь для боль-

шого числа независимых химических осцилляторов, для

«газа»,

состоящего из таких осцилляторов. Но в действительности

клетка есть не

«газ»,

но «машина», и колебательные химиче-

ские

процессы в клетке взаимосвязаны и пространственно орга-

низованны.

другой

стороны, гораздо более строгий и общий

подход

к рассмотрению биологических систем основывается на

неравновесной

термодинамике, пользующейся обычными фи-

зическими

понятиями. Убедительная критика теории Гудвина

дана Молчановым [6].

Из

термодинамического рассмотрения открытых систем, на-

ходящихся вдали от равновесия,

следует

необходимость изуче-

ния

их стационарных состояний, которые

могут

быть множест-

венными

[7]. Необходимо исследовать устойчивость этих со-

стояний

и условия переходов

между

ними.

В сущности, термодинамика здесь кончается, и научная

трактовка нелинейных процессов состоит в их рассмотрении,

основанном

не на общих термодинамических свойствах систем,

но

на конкретных кинетических моделях, изучаемых посредст-

вом аппарата дифференциальных уравнений. Вопрос о его при-

менимости для биологических систем не тривиален.

«Химическая машина», вообще говоря, характеризуется не

непрерывным,

но дискретным набором состояний. Применение

аппарата дифференциальных уравнений к такой системе озна-

чает включение дискретных состояний в некоторое непрерыв-

ное

множество. Такая процедура не препятствует трактовке по-

ведения дискретной системы, напротив, она позволяет при над-

лежащем выборе модели его проанализировать (см. [4]). Вместе

с тем аппарат дифференциальных уравнений может оказаться

недостаточным для исследования стохастических процессов, тре-

бующих применения теории вероятностей, теории цепей Мар-

кова.

Вопрос о математическом методе должен решаться от-

8.2.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ

ОСНОВЫ

КИНЕТИКИ

397

дельно для каждого класса моделей. Само моделирование опре-

деляется не столько объектом исследования, сколько изучаемым

процессом,

и непосредственно зависит от шкалы времени, в ко-

торой этот процесс развивается. В любой биологической системе

происходит множество нелинейных кинетических процессов, ха-

рактеризуемых собственными временами.

В этой и

следующей

главах

приведено модельное рассмотре-

ние

характерных для биологии колебательных, регуляторных и

эволюционных процессов. Основным методом является исследо-

вание

кинетических уравнений, описывающих модель, но в ряде

случаев

такое исследование должно быть дополнено решением

соответствующих

стохастических задач.

Общее рассмотрение этих проблем дано также в моногра-

фии

Романовского, Степановой, Чернавского [18].

8.2.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ

ОСНОВЫ

КИНЕТИКИ

НЕЛИНЕЙНЫХ

ПРОЦЕССОВ

Определим

метод

изучения биологической системы как пост-

роение кинетической модели и описание модели дифференциаль-

ными

уравнениями, т. е. как построение математической модели

исследование решений этих уравнений.

Достаточно общая форма математической модели имеет вид

~~jf~

'i \

• •

•)

ю>

~dl~ — FN (*i.

• • •

N)>

(8.6)

где

Х\, ..., x

—

физические переменные, характеризующие

си-

стему

зависящие

от

времени

начальных условий,

F\, ...

...,

— в

общем

случае

нелинейные функции

от

этих пере-

менных.

Систему

(8.6)

можно линеаризовать. Ищутся стационарные

значения

переменных

х°

{

, ..., x°

являющиеся решениями урав-

нений

(8.6) при к\ = ... = x

= 0.

Далее исследуются линей-

ные уравнения, записанные

переменных, представляющих

со-

бой малые отклонения

—х°

..., a

— x

— x°

;

членами,

нелинейными

относительно

аи

можно пренебречь.

большин-

стве

случаев

для

интересующих

нас

задач оказывается возмож-

ным

ограничиться системами второго порядка

(N = 2) (см.

[18]

[]

В соответствии

со

сказанным целесообразно начать изложе-

ние

исследования простой линейной модели

—

осциллятора

398 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

с трением. Его уравнение движения есть уравнение второго по-

рядка

тх + bx + kx = 0, (8.7)

которое можно представить в форме

двух

уравнений первого

порядка,

если ввести

вторую

переменную — скорость у = х.

Тогда получим линейные уравнения типа (8.6)

* = У, 6 — ±У~*- (8-8)

Общее

решение

уравнения

(8.7)

есть

х = А

ехр Я,/ + А

ехр l

t, (8.9)

где Xi и Я

—

корни

квадратного

уравнения

При

> 4km эти корни вещественны, при Ъ

< Akm — ком-

плексны.

В первом

случае

процесс имеет характер апериодиче-

ского затухания, во втором —

затухающих

колебаний. Значе-

ния

А\ и Л2 определяются начальными условиями.

Рациональный

метод исследования кинетической системы со-

стоит в получении ее «фазового портрета». Движение системы

представляется движением изображающей точки на фазовой

плоскости х, у, где у = х. Точка движется по фазовой траекто-

рии

с фазовой скоростью. Получим уравнение фазовой траекто-

рии

для осциллятора с трением, исключив время из уравнений

(8.8). Для этого разделим второе уравнение на первое:

где 2h = b/m,

ю^

= /г//п. Уравнение

(8.11)

описывает интеграль-

ные

кривые, в каждой точке которых касательная имеет наклон,

равный

dy/dx. Вместе с уравнением (8.8) уравнение

(8.11)

опре-

деляет на фазовой плоскости некоторое векторное поле с един-

ственной

особой точкой х = 0, у = 0. Удобно исследовать это

поле с помощью

изоклин,

т. е. кривых (в данном

случае

прямых),

являющихся геометрическим местом точек, в которых касатель-

ные

ко всем интегральным кривым имеют одинаковый наклон.

В нашем

случае

уравнение изоклины с наклоном х имеет вид

dy _

dx ~

или

8Л2

8.2. ФИЗИКО-МАТЕМАТИЧЕСКИЕ ОСНОВЫ КИНЕТИКИ

399

Иными

словами, изоклины представляют собой прямые, прохо-

дящие через начало координат — через особую точку х = О,

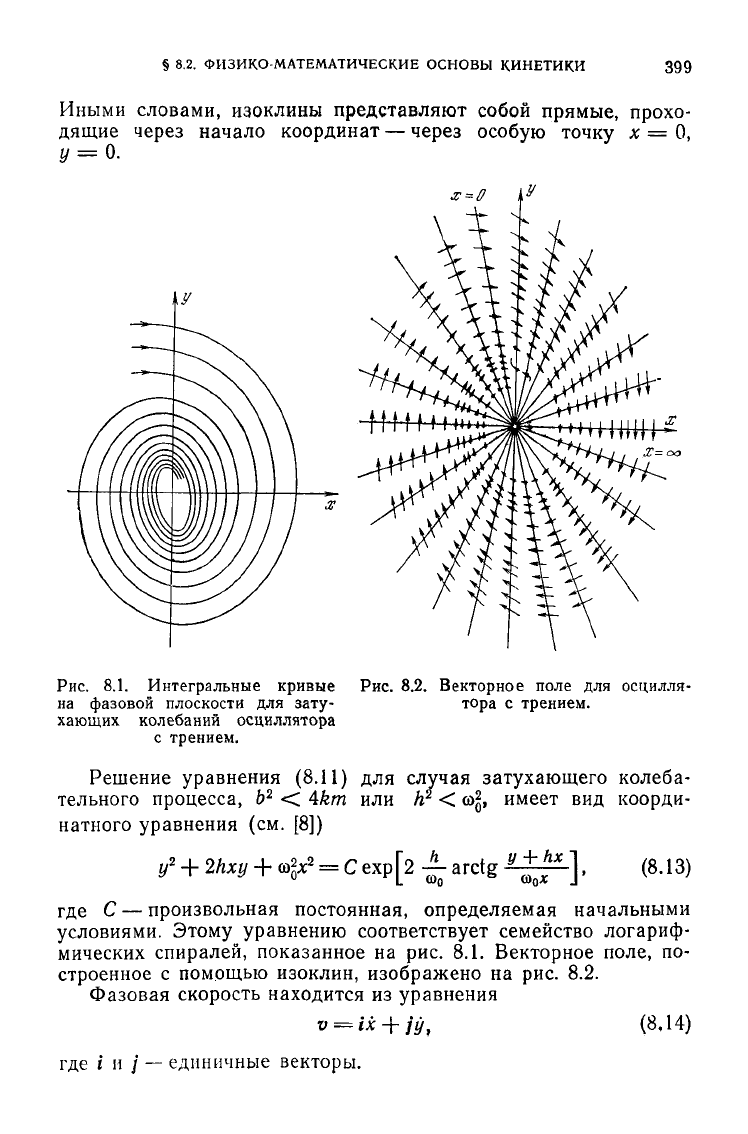
Рис.

8.1. Интегральные кривые

на

фазовой плоскости для

зату-

хающих колебаний осциллятора

с трением.

Рис.

8.2. Векторное поле для осцилля-

тора с трением.

Решение уравнения

(8.11)

для случая

затухающего

колеба-

тельного процесса, b

< 4km или /г<со

, имеет вид коорди-

натного уравнения (см. [8])

г/

+ 2/ш/ + со

Сехр[2

±arctg

(8.13)

где С — произвольная постоянная, определяемая начальными

условиями. Этому уравнению соответствует семейство логариф-

мических спиралей, показанное на рис. 8.1. Векторное поле, по-

строенное с помощью изоклин, изображено на рис. 8.2.

Фазовая скорость находится из уравнения

v = ix + jy,

(8.14)

где i и / — единичные векторы.

400 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

В нашем случае, согласно уравнениям (8.8),

\v\

4/г

)

Фазовая

скорость убывает по мере приближения к началу коор-

динат и обращается в нуль в этой точке.

При

h = 0 (т. е. Ь = 0) трения нет, и система становится

незатухающим гармоническим осциллятором. Интегральные

кривые представляют се-

мейство эллипсов

г/

-+-

со2х

= const (8.15)

(см.

[8], а также [9], § 1.2).

Уравнение изоклин имеет

вид у=—coj-x/x, фазовая ско-

рость задается

ниями

v — iy —

соотноше-

I 7, |2 =

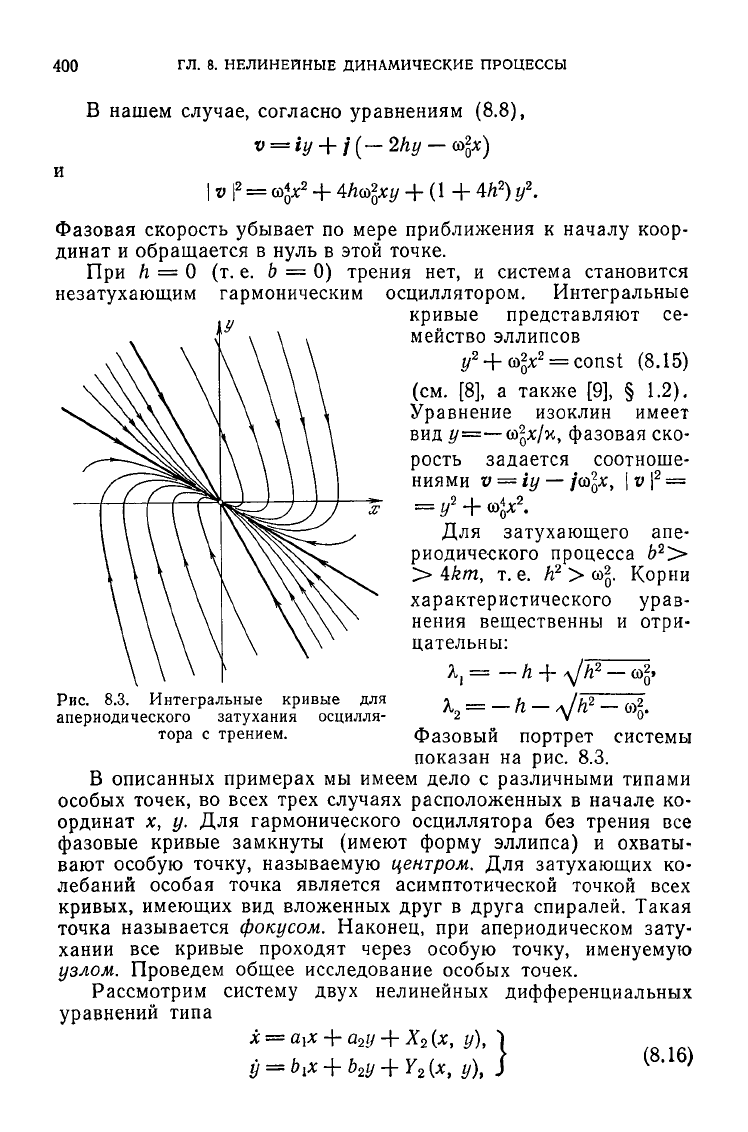
Для затухающего апе-

риодического процесса Ь

> 4km, т. е. h

> со

. Корни

характеристического урав-

нения

вещественны и отри-

цательны:

Рис.

8.3. Интегральные кривые для Я, = h -

апериодического затухания осцилля- 2

тора с трением. Фазовый портрет системы

показан

на рис. 8.3.

В описанных примерах мы имеем дело с различными типами

особых точек, во всех трех случаях расположенных в начале ко-

ординат х, у. Для гармонического осциллятора без трения все

фазовые кривые замкнуты (имеют форму эллипса) и охваты-

вают особую точку, называемую

центром.

Для затухающих ко-

лебаний особая точка является асимптотической точкой всех

кривых, имеющих вид вложенных

друг

друга

спиралей. Такая

точка называется

фокусом.

Наконец, при апериодическом

зату-

хании все кривые проходят через особую точку, именуемую

узлом.

Проведем общее исследование особых точек.

Рассмотрим систему

двух

нелинейных дифференциальных

уравнений типа

х = а

х + а

у + Х

[х, у), \

-Y

(х и) J ( '

2 \

> У), J