Волькенштейн М.В. Общая биофизика
Подождите немного. Документ загружается.


§
8.3 АВТОКАТАЛИТИЧЕСКИЕ
ХИМИЧЕСКИЕ
СИСТЕМЫ
411
Единственное стационарное решение отвечает условию X —
=
Y = 0. Имеем
Модель Лотка сходна с моделью «хищник — жертва», исследо-
ванной
Вольтерра [25] (подробный анализ см. также в [26]).
В некотором замкнутом районе живут хищники и их жертвы,
скажем, рыси и зайцы. Рыси питаются только зайцами, зайцы
питаются растительной пищей, имеющейся всегда в избытке.
Число жертв Х\, число хищников Х
2
. Изменения численности по-
пуляций со временем описываются уравнениями
f
= kX kXX
Константа k\ характеризует размножение жертв, k — их убыль
вследствие встреч с хищниками, k' — размножение хищников,
для которого необходимо питание, т. е. встречи с жертвами,
к
2
— вымирание хищников. Все коэффициенты k\, k, k', k
2
поло-
жительны.
Проведем рассмотрение системы Вольтерра — Лотка в этом
простом случае (см. [1, 19, 26], а также [8], стр. 164). Найдем
стационарные значения Х° и Х%. Из уравнений (8.40) при
Xi = Х
2
= 0 получаем
X\ = k
2
jk\ Xl = kjk.
Представим значения X
it
X
2
в виде
X
l
=
X°expa
l
,
X
2
=
Z°expa
2
.
(8.41)
Очевидно, что а* =
1п(Х
г
/Х°)
являются мерой отклонения X
t
от стационарного состояния, в котором а,- = 0. Уравнения (8.40)
перепишутся в виде
(8.42)
Умножим первое уравнение на XJ(1—expa,), второе — на
— ехра
2
) и сложим:
i- Х^ (1 - ехр а,) + -Y Х\а
2
(1 - ехр а
2
) = 0, (8.43)
или
412
ГЛ. 8. НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ
т. е.
•J-
Х° (ехр а, - а,) + -~Х°
2
(ехр а
2
- а
2
) = К = const. (8.44)
Величина К есть постоянная движения. Оба члена в /( положи-
тельны, так как если а* > 0, то ехр
CCJ
> а*, а если а,- < 0, то
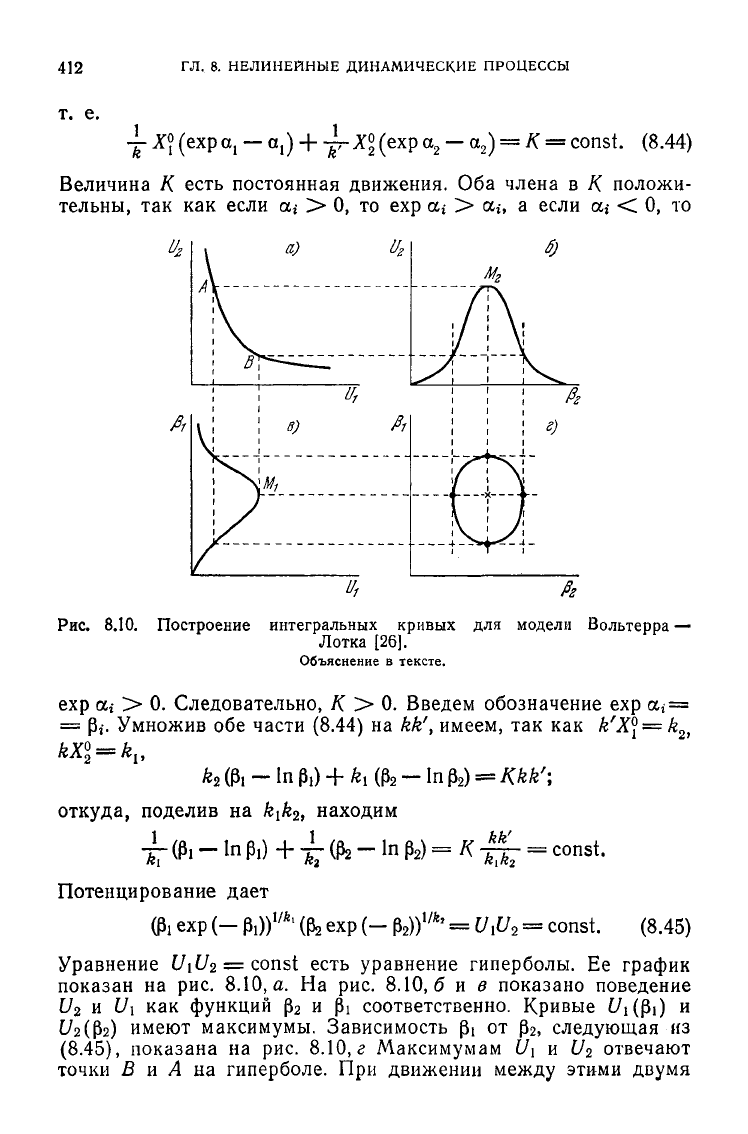
Рис.
8.10. Построение интегральных кривых для модели Вольтерра —
Лотка [26].
Объяснение в тексте.
ехр (Xi > 0. Следовательно, К > 0. Введем обозначение ехр а,=
=
р,-. Умножив обе части (8.44) на kk', имеем, так как
k
r
X°
l
= k
2t
k
2
(p, - In p,) + ft, (p
2
- In p
2
) = Kkk'\
откуда, поделив на kik
2
, находим
Ъ
(Р.
-
In
P.)
+
j;
(fe
-
In
p
2
)
= ^
-gfa
=
const.
Потенцирование
дает
(P,
ехр (-
p,))
I/ftl
(p, exp (-
p
2
))
1/ft
'
==
t/,f/
2
= const. (8.45)
Уравнение C/it/
2
= const есть уравнение гиперболы. Ее график
показан
на рис. 8.10, а. На рис.
8.10,6
и в показано поведение
U
2
и U\ как функций р
2
и р\ соответственно. Кривые
£/i(Pi)
и
£/
2
(р
2
)
имеют максимумы. Зависимость Pi от р
2
, следующая из
(8.45), показана на рис. 8.10, г Максимумам 11\ и U
2
отвечают
точки В и А па гиперболе. При движении между этими двумя
§
8.3 АВТОКАТАЛИТИЧЕСКИЕ
ХИМИЧЕСКИЕ
СИСТЕМЫ
413
предельными точками на плоскости ($ь р
2
описывается цикл.
Характер цикла зависит от начальных условий. Стационарному
состоянию
соответствуют
точки Л и В на гиперболе, точки мак-
симумов Mi и М
2
на кривых
£A(Pi)
и
^МРг)
и
особая точка типа
центра на плоскости Pi, р
2
. Определим поведение системы вблизи
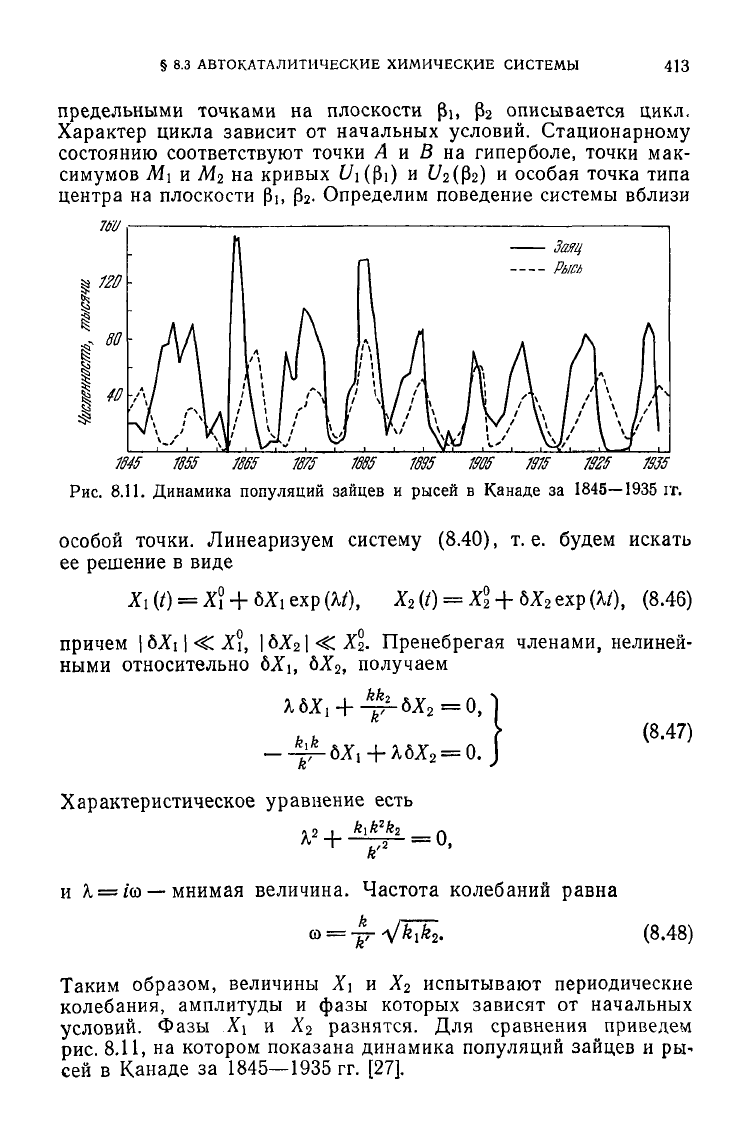
1845
1855 1855 1875 1885 1895 1905 1915 19Z5 1955
Рис.
8.П. Динамика популяций зайцев и рысей в Канаде за
I845—1935
гг.
особой точки. Линеаризуем систему (8.40), т.е.
будем
искать
ее решение в виде
Xi(0 = Z? +
6X
ieX
p(W),
X
2
{t) = Xl + 6X
2
exv(kl),
(8.46)
причем | bXi | <C X°i, | ЬХ
2
1 < X
2
. Пренебрегая членами, нелиней-
ными
относительно б^
ь
ЬХ
2
, получаем
(8.47)
Характеристическое уравнение есть
Я
2
+
*'
fe
?
2
=
О,
и
К = /со — мнимая величина. Частота колебаний равна
(8.48)
Таким образом, величины Х\ и Х
2
испытывают периодические
колебания, амплитуды и фазы которых зависят от начальных
условий. Фазы Х\ и Х
2
разнятся. Для сравнения приведем
рис.
8.11, на котором показана динамика популяций зайцев и ры-
сей в Канаде за
1845—1935
гг. [27].

414 ГЛ. 8.
НЕЛИНЕЙНЫЕ
ДИНАМИЧЕСКИЕ ПРОЦЕССЫ
Посмотрим,
выполняется ли термодинамическое условие ста-
бильности в системе (8.40). Трактуя Xi и Х
2
как концентрации
химических соединений, a k
u
k
2
, k, k' как константы скоростей,
имеем, варьируя для первой реакции Х
и
для второй реакции Х
2
причем Х° =
k
2
/k'',
Х° = ki/k. Находим
2
^~
k
'^)
(bX2)2==0
'
(8
'
49)
т. е. условие устойчивости выполнено.
Мы
исследовали поведение консервативной системы. В дей-
ствительности популяции видов
могут
расти лишь до некото-
рого предела, до значений Х\
т)
и Х
2
т
\ отвечающих насыще-
нию.
Это обстоятельство можно выразить уравнением Фер-
хулста
[107] (см. также [26, 108])
™
X)
.
(8.50)
Вводя предел размножения жертв в уравнения Вольтерра, по-
лучаем
|
(8
=
k
r
Х\Х
2
—
k
2
X
2
.
Такая
система более не является консервативной и не имеет
постоянной
движения.
Уравнения типа
(8.40)
можно обобщить на любое число взаи-
модействующих видов. Исследование соответствующих систем
очень важно для экологии (см. [26],).
То обстоятельство, что постоянная движения консервативной
системы К выражается суммой индивидуальных членов, относя-
щихся к отдельным видам, позволяет трактовать систему как
статистическую. Такая трактовка для ансамбля большого числа
§
8.3
АВТОКАТАЛИТИЧЕСКИЕ
ХИМИЧЕСКИЕ
СИСТЕМЫ
415
видов, взаимодействие которых описывается уравнениями Воль-
терра, была предложена Кернером [109].
Вернемся
к
химическим реакциям.
Рассмотрим теперь поведение системы
в
промежуточной
об-
ласти конечных,
но
больших значений полного сродства
1 <С
<
S&IRT
< оо.
Представим систему
реакций
Лотка
в
несколько изме-
ненном
виде
[1]
I
II
X
+
Y
tl
•2Y,
•
Е.
Положим
4 = 1 и для
простоты
примем
k\ =
&2
= k
3
= 1 и k-\ =
=
k-2 — ^-з = k.
Здесь
мы уже не
можем пренебречь обратными реак-
циями.
Имеем
X
= X + kX
2
— XY + kY
Y
= XY 4- kY
2
- Y -
Y\ 1
,
)
(8.52)
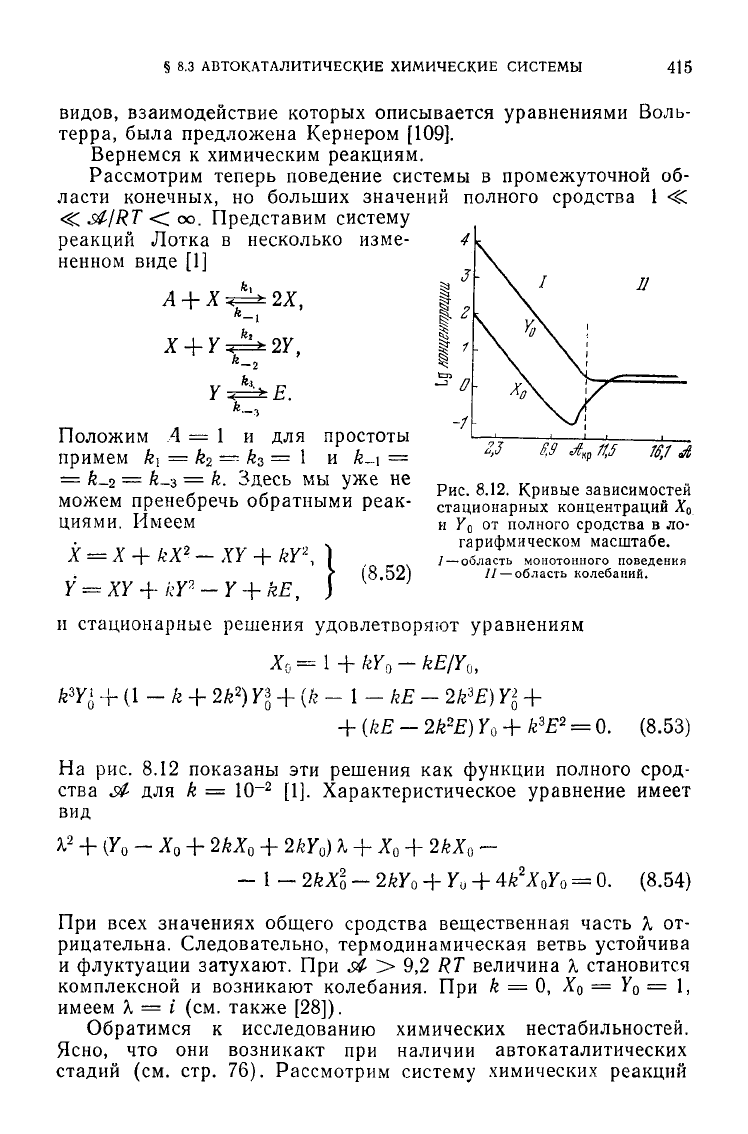
16J d
Рис.
8.12. Кривые зависимостей
стационарных концентраций ^
0
и
Y
o
от полного
сродства
в ло-
гарифмическом масштабе.
/
— область монотонного поведения
//
— область колебаний.
и
стационарные решения удовлетворяют уравнениям
Х
о
= 1 + kY
Q
-
kE/Y
0
,
k^l
f
(1
- k + 2k
2
)
Y
a
0
+
{k-l-kE
—
2k
3
E)
Y
2
0
+
+
{kE -
2k
2
E)
Y
o
+
k
3
E
2
= 0.
(8.53)
На
рис. 8.12
показаны
эти
решения
как
функции полного срод-
ства
$1>
для k = 10~
2
[1].
Характеристическое уравнение имеет
вид
2kX
0
+
2kY
0
)
%
+ Х
о
+
2kX
0
-
-
1 -
2kX
2
0
-
2kY
0
4k
2
X
0
Y
0
= 0.
(8.54)
При
всех
значениях общего сродства вещественная часть
X от-
рицательна. Следовательно, термодинамическая ветвь устойчива
и
флуктуации
затухают.
При ^ > 9,2 RT
величина
X
становится
комплексной
и
возникают колебания.
При k = 0, Х
о
= У
о
= 1,
имеем
X = i (см.
также [28]).
Обратимся
к
исследованию химических нестабильностей.
Ясно,
что они
возникакт
при
наличии автокаталитических
стадий
(см. стр. 76).
Рассмотрим систему химических реакций

416
ГЛ. 8.
НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ
несколько
более сложную,
чем
система Лотка
—
Вольтерра:
2X + YJ=±3X, (II)
B + X^D + Y, (III)
я
-з
Суммарная реакция есть
А
-\-
В
+±-
D + Е.
Условия равновесия
имеют
вид
£ fe,ft
4
£)
*
2
*з
Л
ft-,ft_
4
' В
k-
2
k-3
'
ПОЛОЖИМ
ДЛЯ простоты k\ = ki =
k%
— k\ = 1 и &_i =
=
k-
2
= fe-з =
Л_4
=
О.
Кинетические уравнения записываются
следующим образом:
(
(о.55)
У
= ВХ - X
2
Y + k (X
3
-
DY).
)
\
(
(о.
)
Стационарные
решения имеют
вид
A +
kE
(8.56)
Реакции
(I) и (IV) на
устойчивость системы
не
влияют.
По-
этому можно упростить выражения (8.56), считая,
что А и В
находятся
в
равновесии,
т. е. А =
k?E. Получаем
X
-А
у
_
Л(Л
г
+ 65) , -„
Ао
—
Т
,
У о
— —д
2 + k%B
• (Ъ.Ы)
Ищем
решения линеаризованных уравнений вблизи стационар-
ного состояния
и
находим характеристическое уравнение
(ср.
стр.
415)
Я.
2
+ [Хо + В + 1 -
2X
Q
Y
0
+ k (3Xl + D +
l)]
Я,
+
+
Jtfj
+
A;
(X§
+ D) = 0.
(8.58)
Значение
BID, при
котором коэффициент
при X
обращается
в
нуль, отвечает точке перехода.
В ней
вещественные части
кор-
ней
Х\ и Х
2
меняют знак,
и
система становится неустойчивой.
§
8.3 АВТОКАТАЛИТИЧЕСКИЕ ХИМИЧЕСКИЕ СИСТЕМЫ
417
Имеем
Я,1 + л
2
= 0, и условие перехода на основании (8.57) и
(8.58) имеет вид
(8.59)
l
Соответствующее критическое сродство равно
а
кр
= -RT\n R
Kp
k
2
.
(8.60)
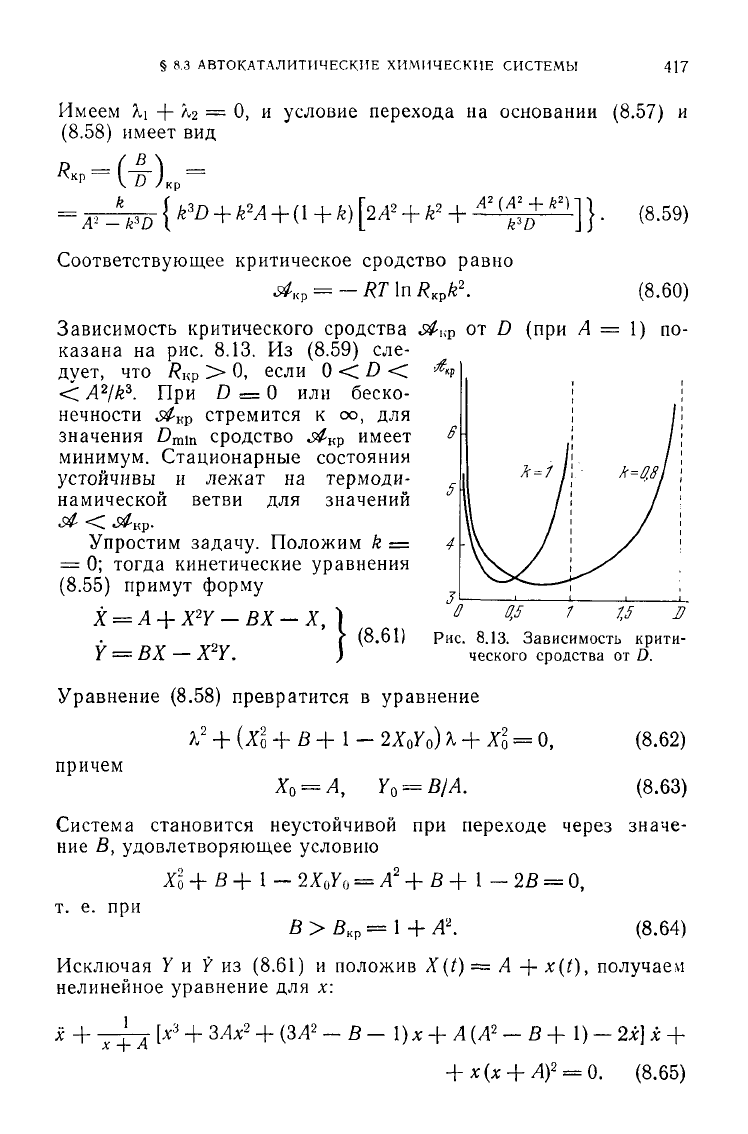
Зависимость
критического сродства «я£,
ф
от D (при /1 = 1) по-
казана
на рис. 8.13. Из (8.59) сле-
дует,
что R
Kp
> 0, если О < D <
< A
2
/k
3
. При D == 0 или беско-
нечности
j^
K
p стремится к оо, для
значения
D
mln
сродство ^
кр
имеет
минимум.
Стационарные состояния
устойчивы и лежат на термоди-
намической
ветви для значений
Упростим задачу. Положим k =
=
0; тогда кинетические уравнения
(8.55) примут форму
X = A +
X
2
Y-BX-X,
,
}
(8.61)
Y
= ВХ - Х
2
У.
Д
Рис.
8.13. Зависимость крити-
ческого сродства от D.
Уравнение (8.58) превратится
в
уравнение
Л -+- (^Ло ТОТ I —
ZAQI
о) Л т
причем
=
0,
(8.62)
(8.63)
Система становится неустойчивой при переходе через значе-
ние
В, удовлетворяющее условию
т. е. при
В + 1 -
2X
0
Y
0
= А
2
+ В+
В > В
кр
= 1 + А*.
(8.64)
Исключая
У и У из (8.61) и положив X(t) = A -f- x(t), получаем
нелинейное
уравнение для х:
ЗАх
°~
= 0. (8.65)
418
ГЛ.
8.
НЕЛИНЕЙНЫЕ
ДИНАМИЧЕСКИЕ
ПРОЦЕССЫ
Теория
показывает, что при
Л
2
— В+ 1 <0
последнее уравнение имеет периодическое решение. Но это и
есть условие неустойчивости (8.64). За точкой перехода периоди-
ческие решения всегда, находятся па конечном расстоянии от
стационарного состояния.
Точка перехода есть точка бифуркации (см. стр. 404), опи-
сываемая схемой
Устойчивый
предель-
Устойчивый
_^ Центр (в линейном приближении); S пый цикл
фокус
негрубое
образование V
4
Неустойчивый фокус.
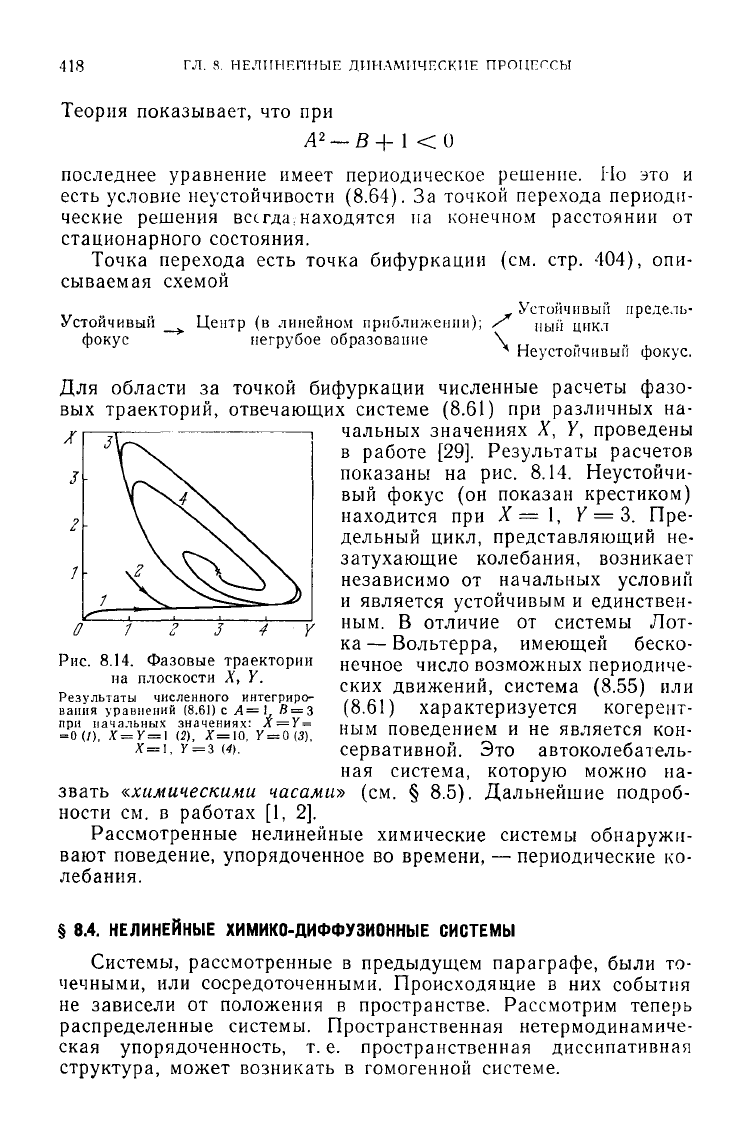
Для области за точкой бифуркации численные расчеты фазо-
вых траекторий, отвечающих системе
(8.61)
при различных на-
чальных значениях X, Y, проведены
в
работе [29]. Результаты расчетов
показаны
на рис. 8.14. Неустойчи-
вый
фокус (он показан крестиком)
находится при X = \, Y = 3. Пре-
дельный цикл, представляющий не-
затухающие колебания, возникает
независимо
от начальных условий
и
является устойчивым и единствен-
ным.
В отличие от системы Лот-
ка—
Вольтерра, имеющей беско-
нечное число возможных периодиче-
ских движений, система
(8.55)
или
(8.61)
характеризуется когерент-
ным
поведением и не является кон-
сервативной. Это автоколебатель-
ная
система, которую можно на-
звать
«химическими
часами»
(см. § 8.5). Дальнейшие подроб-
ности
см. в работах [1, 2].
Рассмотренные нелинейные химические системы обнаружи-
вают поведение, упорядоченное во времени, — периодические ко-
лебания.
Рис.
8.14. Фазовые траектории
на плоскости X, Y.
Результаты численного интегриро-
вания
уравнений
(8.61)
с А=1 В = 3
при
начальных значениях: Л=У =
=
0(7), X=Y = ] (2), *=10, У = 0(3).
Х=\,
У
=
3
(4).
§
8.4.
НЕЛИНЕЙНЫЕ
ХИМИКО-ДИФФУЗИОННЫЕ
СИСТЕМЫ
Системы, рассмотренные в предыдущем параграфе, были то-
чечными,
или сосредоточенными. Происходящие в них события
не
зависели от положения в пространстве. Рассмотрим теперь
распределенные системы. Пространственная нетермодинамиче-
ская
упорядоченность, т.е. пространственная диссипативная
структура,
может возникать в гомогенной системе.

§
8.4.
НЕЛИНЕЙНЫЕ
ХИМИКО-ДИФФУЗИОННЫЕ СИСТЕМЫ 419
Впервые проблема устойчивости по отношению к диффузии
была исследована в классической работе Тьюринга, имеющей
примечательное название «О химической основе морфогенеза»
[301.
Эта работа и исходящие из нее исследования школы При-
гожина ставят своей конечной целью дать модельное толкова-
ние
важнейших биологических явлений, определяющих онтоге-
нетическое развитие (см. гл. 9).
Дополним
уравнения
(8.61)
членами, описывающими одно-
мерную диффузию вдоль координаты г. Имеем (см. [1, 3, 115,
116, 123])
™_
= A +
X
*Y-BX-X
+ D
X
^, !
\
(8.66)
Вещества X и Y характеризуются разными константами одно-
мерной
диффузии D
x
и D
Y
. Ищем решение системы
(8.66)
в
виде концентрационных волн
У = У
о
+ 6У exp (arf +/г/Л). J
(8l67)
Здесь Л есть длина волны, характеризующая пространственную
неоднородность, ЬХ <С А'
о
, б
У
<С Уо. Получаем характеристиче-
ское уравнение
Л
2
+ (Л
2
+ l-B + a + b)X + A
2
(\ + a) + {\~B)b + ab = 0,
(8.68)
где
При
Л->оо система становится однородной и уравнение
(8.68)
совпадает с (8.62).
Уравнение
(8.68)
характеризуется двумя типами неустойчи-
вости. Первая возможность соответствует равенству нулю мно-
жителя при X и положительному значению суммы свободных
членов. Имеем условие
где
В < В
кр
,
=
1
+ А
2
+ а + Ь,
Вторая возможность соответствует равенству нулю суммы сво-
бодных членов. При этом один из корней
(8.68)
обращается
в
нуль.
420
ГЛ.
8.
НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ
Условие нестабильности имеет
вид
В > В%.
Длина волны,
при
которой
В'
кр
минимально, есть Л->оо
и
тт£к
Р
=
1 + А
2
.
Минимум
В% (Л)
имеется
при Л
2
=
(O
x
D
K
)'
/2
/.4,
он
равен
Неустойчивость возникает, когда
В
возрастает
до
меньшего
из
этих
двух
значений.
При
равенстве коэффициентов диффузии
min
Вк
Р
= 1 + А
2
< min
В%
= 1 + А
2
+ 2А
и
реализуется предельный цикл. Напротив,
при
достаточно
ма-
лых
D
X
/D
Y
происходит нарушение симметрии
и
возникает
про-
странственная неоднородность.
Для В,
немного большего
В
нр
,
I
3
X
О 0,5 1
Пространство,
произв.
вд.
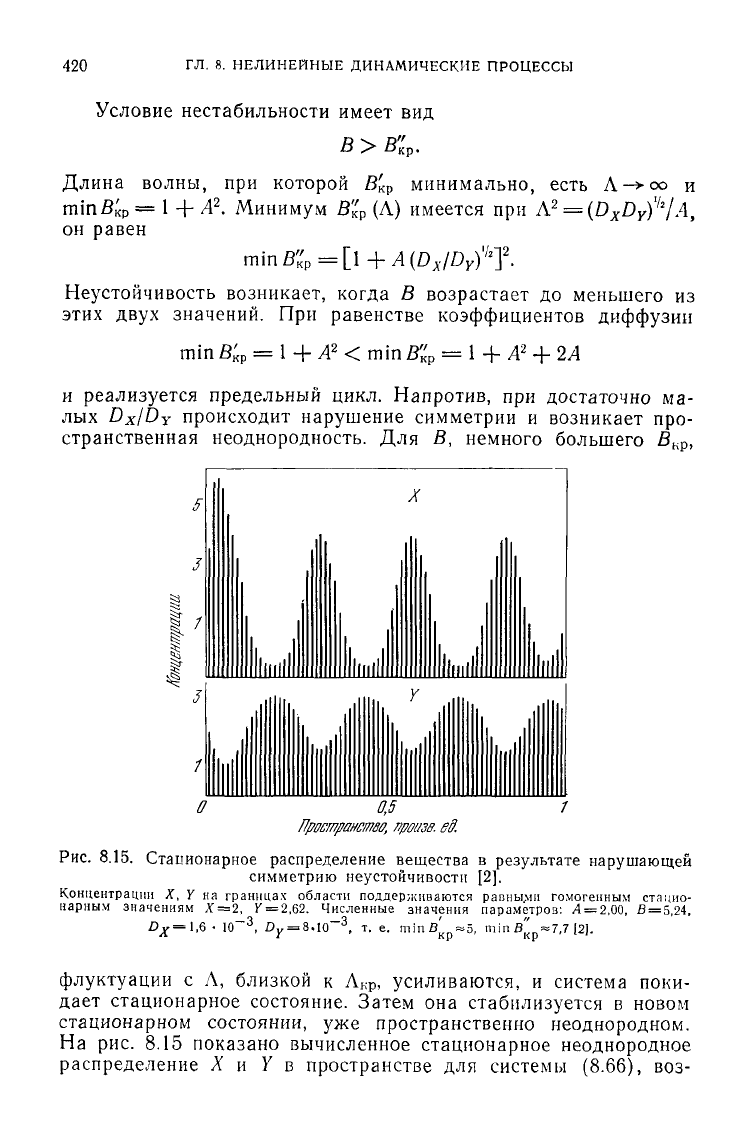
Рис.
8.15. Стационарное распределение вещества в результате нарушающей
симметрию неустойчивости [2].
Концентрации
X, Y на
границах области поддерживаются рапными гомогенным стацио-
нарным
значениям
Х =
2,
У
=
2,62. Численные значения параметров: Л
=
2,00, В
=
5,24,
D
y
= 1,6
•
"
10~
3
,
D
v
•
10
3
, т. е.
minB
Kp
=»5,
min В «7.7 12].
флуктуации
с Л,
близкой
к Л
кр
,
усиливаются,
и
система поки-
дает
стационарное состояние. Затем
она
стабилизуется
в
новом
стационарном состоянии,
уже
пространственно неоднородном.
На
рис. 8.15
показано вычисленное стационарное неоднородное
распределение
X и У в
пространстве
для
системы (8.66),
воз-
