Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

8.2.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ

ОСНОВЫ

КИНЕТИКИ

401

где

и У

—

полиномы, содержащие члены порядка выше

пер-

вого относительно

х и у.

Правые части уравнений обращаются

нуль

начале координат

х = 0, у = 0.

Следовательно

это

осо-

бая точка, отвечающая стационарному состоянию

х = у = 0.

Ограничиваясь линейным приближением,

т. е.

рассматривая

лишь

окрестность этой точки, имеем

= п\Х

-4- СЬЦ,

•

и Т

(

)

biX

+ b

y. )

Интегральная

кривая есть

bix + b

y /о io\

y '

' '

~ +

решение уравнения

(8.17)

имеет

вид

Л] exp Kit

ехр K

= В

ехр К^

+ В

ехр K

где

Я] и

—

корни характеристического уравнения

—

(Й!

-f-

) К

+ а^г —

аф\

= 0.

Это полностью соответствует изложенному выше

(в

случае

ое-

циллятора

трением было

а, = 0, а

= 1,

= —

ш^,

—2/г).

Общая классификация особых точек, данная Пуанкаре

[10], ос-

новывается

на

поведении интегральных кривых

ближайшей

окрестности этих точек.

Если

дискриминант характеристического уравнения

D =

—\a

b\—(а!

—

)

^0,

то оба

корня

К\, Я

вещественны.

Если

одновременно

аф

—

> 0, то их

знаки одинаковы.

Рас-

смотрим следующие случаи:

/. К\,

< 0.

Решение имеет

вид

убывающих экспонент,

т. е.

система, выведенная

из

особой точки,

в нее

возвращается.

Осо-

бая точка есть

устойчивый

узел.

Х\, К

> 0.

Система удаляется

от

особой точки, представ-

ляющей собой

неустойчивый

узел.

D ^ 0, но аф

—

< 0.

Корни

К\, К

имеют разные

знаки.

Особая точка является неустойчивой

именуется

седлом.

Через

нее

проходят только

две

интегральные кривые, называе-

мые сепаратрисами. Остальные фазовые траектории

уходят

бесконечность, минуя особую точку.

D < 0, но аф

—

= 0, т. е. D =

—(а,

+ b

)

, Ki = 0,

= а

. Один

из

корней равен нулю.

Для

линейной

си-

стемы

(8.17)

получается

не

особая точка,

но

прямая, соответ-

ствующая равновесным состояниям,

которую упираются

остальные интегральные прямые, направления движения

по ко-

торым зависят

от

знака

402 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Если

дискриминант D > 0, то корни %\ и

комплексно со-

пряжены.

5. Вещественные части Ки %

отрицательны, т. е.

а,\

+ Ь

< 0.

В системе происходят затухающие колебания, особая точка, на

которую накручиваются спиральные фазовые траектории, есть

устойчивый

фокус.

6. Вещественные части A,i, Х

положительны, т. е. а\ -f- Ь

> 0.

Особая точка есть

неустойчивый

фокус,

соответствующий нарас-

тающим по амплитуде колебаниям.

7. Корни h = — Х

мнимые, т. е. а

+ Ь

= 0. В системе про-

исходят незатухающие колебания, особая точка есть центр. Фа-

зовые траектории представляют собой концентрические эллипсы.

Виды особых точек, соответствующих случаям /, 3, 6, 7, по-

казаны

на рис. 8.4 [8, 11]. В рассмотренном

случае

особая точка

а)

Рис.

8.4.

Типы узловых точек

на

плоскости состояний.

а—устойчивый узел, б—седло, в—неустойчивый фокус, г—центр.

типа седла невозможна. В самом деле, условия ее появления

для осциллятора имеют вид 4/г

—

4а>1

> 0 и cog < 0, что лишено

физического

смысла при положительных значениях k и т. Осо-

бая точка типа седла имеется, например, в

случае

линейной си-

стемы, в которой

действует

сила отталкивания от положения

равновесия,

причем величина этой силы возрастает со смеще-

нием.

Так

ведет

себя, в частности, математический маятник

вблизи верхнего положения равновесия. Уравнение его движе-

ния

имеет вид

q>-f-cp =

где ф —

угол,

отсчитываемый от верхнего положения равнове-

сия,

g — ускорение свободного падения, / — длина маятника.

Перепишем

это уравнение в виде

х — пх = 0,

(8.19)

или

= у, у = пх.

(8.20)

8.2. ФИЗИКО-МАТЕМАТИЧЕСКИЕ ОСНОВЫ

КИНЕТИКИ

403

Здесь а\ = 0, аг= 1, Ь\ = п, иг = 0 и условие 3 (см. стр. 401)

соблюдается: 4я > 0, — п < 0. Уравнение

(8.21)

легко решается. Интегральные кривые отвечают уравнению се-

мейства равносторонних гипербол

с асимптотами у = — л/пх и у = ^/пх. Эти кривые показаны

на

рис. 8.5. Особая точка х = 0, у = О, находящаяся на

пересечении асимптот, является сед-

лом.

Таким

образом, особая точка изо-

бражает состояние равновесия или

стационарное состояние системы. Мы

уже говорили об устойчивых и не-

устойчивых особых точках. Определе-

ние

устойчивости состояния равнове-

сия

по Ляпунову [12] гласит (см. [8], [9],

1.2):

«состояние равновесия устойчиво,

если для любой заданной области е

допустимых отклонений от состояния

равновесия имеется область 6(е), ок-

ружающая это состояние и обладаю-

щая

тем свойством, что ни одно дви-

жение,

начинающееся внутри б, ни-

когда не достигает границы области

е.» И наоборот, состояние равновесия

неустойчиво, если имеется область е,

для которой область б

(Б)

не суще-

ствует.

Пусть на фазовой плоскости

область Б есть квадрат;

тогда

состояние равновесия х = х

у = у

устойчиво, если, задав наперед сколь угодно малое поло-

жительное значение е, можно найти такое б

(Б),

ЧТО если при

/ = 0

Рис 85

азО

вый портрет

для осциллятора с отрица-

тельным трением.

U(0)-*

|<6

ТО

ДЛЯ 0 < t < ОО

—

\<6,

Легко показать, что в рассмотренных случаях фокус и

узел

устойчивы. Гармонический осциллятор без трения совершает не-

затухающие колебания вокруг состояния равновесия, чему со-

404

ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

ответствуют

движения изображающей точки

по

концентрическим

эллипсам.

Согласно данному определению устойчивости особая

точка типа центра всегда отвечает устойчивому состоянию

рав-

новесия

[8].

Фокус отвечает неустойчивому состоянию, если трение отри-

цательно,

т. е. h <; 0.

Такая ситуация реализуется, например,

ламповом генераторе

(см. [8]). При

этом спирали

не

сверты-

ваются

фокус,

но

развертываются

из

него. Аналогичным

об-

разом,

при

большом отрицательном трении, когда

h < 0, h

> ©^, возникает неустойчивый узел. Седло отвечает неустойчи-

вому состоянию.

Теория

нелинейных динамических систем различает

«гру-

бые»

и «негрубые»

системы

[8]. В

первом

случае

малые измене-

ния

параметров системы

не

изменяют

ее

общего поведения

—

математическая модель устойчива

по

отношению

малым

из-

менениям

вида дифференциальных уравнений. Ситуации, отве-

чающие пунктам

/, 2, 3, 5, 6

приведенной выше классификации,

характеризуют

грубые

системы. Напротив,

случаях

4 и 7 си-

стемы негрубые.

самом деле,

случае

значение параметра

а\Ь

—

b\ = 0

является критическим,

при

переходе

от его по-

ложительной

отрицательной величине вместо устойчивого

узла

возникает седло.

случае

критическим является значение

па-

раметра

а\ -f- Ь

= 0 —

при переходе

{

-f- Ь

> 0

->- а\

-f- Ь

—

0 ->

П\

+ Ь

< 0

особые точки изменяют свой характер:

неустойчивый фокус —> центр

->•

устойчивый фокус.

Такие

критические значения параметра являются

бифурка-

ционными.

Проблемы теории устойчивости

методы исследования

устойчивости динамических систем подробно рассмотрены

ряде

монографий

[8,

11—18]. Краткое введение

рассматриваемую

здесь область дано

[17—19].

Из

приведенного рассмотрения линейных систем

следует

важный общий вывод. Среди

них

только гармонический осцил-

лятор

без

трения характеризуется замкнутыми фазовыми траек-

ториями,

отвечающими периодическому движению. Периодиче-

ские

процессы невозможны

для

линейных неконсервативных

си-

стем.

Обратимся теперь

нелинейным системам. Колебательное

поведение нелинейных систем весьма разнообразно

сложно.

Его изучение имеет фундаментальное значение

для

очень

ши-

рокого круга физических проблем. Физика нелинейных колеба-

ний

развита

трудах

школ Мандельштама

(см. [8,

20—22]),

Ван-дер-Поля

[23] и др.

Очевидно,

что

общие уравнения

(8.6)

нелинейны;

то же от-

носится

уравнениям (8.16), которые

мы

линеаризовали

целью

8.2. ФИЗИКО МАТЕМАТИЧЕСКИЕ ОСНОВЫ

КИНЕТИКИ

405

исследования окрестностей особых точек. Но такое исследова-

ние

не

дает

ответа на вопросы о поведении нелинейной системы

на

всей фазовой плоскости.

Нелинейная

система может характеризоваться наличием

ряда особых точек, отвечающих устойчивым и неустойчивым

состояниям. Если система консервативна, то ее уравнения дви-

жения имеют интеграл энергии

+ £/(*) = #, (8.23)

где константа интегрирования 8 зависит от начальных условий,

/2 =

тх

есть кинетическая, a U(x)—потенциальная

энер-

гии.

Движение изображающей точки зависит от соотношения

между

U(x) и &. Рассмотрим на плоскости х, z кривую г =

U(x) и прямую z = &. Возможны следующие случаи [8]:

1. Прямая z = & не пересекает кривую U(x). Если точки

кривой лежат выше точек прямой, то на фазовой плоскости нет

движения с полной энергией &'. Если прямая z = <§ лежит выше

кривой z = U(x), то на фазовой плоскости х, у имеются две

симметричные ветви фазовой траектории, по которым изо-

бражающие точки

уходят

в бесконечность (убегающие траек-

тории).

2. Прямая z = & пересекает кривую z = U(x). Для значе-

ний

х, для которых

U(x)>&,

фазовых траекторий нет, для

остальных значений х

существуют

как убегающие, так и замк-

нутые ветви, отвечающие периодическим движениям.

3. Прямая z =

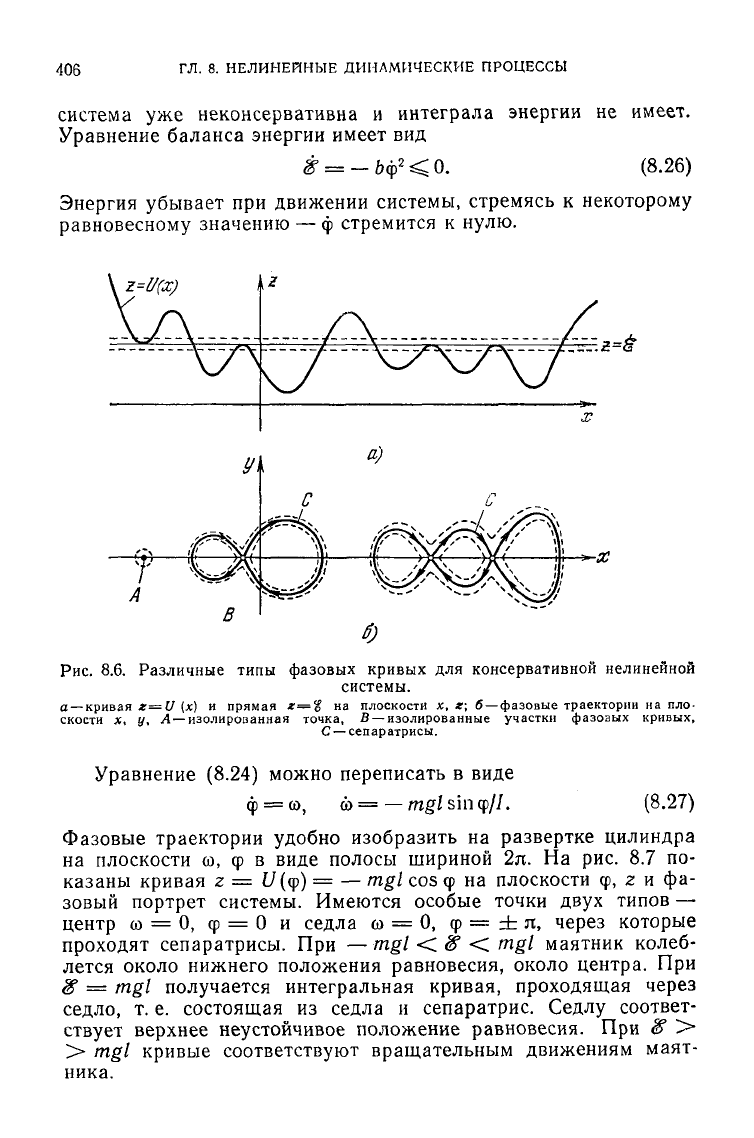
касается кривой г= U(x). Фазовые кри-

вые на плоскости х, у разбиваются на несколько классов. Воз-

можны изолированные точки, вблизи которых нет ветвей фазо-

вых кривых, отвечающие устойчивым состояниям равновесия.

Возможны изолированные конечные участки фазовых кривых —

замкнутые кривые или кривые с самопересечением. Последние

являются так называемыми сепаратрисами, т. е. кривыми, про-

ходящими через особые точки типа седла (рис. 8.6). Сепара-

трисы разделяют области, заполненные кривыми различных ти-

пов.

Поэтому нахождение сепаратрис очень важно для опреде-

ления

поведения системы. Наконец, возможны бесконечные

участки фазовых кривых. Пример нелинейной консервативной

системы — маятник, выполняющий большие колебания без тре-

ния

и описываемый уравнением движения

(8.24)

где / — момент инерции маятника. При наличии трения

/ф

&Ф

+ mgl sin ф = 0,

(8.25)

406

ГЛ.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

система

уже

неконсервативна

интеграла энергии

не

имеет.

Уравнение баланса энергии имеет

вид

= —

Ьф

< 0.

(8.26)

Энергия

убывает

при

движении системы, стремясь

некоторому

равновесному значению

— ф

стремится

нулю.

Рис.

8.6. Различные типы фазовых кривых для консервативной нелинейной

системы.

а — кривая

z=U (х) и

прямая

z=% на

плоскости

х, г;

б—фазовые траектории

на пло-

скости

х, у. Л

—изолированная точка,

— изолированные участки фазовых кривых,

—сепаратрисы.

Уравнение

(8.24)

можно переписать

виде

= — tnglsuicp/I.

со,

(8.27)

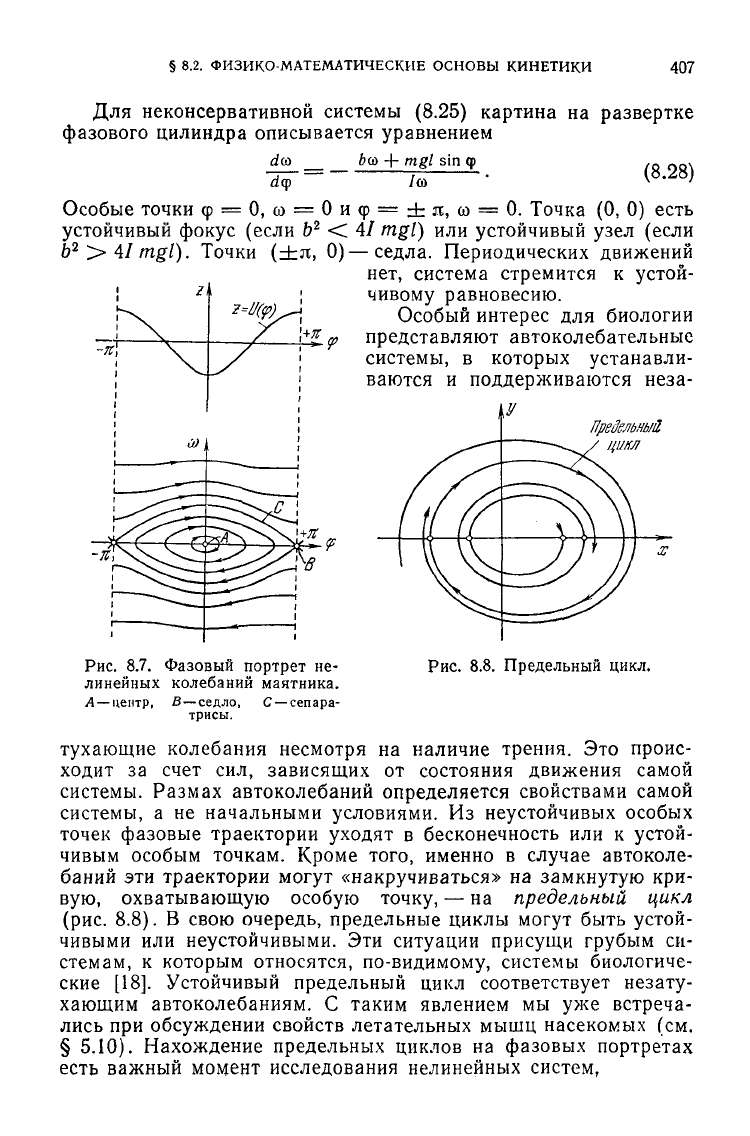
Фазовые траектории удобно изобразить

на

развертке цилиндра

на

плоскости

со, ф в

виде полосы шириной

2л. На рис. 8.7 по-

казаны

кривая

z = £/(ф) = — mgl cos ф на

плоскости

ф, z и фа-

зовый портрет системы. Имеются особые точки

двух

типов

—

центр

со = 0, ф = 0 и

седла

со = 0, ф = ± л,

через которые

проходят сепаратрисы.

При —mgl < & < mgl

маятник колеб-

лется около нижнего положения равновесия, около центра.

При

= mgl

получается интегральная кривая, проходящая через

седло,

т. е.

состоящая

из

седла

сепаратрис. Седлу соответ-

ствует

верхнее неустойчивое положение равновесия.

При

<£

mgl

кривые соответствуют вращательным движениям маят-

ника.

§ 8.2.

ФИЗИКО-МАТЕМАТИЧЕСКИЕ

ОСНОВЫ

КИНЕТИКИ

407

Для неконсервативной системы

(8.25)

картина на развертке

фазового цилиндра описывается уравнением

da> 6ш + mgl sin (p ,„ _

Особые точки ф = 0, со = Оиф = ±я, со = 0. Точка (0, 0) есть

устойчивый фокус (если Ь

< 4/ mgl) или устойчивый

узел

(если

>4/mg/). Точки (±л, 0)—седла. Периодических движений

нет, система стремится к устой-

чивому равновесию.

Особый интерес для биологии

представляют автоколебательные

системы, в которых устанавли-

ваются и поддерживаются неза-

Предельный

цикл

Рис.

8.7. Фазовый портрет не-

линейных

колебаний маятника.

А— центр, В—седло, С —сепара-

трисы.

Рис.

8.8. Предельный

цикл.

тухающие

колебания несмотря на наличие трения. Это проис-

ходит

за счет сил, зависящих от состояния движения самой

системы. Размах автоколебаний определяется свойствами самой

системы, а не начальными условиями. Из неустойчивых особых

точек фазовые траектории

уходят

в бесконечность или к устой-

чивым особым точкам. Кроме того, именно в

случае

автоколе-

баний

эти траектории

могут

«накручиваться» на замкнутую кри-

вую, охватывающую особую точку, — на

предельный

цикл

(рис.

8.8). В свою очередь, предельные циклы

могут

быть устой-

чивыми или неустойчивыми. Эти ситуации присущи грубым си-

стемам, к которым относятся, по-видимому, системы биологиче-

ские

[18]. Устойчивый предельный цикл соответствует незату-

хающим автоколебаниям. С таким явлением мы уже встреча-

лись при обсуждении свойств летательных мышц насекомых (см.

5.10).

Нахождение предельных циклов на фазовых портретах

есть важный момент исследования нелинейных систем,

408

ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ

ПРОЦЕССЫ

Классический

пример автоколебаний

—

явления, происходя-

щие

ламповом генераторе

(см. [8, 20]). В

дальнейшем изложе-

нии

рассмотрены соответствующие химические

биологические

явления.

Подробное рассмотрение нелинейных колебательных процес-

сов

применения теории

ряду

конкретных систем

—

преиму-

щественно механических

электрических

—

приведены

в [8, 11,

15—18]. Рассмотрим теперь некоторые химические системы,

ис-

следование которых оказывается связанным

биологией.

Мы

видели,

что

принципиальные

подходы

химическим системам

те

же, что и в

механике,

и в

учении

об

электричестве.

Это с осо-

бенной

ясностью демонстрируется

термодинамике сетей

(см.

стр. 79).

Особенности химических

биологических систем

состоят

следующем.

1. Динамическими переменными

химии

и в

ряде биологи-

ческих проблем являются концентрации реагентов.

На той же

основе

качестве переменных рассматриваются числа организ-

мов

(в

популяционной генетике

и в

экологии).

химико-биологической системе химические процессы

за-

частую

связаны

диффузионными,

транспортом вещества.

Иными

словами, здесь

мы

встречаемся

не с

точечными,

а с рас-

пределенными

системами.

Особое значение

для

биологии имеет

компартментализация

—

подразделение системы

на

«отсеки»,

разделенные мембранами. Система пространственно гетеро-

генна.

химических системах живой природы нелинейные хими-

ческие реакции сопряжены

как с

транспортом вещества,

так и

с механическими

электрическими процессами.

Во

многих химико-биологических процессах приходится

иметь

дело

малым числом молекул

или

макромолекул.

Как от-

мечено

в [18],

само понятие концентрации имеет здесь ограни-

ченную применимость,

и в

качестве динамических переменных

вводятся вероятности

тех или

иных состояний молекул

макро-

молекул.

В целом

химии

биологии возникает самое разнообразное

нелинейное

и, в

частности, колебательное поведение. Прямые

экспериментальные

теоретические исследования

при

помощи

простых моделей проведены пока лишь

для

немногих

случаев.

Однако полученные

результаты

очень поучительны

обещают

многое.

§ 8.3. АВТОКАТАЛИТИЧЕСКИЕ ХИМИЧЕСКИЕ СИСТЕМЫ

В биологии особое значение имеют автокаталитические

хи-

мические системы. Достаточно указать,

что

авторепродукция

клеток

организмов эквивалентна автокатализу.

8.3

АВТОКАТАЛИТИЧЕСК.ИЁ

ХИМИЧЕСКИЕ

СИСТЕМЫ

409

Вернемся сначала

феноменологическому термодинамиче-

скому рассмотрению. Как

мы

видели,

для

химических процессов

критерий

эволюции выражается условием

(ср.

(8.3))

условие устойчивости стационарного состояния имеет

вид

£ во*

b&i

(8.5)

Из

(8.29)

следует,

что

вблизи стационарного состояния

= Zbv

d{bsl

)^0.

(8.30)

Разлагая

в ряд по

6s£

получаем

*о*

££*/&*/» (8.31)

где

причем производные взяты

для

стационарного состояния.

Во-

обще говоря,

Lij

может содержать

как

симметричную,

так и

антисимметричную часть.

условиях линейности,

т. е.

вблизи

равновесия,

коэффициенты

1!ц

совпадают

коэффициентами

Онзагера

Ьц и

антисимметричные

их

части равны нулю. Вдали

от равновесия это также возможно. Тогда

= dV^0,

(8.32)

где

(8.33)

есть кинетический потенциал. Однако если антисимметричные

части

L'U

ОТЛИЧНЫ

ОТ

нуля,

то в

общем

случае

кинетический

по-

тенциал

не

существует.

Допустим,

что два

химических процесса

описываются чисто антисимметричной матрицей

Т. е.

L\\

==•

L22

= 0,

Li2

= —

Z-2i

= — L •

Тогда

(6^2

dastf-x

—

в-s^i

dbs4-

)

(8.34)

Такая

система вращается вокруг стационарного состояния,

не

попадая

него. Фазовая диаграмма имеет

вид,

показанный

на

410

ГЛ.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ

ПРОЦЕССЫ

рис.

8.9;

точка, отвечающая стационарному состоянию, есть

центр.

Вводя полярные координаты

г и ф на

плоскости s&\,

si-i,

имеем

= — L'r

dcp

< 0.

(8.35)

Но

функция

W = L'r\ не

является кинетическим потенциалом

вследствие своей многозначности

—

она возрастает

на

2nL'r

при

каждом обороте

[1].

Антисимметричность феноменологических соотношений

вы-

ражает

нелинейность.

Рассмотрим нелинейную систему химических реакций

—

мо-

дель

колебательной химической системы, впервые исследован-

ную Лотка

]24]

Y«2Y,

Y^E.

(I)

(II)

(1П)

Рис.

8.9. Обращение во- ГттпЯяпкняа

ПРЯКПИО РРТК

А ^т F Ппп-

круг стационарного

со-

лооальная реакция есть

А -_

t..

про

стояния

антисимметрич-

ecc

автокаталитическии

на

стадии

(II).

ной

химической систе- Считаем,

что

вещество

присутствует

мы

избытке,

поэтому реакция

(I)

нуле-

вого порядка.

Общее сродство, отвечающее глобальной реакции,

= a

+ s4

RT In

Вблизи равновесия система линейна:

Условие устойчивости имеет

вид

/г,

(8.36)

-ЩГ

•

(8.37)

(б^

)

> 0.

(8.38)

Вдали

от

равновесия можно пренебречь обратными реакциями,

т.

е.

положить

k-\ = fe_

= k-

— 0.

Следовательно,

s4-^>-

00. Ки-

нетические уравнения антисимметричны

-jf

= ki —

XY,

J?L

(8.39)