Волькенштейн М.В. Общая биофизика

Подождите немного. Документ загружается.

8.10. ФИБРИЛЛЯЦИЯ ВОЗБУДИМОЙ СРЕДЫ

461

что фазовый портрет системы при /

вн

= 0 характерен для воз-

будимой мембраны. Изоклина /

вн

= 0 имеет N-образную форму,

с единственной особой точкой О, под действием деполяризую-

щего тока изоклина, отвечающая ф = 0, смещается вверх.

Поведение

двух

связанных клеток описывается уравнениями

/i) + a(<Pi — ф

(8.116)

, h),

/ (ф

h) + а (ф

—

еф

2 == g (Ф2, h)-

Член

а(ф1 — фг) представляет ток /

вн

, текущий через клетку 2

от клетки 1.

Если

в момент t = 0 клетка 1 находится в состоянии, соот-

ветствующем появлению потенциала действия (ПД), то ток, те-

кущий из клетки 1 в клетку 2, может вызвать в ней ПД. На-

чальное состояние клетки 2 определяется следующим: возникает

ли

в ней ПД и через какое время после t = 0. Задержка 0 есть

время от t = 0 до возникновения ПД в клетке 2. В норме

8<т (т — длительность ПД), так как в момент t = 0 клетка 2

находится в покое. Если режим аномален, т. е. импульсы по-

даются с высокой частотой, то в момент возбуждения клетки 1

клетка 2 может оказаться в рефрактерном состоянии. В резуль-

тате

либо блокируется передача импульса от клетки 1 к клетке

2, либо ответ возникает с большой задержкой

max

~ т. Второй

случай особенно опасен для миокарда, так как при этом воз-

можно возникновение экстрасистол. Большие задержки ответа

могут

происходить в клетках, в которых постоянный ток может

вызвать автоколебания.

Таким

образом, задача о задержках сводится к изучению па-

раметров клеточной мембраны, определяющих ее поведение под

действием деполяризующего тока.

Систему уравнений

(8.116)

можно переписать в виде

еф,=/(

Фь

/,) —

<P2

= f (фг,

h = g (ф

(8.117)

где

Внешний

ток, поступающий в клетку 2, задается теперь сле-

дующим образом:

/ш.(0=-аф1(0.

(8.118)

462

ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Пусть ф]

(Л

есть прямоугольный импульс;

тогда

(8.119)

где

— аф

<р

—

амплитуда

ПД, т — его

длительность.

Имеем

систему

(8.120)

/вн(0

определяется выражением (8.119).

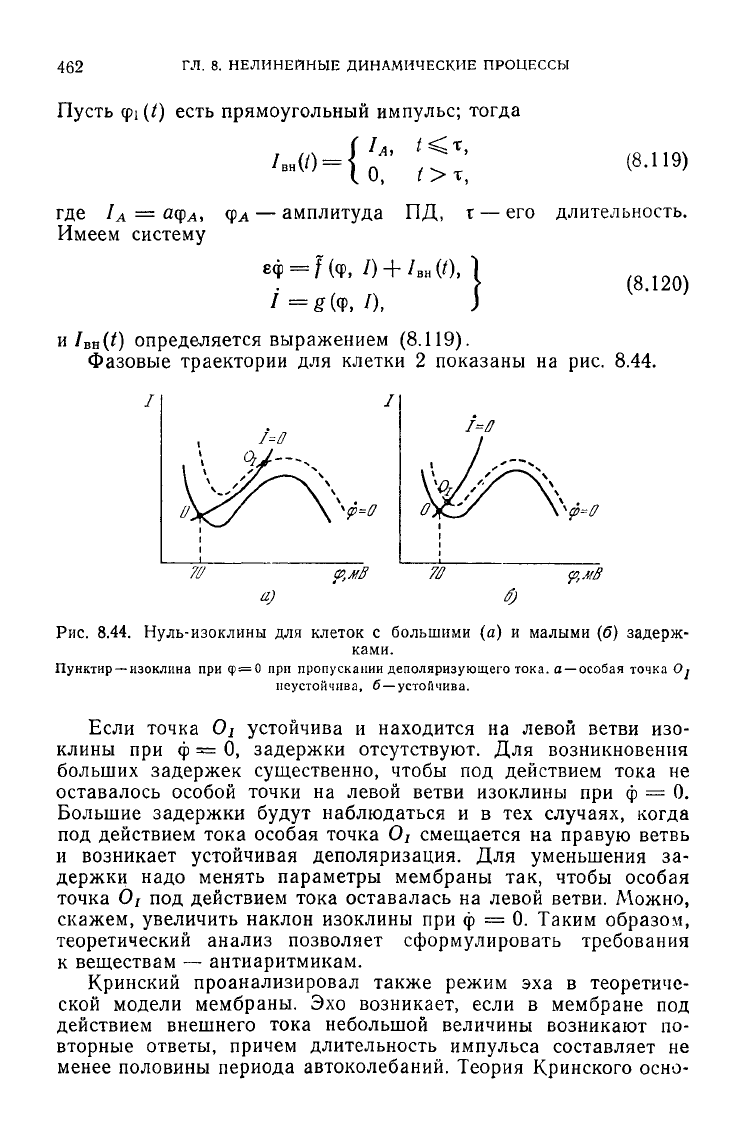
Фазовые траектории

для

клетки

показаны

на рис. 8.44.

1=0

71/

а>,мВ

а)

Рис.

8.44. Нуль-изоклины для клеток с большими (а) и малыми (б) задерж-

ками.

Пунктир

—изоклина

при

<р

= 0 при

пропускании деполяризующего тока,

—особая точка

неустойчива,

— устойчива.

Если

точка

устойчива

находится

на

левой ветви

изо-

клины

при ф = 0,

задержки

отсутствуют.

Для

возникновения

больших задержек существенно, чтобы

под

действием тока

не

оставалось особой точки

на

левой ветви изоклины

при ф = 0.

Большие

задержки

будут

наблюдаться

и в тех

случаях,

когда

под действием тока особая точка

смещается

на

правую ветвь

возникает устойчивая деполяризация.

Для

уменьшения

за-

держки надо менять параметры мембраны

так,

чтобы особая

точка

О/ под

действием тока оставалась

на

левой ветви. Можно,

скажем, увеличить наклон изоклины

при ф = 0.

Таким образом,

теоретический анализ позволяет сформулировать требования

веществам

—

антиаритмикам.

Кринский

проанализировал также режим

эха в

теоретиче-

ской

модели мембраны.

Эхо

возникает, если

мембране

под

действием внешнего тока небольшой величины возникают

по-

вторные ответы, причем длительность импульса составляет

не

менее половины периода автоколебаний. Теория Кринского осно-

5 8.11.

НЕЛИНЕЙНОСТЬ

РЕГУЛЯЦИЯ

463

вана на широком применении

метода

фазовых портретов, отве-

чающих модельным уравнениям, описывающим мембранные

системы.

Теория

фибрилляции сердечной мышцы, исходящая из общих

положений

физики нелинейных колебательных систем, является

прекрасным

примером биофизического исследования, доведен-

ного до важных практических приложений. Задачи физиологии

четко сформулированы здесь как физические проблемы. Это

краткое изложение показывает, что именно физический

подход

физиологии обеспечивает строгость и общность анализа и под-

линное

обоснование получаемых выводов.

8.11.

НЕЛИНЕЙНОСТЬ И РЕГУЛЯЦИЯ

Биологические макромолекулы, надмолекулярные

структуры,

органоиды клетки, клетки, организмы представляют собой слож-

ные

системы, т. е. совокупности элементов, взаимодействующих

друг

другом.

Изучение явлений жизни

исходит

из исследования

этих взаимодействий.

Вместе

с тем физическое рассмотрение

сложной системы не может не основываться на изучении состав-

ляющих ее элементов, взятых порознь, вплоть до молекулярного

уровня структурно-функциональной организации. Сами взаимо-

действия определяются природой этих элементов. Соответствен-

но

мы имеем

дело

с ферментом и геном, с аксоном и миофибрил-

лой,

с митохондрией и хлоропластом. Эти элементы более слож-

ных систем в свою очередь представляют собой сложные си-

стемы. Анализ явлений жизни на

всех

уровнях организации

требует

подходов, коррелирующих с представлениями общей

теории систем [101].

Специфические

взаимодействия в биологической системе при-

водят к регуляции ее поведения, к поддержанию постоянных

значений

жизненно важных параметров у системы, достигшей

взрослого состояния, и к направленной самоорганизации разви-

вающегося организма. В биологии давно фигурирует понятие

гомеостаза, означающего стационарное состояние внутренней

среды. Холдспн писал:

«Активное

поддержание нормальной и

притом специфической

структуры

и есть то, что мы называем

жизнью;

понять сущность этого процесса — значит понять, что

такое жизнь» [102]. Однако, как указал Уоддингтон

[10Э},

поня-

тие гомеостаза недостаточно. Жизненные явления имеют дина-

мический

характер, и существенна не стабилизация состояния,

а стабилизация потоков. Соответственно, Уоддингтон вводит по-

нятие

гомеореза,

означающего наличие стационарного состояния

или

стационарной замкнутой траектории на фазовом портрете

открытой системы. Гомеорез поддерживается регуляционными

процессами,

восстанавливающими фазовые траектории при от-

464 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

клонениях

от них, вызванных изменениями условий. Гомеорети-

ческая система — открытая система, взаимодействующая со

своим окружением.

Пользуясь языком теории регулирования [104, 105], скажем,

что открытая система характеризуется наличием входного и вы-

ходного сигналов. Эти понятия означают воздействие на систему

ее ответную реакцию. Закон поведения системы определяет

зависимость выходной величины от входного воздействия, или

сигнала. Задачи теории систем в их общей формулировке со-

стоят в комбинировании

двух

известных факторов с целью на-

хождения третьего [104]. Эти три фактора — входная величина,

закон

поведения, выходная величина. Основные проблемы био-

физики

сводятся к нахождению структуры и законов поведения

«черного ящика», т. е. биологической системы. «Черными ящи-

ками» являются и фермент, и клетка, и организм. Инженер кон-

струирует

и строит «белый ящик» — машину, преобразующую

входные сигналы в выходные в соответствии с поставленной

целью. В биологии «ящики» созданы природой, а не инженером,

задача физика состоит в исследовании их внутреннего устрой-

ства и функциональности.

Регуляция, обеспечивающая поддержание гомеореза или оп-

тимальной для жизни реакции на внешние воздействия [106],

осуществляется в

результате

взаимодействия

между

входным и

выходным сигналами, т. е. вследствие обратной связи. В простей-

шем

случае

регуляция поддерживает выходную величину на по-

стоянном

уровне — скажем, температуру лабораторного термо-

стата. Простейшая регулируемая система содержит управляю-

щее устройство, подвергающееся воздействию выходного сигнала,

объект управления, выдающий этот сигнал (см. стр. 374).

Взаимодействия в биологической системе осуществляются

сильными

— химическими и слабыми — межмолекулярными и

другими силами (см. стр. 9). Как правило, химические реак-

ции

нелинейны. Нелинейны и слабые взаимодействия, имеющие

кооперативный

характер. Кооперативность всегда означает не-

линейность

ответа системы на входной сигнал.

Как

показано выше, нелинейные системы

ведут

себя весьма

специфически

и разнообразно. Наличие множественных стацио-

нарных состояний — устойчивых и неустойчивых — определяет

возможности переключения системы из одного режима в

другой

даже

при слабых воздействиях. Таким образом, нелинейные

системы обладают особыми регуляторными возможностями.

Математический аппарат теории управляющих систем есть

аппарат дифференциальных уравнений. Связь

между

выходными

y(t)

и входными f(t) сигналами задается дифференциальным

уравнением. Метод передаточных функций, основанный на при-

менении

преобрязования Лапласа (см. [106]), позволяет полу-

8.12.

ДИНАМИЧЕСКИЕ

ПРОЦЕССЫ

ФАЗОВЫЕ

ПЕРЕХОДЫ

465

чить простое феноменологическое описание систем управления.

Однако линейное приближение

ряде случаев оказывается

слишком

грубым

и не

передает основные особенности системы.

При

исследовании нелинейных

(в

частности, кооперативных)

систем особенно эффективен неоднократно примененный

этой

главе метод фазовых портретов, позволяющий непосредственно

анализировать проблемы устойчивости.

Рассмотрение организма

как

регулируемой системы, прово-

димое физико-математическими методами, представляет собой

основу теоретической физиологии.

В § 8.10

изложены представ-

ления,

относящиеся

проблемам физиологии сердечной мышцы.

Реверберационная

теория фибрилляции рассматривает наруше-

ние

регуляторного режима, приводящее

десинхронизации

ав-

токолебаний

распределенной нелинейной системе. Теория

по-

зволяет установить параметры,

от

которых зависит поведение

системы,

указать способы воздействия

на эти

параметры.

В сущности, такой

же

характер имеет целый

ряд

фундаменталь-

ных физиологических проблем. Необходимо раскрыть физиче-

скую сущность регуляционных явлений, установить,

от

чего

за-

висит регуляция,

и, тем

самым, найти причины патологических

отклонений.

Физика есть основа физиологии.

8.12. НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

ФАЗОВЫЕ ПЕРЕХОДЫ

Нелинейные

системы характеризуются фазовыми портретами

с различными особенностями,

частности,

устойчивыми

и не-

устойчивыми особыми точками. Нелинейные системы способны

переходить

из

одних состояний

другие

под

действием малых

флуктуации, нарастающих

до

макроскопического уровня.

Шлёгль впервые показал,

что в

ряде случаев поведение

не-

линейной

системы оказывается подобным

фазовому

переходу

первого

или

второго рода [117]. Возникновение новой структуры

распределенной нелинейной системе имеет такой характер.

Неравновесные

переходы, определяемые неустойчивостями,

дав-

но

известны

гидродинамике (например, переход

от

ламинар-

ного

турбулентному течению

эффект Бенара,

см. [1, 115,

116]).

Рассмотрим вслед

за

Шлёглем

[117, 118]

автокаталитические

реакции

(ср. стр. 415)

+ 2Х ^ ЗХ, В+Х ^ С.

*-1

*-2

Скорости

реакций равны

— k-

и nv un \

(8.121)

— k-

C. )

v ;

466

ГЛ.

НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Положим

для простоты fc_i = 1, k\A = 3 и обозначим k

B = р,

C = у- Скорость изменения концентрации X равна

у __, _, „. __ v3 I О у2 о у I ^ /о

ОО\

Стационарные

состояния отвечают условию X = 0 или

Y = X

- ЗХ

+ Р*.

(8.123)

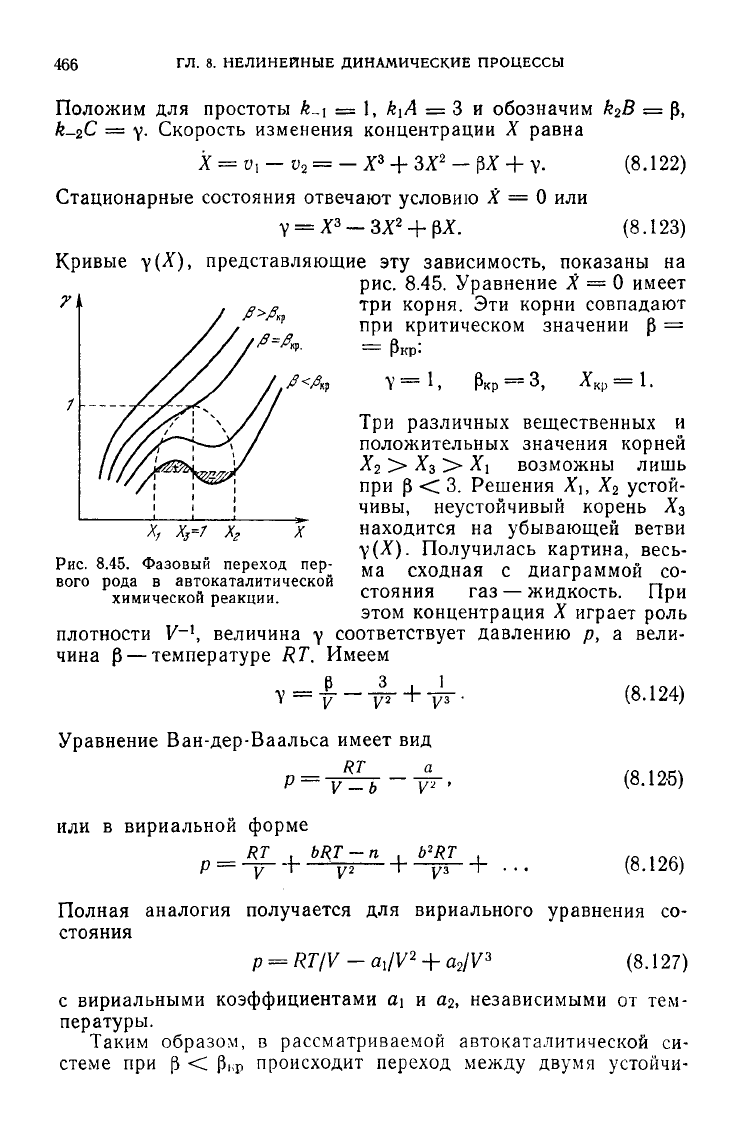
Кривые

Y№> представляющие эту зависимость, показаны на

рис.

8.45. Уравнение X = 0 имеет

три корня. Эти корни совпадают

при

критическом значении р =

/>А

Y=l,

== 3,

кр

=1.

}

Рис.

8.45. Фазовый переход пер-

вого

рода в автокаталитической

химической

реакции.

Три

различных вещественных и

положительных значения корней

> -^3 > ^1 ВОЗМОЖНЫ

ЛИШЬ

при

р < 3. Решения Х

устой-

чивы,

неустойчивый корень Х

находится на убывающей ветви

V(^). Получилась картина, весь-

ма сходная с диаграммой со-

стояния

газ — жидкость. При

этом концентрация X играет роль

р р р

плотности V-

, величина у соответствует давлению р, а вели-

чина

р — температуре RT. Имеем

В_ 3 1

У у у2 I yi •

Уравнение Ван-дер-Ваальса имеет вид

RT а_

Р V — b V

или

в вириальной форме

Е1

. bRT-n . b

RT .

= -IT

Г —уз- +

• •

•

(8.124)

(8.126)

Полная

аналогия получается для вириального уравнения со-

стояния

(8.127)

р = RT/V -

с вириальными коэффициентами а\ и а

2у

независимыми от тем-

пературы.

Таким

образом, в рассматриваемой автокаталитической си-

стеме при р < р,

происходит переход

между

двумя устойчи-

8.12. ДИНАМИЧЕСКИЕ ПРОЦЕССЫ И ФАЗОВЫЕ ПЕРЕХОДЫ

467

выми стационарными состояниями Х

и Х

, подобный фазовому

переходу первого рода. Внешним условиям, задаваемым р и у.

отвечают два конкурирующих состояния Х

и Х

. Этот переход

не связан с нарушением симметрии. Можно показать, что усло-

вие Максвелла — равенство площадей + и — на рис. 8.45 — со-

блюдается.

Если одновременно с химической реакцией происходит диф-

фузия компонента X (система является распределенной), то при

постоянных значениях А, В, С получаем

(8.128)

(8.129)

причем у(Х) можно представить в виде

Y (X) = 4г

(*) = 7Д

~ *

•

Ф{Х) играет роль некоторого потенциала. Считая диффузию од-

номерной,

перепишем уравнение

(8.128)

в виде

-£>S-

(8-130)

(8.131)

Стационарные состояния удовлетворяют уравнению

__ дФ (X)

~ дХ '

Это уравнение сходно с уравнением, описывающим движение

массы в потенциальном поле, если

z играет роль времени, а X — коор-

динаты. Имеется стационарное со-

стояние,

в котором сосуществуют

две фазы Х

, Х

, причем

Х—*-Х\

при

z-+oo

и X -> Х

при z-> — оо. Х

соответствуют относительные

максимумы Ф(Х). В стационарном

состоянии происходит перемещение

«массы»

D от одного максимума

Ф(Х), при котором эта масса по-

коилась, к

другому

максимуму, в

котором она также достигает со-

стояния

покоя. Это возможно лишь в том случае, когда значе-

ния

Ф в обеих точках одинаковы (рис.

8.46):

(8.132)

Рис. 8.46.

Сосуществование

фаз

^i и Xi.

Мы

получили условие сосуществования

двух

фаз, которое

фиксирует значение у. Как показывает Шлёгль, из условия

(8.132)

следует

Y = p-2,

112

=1=р(3-р)'\

*з=1.

(8-133)

468

ГЛ.

НЕЛИНЕЙНЫЕ ДИНАМИЧЕСКИЕ ПРОЦЕССЫ

Наряду с фазовыми переходами первого рода нелинейные

автокаталитические процессы

могут

приводить к неравновесным

переходам, подобным фазовым переходам второго рода. Рас-

смотрим реакции

— 1

— 2

BX-k-

(8.134)

Р, k-

C = y. Находим

(8.135)

Их

скорости равны

AX—k-

Положим

/г

Л==1,

/г_, = 1,

X > 0 при малых I и 1<0 при больших X. Следовательно,

стационарное состояние, отвечающее X = О, устойчиво. В этом

состоянии

—Л

—(1—p)

Л =—

/(•<*.)•

(о. loo)

Если у = 0.

т0

— Р при р< 1,

(8.137)

•Ч

0 при р> 1.

Такое поведение величины X характерно для фазового перехода

второго рода, скажем, перехода из ферромагнитного в парамаг-

нитное состояние. В этой аналогии X играет роль параметра

упорядоченности (намагниченности), у — напряженности маг-

нитного поля, р — температуры.

Значение р = р

р = 1 отвечает точ-

ке Кюри. При р < р

кр

происходит

нарушение симметрии. В критиче-

ской

точке малые флуктуации воз-

растают до макроскопических зна-

чений.

Имеем, согласно (8.135),

отсюда

Рис.

8.47. Фазовый переход

второго рода в автокаталити-

ческой химической реакции.

или

(8.138)

(8.139)

где т-

= 2Х — (1— Р). При Y-^0 *->0 и

тг—

—*11 — р|. Но

отсюда

следует,

что в критической точке р = р

кр

= 1, т-»оо.

На

рис. 8.47 показаны кривые зависимости X от р при раз-

личных значениях Y-

Эти аналогии, найденные Шлёглем, весьма поучительны. По-

ведение модельной химической системы, подобное фазовому пе-

8.12. ДИНАМИЧЕСКИЕ ПРОЦЕССЫ И ФАЗОВЫЕ ПЕРЕХОДЫ 469

реходу,

свидетельствует о ее кооперативных свойствах в истин-

ном

смысле этого слова, о переходах типа

«все

или ничего». Как

мы видим, модели биологических систем, описывающие самоор-

ганизацию,

имеют именно такой характер. Это —

триггерные

системы, совершающие переходы в

результате

малых флуктуа-

ции.

Соответственно можно

думать,

что идея о неравновесных

фазовых переходах как механизме биологических явлений яв-

ляется многообещающей. Уже получены некоторые интересные

результаты. В работе [119] исследованы неравновесные фазовые

переходы в системах ферментативных реакций при наличии суб-

стратного ингибирования и диффузии. Показана возможность

пространственного разделения фаз, соответствующих комплек-

сам фермента с несколькими молекулами субстрата. Есть осно-

вания

думать,

что эти же представления окажутся весьма важ-

ными

для понимания функционирования биологических регуля-

торных систем, в частности мембранных.

Как

мы уже не раз подчеркивали, имеется далеко идущее

сходство

между

химическими открытыми системами и системами

экологическими

— соответствие

между

моделями Лотка и Воль-

терра (см. стр. 411). Посмотрим, каким образом аналогия с фа-

зовыми переходами проявляется в моделях эволюционирующих

популяций

[120].

Рассмотрим менделевскую диаллельную популяцию диплоид-

ных организмов с полным скрещиванием.

Аллель

а отвечает дикому типу, Ь — мутантному. Можно оп-

ределить коэффициенты приспособленности генотипов аа, ab, bb,

равные соответственно w\, до

, w

, как удельные скорости роста

численности соответствующей популяции

Пусть частота прямых мутаций

а —• й на

поколение равна

ц,

частота обратных мутаций

b —*• а

равна

v. Как

показывает дина-

мическая

теория популяций

(ср. [121,

122]), динамика частоты

появления

гена

описывается уравнением

dt—PV

Р) ^р* +

2а,

2Р

(1 - р) + и,

(1 -

Р)

1*Р

И-

-v

С1

Р)-

(8.141)

Здесь время измеряется

числе поколений.

При

выводе урав-

нения

(8.141)

предполагалось,

что |i,v€ 1; w\ — ш

, w

— w

до

. В

этом

случае

вид

формулы

не

зависит

от

того,

что

чему

предшествует,

—

мутация отбору

или

наоборот. Перепишем

уравнение

(8.141)

виде

|f = R-

]

(р) (а

- а,р -

(8.142)

470 ГЛ. 8.

НЕЛИНЕЙНЫЕ

ДИНАМИЧЕСКИЕ

ПРОЦЕССЫ

где

2ш

р(1 _ р) + о,

(1 _

)2 > о, (8.143)

a, = цш1 —и, a

= x(3<7

= x(l—2q)/q,

= w

— w

Величина q выражает степень доминирования аллели а в гете-

розиготе ab, т. е. 0 < q = (w

—

)/(wi

— w

) < 1. Выражения

коэффициентов

а,- (см.

(8.144))

получаются при условиях р < w

ц,

v < 1, v < ц.

В стационарном состоянии популяции р = const, и из

(8.142)

находим для стационарных значений р

(8.144а)

Изменению

условий существования популяции отвечает из-

менение

параметров р\ ц, v, определяющих, согласно (8.142),

темп эволюции и, согласно (8.144а), ее конечный

результат.

Диа-

грамма стационарных состояний — зависимость / от р

(8.144а)

—

совершенно подобна зависимости (8.123), представленной

рис.

8.45. Эти «ван-дер-ваальсовы» кривые получаются при раз-

личных значениях х при условиях х <С \iw\ {а\ > 0) и q <

/з

(о&2 < 0, а

>0). При этом кубическое уравнение

(8.144а)

имеет три вещественных положительных

корня,

совпадающих

критической точке, в которой

и одновременно

9(1

-2<?)(1

-3

+ 3

) '

При

х > х

кр

существуют

три стационарных значения pi <

< рз < р2, причем рз — неустойчиво, а рь р

— устойчивы. По-

добно реальному

газу

популяция способна пребывать в

двух

устойчивых стационарных состояниях, переход из одного состоя-

ния

другое

аналогичен фазовому

переходу

первого рода. Пе-

реход

вызывается достаточно большими флуктуациями числен-

ности

и состава популяции.

Допустим, что популяция непрерывно расселена в своем

ареале. Динамика популяции описывается уравнением, вклю-

чающим миграцию особей (диффузию)

4>(p)

£V

(8.147)

где \|з(р)—правая часть уравнения (8.142), а коэффициент диф-

фузии D выражается через среднее расстояние г, на которое

мигрируют особи за время жизни х, D = г

/т. Диффузия не на-