Baker R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications

Подождите немного. Документ загружается.

10.1

INTRODUCTION

217

Profile

Figure

10.2.

Velocity profiles

inlet

to, and in the

annulus

of, a

turbine

meter.

which provides the basis for the constant, which in various units and dimensions

is known as meter registration, meter constant, meter coefficient, calibration factor,

etc.,

and is measured in pulses per unit volume or radians per unit volume. We shall

call this the K factor, in (pulses per cubic meter), as in Chapter 1.

Tan

(1973;

cf. Fakouhi 1977) gives an equation of the form

-*- = a

(10.4)

where the second term is affected by the viscosity and leakage, and the third term

is affected by the mechanical and aerodynamic drag. Adjusting these two terms has

been found to affect the familiar hump in the turbine characteristic (cf. Newcombe

et al. 1972 who gave an equivalent equation for gas meters).

However the theory is not, unfortunately, as simple as this because the blades do

not cut the fluid perfectly, and the value of r and

must change to accommodate

the profile across the pipe.

Suppose that we consider the variation of blade angle for a uniform profile A

(Figure 10.2), then it can be seen that, with no variation in axial velocity across the

annulus, the correct blade angles will be given by

tan/3/r = constant

(10.5)

If the midspan blade angle is 41° as in Xu's papers (1992a, 1992b) then the

values at hub and tip will be 30° and 49° as in Xu's meter, suggesting that this was

the method applied in the design which he used. If, however, profile

existed, then

the flow will not meet the blades at the correct angle, and the designer may adjust

the blade twist to allow for this. The reader is also referred to Hochreiter's (1958)

paper where he allows for blade obstruction.

It thus becomes apparent why the flowmeter will be susceptible to incorrect

installation, since this will cause a flow profile that results in the wrong incidence

angle for some parts of the annulus. It also suggests why a turbine wheel, which is

optimized for flow profile range, will give a better performance than one with, say,

constant angle blades. To develop a fuller theory, it is necessary to take account of

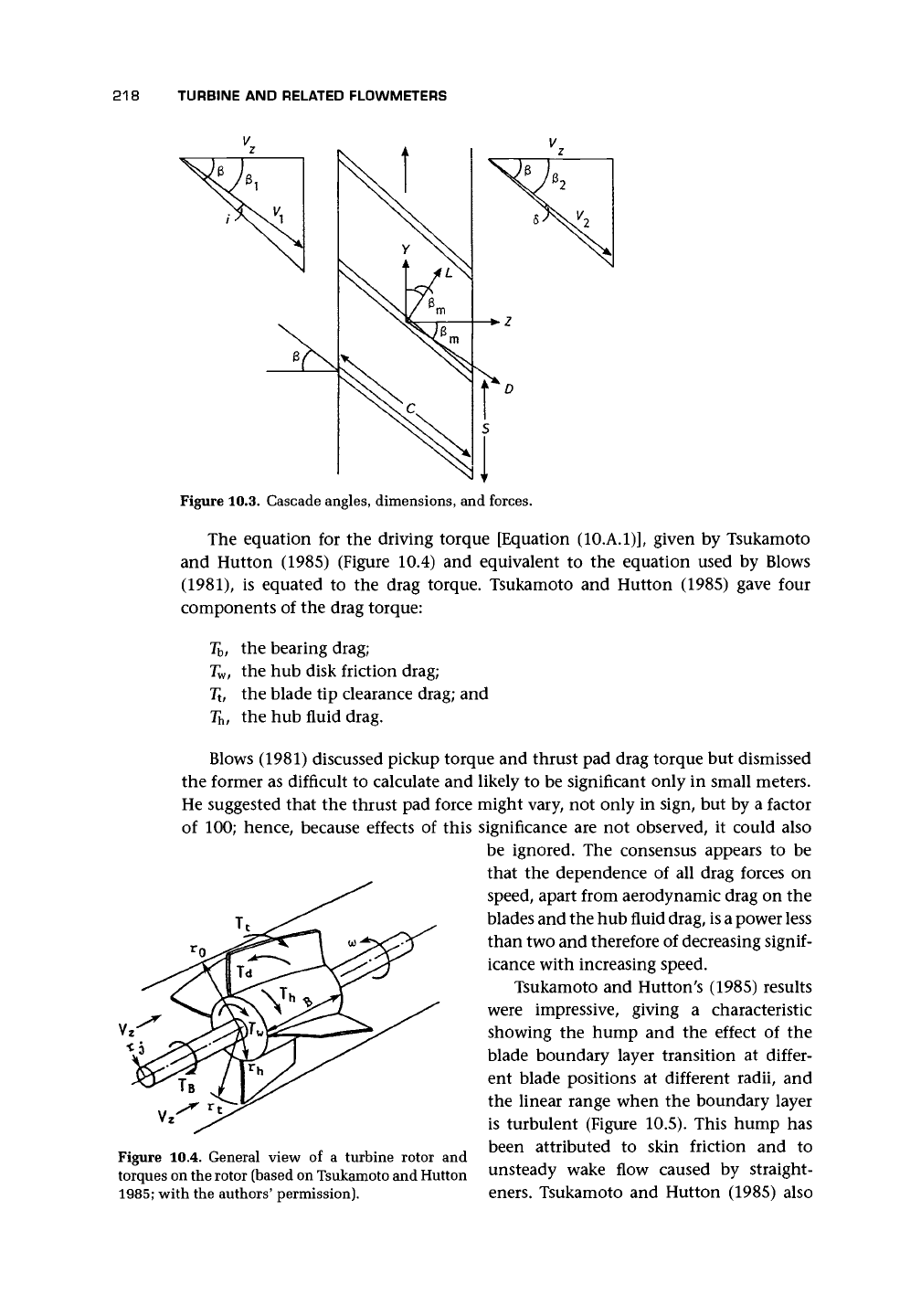
the lift and drag on the blades, bearings, etc. Figure 10.3 sets out the main angles

and forces for a cascade of blades. The analysis is given in Appendix

10.A.1.

Tsukamoto and Hutton (1985) predicted the complete characteristic of a turbine

meter with reasonable accuracy allowing for viscosity, inlet flow profile, and meter

geometry. Blows (1981) developed a model of a turbine flowmeter, which allowed

the effects of viscosity and tip clearance to be examined.

218

TURBINE

AND

RELATED FLOW METERS

Figure

10.3.

Cascade

angles,

dimensions,

and

forces.

The equation for the driving torque [Equation (10.A.1)], given by Tsukamoto

and Hutton (1985) (Figure 10.4) and equivalent to the equation used by Blows

(1981),

is equated to the drag torque. Tsukamoto and Hutton (1985) gave four

components of the drag torque:

, the bearing drag;

the hub

disk friction drag;

the

blade

tip

clearance drag;

and

the hub

fluid drag.

Blows (1981) discussed pickup torque

and

thrust

pad

drag torque

but

dismissed

the former

difficult

calculate

and

likely

to be

significant only

small meters.

He suggested that

the

thrust

pad

force might vary,

not

only

sign,

but by a

factor

100;

hence, because effects

this significance

are not

observed,

could also

be ignored.

The

consensus appears

to be

that

the

dependence

of all

drag forces

speed, apart from aerodynamic drag

on the

blades

and the hub

fluid drag,

is a

power less

than

two and

therefore

decreasing

signif-

icance with increasing speed.

Tsukamoto

and

Hutton's (1985) results

were impressive, giving

characteristic

showing

the

hump

and the

effect

of the

blade boundary layer transition

differ-

ent blade positions

different radii,

and

the linear range when

the

boundary layer

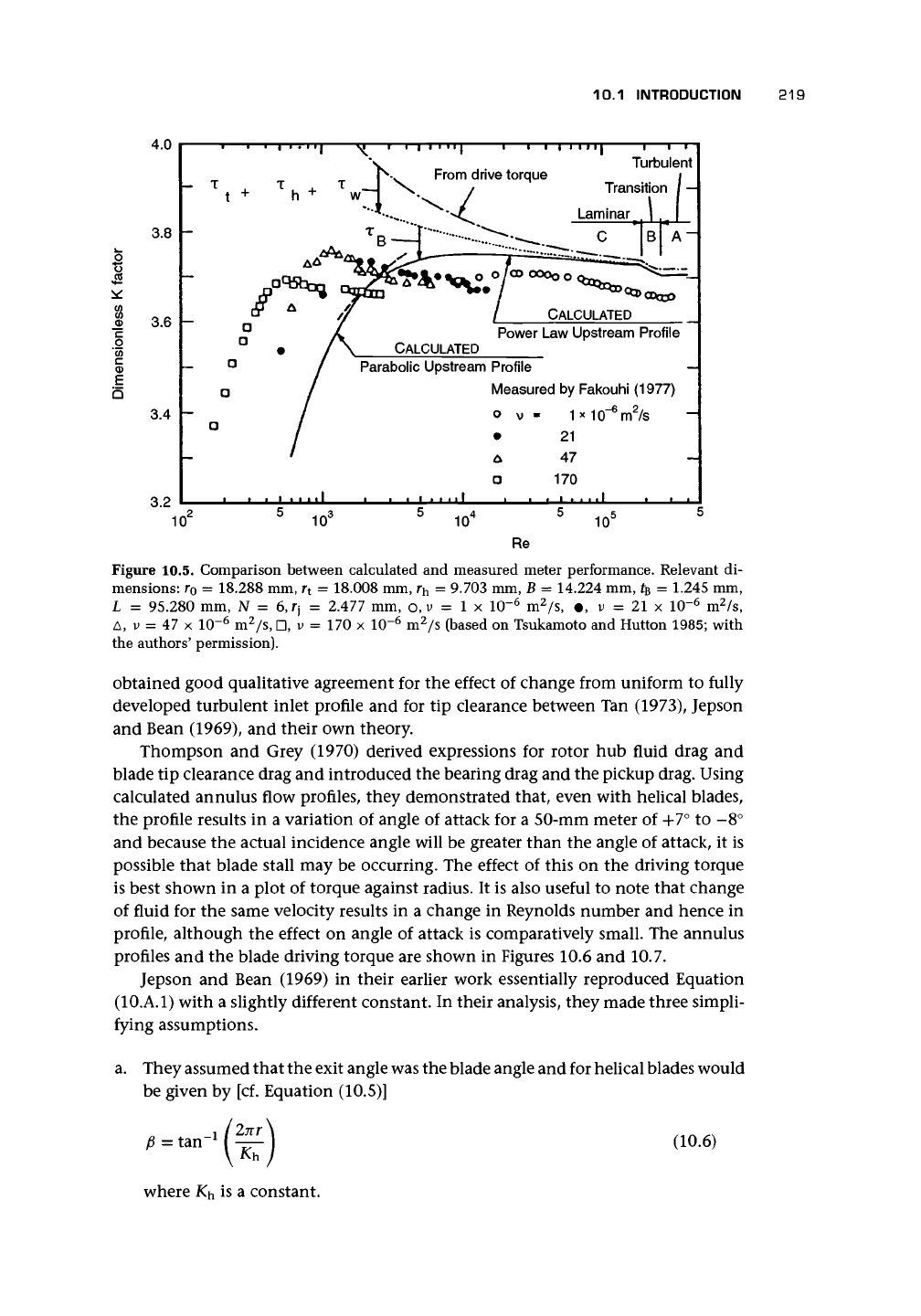
is turbulent (Figure 10.5). This hump

has

been attributed

skin friction

and to

Figure

10.4.

General view

of a

turbine rotor

and

torques on the rotor (based on Tsukamoto and Hutton unsteady wake flow caused by straight-

1985;

with the authors' permission). eners. Tsukamoto and Hutton (1985) also

10.1 INTRODUCTION

219

Turbulent

Transition /

—

Laminar . 1

3.4

3.2

Power Law Upstream Profile

1*10~

Parabolic Upstream Profile

Measured by Fakouhi (1977)

o v »

• 21

A 47

a 170

, , , , • • .,! . ..... ..I I

10°

10*

10°

Figure 10.5. Comparison between calculated and measured meter performance. Relevant di-

mensions: r

= 18.288 mm, r

= 18.008 mm, r

= 9.703 mm, B = 14.224 mm, t

= 1-245 mm,

L = 95.280 mm, N = 6,fj = 2.477 mm, o, v = 1 x 10"

/s, •. v = 21 x 10~

/s,

A, v = 47 x 10~

/s, D, v = 170 x 10~

/s (based on Tsukamoto and Hutton 1985; with

the authors' permission).

obtained good qualitative agreement for the effect of change from uniform to fully

developed turbulent inlet profile and for tip clearance between Tan (1973), Jepson

and Bean (1969), and their own theory.

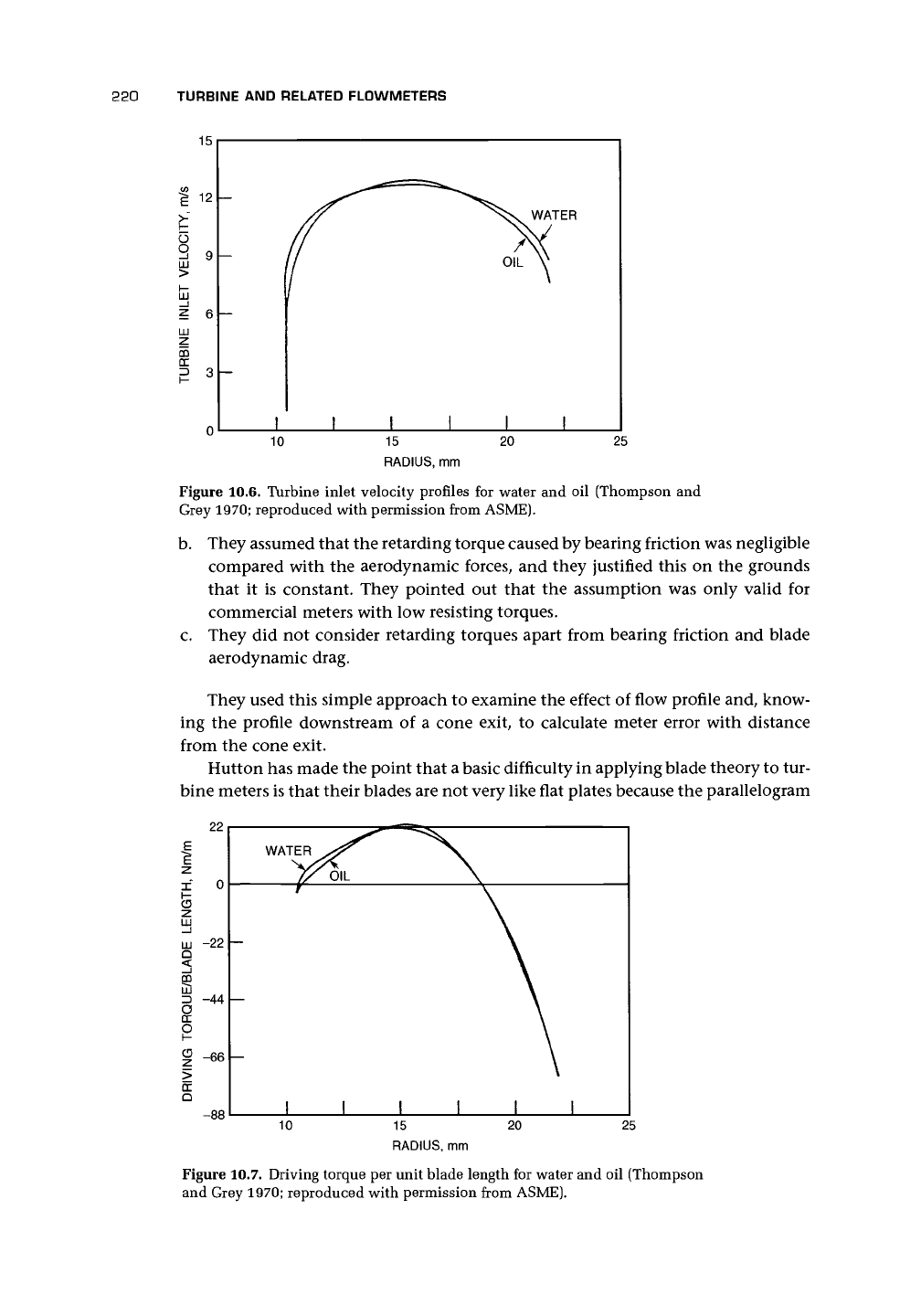
Thompson and Grey (1970) derived expressions for rotor hub fluid drag and

blade tip clearance drag and introduced the bearing drag and the pickup drag. Using

calculated annulus flow profiles, they demonstrated that, even with helical blades,

the profile results in a variation of angle of attack for a 50-mm meter of +7° to -8°

and because the actual incidence angle will be greater than the angle of attack, it is

possible that blade stall may be occurring. The effect of this on the driving torque

is best shown in a plot of torque against radius. It is also useful to note that change

of fluid for the same velocity results in a change in Reynolds number and hence in

profile, although the effect on angle of attack is comparatively small. The annulus

profiles and the blade driving torque are shown in Figures 10.6 and 10.7.

Jepson and Bean (1969) in their earlier work essentially reproduced Equation

(10.A.1) with a slightly different constant. In their analysis, they made three simpli-

fying assumptions.

a. They assumed that the exit angle was the blade angle and for helical blades would

be given by [cf. Equation (10.5)]

= tan"

2nr\

(10.6)

where K

is a constant.

220 TURBINE AND RELATED FLOWMETERS

IITY, m/s

1—

? 6

LJU

-7

TURBir

—

// ^^v WATER

II *%

OIL

I 1 ! 1 1

RADIUS, mm

Figure 10.6. Turbine inlet velocity profiles for water and oil (Thompson and

Grey 1970; reproduced with permission from ASME).

They assumed that the retarding torque caused by bearing friction was negligible

compared with the aerodynamic forces, and they justified this on the grounds

that it is constant. They pointed out that the assumption was only valid for

commercial meters with low resisting torques.

c. They did not consider retarding torques apart from bearing friction and blade

aerodynamic drag.

They used this simple approach to examine the effect of flow profile and, know-

ing the profile downstream of a cone exit, to calculate meter error with distance

from the cone exit.

Hutton has made the point that a basic difficulty in applying blade theory to tur-

bine meters is that their blades are not very like flat plates because the parallelogram

-22 —

=> -44 —

S -66 -

-88

Figure 10.7. Driving torque per unit blade length for water and oil (Thompson

and Grey 1970; reproduced with permission from ASME).

10.2 PRECISION LIQUID METERS

221

Calibration constant shift

Turbine blade profile

Degree of

separation

Linearization by controlled flow separation

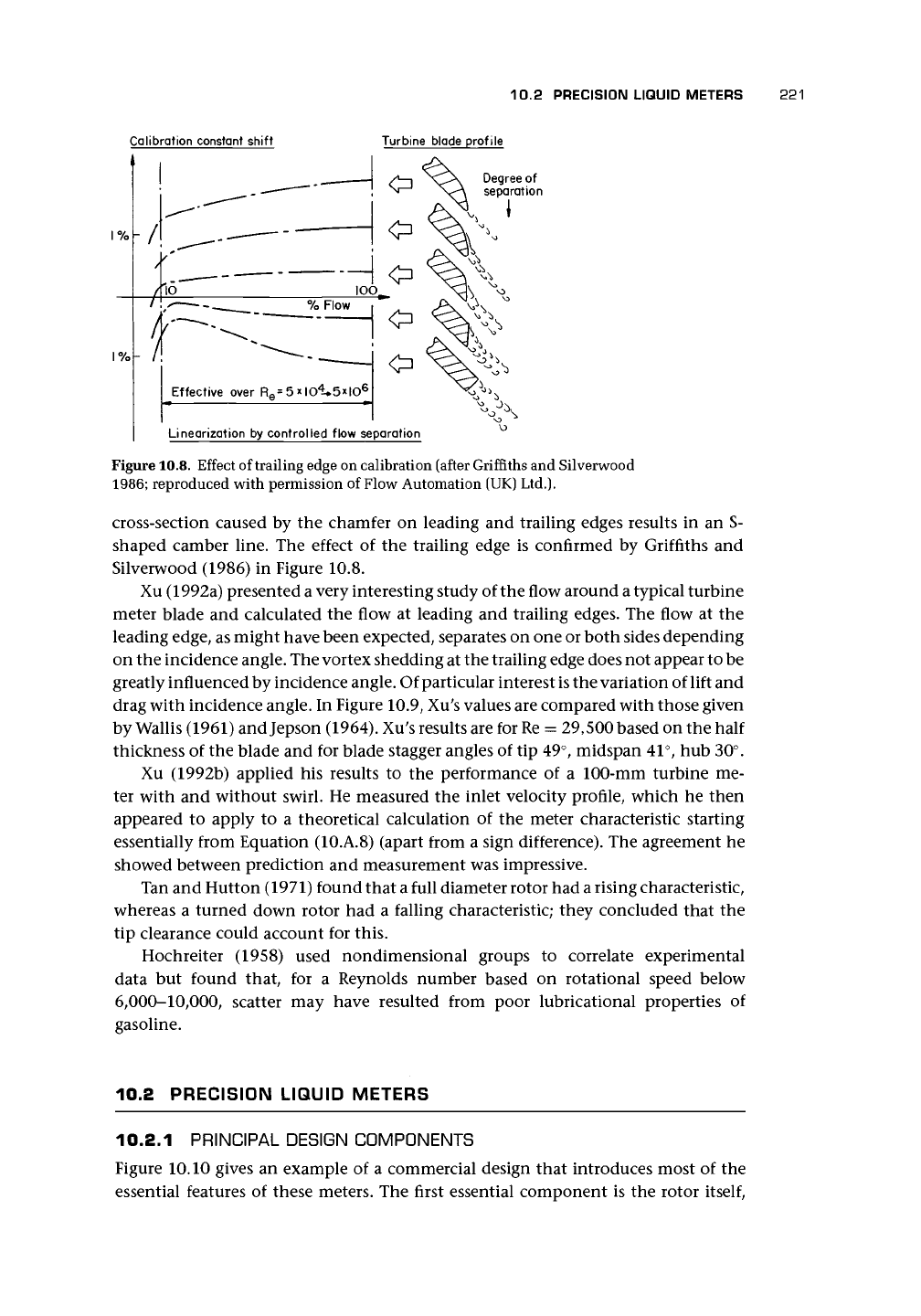
Figure 10.8. Effect of trailing edge on calibration (after Griffiths and Silverwood

1986;

reproduced with permission of Flow Automation (UK) Ltd.).

cross-section caused by the chamfer on leading and trailing edges results in an S-

shaped camber line. The effect of the trailing edge is confirmed by Griffiths and

Silverwood (1986) in Figure 10.8.

Xu (1992a) presented

very interesting study of the flow around a typical turbine

meter blade and calculated the flow at leading and trailing edges. The flow at the

leading edge, as might have been expected, separates on one or both sides depending

on the incidence angle. The vortex shedding at the trailing edge does not appear to be

greatly influenced by incidence angle. Of particular interest

the variation of lift and

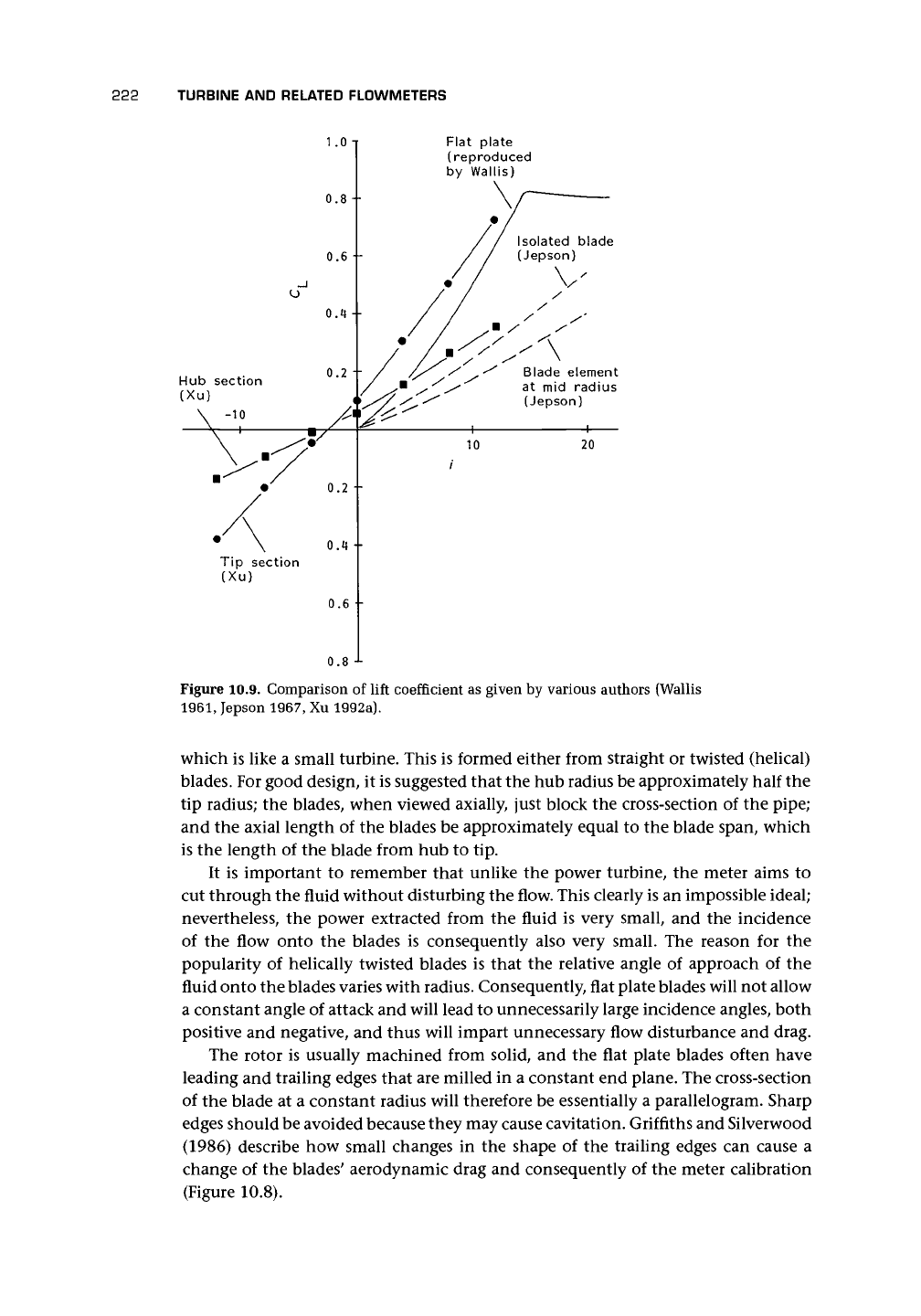
drag with incidence angle. In Figure 10.9, Xu

;

s values are compared with those given

by Wallis (1961) andjepson (1964). Xu's results are for

= 29,500 based on the half

thickness of the blade and for blade stagger angles of tip 49°, midspan 41°, hub 30°.

Xu (1992b) applied his results to the performance of a 100-mm turbine me-

ter with and without swirl. He measured the inlet velocity profile, which he then

appeared to apply to a theoretical calculation of the meter characteristic starting

essentially from Equation (10.A.8) (apart from a sign difference). The agreement he

showed between prediction and measurement was impressive.

Tan and Hutton (1971) found that a full diameter rotor had a rising characteristic,

whereas a turned down rotor had a falling characteristic; they concluded that the

tip clearance could account for this.

Hochreiter (1958) used nondimensional groups to correlate experimental

data but found that, for a Reynolds number based on rotational speed below

6,000-10,000, scatter may have resulted from poor lubricational properties of

gasoline.

10.2 PRECISION LIQUID METERS

10.2.1 PRINCIPAL DESIGN COMPONENTS

Figure 10.10 gives an example of a commercial design that introduces most of the

essential features of these meters. The first essential component is the rotor

itself,

222 TURBINE AND RELATED FLOWMETERS

-i

0.8 -

0.6 --

0.4 --

0.2 "-

Tip section

(Xu)

0.2 •

0.4

0.6

0.8

Flat plate

(reproduced

by Wallis)

Blade element

at mid radius

(Jepson)

Figure 10.9. Comparison of lift coefficient as given by various authors (Wallis

1961,

Jepson 1967, Xu 1992a).

which is like a small turbine. This is formed either from straight or twisted (helical)

blades. For good design, it is suggested that the hub radius be approximately half the

tip radius; the blades, when viewed axially, just block the cross-section of the pipe;

and the axial length of the blades be approximately equal to the blade span, which

is the length of the blade from hub to tip.

It is important to remember that unlike the power turbine, the meter aims to

cut through the fluid without disturbing the flow. This clearly is an impossible ideal;

nevertheless, the power extracted from the fluid is very small, and the incidence

of the flow onto the blades is consequently also very small. The reason for the

popularity of helically twisted blades is that the relative angle of approach of the

fluid onto the blades varies with radius. Consequently, flat plate blades will not allow

a constant angle of attack and will lead to unnecessarily large incidence angles, both

positive and negative, and thus will impart unnecessary flow disturbance and drag.

The rotor is usually machined from solid, and the flat plate blades often have

leading and trailing edges that are milled in a constant end plane. The cross-section

of the blade at a constant radius will therefore be essentially a parallelogram. Sharp

edges should be avoided because they may cause cavitation. Griffiths and Silverwood

(1986) describe how small changes in the shape of the trailing edges can cause a

change of the blades' aerodynamic drag and consequently of the meter calibration

(Figure 10.8).

10.2 PRECISION LIQUID METERS 223

Figure 10.10. Precision commercial turbine flowmeter design for liquids for

100—500 mm diameter (1, body; 2, rotor; 3, support nut; 4, support plate; 5,

support tube; 6, support vane; 7, lock tab; 8, end support assembly; 9, flange;

10,

pickup assembly; 11, pickup stub) [reproduced with permission of Flow

Automation (UK)

Ltd.].

The hangers or support vanes that position the bearings centrally in the pipe are

commonly used as flow straighteners to reduce swirl. Their shape varies considerably.

In Figure 10.10, they are flat plates, and in another design, they are parallel

tubes.

The

rotation of the rotor is sensed by a pickup, which most commonly senses a change

in the magnetic material permeability in its vicinity as a blade passes (magnetic

reluctance change). Alternatives to this are to use the eddy current effect or dynamo

effect as a blade passes through the magnetic field of the sensor (magnetic inductive)

or to use a modulated high frequency signal (modulated carrier or radiofrequency).

The capacitance effect can also be used to sense the proximity of a passing blade to

the sensor head. Optical fibers have been tried, but if the optical path passes through

the fluid, there is a danger of the windows becoming fouled. For increased integrity,

some meters have two sensors spaced at about 120°, the pulse trains from both are

sensed, and the phase angle is constantly checked.

In small meters, the internals are held in position by circlips, the removal of

which allows the internals to be withdrawn. In other designs and larger sizes, the

bearing assemblies may be removed from the body by releasing a taper locking nut.

10.2.2 BEARING DESIGN MATERIALS

Minkin et al. (1966) attributed calibration unpredictability to bearing variation as a

major factor.

Clean Liquids

Open ball bearings of stainless steel or other compatible material are suitable for

liquids with lubricating properties in the temperature range -50 to 250°C, but a

224 TURBINE AND RELATED FLOWMETERS

filter with a mesh size small enough to prevent solid particle ingress into the bearings

should be used.

Liquids in General

Tungsten carbide or high chrome/high cobalt journal bearings possibly with carbide

pinions and a stellite sleeve are suitable in the range —50 to 400°C unlubricated.

The bearings are lubricated by the metered fluid and made up of tungsten carbide

with a hardness of Rockwell C-94 and a surface smoothness of 0.05 /xm. Tungsten

carbide with cobalt bonding is most common, but the cobalt is leached out by acidic

solutions used for cleaning. Stellite may then be used as a less durable alternative

for more corrosive fluids.

more recent alternative is nickel-bonded carbide bushes

with titanium carbide shafts. An alternative design uses rotor pins of hard metal in

sapphire bearings with thrust plate and rings made with curved contact surfaces for

line contact. Polytetrafluoroethylene (PTFE) is used in some applications. Ceramic

bearings (e.g., A1

), may also be an option.

One manufacturer has used a ball-and-sleeve design. The shaft was tipped with

an ellipsoid and ran in a ceramic sleeve so that line contact was achieved. Typi-

cal bearing life was claimed as 12-24 months when used with 50-75% duty cy-

cle in clean particulate-free gasoline. For ball race bearings correctly lubricated, a

life of 4,000-6,000 hours was claimed, and for journal bearings 20,000 hours or

more was claimed, depending upon the properties of the measured fluid and rate of

flow.

For some larger sizes (above about 80 mm) only an upstream bearing is used; it

consists of a tungsten carbide (or other suitable materials) bush and shaft. Special

bearings are available for cryogenic applications (cf. Rivetti et al. 1987). Hydrostatic

bearings may be suitable for dirty fluids. House and Johnson (1986) applied hydro-

static bearings and obtained a remarkable performance (turndown ratio for water

1,000:1)

and suitability for dirty fluids. Wemyss and Wemyss (1975) described

the development of the Hoverflo bearingless meter. Some manufacturers provide

application charts.

Ball bearings have been found satisfactory for cryogenic applications in rocket

testing because of their ability to tolerate overspeed and operation with

gas.

However,

journal bearings, although less linear, may be more repeatable.

10.2.3 STRAINERS

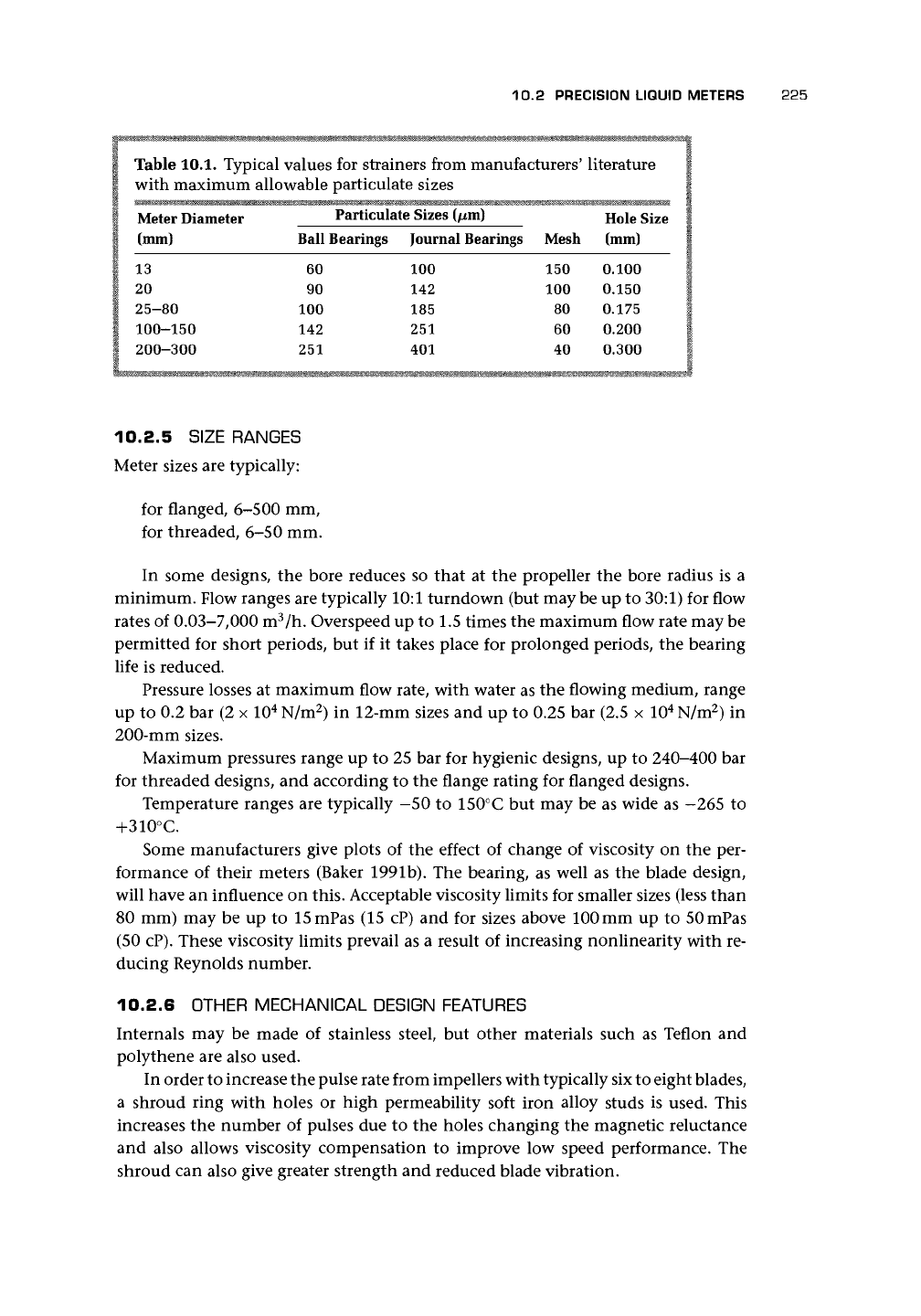
Typical values for strainers are given by manufacturers with maximum allowable

particulate sizes (Table 10.1).

10.2.4 MATERIALS

Because the signal is usually obtained from magnetic sensing, it is common to make

the tube of austenitic stainless steel to allow the magnetic field to penetrate. How-

ever, carbon steel is used for flanges and sometimes also for the bodies; in this in-

stance, provision is made for the pickup assembly to function despite the magnetic

body.

10.2 PRECISION LIQUID METERS 225

Table 10.1. Typical values for strainers from manufacturers' literature

with maximum allowable particulate sizes

Meter Diameter

(mm)

25-80

100-150

200-300

rariicuia

Ball Bearings

100

142

251

ie sizes t/xmj

Journal Bearings

100

142

185

251

401

Mesh

150

100

Hole Size

(mm)

0.100

0.150

0.175

0.200

0.300

10.2.5

SIZE RANGES

Meter sizes are typically:

for flanged, 6-500 mm,

for threaded, 6-50 mm.

In some designs, the bore reduces so that at the propeller the bore radius is a

minimum. Flow ranges are typically 10:1 turndown (but may be up to 30:1) for flow

rates of 0.03-7,000 m

/h. Overspeed up to 1.5 times the maximum flow rate may be

permitted for short periods, but if it takes place for prolonged periods, the bearing

life is reduced.

Pressure losses at maximum flow rate, with water as the flowing medium, range

up to 0.2 bar (2 x 10

N/m

) in 12-mm sizes and up to 0.25 bar (2.5 x 10

N/m

) in

200-mm sizes.

Maximum pressures range up to 25 bar for hygienic designs, up to 240-400 bar

for threaded designs, and according to the flange rating for flanged designs.

Temperature ranges are typically -50 to 150°C but may be as wide as -265 to

+310°C.

Some manufacturers give plots of the effect of change of viscosity on the per-

formance of their meters (Baker 1991b). The bearing, as well as the blade design,

will have an influence on this. Acceptable viscosity limits for smaller sizes (less than

80 mm) may be up to 15mPas (15 cP) and for sizes above 100 mm up to 50mPas

(50 cP). These viscosity limits prevail as a result of increasing nonlinearity with re-

ducing Reynolds number.

10.2.6 OTHER MECHANICAL DESIGN FEATURES

Internals may be made of stainless steel, but other materials such as Teflon and

polythene are also used.

In order to increase the pulse rate from impellers with typically six to eight blades,

a shroud ring with holes or high permeability soft iron alloy studs is used. This

increases the number of pulses due to the holes changing the magnetic reluctance

and also allows viscosity compensation to improve low speed performance. The

shroud can also give greater strength and reduced blade vibration.

226 TURBINE AND RELATED FLOWMETERS

In some small designs of turbine meter, the blades have a T shape so that at the

tip they are longer (longer chord) than at the hub. One reason given for this is to

improve insensitivity to viscosity change, which may result from a greater driving

torque achieved by increasing the blade lift at the maximum radius. It may also

flatten the characteristic hump at low speed. I am not aware of published data to

confirm these tendencies.

Some designs can be used bidirectionally, but, of course, they require calibration

in each direction.

Response time constants measured with water or with a liquid of similar density

range from 0.005 to 0.05 s for a 50% flow rate change or up to 0.17 s to reach 63%

of a step change final value.

After use with corrosive fluids, the meter should be cleaned with solvents. How-

ever, maximum rotational speeds should be carefully observed.

10.2.7 CAVITATI0N

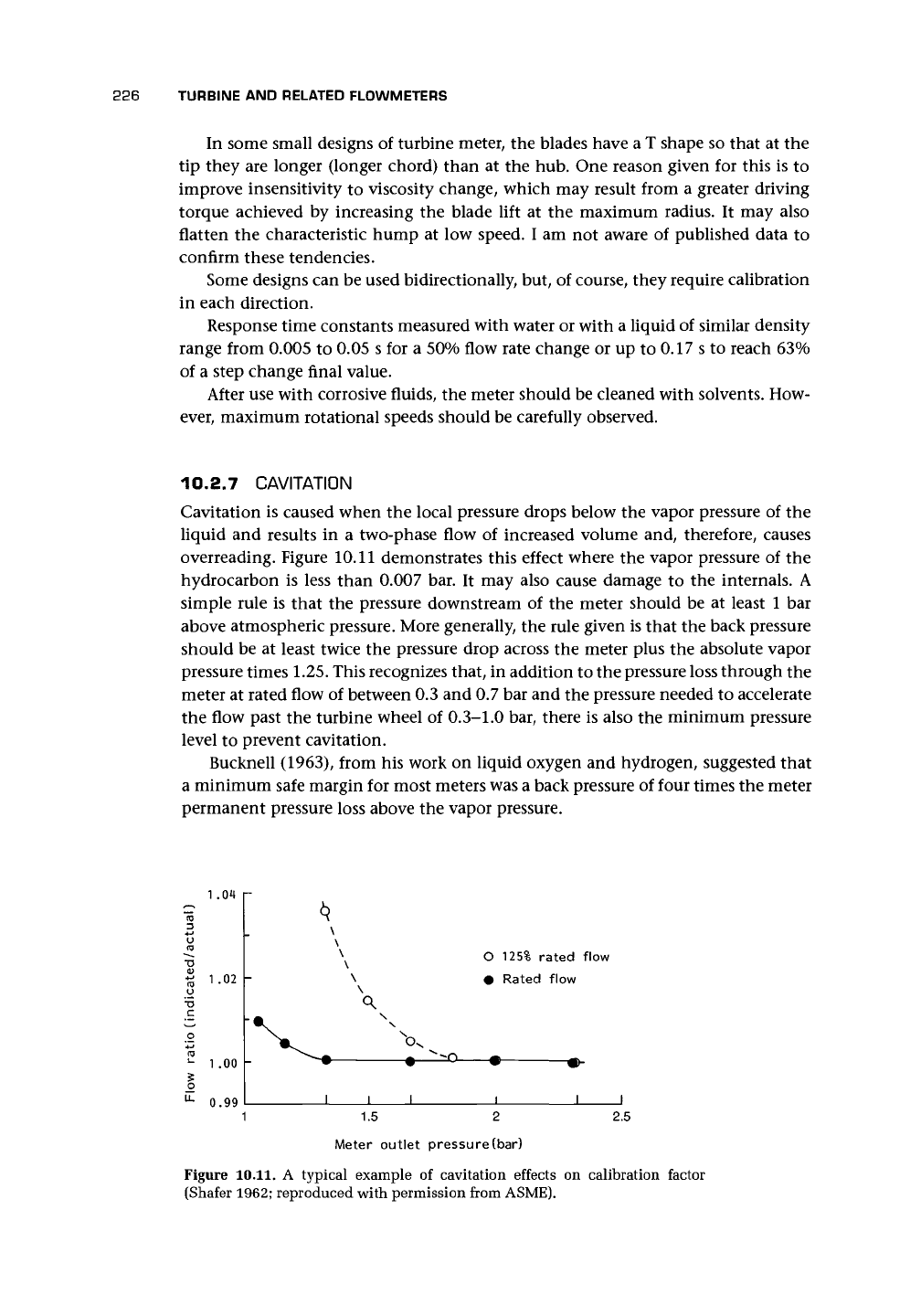
Cavitation is caused when the local pressure drops below the vapor pressure of the

liquid and results in a two-phase flow of increased volume and, therefore, causes

overreading. Figure 10.11 demonstrates this effect where the vapor pressure of the

hydrocarbon is less than 0.007 bar. It may also cause damage to the internals. A

simple rule is that the pressure downstream of the meter should be at least 1 bar

above atmospheric pressure. More generally, the rule given is that the back pressure

should be at least twice the pressure drop across the meter plus the absolute vapor

pressure times 1.25. This recognizes that, in addition to the pressure loss through the

meter at rated flow of between 0.3 and 0.7 bar and the pressure needed to accelerate

the flow past the turbine wheel of 0.3-1.0 bar, there is also the minimum pressure

level to prevent cavitation.

Bucknell (1963), from his work on liquid oxygen and hydrogen, suggested that

a minimum safe margin for most meters was a back pressure of four times the meter

permanent pressure loss above the vapor pressure.

1.04

1-02

1.00

^ 0.99

O 125% rated flow

\ • Rated flow

J I I

1 1.5 2 2.5

Meter outlet pressure (bar)

Figure

10.11.

A typical example of cavitation effects on calibration factor

(Shafer 1962; reproduced with permission from ASME).