Baker R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications

Подождите немного. Документ загружается.

9.A.1 FLOWMETER EQUATION 207

The successful use of positive displacement meters in such a hostile environment

as oil-well flows suggests that other difficult applications may be within range.

Total blockage of the line in the event of failure is, perhaps, the greatest disad-

vantage, and ways of dealing with this through an automatically controlled bypass,

in the event of blockage, may overcome this problem.

APPENDIX

9.A

Theory for a Sliding Vane Meter

The theory of the meter was set out by Hahn (1968). In his paper he considered the

motion of the vanes and calculated the radial velocity and acceleration if the internal

controlling cam gave a sinusoidal motion. He noted that the resultant forces between

vane and wall contributed to the wear of the vanes. Avoidance of jerky motion and

shock stresses is clearly important.

He also calculated the volumetric flow rate (cf. Baker and Morris 1985 whose work

was in ignorance of that due to Hahn). Hahn pointed out that the radial motion of

the vanes results in a sinusoidal fluctuation superimposed on the volume versus

rotation characteristic and that the amplitude of this fluctuation can be of order

0.05-0.1%

for various designs. This, in turn, would be shown in an irregularity

of the rotation of the shaft of as much as

1.25%.

However, in practice there will

be a balance between varying flow, pressure variation, and rotor velocity variation.

Hahn also gave characteristics showing variation of within 0.2% over a range of 14:1

(slight drop of

1.5-2%

with increasing flow) and changes of +0.15% for a change in

viscosity from 0.75 to 4 cP.

9.A.1 FLOWMETER EQUATION

The ideal behavior of the meter is given by the product of transferred volume, the

number of volumes transferred per revolution, and the rotational speed. For the ac-

tual behavior allowance has to be made for the leakage that takes place past the mov-

ing rotors. The bulk volumetric flow for a meter of the sliding vane type is given by

= [n (r

- rf) -

- Leakage flow (9.A.I)

where £

is the axial length of the chamber. The flow in each gap (Figure 9.A.I) will

be governed by

(9.A.2)

where [i is the fluid velocity at y in the gap, t is the clearance, p

and pa are the

upstream and downstream pressures, L is the length of the clearance gap or, in the

case of the vanes, the thickness of the vanes, and

/JL

is the viscosity. This results in a

208 POSITIVE

DISPLACEMENT FLOWMETERS

Figure

9.A.I. Geometry of

leakage

path between fixed and moving parts of the

meter

(after Baker and Morris 1985).

velocity

distribution of

= ^-i (t-

and

volumetric

flow through the gap of

(Ai - Pd)., Ut

(9.A.3)

(9.A.4)

where

I is the axial length of the gap.

the rotor is stationary, this quantity

becomes

the slippage;

(9.A.5)

Ideally,

the liquid in the gap would be carried at the same speed as the rotor

blade:

(9.A.6)

(9.A.7)

(9.A.8)

From Equations (9.A.I) and (9.A.8) and assuming that the leakage can be taken as

the sum of leakage through clearances tj of length in the direction of leakage L

;

and in the direction perpendicular to the leakage lj and with velocity of moving

component [/,-,

<?ideal

= Uti

From

Equations (9.A.4) and (9.A.6)

^leakage

= ^ideal — <?v

\ut i (Pu-Pd)^

(9.A.9)

An expression for the pressure drop across the vanes is obtained from the torque

balance on the rotor. The turning force due to (p

- p

) will act on a vane and will

precisely balance the frictional torques caused by bearings, vane clearance spaces,

and readout mechanism:

(9.

10)

9.A.2 EXPANSION OF THE FLOWMETER DUE TO TEMPERATURE 209

where 7o is a constant torque and

T\N/N

max

is a speed-dependent torque. Part of the

torque

TiN/N

max

will be due to the clearance drag torque:

where r

;

is the radius from the rotational axis of the ;th clearance.

9.A.2 EXPANSION OF THE FLOWMETER DUE TO TEMPERATURE

If a

is the coefficient of linear expansion of the metal, then a change in temperature

of the metal of the flowmeter will cause a change in length

so that

^=3a

(9.A.12)

giving the fractional change in measured volume per revolution of the flowmeter

rotor.

Differential Expansion

If the expansion of the rotor differs from that of the casing due either to different

temperatures or to different materials, then the clearances will be designed for the

greatest relative movement between these members. The change in the value of the

clearance t will be

-=a

- (9.A.13)

between uniform temperature conditions and conditions when the temperature of

the internal rotor and the casing differ by A

7^.

For the case where the temperatures

are the same but the coefficients of expansion differ, this becomes

At r~

(9.A.14)

Liquid Density Change

The change in the bulk flow due to expansion of the liquid will be

(9.A.15)

where a

is the coefficient of volume expansion of the liquid.

Because many liquids are bought and sold by volume, this change is of

different

significance from those given before. The volume passed by the meter

may,

therefore,

be important. In some cases, the change in liquid density may be ignored.

210 POSITIVE DISPLACEMENT FLOW METERS

9.A.3 PRESSURE EFFECTS

Provided that the meter is supplied with an outer pressure vessel, there should be no

net pressure causing distortion of the inner meter. However, this is not invariably

so.

The meter will then suffer from two distortions, hoop stress and axial stress. For

convenience, we will consider these effects separately and ignore the effects of one

on the other.

Bulk Flow Error

If Ap is the difference between internal and external pressure and E is Young's mo-

dulus of elasticity, then the change in the outer radius will be

IT-IT

(9A16)

where £, is the thickness of the outer casing. The axial stress will cause an elongation

where £

is the axial length of the meter's measuring chamber. Together these lead

(neglecting Poisson

;

s ratio effects) to an increase in measuring volume, which causes

an error in the volumetric flow rate of

Leakage Gap

In certain designs, the hoop stress will cause an increase in the clearance of

Arc

rjAp

t t ttoE

v ;

whereas the axial stress will cause an increase in end clearance at each end of

At A£

4x Ap

t t

(9.A.20)

Clearly these calculations are simplifications of the actual expansion that will occur,

but they allow some estimate of likely errors to be made.

9.A.4 METER ORIENTATION

Bearings at Each End of Shaft

Assuming that the shaft behaves like a beam simply supported at each end and that

the rotor weight is evenly distributed along the shaft, then the maximum deflection

at the point midway between the bearings will be given by

Deflection =

SMgi

\ (9.A.21)

9.A.5 ANALYSIS OF CALIBRATORS

211

where

M is the

mass

of the

rotor,

g is

acceleration

due to

gravity,

and r

shaft

radius.

Bearing(s)

One End

Shaft Only

Assuming that,

this case, the bearing(s) hold the shaft without deflecting, the shaft

bending will be equivalent

to a

uniformly loaded encastre beam. The end deflection

of this, which will

be the

maximum value,

given

Mai

Deflection

y a

(9.A.22)

apparent that, other things being equal,

the

deflection

the end bearing shaft

will

nearly

times greater than

the

shaft with bearings

each end. This will

require greater clearances

and,

consequently, allow greater leakages.

avoid this

problem,

may be recommended that meters

mounted with shafts vertical.

9.A.5 ANALYSIS

CALIBRATORS

The rotation

these meters gives

the

volumetric flow.

every rotation causes

pulse,

it is a

simple matter with modern electronics

scale

the

pulse rate

give

any required calibration factor

combine

the

electrical output from

temperature

sensor

give

temperature compensation. However,

many applications,

me-

chanical calibration

and

temperature adjustment

required

as a

result

existing

installation constraints,

and

three main methods have been used

are possible.

Gearbox

The gearbox with interchangeable gears will

not be

discussed

this section.

The

drawback of the gearbox is clearly the limited adjustment possible. We are concerned

with

two

calibrators, which

may

introduce special features into

the

meter perfor-

mance.

Epicyclic System

A schematic diagram

this system

given

Figure

9.10. The

drive from

the

flowmeter shaft enters with rotation 2V

The

drive then divides.

The

main drive

via

gears tt\, n

, n

and so to the

epicyclic unit.

The

other

is via the

disk

and

adjustable friction wheel

The

recombined drives leave

the

epicyclic unit

via n

with rotation

A/OUT-

The integrity of the unit depends heavily on the wheel and

disk contact. There must

be no

slip between these components,

but

they must also

not wear and must be adjustable

the radius

frictional contact being changed by

the adjustment).

The ratio

UT/MN is given by

NOUT

^L ffcWs

rnn

NIM

[

\ n

where

R is the

radius

the friction wheel.

212 POSITIVE DISPLACEMENT FLOWMETERS

Putting typical values of the numbers of teeth

(ri)

into Equation (9.A.23)

= rii

20n

~15~

= Sn

then

NQUT

= 10 mm and we let r = 10 mm,

^^ = -0.508

Ifr = 11 mm,

1ST

-°-

503

or a change in calibration of 1%.

We may also write down the modified version of Equation (9.A.23), assuming

that a small amount of slip occurs between disk and wheel equivalent to a rotation

NIN.

Then

K™ = L

A d _

Hi!!*]

(i-**L\- ^^

(9.A.24)

R n

\ n

j \ N

) n

In this case, a relation between the torque in Ti

and the torque out T

m, the friction

force between wheel and disk F, is given by

(9.A.25)

At the start of rotation if N

UT were zero and Ni

were nonzero, then

NIN

and

= 1-

R n

V n

Using the values given earlier,

—5-

= -9.2

= -9.2 rF

9.A.6 APPLICATION OF EQUATIONS TO A TYPICAL METER 213

If slip does not occur, then

NOUT rj,

iiN = —j^— -four

NIN

-0.508

TOUT

With these relationships and the coefficient of friction, the required contact force

between wheel and disk can be estimated from a knowledge of the torque required

to operate the counter unit.

Clutch System

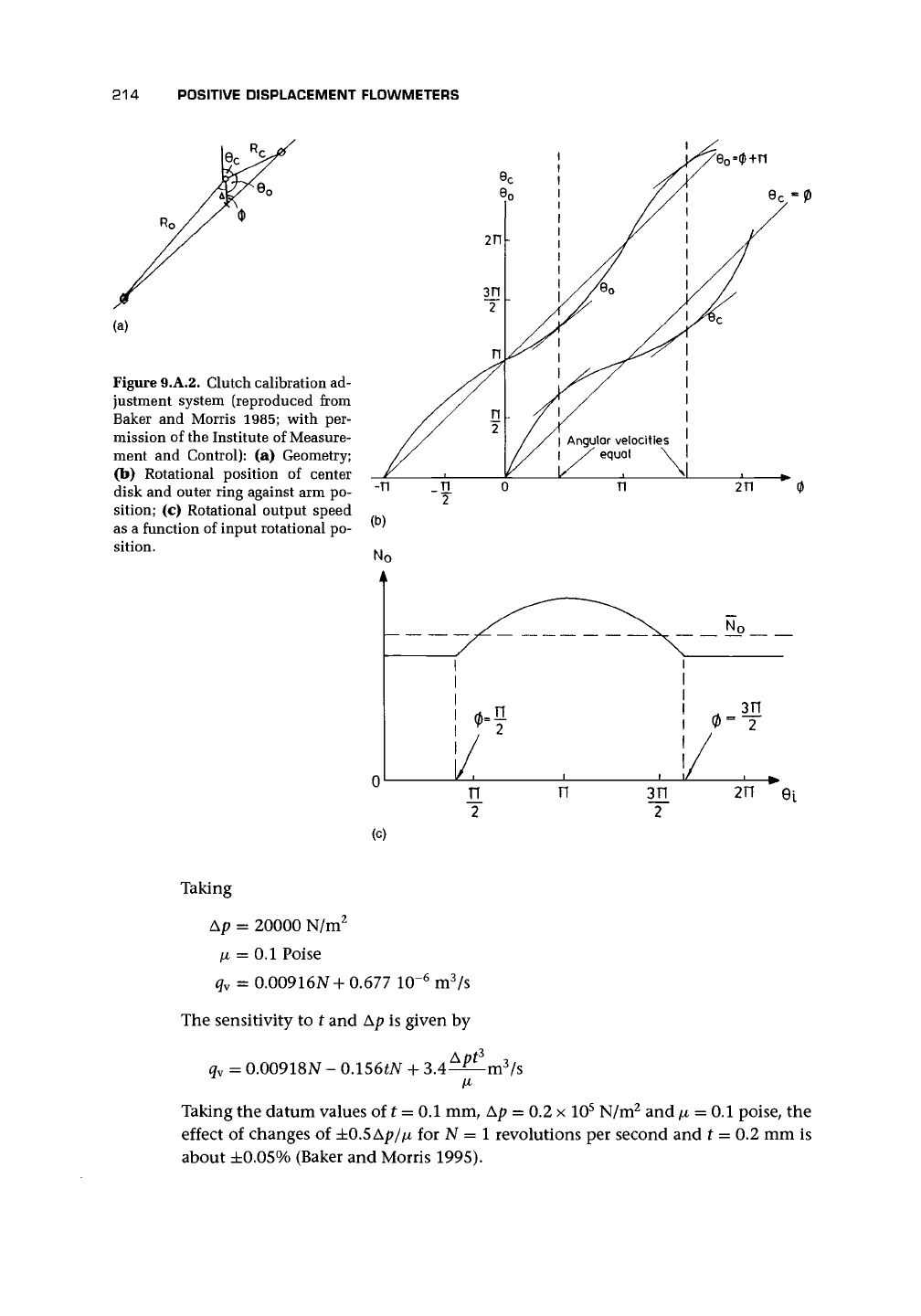
The clutch (or cam) system consists of three concentric disks and rings (Figure 9.11).

The central ring is driven by the input shaft and carries a series of clutches that lock

on the center disk and the outer ring, causing them to rotate at least as fast as the

central ring. An arm rotates on a separate shaft, which is not concentric with that

of the disk and rings. In this arm are two sliders, one fixed to, and rotating with, the

center disk and the other fixed to, and rotating with, the outer ring. Because of the

eccentricity of the arm shaft, the center disk and the outer ring are forced to rotate at

different speeds. The difference in speeds can be adjusted by manually altering the

amount of eccentricity. Thus, the speed at which the output shaft revolves relative

to the input shaft is adjusted to achieve compensation for use of the measuring

element under a particular set of operating conditions. It can be shown that if O is

the angular position of the arm and

and

are, respectively, the angular positions

of the center disk and outer ring [Figure 9.A.2(a)]

)

(9.A.26)

and

* =

+ tan"

(

\) -

* (9.A.27)

Acos^/

where A is the distance between the centers of rotation of the arm and the disks.

These are plotted in Figure 9.A.2(b), and it can be seen that at

<J>

= 0, n, and 2n

the angular positions differ by n. The angular velocities will be equal when, for a

given value of $, the slopes of

and 0

are equal.

In Figure 9.A.2(c), the relationship between output rotational speed N

and input

rotational position

(which for constant flow rate is proportional to time) is plotted.

It is important to note the nonuniform rotation of the output and the mean value

in relation to actual rotational speed at various points in the cycle.

9.A.6 APPLICATION OF EQUATIONS TO A TYPICAL METER

Using the meter with dimensions shown in Figure 9.13 and Equation (9.A.9), we

obtain for the main coefficients, assuming a total leakage length of 325 mm,

= 0.00918N

-0.0000156N (leakage)

+0.034 x

10~

—

(leakage due to pressure change)

214

POSITIVE DISPLACEMENT FLOWMETERS

Figure 9.A.2. Clutch calibration ad-

justment system (reproduced from

Baker

and

Morris 1985; with

per-

mission

the Institute

Measure-

ment

and

Control):

(a)

Geometry;

(b) Rotational position

center

disk

and

outer ring against arm po-

sition;

(c)

Rotational output speed

function

input rotational po-

sition.

1/.

!/ , .

3Tt

2T1

(c)

Taking

Ap = 20000 N/m

[i = 0.1 Poise

= 0.00916N + 0.677 10~

The sensitivity to t and Ap is given by

= 0.00918N - 0.156tN + 3

Taking the datum values of t = 0.1 mm, Ap = 0.2 x 10

N/m

and /x = 0.1 poise, the

effect of changes of ±0.5Ap//x for N = 1 revolutions per second and t = 0.2 mm is

about ±0.05% (Baker and Morris 1995).

CHAPTER

Turbine

and

Related Flowmeters

10.1 INTRODUCTION

10.1.1

BACKGROUND

Spirals, screws,

and

windmills have

long history

of use for

speed measurement.

Robert Hook proposed

small windmill

1681

for

measuring air velocity

and

later

one

for use as a

ship's

log

(distance meter).

Captain Phipps,

1773, created

ship's

log,

using

the

principle that

spiral,

turning, moves through

the

length

one

turn

of the

spiral. Many centuries earlier,

appears that

Roman architect,

Vitruvius, suggested

more basic form

this device.

In 1870 Reinhard Woltmann developed

multibladed

fan to

measure river flows

(Medlock 1986).

The

device

was a

forerunner

of the

long helical screw-type meter

still called after

him and

used widely

for

pipe flows

in the

water industry.

The

first

modern meters,

the type with which we are mainly concerned, were developed

the United States

in 1938

(Watson

and

Furness 1977;

cf.

Furness 1982). These were

attractive

for

fuel flow measurement

airborne applications. They consisted

of a

helically bladed rotor

and

simple bearings. Improved sleeve bearings were developed

for longer life with hardened thrust balls

endstones

withstand

the

axial load.

An alternative, developed over several years

and

patented

Potter (1961),

was to

profile

the hub of

the rotor

that

the

pressure balance across

the

rotor, rather than

the thrust

on the

bearings, held

against

the

axial drag forces. This allowed

the

rotor

to run on a

single journal bearing.

10.1.2

QUALITATIVE DESCRIPTION

OPERATION

The turbine consists

of a

bladed rotor that turns

due to the

flow

in the

pipe.

most

of the

designs

to be

discussed,

the

rotor

designed

create

the

minimum

disturbance

as the

oncoming flow passes around it. Ideally,

cuts perfectly through

the fluid

in a

helix

that every revolution

of the

helix represents

one

complete

axial length

of the

screw,

and

hence

calculable volume

of the

fluid.

practice,

there

are

drag forces, which slightly retard

the

rotation. These result from frictional

drag

on the

blades,

the

hub,

the

faces

the rotor,

and the tip of

the blades; bearing

drag, also

frictional effect;

and

drag

due to the

means

which

the

rotation

measured, which

usually

magnetic drag. These drag forces affect

the

otherwise

ideal relationship

constant fluid volume

for

each rotor revolution

and

lead

nonlinearity.

215

216

TURBINE AND RELATED FLOWMETERS

The rotor has to be held in the stream, and so supports are invariably necessary

to position the bearings centrally in the pipe. Virtue is made of necessity, and these

supports are used to provide some flow straightening, since the turbine meter is of a

type particularly susceptible to swirl. The oncoming fluid will therefore need to flow

over the upstream support, and the naturally occurring profile, where the velocity of

the fluid is lower at the pipe wall than at the center of the pipe, will be redistributed

into the annular passage past the

blades,

and, perhaps most importantly, there will be

a reduction in any swirl component due both to conservation of angular momentum

during the redistribution and to the straightening effect of the supports. The velocity

in this passage will vary a small amount with radial position, and a well-designed

turbine rotor will generally have helical blades to match the axial and tangential

velocity of the rotor at each radial position.

The main variants from this description are the Pelton and vane or paddle wheel

designs. In the former, a tangential jet of fluid hits the buckets or blades of the wheel

and causes them to rotate. This design has two alternative virtues: it can be made

as a simple insertion probe to obtain an estimate of the flow rate, or it can be used

in very small flows to register where other designs fail. Other designs using larger

paddle wheels and angled propellers are also available (cf. Baker 1991b, 1993).

10.1.3 BASIC THEORY

Many turbine meters use flat section blades. Ideally these will cut smoothly through

the flow in a perfect helix. Using this basic concept, the value of

can be obtained

from the frequency of blade passing f (Figure 10.1). Thus,

W/t<m/3

and

f=N tan

(10.1)

(10.2)

where V

is the axial velocity of the flow approaching the blades, W is the blade

velocity,

is the blade angle, N is the number of blades, and r is the radius of the

blades at the measurement point.

Equation (10.2) can be used to obtain

f=Kq

(10.3)

Figure 10.1. Relationship between velocities and angles for ideal flow over

blades.