Baker R.C. Flow Measurement Handbook: Industrial Designs, Operating Principles, Performance, and Applications

Подождите немного. Документ загружается.

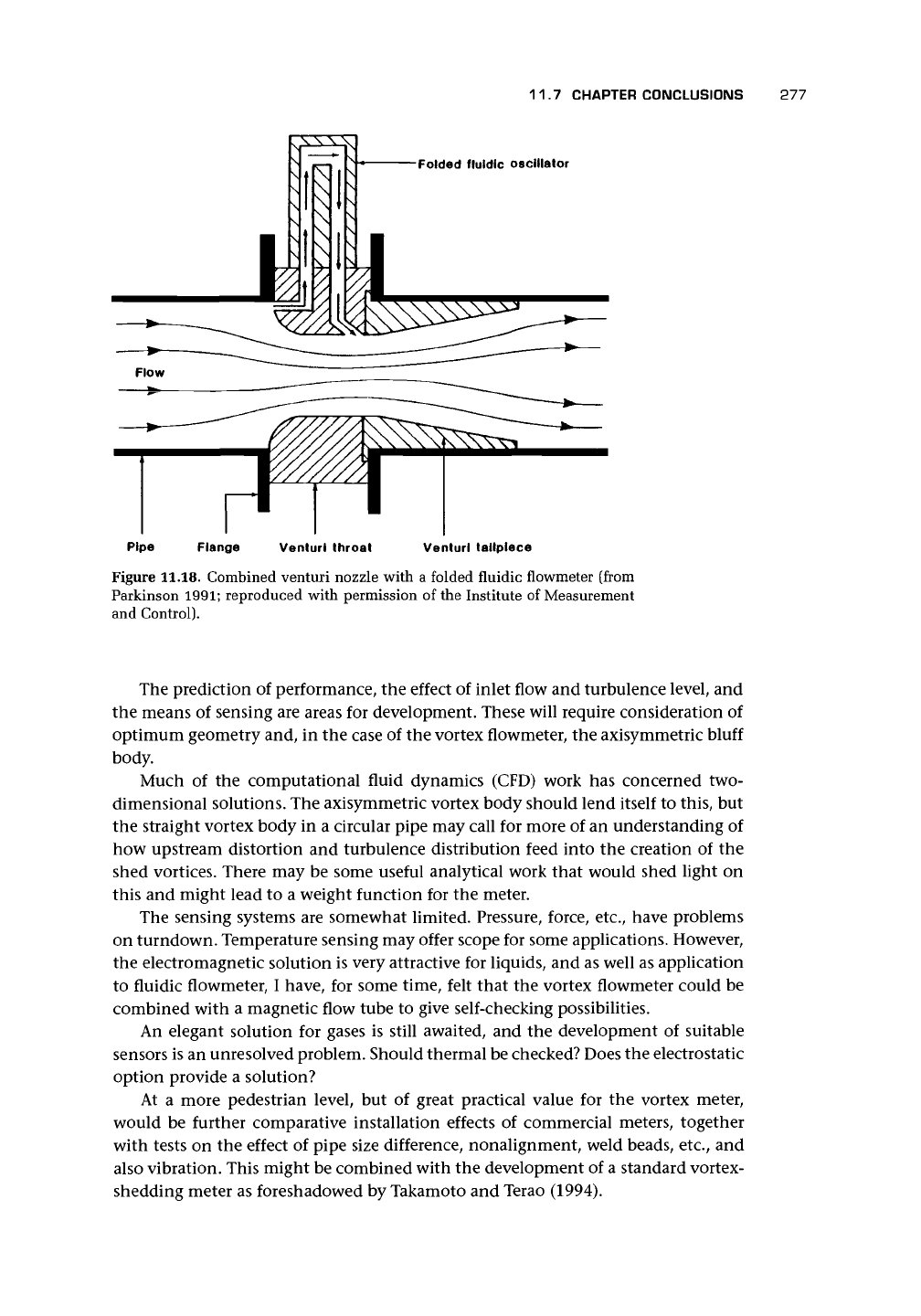
11.7 CHAPTER CONCLUSIONS

277

Folded fluidic oscillator

Pipe

Flange

Venturi throat

Venturi tailpiece

Figure 11.18. Combined venturi nozzle with a folded fluidic flowmeter (from

Parkinson 1991; reproduced with permission of the Institute of Measurement

and Control).

The prediction of performance, the effect of inlet flow and turbulence level, and

the means of sensing are areas for development. These will require consideration of

optimum geometry and, in the case of the vortex flowmeter, the axisymmetric bluff

body.

Much of the computational fluid dynamics (CFD) work has concerned two-

dimensional solutions. The axisymmetric vortex body should lend itself to this, but

the straight vortex body in a circular pipe may call for more of an understanding of

how upstream distortion and turbulence distribution feed into the creation of the

shed vortices. There may be some useful analytical work that would shed light on

this and might lead to a weight function for the meter.

The sensing systems are somewhat limited. Pressure, force, etc., have problems

on turndown. Temperature sensing may offer scope for some applications. However,

the electromagnetic solution is very attractive for liquids, and as well as application

to fluidic flowmeter, I have, for some time, felt that the vortex flowmeter could be

combined with a magnetic flow tube to give self-checking possibilities.

An elegant solution for gases is still awaited, and the development of suitable

sensors is an unresolved problem. Should thermal be checked? Does the electrostatic

option provide a solution?

At a more pedestrian level, but of great practical value for the vortex meter,

would be further comparative installation effects of commercial meters, together

with tests on the effect of pipe size difference, nonalignment, weld beads, etc., and

also vibration. This might be combined with the development of a standard vortex-

shedding meter as foreshadowed by Takamoto and Terao (1994).

278 VORTEX-SHEDDING, SWIRL, AND FLUIDIC FLOW METERS

The fluidic meter appears to have found a particular niche in the utilities, and

several are being, or have been, developed. They appear to offer a large turndown,

provided a suitable sensing system is available. One such system is the magnetic

system developed (Sanderson 1994) for water flows.

The CFD analysis of the fluidic flowmeter is also, mainly, two-dimensional, but

the effect of end walls and the turbulence level of the inlet flow may need fur-

ther assessment, and it seems unlikely that the internal geometry has been finally

optimized.

At the opposite extreme would be the investigation of intrinsic flow noise due

to vortex shedding in existing pipework, which could be sensed and calibrated as a

flowmeter system. If such noise exists, an intelligent sensor could learn its calibration

and then provide for a utility measurement.

The continuing development of these meters in terms of range, reliability, low

maintenance, accuracy, and price should ensure that they establish a respected place

in the options for flow measurement.

APPENDIX

1 1.A

Vortex-Shedding Frequency

11.A.1 VORTEX SHEDDING FROM CYLINDERS

Flow around a cylindrical body develops as in Figure

11.1.

At a low Reynolds number

[Figure 11.1

(a)],

the flow pattern on each side of the cylinder is almost symmetrical

(for Re < 1 there is symmetry cf. Tritton 1988). The symmetry between the flow

approaching the cylinder from upstream and that leaving it downstream is removed

with increasing

Re.

When Re exceeds about 4 (Tritton 1988), eddies, which are more

or less symmetrical [Figure ll.l(b)], are formed behind the cylinder and, as shown

in Figure ll.l(c), start to become unsymmetrical before a Reynolds number of about

40 is reached. It is from this point that we obtain the remarkable phenomenon of

vortex shedding.

The lack of symmetry in Figure ll.l(c) breaks down into a periodic flow as

illustrated in Figure ll.l(d). At this stage, the flow is stable and viscous (Roshko

1954).

The boundary layer on the cylinder and the shear layer in the wake are pre-

sumably laminar. The shedding is very regular in this region. In the range omitted

from Figure 11.1, namely 150 < Re < 300 (or 200 < Re < 400 according to Tritton),

transition from laminar to turbulent takes place in the shear layer, and the transi-

tion is accompanied by less regular shedding. Once the regime in Figure ll.l(e) is

reached, the shedding becomes regular once more.

further transition in the region

3 x 10

< Re < 3 x 10

occurs as the boundary layer changes from laminar to turbu-

lent causing irregularity (Tritton 1988). In this case, Tritton illustrates the laminar

separation followed by turbulent reattachment and then, again, the occurrence of

separation. The regime in Figure ll.l(f) has regular shedding and a later separation

point. Tritton comments that markedly periodic shedding remains a characteristic

of the flow up to the highest values of Reynolds number at which observations have

been made, about 10

11.A.2

ORDER

MAGNITUDE CALCULATION

SHEDDING

FREQUENCY

279

11.A.2 ORDER OF MAGNITUDE CALCULATION

OF SHEDDING FREQUENCY

Using a numerical solution, Abernathy and Kronauer (1962) showed that two shear

layers result in the build-up of large vortex regions. Their diagrams also showed

that one shear layer gets caught in the other shear layer and eventually results

in a region where vortices of opposite sense cancel each other and break the

shear layer (cf. Robinson and Saffman 1982 on the stability of Karman vortex ar-

rays).

Figure 11.2 is a simple diagram of this mechanism (cf. Figure 11.14). In Figure

11.2(a),

one vortex has just separated and the next is beginning to roll up. The roll-

up is caused by the influence of each new vortex on those that have gone before.

In Figure 11.2(b), the large vortex roll has curled back on itself and has started to

entrain the vortex sheet of opposite sense on the other side of the body. In Figure

11.2(0),

this entrainment has advanced to the point where the upper vortex sheet is

nullified and the roll-up of the vortex is stopped as the whole vortex roll is set free

(cf. Gerrard 1966).

A simple model to obtain a value for the roll-up time of the large vortex is given

by Figure 11.A.I. The vorticity shed will be of order V/8, where 8 is the shear layer

thickness. The rate of shedding will be approximately the mean velocity in the shear

layer V/2 multiplied by the layer thickness

Thus vorticity shedding rate is

V 8V _ V

T~T

The vorticity has to fuel a vortex with a diameter approximately equal to the size

of the bluff body. The total vorticity within this roll will be

V x V

•

Vds

= TTWV

The time to fill a vortex of diameter w with nw V is approximately

TTWV

Thus an order of magnitude value for the frequency again is

f =

2TTW

(11.A.1)

Vorticity

Figure ll.A.l. Simple model of vortex shedding.

280 VORTEX-SHEDDING, SWIRL, AND FLUIDIC FLOWMETERS

useful parameter is the Strouhal number given by

5= fw/V (11.A.2)

and using the approximation of Equation (ll.A.l) we obtain a value of

= l/(27r) =

0.16. Goldstein (1965) gave 0.18 for a circular cylinder at a Reynolds number in the

range 300-100,000.

Because of the reduced cross-section of the flowmeter due to the presence of a

bluff body, the actual velocity past the body

max

will be greater than that in the

upstream pipe V. For an incompressible fluid, area x velocity is constant. The area

ratio will be given approximately by

Thus for an incompressible fluid

Vmax

V 1 -

4W/TTD

(11.A.4)

and so combining Equations (11.A.2) and (11.A.4) and assuming the appropriate

velocity for Equation (11.A.2) is

max

we obtain

45 1

(H.A.6)

VrP

(w/D)(l-4w/jrD)

and so the approximate Strouhal number of 0.16, which we obtained based on the

flow past the body will apparently be increased if based on the velocity in the main

pipe according to Table ll.A.l. For comparison, Takamoto and Terao (1994), for a

w/D of 0.28, give S in the range 0.245-0.265 for Re from 10

to 10

. The limitations

of this simple approximation are shown by the effect of change in length of the bluff

body from 0.4D to 0.2D found by Takamoto and Terao.

Zanker and Cousins (1975) assumed that the roll vortex was slightly larger than

the bluff body diameter by between about 10 and

50%.

This created a vena contracta

confining the flow downstream of a sharp-edged bluff body to a smaller area near

the wall in which the maximum velocity increases more. Adding their factor K to

Equation (11.A.6), we obtain the same equation as they did:

_ 45 1

Table ll.A.l. Approximate variation of

^ ~

^~Q3

(

/D)(l

- AKw/nD)

Strouhal number based on mean pipe

1 A

velocity for various body sizes

. , It is arguable that a further K should

linux/V 5 corrected appear as a multiplier in the denomina-

o.l 1.15 0.18 tor to allow for the larger vortex, which

0.3 1.62 0.26

has to be filled. However, this is proba-

05 2

°-

'. bly stretching a simple model too far, but

. . interestingly it appears that for a w/D of

11.A.2 ORDER OF MAGNITUDE CALCULATION OF SHEDDING FREQUENCY 281

about 0.3, this extended form of the denominator is less affected by the value of K

than for, say, 0.1 or 0.5.

One can see how the change in the upstream conditions could influence the

shedding frequency. Upstream disturbances will alter the vorticity in the flow and

so reduce or increase the frequency of shedding and possibly the regularity. These

changes are illustrated by Mottram (1991) for the effect of a more peaky profile due

to pipe roughness and an increased Strouhal number. In this case, both the increase

in local velocity at the body and the increase in vorticity will have effects. Other

results discussed in this chapter show, surprisingly, that this type of meter is quite

susceptible to the effect of a reducer upstream, presumably again because of the

effect on the turbulence spectrum.

Terao et al. (1993) made two interesting observations.

• Vortices moved faster downstream than the mean velocity.

• Areas of intense vorticity existed at the wall.

The first of these two must affect the use of vortex shedding with cross-correlation

techniques. The second suggests that three-dimensional computational solutions

must include this observation (cf. Majumdar and Gulek 1981 for an early paper on

shedding from various prisms).

CHAPTER

Electromagnetic Flowmeters

12.1 INTRODUCTION

The possibility of inducing voltages in liquids moving through magnetic fields was

known by Faraday in 1832, but the first flowmeter-like device was reported by

Williams in 1930. The first real advance in the subject came from the medical field

where Kolin (1936, 1941) introduced many ideas that are now standard practice.

The industrial interest in electromagnetic flowmeters (sometimes referred to as

EM or magnetic flowmeters) grew in the 1950s with

• the Tobiflux meter (Tobi 1953) in Holland for rayon viscose, sand and water, and

acid slurries;

• Foxboro, to whom the patent was assigned in 1952;

• the first commercial instruments in 1954 (Balls and Brown 1959).

• nuclear reactor applications;

• the work that resulted in an essential book by

A. Shercliff (1962).

In this chapter, we shall concentrate on the application of the flowmeter to fluids

that are of low conductivity, such as water-based liquids (Baker 1982). The flowmeter

has also been used with liquid metals (Baker 1969, 1970b, 1977), and a few designs

have been built for use with nonconducting dielectric liquids (Al-Rabeh et al. 1978).

The reader is referred to the original papers because space prevents their inclusion

here.

Three papers by Wyatt

(1961,

1977, 1982), a pioneer in blood flow measure-

ment research, are referenced for those interested.

12.2 OPERATING PRINCIPLE

We start with the simple induction, which occurs when a conductor moves through

a magnetic field. Figure 12.1 shows a copper wire cutting the flux of a permanent

magnet. The wire is moving in a direction perpendicular to its length and per-

pendicular to the magnetic field with velocity V, and the result is a voltage gen-

erated between its ends of value BIV where / is its length and B is the magnetic flux

density.

Figure 12.2 shows a diagram with the essential features of an electromagnetic

flowmeter. The liquid flows in a circular cross-sectional tube.

magnetic field is cre-

ated across the pipe, usually by coils excited by an alternating current. The tube itself

282

12.2 OPERATING PRINCIPLE 283

must be made from nonmagnetic material

so that the magnetic field can penetrate

the tube. In this diagram, we may imagine

filaments of liquid spanning the tube from

one electrode to the other and moving

through the magnetic field at different

speeds generating voltages between their

ends as was the case with the copper wire.

To avoid these being shorted out, the

tube is lined with an insulating material.

The voltages in the liquid are measured

between electrodes, which are set in the

wall of the tube.

Referring now to Figure 12.3, we have

depicted the case where more than one wire

is moving through the magnetic field. Wire

is in a region of strong magnetic

field

and has a velocity V. Wire Q

in a region where the field is about the same size, but

it only has a velocity V/2. Wire

although moving with velocity V, is in a region of

weak magnetic field, say, B/4. Thus the magnetic induction in each will be different:

Figure

12.1.

A wire moving through

magnetic field

generates

potential difference between

its

ends.

InP

InQ

InR

A£/

BIV

AL/Q

= BlV/2

Al/

= BlV/4

(12.1)

Now if the ends of the wires are connected, currents will flow because the po-

tentials differ, and the result will be that A£/

will be reduced by the ohmic loss.

Carrying this same argument back to Figure 12.2 results in a complicated picture

of voltages and circulating currents. Despite this apparent complexity, the actual

operating equation of the flowmeter is quite simple for a range of conditions. The

voltage between the electrodes is given by

AL/

= BDV

(12.2)

Tube

Flow

Electrodes

Magnet

Figure

12.2.

Simple

flowmeter.

284

ELECTROMAGNETIC FLOWMETERS

Figure 12.3. Three wires moving through a magnetic

field of varying spatial strength at different speeds.

where B is the magnetic flux density in

tesla, D is the diameter of the tube in me-

ters,

and V^ is the mean velocity in the tube

in meters per second.

This is the basic equation for the flow-

meter, and it can be shown to be valid only

when

• the magnetic field is uniform and

• the velocity profile is axisymmetric.

In modern designs, these requirements

are seldom satisfied, and so designs have been developed to give an output signal that

is as little affected by the flow profile as possible, in compact designs with magnetic

fields far from uniform.

12.3 LIMITATIONS OF THE THEORY

Uniform Field

- It can be shown that in theory the only field that is uniform is

one from a magnet of infinite extent.

Axisymmetric

Profile

- All fully developed pipe flow profiles are axisymmetric.

But it is not always convenient to allow the necessary upstream pipe length to

ensure a fully developed profile.

Shercliff (1962) suggested a means of predicting the effect of distorted profiles

using what he called a weight function (Appendix 12.A). He calculated the shape

of this function for a uniform magnetic field meter [Figure 12.4(a)]. In its simplest

form, this indicates how important the flow is in any part of the pipe cross-section

and how great its influence will be on the flow signal. The velocity at each point

in the cross-section of the flowmeter is multiplied by the weight function. Thus the

weighting function of

near the electrodes will cause the flow in that part of the pipe

to have twice the influence on the signal. If all the flow went past that point, and the

flow everywhere else was stationary, the signal would be twice as big as it should be.

This important concept has been extended by Bevir (1970) and Hemp (1975)

and has proved a very useful method of assessing the performance of this and other

types of flowmeter.

However, Figure 12.4 compares the distribution due to Shercliff with others.

Figure 12.4(b) shows the distribution for flowmeters with rectangular-shaped coils, a

common design. Figure 12.4(c) shows the distribution for flowmeters with diamond-

shaped coils with their corners along the axis of the pipe and toward the electrodes.

These are quite similar to some commercial designs, and the plots of weighting

functions can be seen to give a much more uniform distribution, particularly in the

diamond-shaped case.

Another approach that has been used is to introduce large electrodes that have

an integrating effect on the signal and again improve the theoretical performance.

Figure 12.4(d) shows an example of a large electrode meter, and it can be seen that

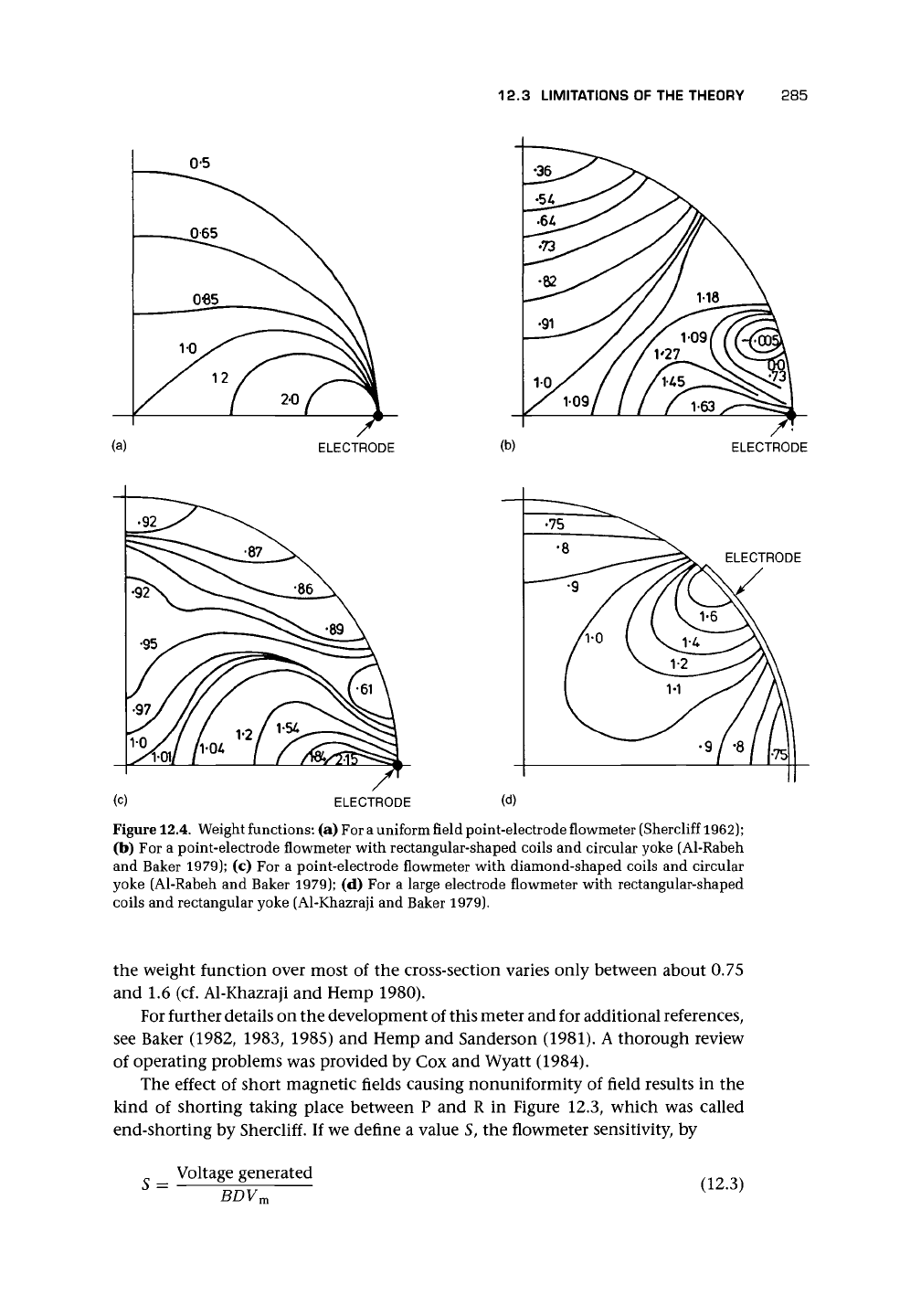
12.3 LIMITATIONS OF THE THEORY

285

ELECTRODE

(d)

Figure

12.4.

Weight functions: (a) For

uniform field point-electrode flowmeter (Shercliff

1962);

(b) For a point-electrode flowmeter with rectangular-shaped coils and circular yoke (Al-Rabeh

and Baker 1979); (c) For a point-electrode flowmeter with diamond-shaped coils and circular

yoke (Al-Rabeh and Baker 1979); (d) For a large electrode flowmeter with rectangular-shaped

coils and rectangular yoke (Al-Khazraji and Baker 1979).

the weight function over most of the cross-section varies only between about 0.75

and 1.6 (cf. Al-Khazraji and Hemp 1980).

For further details on the development of this meter and for additional references,

see Baker (1982, 1983, 1985) and Hemp and Sanderson (1981). A thorough review

of operating problems was provided by Cox and Wyatt (1984).

The effect of short magnetic fields causing nonuniformity of field results in the

kind of shorting taking place between P and R in Figure 12.3, which was called

end-shorting by

Shercliff.

If we define a value S, the flowmeter sensitivity, by

S =

Voltage generated

BDV

(12.3)

286

ELECTROMAGNETIC FLOWMETERS

we find that 5 =

for Equation (12.2), but for a field length equal to the pipe

diameter, it falls to about 0.8.

12.4 DESIGN DETAILS

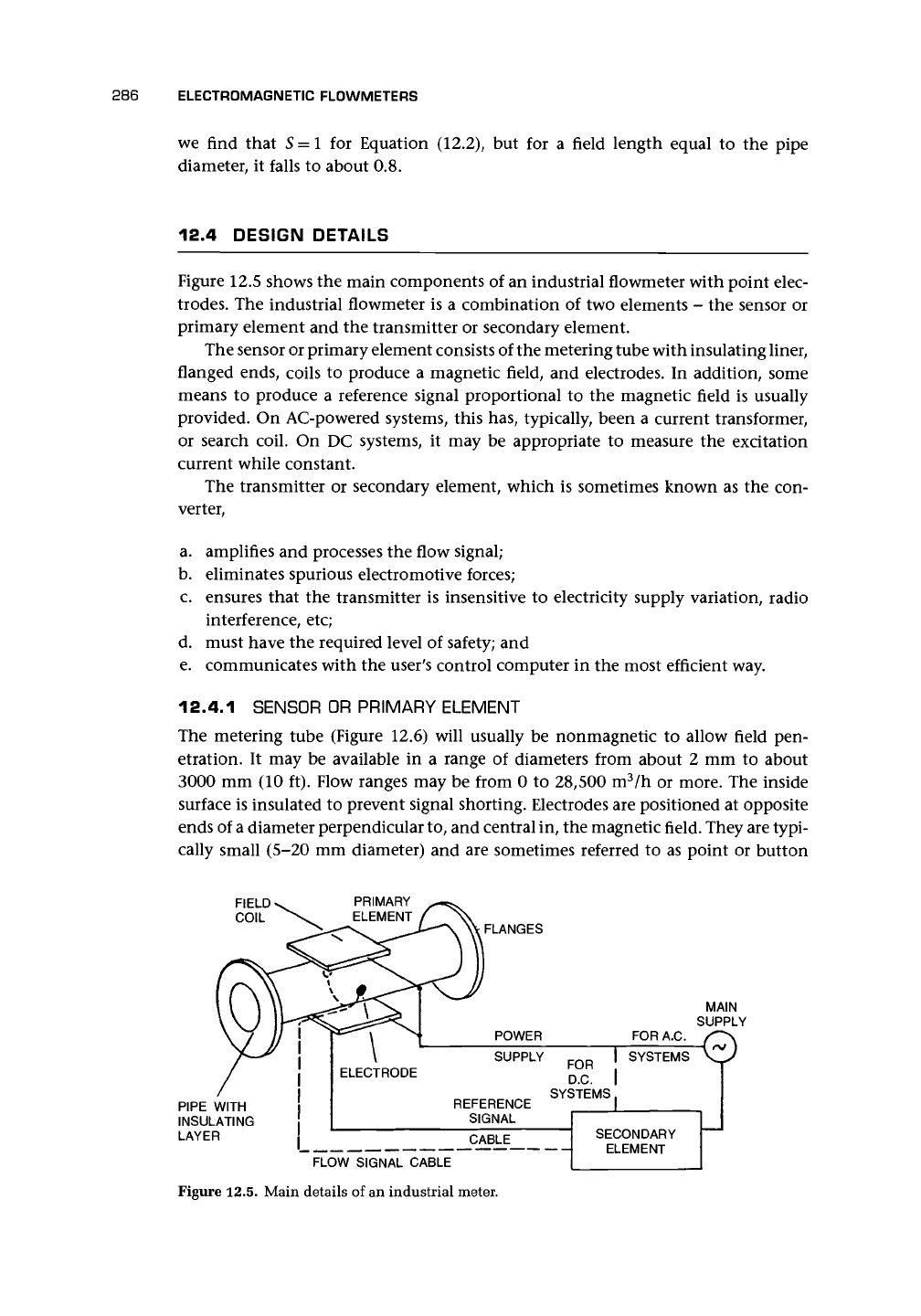
Figure 12.5 shows the main components of an industrial flowmeter with point elec-

trodes. The industrial flowmeter is a combination of two elements - the sensor or

primary element and the transmitter or secondary element.

The sensor or primary element consists of the metering tube with insulating liner,

flanged

ends,

coils to produce a magnetic field, and electrodes. In addition, some

means to produce a reference signal proportional to the magnetic field is usually

provided. On AC-powered systems, this has, typically, been a current transformer,

or search coil. On DC systems, it may be appropriate to measure the excitation

current while constant.

The transmitter or secondary element, which is sometimes known as the con-

verter,

a. amplifies and processes the flow signal;

eliminates spurious electromotive forces;

c. ensures that the transmitter is insensitive to electricity supply variation, radio

interference, etc;

d. must have the required level of safety; and

e. communicates with the user's control computer in the most efficient way.

12.4.1 SENSOR OR PRIMARY ELEMENT

The metering tube (Figure 12.6) will usually be nonmagnetic to allow field pen-

etration. It may be available in a range of diameters from about 2 mm to about

3000 mm (10 ft). Flow ranges may be from 0 to 28,500 m

/h or more. The inside

surface is insulated to prevent signal shorting. Electrodes are positioned at opposite

ends of a diameter perpendicular to, and central in, the magnetic field. They are typi-

cally small (5-20 mm diameter) and are sometimes referred to as point or button

FIELD.

COIL

PRIMARY

ELEMENT

FLOW SIGNAL CABLE

Figure 12.5. Main details of an industrial meter.