Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.


The roots of this equation are
(d)
where v
n2
and m
r
are defined in Eqs. (7.41). From Eqs. (b), the corresponding
mode shape ratios are
(e)
The first mode shape, which corresponds to v
1
0, is a rigid-body mode; that
is, one in which there is no relative displacement between the two masses. The
second mode shape, which corresponds to v
2
, indicates that the displace-
ments of the two masses are always out of phase; that is, when m
1
moves in
one direction, m
2
moves in the opposite direction.
In general, the presence of a rigid-body mode is determined by examin-
ing the stiffness matrix . If the size of the square matrix is n and the rank
of the matrix is m, then there are (n m) zero eigenvalues and, correspond-
ingly, (n m) rigid-body modes.
20
EXAMPLE 7.14 Natural frequencies and mode shapes of
a two-mass-three-spring system
For the system shown in Figure 7.1, let m
1
1.2 kg, m
2
2.7 kg, k
1
10 N/m, k
2
20 N/m, and k
3
15 N/m. This example is identical in spirit to
Example 7.12, except that we will use the nondimensional quantities in car-
rying out the computations. We shall find the natural frequencies and mode
shapes of this system and illustrate how the mode shapes are graphically il-
lustrated. The modal matrix is also constructed.
First, we compute the quantities
rad/s, rad/s,
(a)
From Eqs. (a) and (7.46), we find that
(b)a
2
31 0.75 11 2.25 0.943
2
24 0.943
2
2.889
a
1
1 11 2.25 0.752 0.943
2
4.556
v
r
2.722
2.887
0.943,
m
r
2.7
1.2
2.25,
and
k
32
15
20
0.75
v
n2
A
20
2.7
2.722v
n1
A
10
1.2
2.887
3K 4
X
12
X
22
k
2
k
2
v
2
2
m
1
k
2
k
2
v
n2
2
m
1
11 m
r
2
1
1 11 m
r
2/m
r
m
r
X
11
X
21
k
2
k
2
v
1
2
m
1
1
v
2
v
n2
11 m
r
v
1
0
380 CHAPTER 7 Multiple Degree-of-Freedom Systems
20
E. B. Magrab et al., ibid., Chapter 9.

Making use of Eqs. (b) and Eqs. (7.47), we obtain the nondimensional natu-
ral frequency ratios
(c)
Noting that the natural frequencies v
j
v
n1
j
, we find from Eqs. (a) and (c) that
rad/s
rad/s (d)
Next, the mode shape ratios are computed from Eqs. (7.49), (a), and (c) to be
(e)
After choosing the normalization given by Eqs. (7.30), we set X
2j
1 and
construct the modal matrix as
(f)
We see that for oscillations in the first mode, both masses move in the
same direction, with m
1
moving an amount that is 0.893 times that of m
2
. For
oscillation in the second mode, the masses move in opposite directions, with
m
1
moving 2.518 times as far in one direction as m
2
moves in the opposite di-
rection. It is common, as seen in this example, that the mode shape ratios are
positive in the first mode, and there is a sign change when we go to the sec-
ond mode. The modes {X}
1
and {X}
2
are illustrated in Figure 7.16.
3£ 4 c
0.893 2.518
11
d
X
12
X
22
2.25 0.943
2
1 2.25 0.943
2
1.948
2
2.518
X
11
X
21
2.25 0.943
2
1 2.25 0.943
2
0.873
2
0.893
v
2
2.887 1.948 5.623
v
1
2.887 0.873 2.519
2
30.5 14.556 24.556
2
4 2.8892 1.948
1
30.5 14.556 24.556
2
4 2.8892 0.873
7.3 Free Response Characteristics 381
FIGURE 7.16
Mode shapes for system shown in Figure 7.1.
m
1
m
2
m
1
m
2
m
1
m
2
0.893
1.0
1.02.518
First mode at
1
Second mode at
2

EXAMPLE 7.15 Natural frequencies and mode shapes of a pendulum attached
to a translating mass
Consider the system shown in Figure 7.17. We shall derive the governing
equations of motion for small 0u 0and then use these equations to determine
the natural frequencies and mode shapes associated with this system. The
equations of motion are obtained by using Lagrange’s equations. We will also
illustrate how the expressions for the kinetic energy and the potential energy
are appropriately truncated to obtain the linear equations of motion.
Considering the translation of the point mass m, and the rotation of the
rigid bar M, the system kinetic energy is
(a)
and the system potential energy is
(b)
where the datum for computing the potential energy due to gravity loading
has been chosen at the center of mass of the pendulum. For “small” oscilla-
tions about u 0, Taylor-series expansions lead to
(c)cos u 1
u
2
2
sin u u
V
1
2
k1x L sin u 2
2
Mga11 cos u2
T
1
2
mx
#
2
1
2
J
o
u
#
2
382 CHAPTER 7 Multiple Degree-of-Freedom Systems
FIGURE 7.17
System with two degrees of freedom.
k
x
M
a
L
m
i
x
y
z
j
k
o
c.g.
J
o

and the potential energy given by Eq. (b) is approximated as
21
(d)
Making use of Eqs. (a) and (c) in Eqs. (7.7) for q
1
x and q
2
u and recog-
nizing that Q
x
0 and Q
u
0, we obtain
(e)
Comparing Eq. (e) with Eq. (7.22), we substitute a solution of the form
(f)
into Eq. (e), choose l
2
v
2
, and arrive at the following eigenvalue formu-
lation from Eq. (7.38b)
(g)
where v
2
is the eigenvalue and the eigenvector is given by {X
o
o
}
T
.
Introducing the notations
(h)
Eq. (g) is written as
(i)
where {X
o
L
o
}
T
is the eigenvector and
2
is the eigenvalue.
To determine the nontrivial solution of Eq. (i), we obtain a solution to
(j)
Thus, we obtain
(k)
Expanding Eq. (k) results in the characteristic equation
(l)
4
11 v
r
2
2
2
v
r
2
J
r
0
11
2
21v
r
2
2
2 J
r
0
det c
11
2
2 1
J
r
1v
r
2
2
2
d 0
c
11
2
2 1
J
r
1v
r
2
2
2
de
X
o
L®
o
f e
0
0
f
J
r
mL
2
J
o
,
v
v
n1
,
and
v
r
v
n2
v
n1
v
n1
2
k
m
,
v
n2
2
K
o
J
o
,
K
o
kL
2
Mga
v
2
c
m 0
0 J
o
de
X
o
®
o
f c
k kL
kL kL
2
Mga
de
X
o
®
o
f e
0
0
f
e
x
u
f e
X
o
®
o
fe
lt
c
m 0
0 J
o
de
x
$
u
$
f c
k kL
kL kL
2
Mga
de
x
u
f e
0
0
f
V
1
2
k1x Lu 2
2
1
2
Mgau
2
7.3 Free Response Characteristics 383
21
For obtaining the linear equations of motion, retaining up to quadratic terms in the functions T
and V is sufficient, as illustrated in this example.
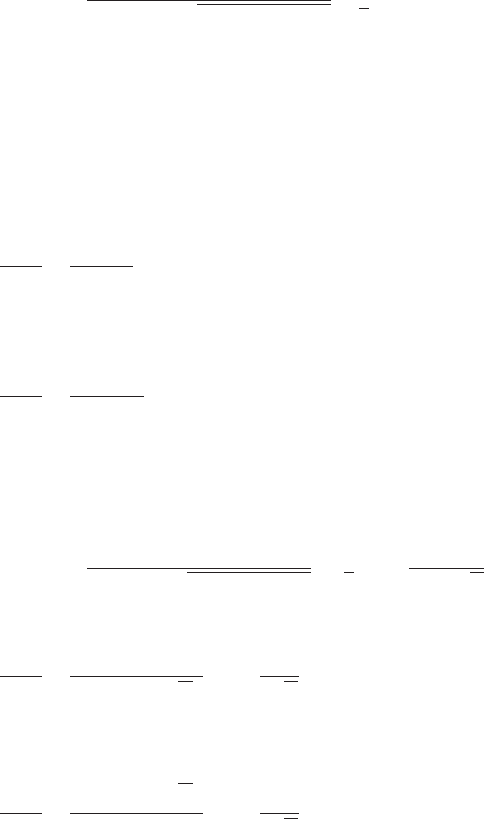
whose roots are
(m)
where the nondimensional natural frequencies have been ordered so that
1
2
. The corresponding mode shapes are obtained from the expanded
form of Eq. (i); that is,
(n)
From the first of Eqs. (n), the mode shape ratio is
(o)
If, instead, we chose the second of Eqs. (n), then the mode shape ratio will
take the form
(p)
Again, the introduction of nondimensional quantities has enabled us to
express the nondimensional frequencies given by Eqs. (m) and the mode
shapes given by Eqs. (o) or (p) in compact form to show the dependence on
the various system parameters.
When v
n1
v
n2
, we see from Eqs. (h) that v
r
1 and Eq. (m) becomes
(q)
and the corresponding mode shape ratios given by Eqs. (o) become
(r)
Alternatively, the mode shape ratios can also be obtained from Eqs. (p); the
result is
(s)
which is identical to Eqs. (r), as expected.
Based on the convention that in the first mode, the mode shape ratios are
positive, the second mode corresponds to the negative sign and the first mode
corresponds to the positive sign. Plots of the two mode shapes are given in
Figure 7.18. We see that for free oscillation in the first mode, the masses move
in the same direction, but with relatively different displacements. In the sec-
ond mode, the masses move in opposite directions. Based on Eqs. (r) and (s),
it is remarked that, although the relative magnitudes of the mode shape dis-
placement components may change as the physical characteristics of a system
change, the directions of the relative motions do not.
X
oj
L®
oj
1 11 2J
r
2
J
r
1
2J
r
for
j 1, 2
X
oj
L®
oj
1
1 11 2J
r
2
1
2J
r
for
j 1, 2
2,1
31 1 211 12
2
4J
r
/ 22 31 2J
r
X
oj
L®
oj
v
r
2
j
2
J
r
for
j 1, 2
X
oj
L®
oj
1
1
j
2
for
j 1, 2
J
r
X
oj
1v
r
2
j
2
2L®
oj
0
for
j 1, 2
11
j
2
2X
oj
L®
oj
0
2,1
31 v
r
2
211 v
r
2
2
2
4J
r
/ 12
384 CHAPTER 7 Multiple Degree-of-Freedom Systems
EXAMPLE 7.16 Natural frequencies and mode shapes of a system with bounce
and pitch motions
We now return to Example 7.3, where we determined the equations govern-
ing the system shown in Figure 7.5. To determine the natural frequencies and
mode shapes of the undamped system, we set c
1
c
2
0 in Eq. (k) of Ex-
ample 7.3. In addition, we shall introduce the notion of a node of a mode
shape. We first introduce the quantities
(a)
Then the eigenvalue formulation obtained from Eq. (k) of Example 7.3 in
expanded form is
(b)
where
2
is the eigenvalue and {YX}
T
is the associated mode shape. Note that
X L
1
is the displacement of the left end of the bar associated with the ro-
tation .
Setting the determinant of the coefficient matrix in Eqs. (b) to zero gives
the following characteristic equation
(c)
where the coefficients in the quartic polynomial are
(d)b
3
k
21
11 L
21
2
2
b
2
1 b
1
11 k
21
v
2
r
2
b
1
k
21
L
2
21
v
2
r
b
1
4
b
2
2
b
3
0
11 k
21
L
21
2Y a
2
k
21
L
2
21
v
2
r
1 k
21
L
2
21
bX 0
1
2
1 k
21
2Y 11 k
21
L
21
2X 0
k
21
k
2
k
1
,
L
21
L
2
L
1
,
and
v
v
n1
X L
1
®,
v
2
r
v
2
n2
v
2
n1
,
v
2
n1
k
1
m
,
v
2
n2
k
2
L
2
2
J
G
7.3 Free Response Characteristics 385
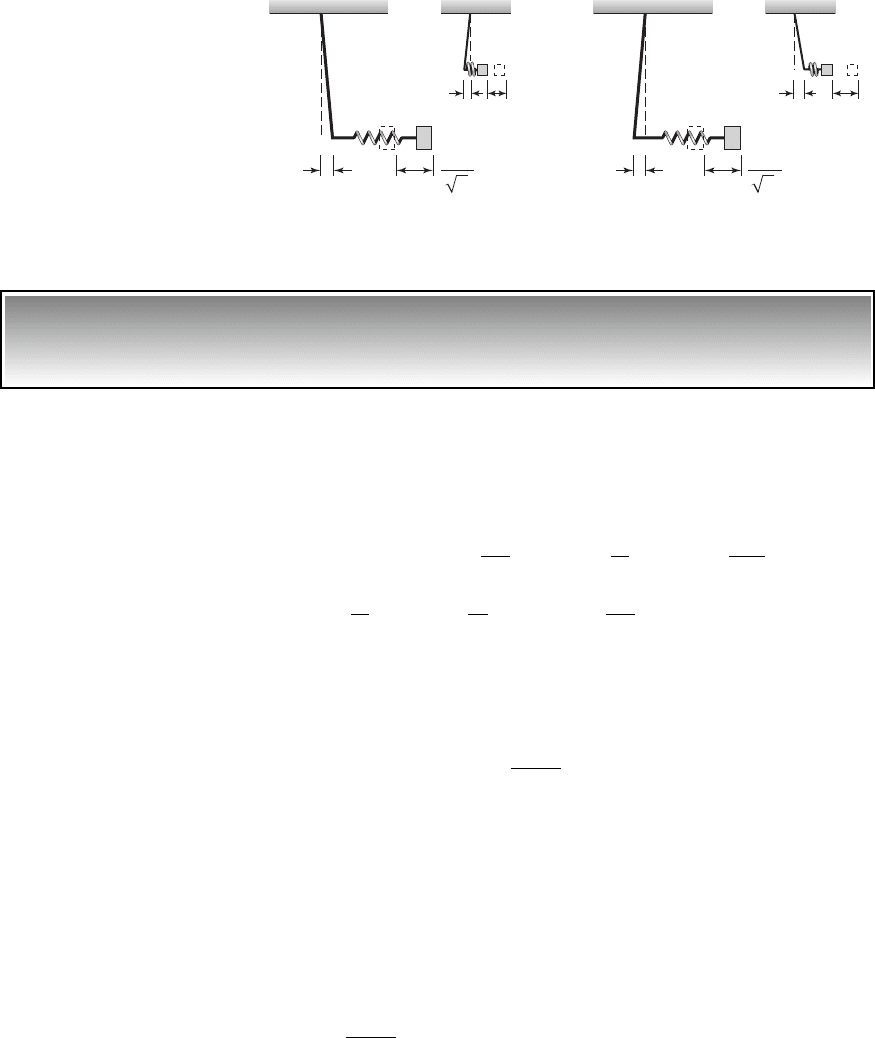
FIGURE 7.18
Mode shapes for the system shown in Figure 7.17 when v
r
1.
First mode
at
1
Second mode
at
2
L
o1
L
o1
L
o2
J
r
L
o2
J
r

The solutions of Eq. (c) provide the nondimensional natural frequencies
(e)
where
1
2
. The mode shapes are obtained from either the first of Eqs.
(b) as
(f)
or from the second of Eqs. (b) as
(g)
We notice that when the ratios k
21
L
21
1; that is, when the spring con-
stants are equal and the center of gravity is midway between both ends, the
system equations are uncoupled as seen from Eqs. (b). In this case, from Eqs.
(b), we obtain
indicating that the rotation is independent of the translation. Thus, in this
special case, if the bar is subjected to a force at its center of gravity, then the
system can only translate. The translation occurs at the nondimensional fre-
quency , or equivalently, at the dimensional frequency v
nt
v
n1
.
In order to illustrate the mode shapes, a numerical case is considered
next. Thus, for the choice, k
21
0.6, L
21
1.1, and v
r
1.32, we find from
Eqs. (d) that b
1
0.417, b
2
2.393, and b
3
2.646. Upon substituting these
values into Eqs. (e), we find that
1
1.223 and
2
2.061. From Eqs. (f),
the respective mode shape ratios are
(h)
Thus, for oscillation in the first mode, we see from Eqs. (h) that if we assume
that there is a displacement d in the negative y-direction at the left end of the
bar, the amount of positive rotation of the bar is d/L
1
about the center of
gravity. In addition, the center of gravity of the bar moves a distance that is
Y
2
X
2
1 0.6 1.1
2.061
2
1 0.6
0.128
Y
1
X
1
1 0.6 1.1
1.223
2
1 0.6
3.261
12k
1
/
m
12
1
2
2
a
2
v
2
r
2 bX 0
1
2
22Y 0
Y
j
X
j
1
1 k
21
L
21
a
2
k
21
L
2
21
v
2
r
1 k
21
L
2
21
b
for
j 1, 2
Y
j
X
j
1 k
21
L
21
j
2
1 k
21
for
j 1, 2
1,2
C
b
2
2b
2
2
4b
1
b
3
2b
1
386 CHAPTER 7 Multiple Degree-of-Freedom Systems

3.261d in the opposite (positive, in this case) direction. The mode shapes
given by Eqs. (h) are shown in Figure 7.19. It is pointed out that there is a
point in each mode shape at which the bar (or an extension of it) intersects the
reference (equilibrium) position. This point does not undergo any motion.
Such a point is called a node point. For the first mode shape, the node point
does not physically lie on the bar. Even so, one can consider this node point
as being the fulcrum for the motion of the rigid bar at its first natural fre-
quency. In other words, the bar oscillates through an arc as if it were pivoted
at that point. For the second mode shape, the node point lies in the span of the
bar. When the bar is vibrating in the second natural frequency, the bar is piv-
oting about this stationary point.
Nodes in vibratory systems play a significant role in determining the
placement of vibration sensors and vibration actuators. For instance, a sensor
placed at the node of a certain mode will not detect that particular mode. Sim-
ilarly, an actuator placed at the node of a certain mode cannot excite that
mode. The observation that when oscillating in a certain mode shape, the dis-
placement is zero at the node point of a mode leads to the following design
guideline.
7.3 Free Response Characteristics 387
FIGURE 7.19
Modes shapes and node points for the system shown in Figure 7.5: k
21
0.6, L
21
1.1, and
v
r
1.32. [Note: Figure not to scale.]
L
1
L
2
c.g.
Node
point
Node
point
Y
1
3.261L
1
1
Y
2
0.128L
1
2
L
1
2
L
1
1
First mode at
1
1.223
Second mode a
t
2
2.061
Design Guideline. For a system with two or more degrees of free-
dom, if a sensor needs to be located so as not to pick up vibrations of a
certain mode, one should locate the sensor at the node point of this
mode. Alternatively, if a sensor should sense vibrations in a certain
mode, one should not locate it at a node of the mode of interest.

EXAMPLE 7.17 Inverse problem: determination of system parameters
Consider the system shown in Figure 7.1, which is described by the follow-
ing inertia matrix and stiffness matrix
N/m (a)
The modes of the system are given by
(b)
and the natural frequency v
1
associated with mode {X}
1
is 100 rad/s. We shall
illustrate how the unknown elements in the stiffness matrix and the other nat-
ural frequency v
2
is determined.
To determine the needed quantities, we make use of Eq. (7.38b). Com-
paring the elements in the given stiffness matrix with that used in Eq. (7.38b),
we determine that
(c)
Therefore, from the first of Eq. (7.40) and Eqs. (b), the mode shape ratio is
(d)
Upon substituting the known numerical values into Eq. (d), we obtain
N/m (e)
From the second of Eq. (7.40), we see that
(f)
From Eq. (f ), we find that
N/m (g)
The other natural frequency is found by making use of the eigenvector
{X}
2
and the first of Eq. (7.40) with j 2. Thus,
(h)
X
22
X
12
k
11
m
1
v
2
2
k
12
1
1/2
2
k
22
3k
12
m
2
v
2
1
3 115,000 2 3 100
2
75,000
X
21
X
11
k
2
k
2
k
3
m
2
v
2
1
k
12
k
22
m
2
v
2
1
1
3
k
12
3 125,000 2 100
2
215,000
X
21
X
11
k
1
k
2
m
1
v
2
1
k
2
k
11
m
1
v
2
1
k
12
1
3
k
22
k
2
k
3
k
12
k
21
k
2
k
11
k
1
k
2
25,000
5X6
1
e
3
1
f
and
5X6
2
e
1/2
1
f
3M 4 c
20
03
d kg
and
3K 4 c
25,000 k
12
k
21
k
22
d
3K 43M4
388 CHAPTER 7 Multiple Degree-of-Freedom Systems
Solving Eq. (h) for v
2
, we obtain
rad/s
EXAMPLE 7.18
Natural frequencies of an N degree-of-freedom system: special case
22
Consider the N degree-of-freedom system given by Eqs. (7.5). If we assume
that c
i
Q
i
0, k
i
k, m
i
m, and use x
i
instead of q
i
, then Eq. (7.5a) becomes
(a)
where, because of the fixed ends, x
0
x
N1
0. To determine the natural fre-
quencies, we let
(b)
Upon substituting Eqs. (b) into Eqs. (a), we arrive at
(c)
where
(d)
Equation (c) is a difference equation whose solution can be obtained in a
manner similar to that of a differential equation. We first assume a solution of
the form
(e)
where b is unknown. Upon substituting Eq. (e) into Eq. (c), we obtain
which leads to
or
(f)
Once b is determined, the natural frequency coefficient can be obtained
from Eq. (f). To determine b, we assume a solution to Eq. (c) of the form
(g)X
n
A cos1nb2 B sin1nb2
n 1,2, . . ., N
2
211 cos b2 4sin
2
1b/2 2
12
2
2 e
jb
e
jb
2 cos b
12
2
2e
jbn
e
jb1n12
e
jb1n12
0
X
n
e
jbn
n 1, 2, . . ., N
v
v
o
and
v
o
B
k
m
12
2
2X
n
X
n1
X
n1
0
n 1, 2, . . ., N
x
n
X
n
e
jvt
n 1, 2, . . ., N
mx
$
n
2kx
n
kx
n1
kx
n1
0
n 1, 2, . . ., N
165.83
v
2
B
1
m
1
ak
12
X
22
X
12
k
11
b
B
1
2
1115,0002 12 2 25,0002
7.3 Free Response Characteristics 389
22
W. T. Thomson, Vibration Theory and Applications, Prentice Hall, Saddle River, NJ, 1965,
pp. 251–253.
