Balakumar Balachandran, Magrab E.B. Vibrations
Подождите немного. Документ загружается.

On substituting Eq. (7.23a) into Eq. (7.22), we obtain
(7.24)
Eigenvalue Problem
Since Eq. (7.24) should be satisfied for all time, we find that
(7.25)
The system of Eq. (7.25) is a system of N linear algebraic equations. This sys-
tem is satisfied for X
1
X
2
. . . X
N
0, which is a trivial solution. Since
we seek nontrivial solutions for X
1
, X
2
, . . ., X
N
, Eq. (7.25) represents an eigen-
value problem.
16
The unknowns are l
2
, X
1
, X
2
, . . ., X
N
, and since there are only
N equations to solve for these (N 1) unknowns, at best, what one could do
is solve for l
2
, and the ratios X
2
/X
1
, X
3
/X
1
, . . ., X
N
/X
1
. The quantity l
2
is re-
ferred to as the eigenvalue and the vector {X
1
X
2
. . . X
N
}
T
is called the eigen-
vector. The eigenvalues l
2
are determined by finding the roots of the charac-
teristic equation
(7.26)
Since the stiffness and mass matrices are NN matrices, the expansion of
Eq. (7.26) is a polynomial of degree 2N in l for an N degree-of-freedom sys-
tem. Alternatively, one can view this polynomial as an Nth order polynomial
in l
2
with N roots or eigenvalues l
2
1
, l
2
2
, . . ., l
2
N
. The associated eigenvectors
are solutions of the equations
(7.27)
where {X}
j
is the eigenvector associated with the eigenvalue l
2
j
and we have
a total of N eigenvectors.
To solve for the eigenvectors associated with the first eigenvalue l
2
1
, the
second eigenvalue l
2
2
, and so forth, we construct the eigenvectors
(7.28a)
which can be written as
5X6
1
X
11
d
1
X
21
/X
11
o
X
N1
/X
11
t,
5X6
2
X
12
d
1
X
22
/X
12
o
X
N2
/X
12
t,
. . .
5X6
1
d
X
11
X
21
o
X
N1
t,
5X6
2
d
X
12
X
22
o
X
N2
t,
. . .
5X6
N
d
X
1N
X
2N
o
X
NN
t
33K 4 l
2
j
3M 445X6
j
506
det33K4 l
2
3M 44 0
33K 4 l
2
3M 445X6 506
33K 4 l
2
3M 445X6e
lt
506
370 CHAPTER 7 Multiple Degree-of-Freedom Systems
16
In general, for a system the problem of finding the constants l for which
the vector {X} is nontrivial, is called an eigenvalue or characteristic value problem. A scalar ver-
sion of this problem was discussed for single degree-of-freedom systems in Section 4.3.
3A 45X6 l¿ 3B 45X6,
(7.28b)
In writing Eqs. (7.28b), it has been assumed that X
1j
0 for j 1, 2, . . ., N.
In Eqs. (7.28), {X}
1
, which is associated with the eigenvalue l
2
1
, is called the
first eigenvector, first eigenmode, or first mode shape, and {X}
2
, which is asso-
ciated with the eigenvalue l
2
2
, is called the second eigenvector, second eigen-
mode, or second mode shape, and so on.
Due to the nature of the eigenvalue problem, the eigenvectors {X}
j
are
arbitrary to a non-zero scaling constant. A convenient normalization that is
often used to remove this arbitrariness is
(7.29)
Another choice for normalization is
(7.30)
and so forth. Physically, the eigenvectors provide information about the rela-
tive spatial positions of the different inertial elements in terms of the general-
ized coordinates. Thus, for free oscillation at l
j
, each mass m
j
moves a fixed
amount relative to m
k
. The process of normalizing the mode shapes (eigen-
vectors) of a system is called normalization, and the resulting modes are
called normal modes.
The mode shapes are placed in a modal matrix , which is
(7.31)
where {X}
j
is the mode shape associated with the jth eigenvalue l
2
j
. When the
normalization of the mode shapes is carried out according to Eqs. (7.29), then
the modal matrix takes the form
(7.32)
When the normalization is carried out according to Eqs. (7.30), then the
modal matrix takes the form
(7.33)3£ 4 D
X
11
/X
21
X
12
/X
22
p
X
1N
/X
2N
11
p
1
oo
p
o
X
N1
/X
21
X
N2
/X
22
p
X
NN
/X
2N
T
3£ 4 D
11
p
1
X
21
/X
11
X
22
/X
12
p
X
2N
/X
1N
oo
p
o
X
N1
/X
11
X
N2
/X
12
p
X
NN
/X
1N
T
3£ 4 55X6
1
5X6
2
p
5X6
N
6 D
X
11
X
12
p
X
1N
X
21
X
22
p
X
2N
oo∞o
X
N1
X
N2
p
X
NN
T
3£ 4
X
21
1,
X
22
1,
. . .,
X
2N
1
X
11
1,
X
12
1,
. . .,
X
1N
1
5X6
N
X
1N
d
1
X
2N
/X
1N
o
X
NN
/X
1N
t
7.3 Free Response Characteristics 371

and so forth. When the eigenvectors are normalized so that their magnitude is
one, the corresponding normalization equation is
(7.34)
However, regardless of the choice of the normalization, the ratios of the dif-
ferent components in an eigenvector are always preserved.
For real and symmetric matrices and , the eigenvalues l
2
of
Eq. (7.25) are real and the associated eigenvectors {X}
j
are also real.
17
Hence,
it is common to write
(7.35)
where v is a positive quantity. It will be shown later to be one of the N natu-
ral frequencies of the N degree-of-freedom system. On substituting for l
2
from Eq. (7.35) into Eqs. (7.26) and (7.27), we find that the natural frequen-
cies are determined by solving the characteristic equation
(7.36)
which is an Nth order polynomial in v
2
and that the eigenvectors {X}
j
associ-
ated with the natural frequencies v
j
are determined from
(7.37)
For a system with N degrees of freedom, Eq. (7.36) provides the N natural fre-
quencies v
1
, v
2
, . . ., v
N
and Eq. (7.37) provides the associated eigenvectors
{X}
1
,{X}
2
, . . ., {X}
N
. The natural frequencies are ordered so that
Hence, the first natural frequency is lower than or equal to the second natural
frequency, and so forth. It is noted that this ordering should not be expected
when software such as MATLAB is used to solve Eq. (7.36).
To illustrate how the eigenvalues and eigenvectors are determined for a
multi-degree-of-freedom system, we use two degree-of-freedom systems.
However, the discussion provided below is valid for any linear multi-degree-
of-freedom system.
Free Oscillations of Two Degree-of-Freedom Systems
Setting N 2 in Eq. (7.37), and using the definitions of and from
Eqs. (7.5b), we obtain
(7.38a)
which is rewritten as
(7.38b)c
k
1
k
2
v
2
m
1
k
2
k
2
k
2
k
3
v
2
m
2
de
X
1
X
2
f e
0
0
f
cv
2
c
m
1
0
0 m
2
d c
k
1
k
2
k
2
k
2
k
2
k
3
dde
X
1
X
2
f e
0
0
f
3M 43K 4
v
1
v
2
. . . v
N
33K 4 v
2
j
3M 445X6
j
506
det33K4 v
2
3M 44 0
l
2
1jv 2
2
v
2
3K 43M 4
‘ 5X6
j
‘ 2X
1j
2
X
2j
2
###
X
Nj
2
1
372 CHAPTER 7 Multiple Degree-of-Freedom Systems
17
For a comprehensive discussion of eigenvalue problems associated with structural and
mechanical systems, see L. Meirovitch, ibid.

In this case, the characteristic equation given by Eq. (7.36) translates to
(7.39a)
which, when expanded, takes the form
(7.39b)
Equation (7.39b) is rewritten as
(7.39c)
which is a fourth-order polynomial in v. Due to the form of this equation, one
can treat it as a quadratic polynomial in v
2
. From Eq. (7.37), the eigenvectors
associated with the natural frequencies v
1
and v
2
are determined from the fol-
lowing system of equations:
(7.40)
Next, we present an example to show the explicit details of determining
the natural frequencies and mode shapes of a two degree-of-freedom system
before examining a nondimensional form of the system given by Eq. (7.38a).
The nondimensional form is better suited for examining the influences of the
different parameters on the system natural frequencies and mode shapes.
EXAMPLE 7.12
Natural frequencies and mode shapes of
a two degree-of-freedom system
We shall illustrate how the algebraic system given by Eq. (7.38b) is solved to
determine the natural frequencies and mode shapes associated with a specific
two degree-of-freedom system. The modal matrix of the system is also
constructed. We choose the stiffness parameters k
1
, k
2
, and k
3
and the mass pa-
rameters m
1
and m
2
so that
(a)
Thus, making use of Eqs. (a) in Eq. (7.38b), we obtain
(b)
To determine the natural frequencies of the system, we make use of Eq. (7.36)
and Eqs. (a) to arrive at
(c)det c
2k v
2
m k
k 2k v
2
m
d 0
c
2k v
2
m k
k 2k v
2
m
de
X
1
X
2
f e
0
0
f
k
1
k
2
k
3
k
and
m
1
m
2
m
3£ 4
c
k
1
k
2
v
2
j
m
1
k
2
k
2
k
2
k
3
v
j
2
m
2
de
X
1j
X
2j
f e
0
0
f
j 1, 2
m
1
m
2
v
4
31k
1
k
2
2m
2
1k
2
k
3
2m
1
4v
2
1k
1
k
2
21k
2
k
3
2 k
2
2
0
1k
1
k
2
v
2
m
1
21k
2
k
3
v
2
m
2
2 k
2
2
0
det c
k
1
k
2
v
2
m
1
k
2
k
2
k
2
k
3
v
2
m
2
d 0
7.3 Free Response Characteristics 373

On expanding Eq. (c), the result is the characteristic equation
which yields
(e)
Thus, the two roots are given by
and (f)
which are the two natural frequencies of the system and they have been or-
dered so that v
1
v
2
.
To determine the associated mode shapes, we make use of Eqs. (7.40),
(b), and (f). Therefore, to determine the mode shape associated with v
1
,we
set v v
1
in Eq. (b) to obtain
which, upon using the first of Eqs. (f), reduces to
(g)
From the first of Eq. (g), we find that
or
(h)
The second of Eq. (g) also provides the same ratio of modal amplitudes, as
expected. Then, choosing the normalization given by Eq. (7.29), Eqs. (7.28b)
and (h) lead to
(i)
Thus, mass m
1
and mass m
2
move in the same direction with the same
displacement.
To determine the second mode shape associated with v
2
, we set v v
2
in Eqs. (b) to obtain
which, upon using the second of Eqs. (f), reduces to
(j)c
k k
k k
de
X
12
X
22
f e
0
0
f
c
2k v
2
2
m k
k 2k v
2
2
m
de
X
12
X
22
f e
0
0
f
5X6
1
X
11
e
1
1
f
X
21
X
11
1
kX
11
kX
21
0
c
k k
kk
de
X
11
X
21
f e
0
0
f
c
2k v
1
2
m k
k 2k v
1
2
m
de
X
11
X
21
f e
0
0
f
v
2
A
3k
m
v
1
A
k
m
2k v
2
m k
12k v
2
m2
2
k
2
0
374 CHAPTER 7 Multiple Degree-of-Freedom Systems

From the first of Eq. (j) we find that
(k)
Thus, mass m
1
and mass m
2
move in the opposite directions but with the same
displacement.
The ratio of the modal amplitudes shown in Eq. (k) could have also been
determined from the second of Eq. (j). Again choosing the normalization
given by Eq. (7.29), Eqs. (7.28b) and (k) lead to
(l)
For the normalization chosen, the modal matrix is obtained from Eqs.
(7.31), (i), and (l) as
(m)
In Example 7.12, the natural frequencies and mode shapes were deter-
mined for a two degree-of-freedom system with a specific set of parameters.
In order to explore the natural frequencies and mode shapes associated with
arbitrary system parameters, we introduce many nondimensional parameters
and then solve the system given by Eq. (7.38b) in terms of these nondimen-
sional parameters.
Eigenvalue Problem in Terms of Nondimensional Parameters
In order to rewrite Eq. (7.38b) in terms of nondimensional mass, stiffness, and
frequency parameters, we introduce the following quantities:
(7.41)
On substituting the different quantities from Eqs. (7.41) into Eq. (7.38b), we
find that the resulting system is
(7.42a)
which, in matrix form, is
(7.42b)
For the eigenvalue formulation given by Eq. (7.42a) or (7.42b), the eigenvalue
is
2
and the corresponding eigenvector is {X}. This system of equations has
c
1 v
r
2
m
r
2
m
r
v
r
2
v
r
2
v
r
2
11 k
32
2
2
de
X
1
X
2
f e
0
0
f
v
r
2
X
1
3v
r
2
11 k
32
2
2
4X
2
0
31 v
r
2
m
r
2
4X
1
m
r
v
r
2
X
2
0
v
r
v
n2
v
n1
1
1m
r
A
k
2
k
1
,
and
k
32
k
3
k
2
v
nj
2
k
j
m
j
,
j 1, 2
m
r
m
2
m
1
,
v
v
n1
3£ 4 c
11
1 1
d
5X6
2
X
12
e
1
1
f
X
22
X
12
1
7.3 Free Response Characteristics 375
a nontrivial solution for {X} only when the determinant of the coefficient
matrix from Eq. (7.42b) is zero. Thus, from Eqs. (7.42b), we arrive at
(7.43)
which gives the characteristic equation
(7.44)
Equation (7.44) is Eq. (7.39c) rewritten in terms of the nondimensional quan-
tities given by Eqs. (7.41). It is important to note that the nondimensionaliza-
tion introduced in Eqs. (7.41) led to the compact form of the characteristic
equation, Eq. (7.44), which enables one to readily identify the parameters on
which the natural frequencies depend.
Expanding Eq. (7.44) leads to
(7.45)
where
(7.46)
The two positive roots of this characteristic equation given by Eq. (7.45) are
(7.47)
1,2
B
1
2
3a
1
2a
1
2
4a
2
4
a
2
v
r
2
31 k
32
11 v
r
2
m
r
2
a
1
1 v
r
2
11 m
r
k
32
2
4
a
1
2
a
2
0
31 v
r
2
m
r
2
43v
r
2
11 k
32
2
2
4 m
r
v
r
4
0
det c
1 v
r
2
m
r
2
m
r
v
r
v
r
2
v
r
2
11 k
32
2
2
d 0
376 CHAPTER 7 Multiple Degree-of-Freedom Systems
0
0.5
1
1.5
2
0
1
2
3
0
0.5
1
1.5
m
r
v
r
Ω
1
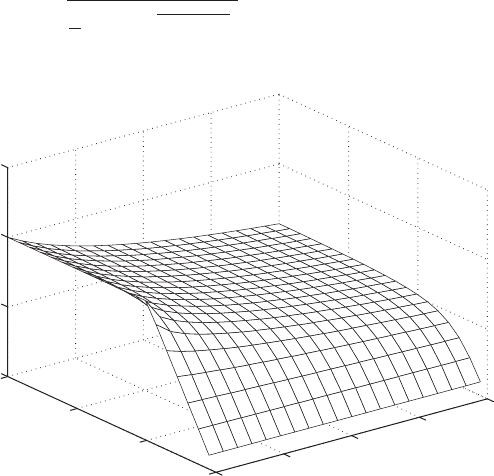
FIGURE 7.13
Variation of the first nondimensional natural frequency of two degree-of-freedom
system shown in Figure 7.1 as a function of m
r
and v
r
when k
3
0.

7.3 Free Response Characteristics 377
18
In practice, when software such as MATLAB is used to determine the eigenvalues of a system
of the form, the eigenvalues obtained are not ordered in terms of magnitude from the lowest to
the highest. See Chapter 9 of E. B. Magrab et al., An Engineer’s Guide to MATLAB, 2nd ed.,
Prentice Hall, Upper Saddle River NJ (2005).
19
We shall continue to include k
3
and c
3
in determining the necessary equations, but when we nu-
merically evaluate related expressions, these coefficients are frequently set to zero.
0
0.5
1
1.5
2
0
1
2
3
0
1
2
3
4
5
6
m
r
v
r
Ω
2
FIGURE 7.14
Variation of the second nondimensional natural frequency of the two degree-of-freedom system
shown in Figure 7.1 as a function of m
r
and v
r
when k
3
0.
and the frequency ratios
1
and
2
are ordered such that
1
2
.
18
The
frequency v
1
associated with
1
is called the first natural frequency and the
frequency v
2
associated with
2
is called the second natural frequency.
We see that when the interconnecting spring k
2
is absent from the system
shown in Figure 7.1, we can set k
2
0(v
r
0) in Eq. (7.39b) and, as expected,
the resulting system is uncoupled. The two natural frequencies are, respec-
tively, the natural frequencies of two independent single degree-of-freedom
systems. One natural frequency is and the other natural fre-
quency is . When k
1
0, k
2
0, and k
3
0, appropriate ex-
pressions are similarly obtained.
19
Based on Eqs. (7.45), (7.46), and (7.41), we see that, in general, the nat-
ural frequencies of this system are functions of the three nondimensional pa-
rameters: m
r
, v
r
, and k
32
. If we assume that k
32
0 (i.e., k
3
0), then we can
graph the first and second natural frequency ratios as functions of m
r
and v
r
.
The results are shown in Figures 7.13 and 7.14, and they lead to the follow-
ing design guideline.
v
n2
2k
3
/m
2
v
n1
2k
1
/m
1

We return to Eqs. (7.42a) and determine the eigenvectors associated with
1
and
2
. For
j
, we have
(7.48)
where X
1j
and X
2j
are the respective displacements of the two masses oscillat-
ing at the frequency v
n1
j
. Since we can solve only for the ratio of X
1j
/X
2j
or
X
2j
/X
1j
, from the first of Eqs. (7.48), we arrive at
(7.49)
and from the second of Eqs. (7.48) we arrive at
(7.50)
Although Eqs. (7.49) and (7.50) appear to have algebraically different
forms, they can be shown to be identical by making use of Eqs. (7.47). It is re-
marked again that the nondimensionalization introduced in Eqs. (7.41) enables
us to determine the dependence of the mode shapes on the various system pa-
rameters, as seen from the compact forms of Eqs. (7.45) through (7.50).
For a special case of interest, we let k
32
0 and m
r
1 for the system
shown in Figure 7.1. Then, Eqs. (7.46) lead to
(7.51)
and the associated natural frequency ratios
j
are determined from Eqs.
(7.47) to be
(7.52)
and
(7.53)
1
2
씮 1
2
2
씮 v
r
2
f
for
v
r
1
1
2
씮 v
r
2
2
2
씮 1
f
for
v
r
1
a
2
씮 v
r
2
a
1
씮 1 v
r
2
X
1j
X
2j
v
r
2
11 k
32
2
j
2
v
r
2
j 1, 2
X
1j
X
2j
m
r
v
r
2
1 v
r
2
m
r
j
2
j 1, 2
v
r
2
X
1j
3v
r
2
11 k
32
2
j
2
4X
2j
0
31 v
r
2
m
r
j
2
4X
1j
m
r
v
r
2
X
2j
0
378 CHAPTER 7 Multiple Degree-of-Freedom Systems
Design Guideline. For a two degree-of-freedom system with two
springs and two masses, as the mass ratio m
r
m
2
/m
1
increases, the first
nondimensional natural frequency
1
decreases and the second nondi-
mensional natural frequency
2
increases. Thus, increasing the ratio of
the two masses tends to drive the two natural frequencies away from
each other. For a constant mass ratio, we see that an increase in the stiff-
ness ratio k
2
/k
1
increases both
1
and
2
.
Substituting these limiting values into Eq. (7.50), we find that the modal ma-
trices in these two regions are as follows. For v
r
1
(7.54a)
and for v
r
1
(7.54b)
The modal matrix plays a key role in determining the response of vibratory
systems. In the next section, properties of mode shapes are examined. In the re-
mainder of this section, we illustrate the determination and interpretation of
natural frequencies and mode shapes through different examples.
EXAMPLE 7.13
Rigid-body mode of a railway car system
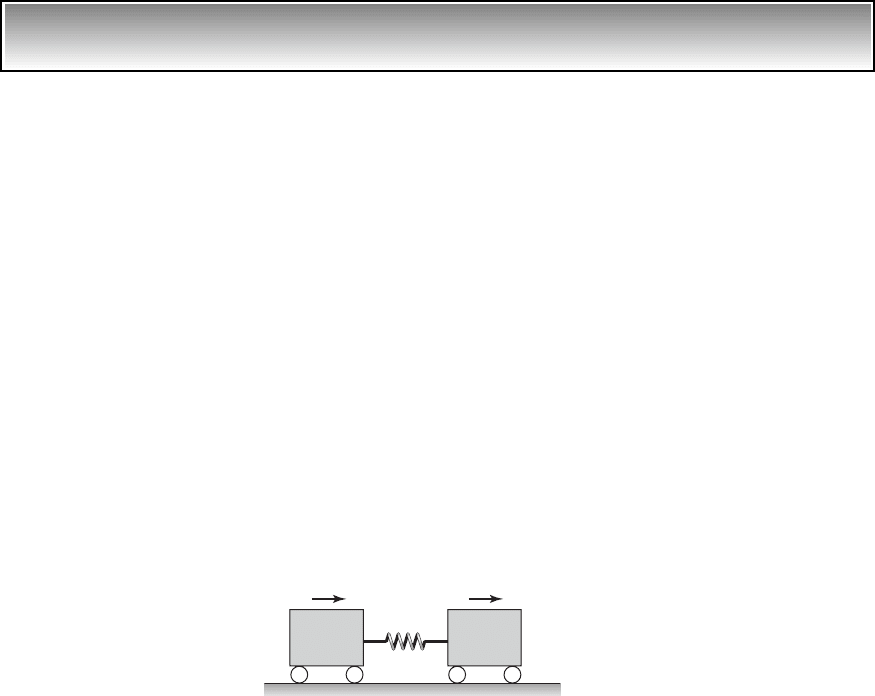
A special case of interest is when
(a)
for the system shown in Figure 7.1; that is, we have two masses connected by
a spring as shown in Figure 7.15. This system is used to model two intercon-
nected railway cars, a truck towing a car, and other such systems. Through
this example, we illustrate what is meant by a rigid-body mode of oscillation.
In this case, Eq. (7.38b) reduces to
(b)
and the characteristic equation given by Eq. (7.39c) simplifies to
(c)
or
v
2
Am
1
m
2
v
2
k
2
1m
1
m
2
2B 0
1k
2
v
2
m
1
21k
2
v
2
m
2
2 k
2
2
0
c
k
2
v
2
m
1
k
2
k
2
k
2
v
2
m
2
de
X
1
X
2
f e
0
0
f
k
1
k
3
c
1
c
2
c
3
0
3£ 4 c
1 1/v
r
2
0
11
d
3£ 4 c
01 1/v
r
2
11
d
7.3 Free Response Characteristics 379
FIGURE 7.15
Two carts with a spring interconnection.
k
2
m
1
m
2
x
1
x
2
