Bhushan B. Handbook of Micro/Nano Tribology, Second Edition
Подождите немного. Документ загружается.


© 1999 by CRC Press LLC
FIGURE 2.38 Variation of the light added to a topography. (a) is the topography without any light (the same as
Figure 2.35). (c) is the same data, but rendered with a light source from the right at 50° elevation. (b) has 20% light
added, (c) 40%, (d) 60%, (e) 80%, and (f) 100%.

© 1999 by CRC Press LLC
Figure 2.40 shows the influence of the elevation angle on the displayed image. It is clear that an
illumination from about 30° to 60° is optimal. One can combine top views or illuminated top views and
wire mesh scan displays to form solid surface models of the sample surface. Such images are usually only
generated in the final processing stage before publication, because they need quite a lot of computing time.
Continuous shading techniques sometimes make it difficult to analyze the topography. By using
discontinuous color tables, one can create something similar to contour maps. An example is shown in
Figure 2.41.
Figure 2.42 shows a combination of the top view display and the wire mesh display, a three-dimensional
model where the height is coded as a shade of gray. As with the top view (Figure 2.35), one can vary the
amount of illumination added to the data. Figures 2.42 through 2.47 show the influence of the amount
of illumination in the display.
Data consisting of more than one channel can be packed into one three-dimensional image. One
channel, usually the topography, is used to model the height, whereas the second channel is used to
produce the shades. Figure 2.48 shows the topography shaded with the stiffness. Figure 2.49 shows the
same data, but colored with the topography.
FIGURE 2.39(a–d)
© 1999 by CRC Press LLC
Additional information can be packed into an image by using color. Assume that an image has two
planes of data. We can display the first plane with shades of green and the second one with shades of red
on top of each other. Where the magnitude of both planes is high, one gets an orange color; where both
are low, one gets black. But if the magnitude of one plane is larger than that of the other plane on one
pixel, one gets red or green colors. This way, one can display the registry of two different quantities in
the same image.
2.9.7 The Two-Dimensional Histogram Method
To analyze quantitatively friction microscopy data, one would like to calculate local friction coefficients.
Normally, one operates a friction microscope in the constant-force mode, recording the topography z(x,y)
and the lateral force F
L
(x,y). If the normal force F
N
is kept constant, one can get a local friction coefficient
γ(x,y) = F
L
(x,y)/F
N
. γ(x,y) is well defined, if the normal force F
N
is truly constant, if the calibrations of
both forces are known, and, most crucially, if the zero points of the force scales are known and stable.
FIGURE 2.39 Illuminated surface: (a) shows an illumination from the top (0°) with an elevation of 50°. (b) is from
45° (upper right) — (b) and all the other illuminations have an elevation of 50°. (c) is at 90°, (d) at 135°, (e) at 180°,
(f) at 225°, (g) at 270°, and (h) at 315°.

© 1999 by CRC Press LLC
In many force microscopes the scales can be calibrated rather accurately, for instance, using the procedure
outlined above, but the zero points are quite unreliable. The zeros usually do not drift very much, but
it is hard to determine their exact position on the force scales.
Figure 2.50 shows the two-dimensional histograms calculated with data from Figure 2.35. These his-
tograms, first used as a data reduction means in communications with satellites (Yaroslavski, 1985), show
correlations between different data channels. In the case of friction data, the lateral force F
L
(x,y) and the
normal force F
N
(x,y) are used as an address to bins arranged in a two-dimensional array (Marti, 1993a,b;
Marti et al., 1993). For every data point (x,y) the bin addressed by (F
N
(x,y), F
L
(x,y)) is incremented by
one. The two-dimensional histogram then shows the statistical weight of every combination. For a
constant friction coefficient and a varying normal force, one obtains (F
N
(x,y), F
L
(x,y)) pairs located on
a straight line, with the slope equal to the friction coefficient. Since the creation of a two-dimensional
histogram is independent of the zero point values, it is not necessary to know the offsets. If different
materials are present on the sample surface and if they have friction coefficients of sufficiently different
magnitudes, then the two materials will fall into different groups of bins in the two-dimensional histo-
gram. Displaying only points falling into one group of bins will select all the locations where one material
is present (Marti 1993a,b; Lüthi et al., 1995; Meyer et al., 1996).
FIGURE 2.40(a–d)

© 1999 by CRC Press LLC
As was shown above, the two-dimensional histogram analysis is not limited to an analysis of friction
force data. It could be applied to other problems in scanning probe microscopy, for instance, relating
spectroscopic data to the tunneling current or to determine the locations of excessive forces or tunneling
currents, to name a few.
2.9.8 Some Common Image-Processing Methods
Since many commercial data acquisition systems use implicitly some kind of data processing, we will
describe some of the effects of these procedures. Since the original data is commonly subject to slopes
on the surface, most programs use some kind of slope correction. Figure 2.51 shows the effect of such
algorithms. In Figure 2.51a there is the original data, without any correction. The least disturbing way
is to subtract a plane z(x,y) = a
x
x + a
y
y + a
0
from the data. The coefficients are determined by fitting
z(x,y) to the data. As can be seen in Figure 2.51b, the main effect is to lower the right side and to lift up
the left side. A more severe option is to subtract a second order function such as ˜z(x,y) = a
xx
x
2
+ a
yy
y
2
+
a
xy
xy + a
x
x + a
y
y + a
0
. Again, the parameters are determined with a fit. This function is appropriate for
FIGURE 2.40 Influence of the elevation angle on the displayed data in illumination mode. The data are illuminated
from the right. (a) has an elevation angle of 0° (from top). (b) is at 15°, (c) at 30°, (d) at 45°, (e) at 60°, (f) at 75°,
and (g) at 90° (parallel to the surface).
© 1999 by CRC Press LLC
FIGURE 2.41 A discontinuous color table can generate a data display similar to contour maps. Here we have used
a color table with 32 steps.
FIGURE 2.42 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is purely topo-
graphical.
© 1999 by CRC Press LLC
FIGURE 2.43 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is 80% topo-
graphical and 20% illumination.
FIGURE 2.44 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is 60% topo-
graphical and 40% illumination.
© 1999 by CRC Press LLC
FIGURE 2.45 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is 40% topo-
graphical and 60% illumination.
FIGURE 2.46 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is 20% topo-
graphical and 80% illumination.
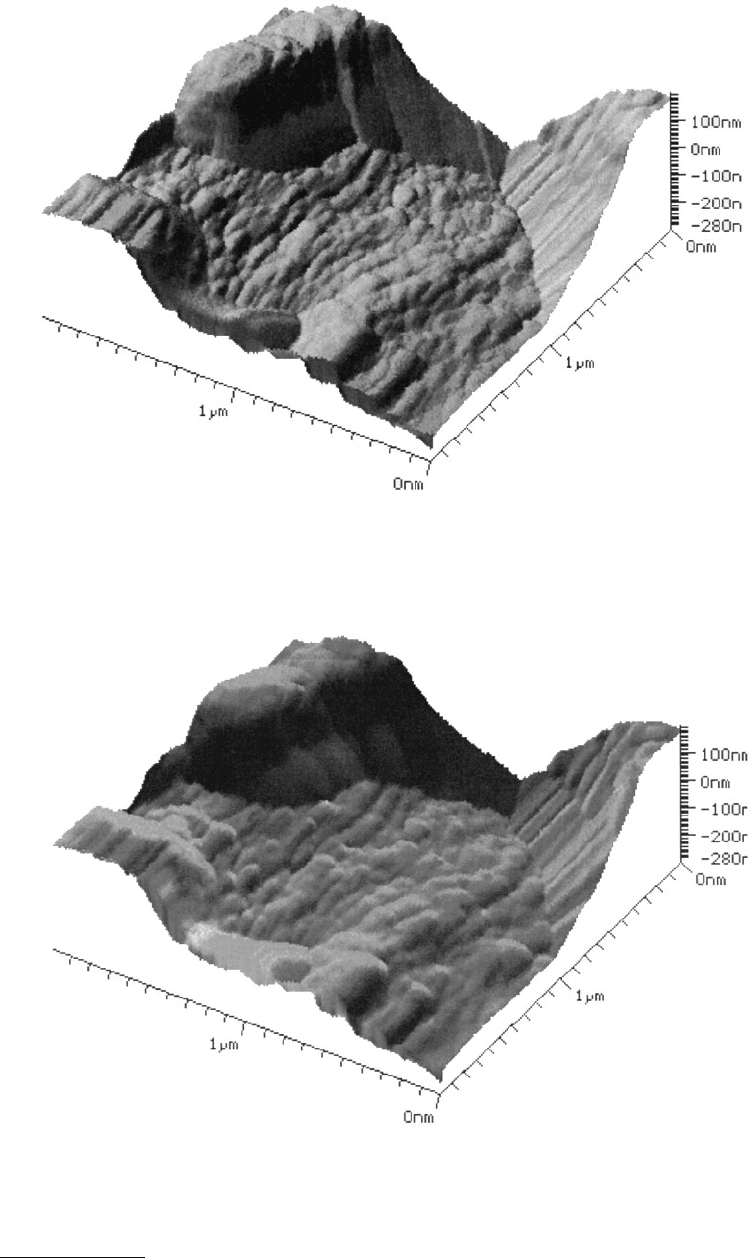
© 1999 by CRC Press LLC
FIGURE 2.47 Three-dimensional rendering of the data of Figure 2.35. The shading of the surface is purely illumi-
nation.
FIGURE 2.48 Three-dimensional rendering of the data of Figure 2.35. The topography channel determines the
height, whereas the stiffness channel gives the color.

© 1999 by CRC Press LLC
almost plane data, where the nonlinearity of the piezos caused such a distortion. It is obvious that the
data are now grossly distorted. Both algorithms have two disadvantages. They can only be used for data
that are already known and they can be calculation intensive.
During data acquisition, only part of the data is known. Therefore, other algorithms which only work
on single rows or columns are preferred. Figure 2.51d shows the effect of subtracting the average of a
row from every point in the row. Data sets that have fine structure and no long-range variations of the
slope can safely be subject to this algorithm. These data, however, are affected and change its character.
Figure 2.51e shows the same procedure, but now applied to the columns. Figure 2.51f is an extension to
subtracting the data. Here not only the average value is subtracted, but also the slope of a line fitted to
one row. Hence, all the tilt is also taken out of the data. This is a dangerous function, since it can
completely change the data appearance. However, most data acquisition programs use exactly this func-
tion. Figure 2.51g, finally, is the same procedure applied to rows.
Figure 2.51h shows the effect of an unsharp mask. This procedure first calculates a low-pass filtered
image by averaging all the points in the neighborhood and then subtracting this value. As can be seen,
the effect is a high-pass filter where all the slow variations are gone. While this technique is ideally suited
to finding out if there are short-range variations in the data.
With data sets such as that in Figure 2.35 where low-lying data are almost not visible, one might be
tempted to apply a technique widely used in image processing: histogram equalization (Figure 2.52).
This technique calculates a cumulative histogram of the z-values. The number as a function of the height
class defines a function. The inverse of this function is then applied to the data. After this operation the
histogram has an equal number of points in the height classes. Since it is a nonlinear function, we do
not recommend that it be used on AFM data.
FIGURE 2.49 Three-dimensional rendering of the data of Figure 2.35. The topography channel determines the
height, whereas the adhesion channel gives the color.
