Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

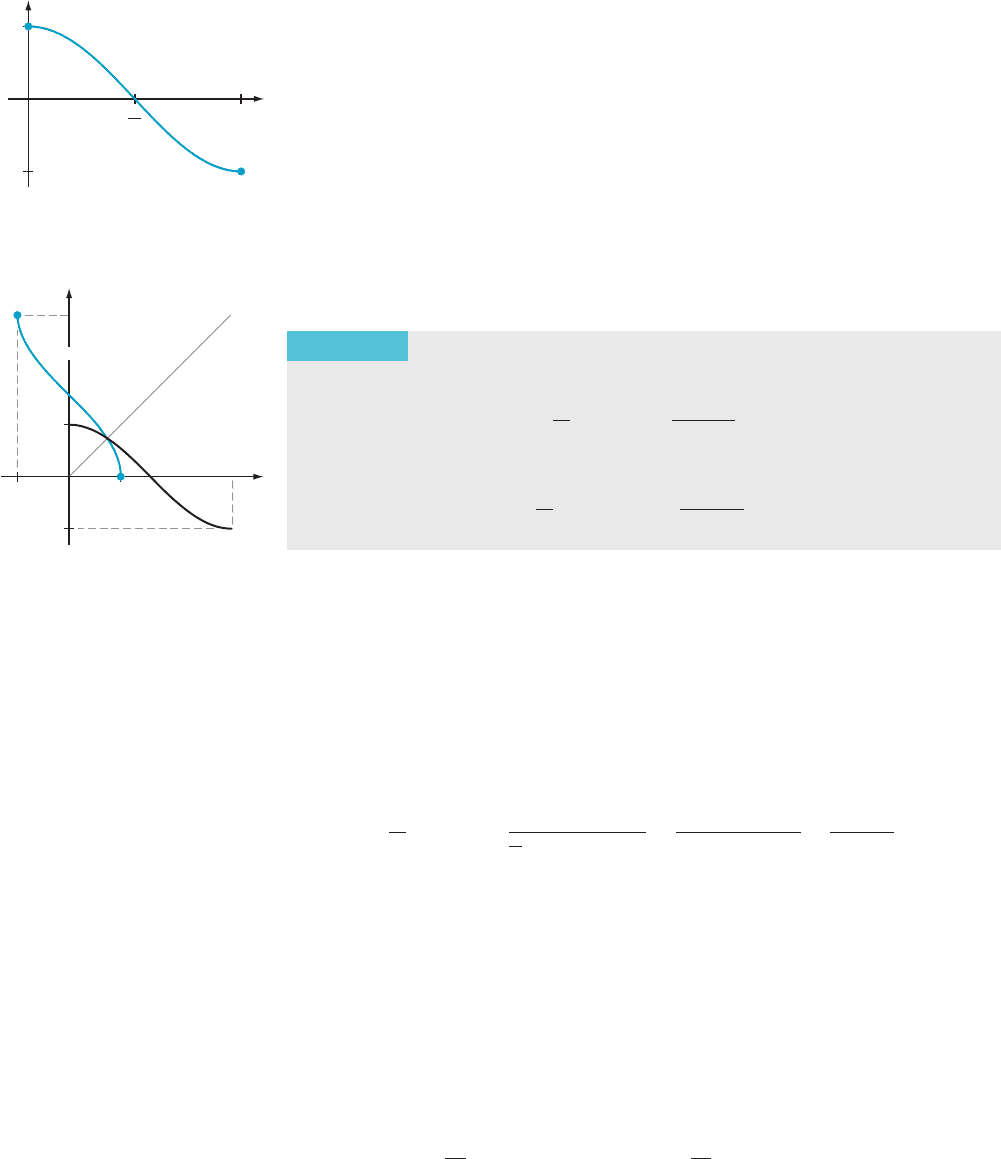
function restricted to the interval [0, π]. Then, as Figure 5 shows, x / Cos(x)isa

one-to-one function. It takes on all the values in the interval [21, 1]. Thus Cos : [0,

π] - [21, 1] is both one-to-one and onto, hence invertible. Its inverse function,

Cos

:[21, 1] - [0, π], is decreasing, one-to-one, and onto. The inverse cosine

x / Cos

(x) is also called the arccosine and denoted by arccos (x ). We reﬂect the

graph of y 5 Cos(x ) in the line y 5 x to obtain the graph of y 5 Cos

(x). The result

is shown in Figure 6.

⁄ EX

AMPLE 2 Calculate arccosð2

ﬃﬃﬃ

=2Þ, arccos (0), and arccosð

ﬃﬃﬃ

=2Þ.

Solution We

calculate as in Example 1 except that here we are looking for values

in the interval [0, π]. We have arccosð2

ﬃﬃﬃ

=2Þ5 3π=4; arccosð0Þ5 π=2, and arccos

ﬃﬃﬃ

=2Þ5 π=6.

THEOREM 1

The functions t / arcsin ( t) and t / arccos (t) are differentiable

on the open interval (21, 1) and

arcsinðtÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 t

ð3:10:1Þ

and

arccosðtÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 t

: ð3:10:2Þ

Proof. For t in

the open interval (21, 1), let s 5 arcsin (t). Then s is in the open

interval (2π/2, π/2) and cos (s) is positive. Using this observation together with the

identity cos

(s) 5 1 2 sin

(s), we calculate that

cosðsÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃ

cos

ðsÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 sin

ðsÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2



sin



arcsinðtÞ



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 t

We may now obtain the formula for the derivative of arcsin (t) by using the

Inverse Function Deri vative Rule that we learned in Section 3.6:

arcsinðtÞ5

sinðsÞj

s5arcsinðtÞ

cosðsÞj

s5arcsinðtÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 t

The derivative of arccos (t) is calculated in the same way. ’

From formula (3.10.1), we see that arcsin

(t) . 0. In Chapter 4, we will learn

that this inequality is the analytic characterization of a graphical property that we

have already observed: The inverse sine is an increasing function. Similarly, for-

mula (3.10.2) shows that arccos

(t) , 0 for all t A (21, 1). In Chapter 4, we will learn

that this inequality implies that the inverse cosine is a decreasing function, which

we have already observed from its graph.

⁄ EX

AMPLE 3 Calculate

arcsinðxÞ



x50

and

arccosðxÞ



x51=2

1

y  Cos(x)



m Figure 5

1

y  Cos(x)

y  x

␲

y  arccos(x)

m Figure 6

3.10 Other Transcendental Functions 255

Solution From (3.10.1) and (3.10.2), we obtain

arcsinðxÞ



x50

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

12x



x50

5 1

and

arccosðxÞj

x51=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

12x



x51=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ð1=2 Þ

ﬃﬃﬃ

: ¥

In Chain Rule form, the derivative formulas of Theorem 1 become

arcsinðuÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 u



ð3:10:3Þ

and

arccosðuÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 u



: ð3:10:4Þ

⁄ EX

AMPLE 4 Calculate the following derivatives:

arcsin







x522=

ﬃﬃ

and

arccosð

ﬃﬃﬃ



x51=4

Solution Using

(3.10.3) with u 5 1/x and du/dx 521/x

, we obtain

arcsin







x522=

ﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

12ð1=xÞ









x522=

ﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 3=4





4=3



1=2



Using (3.10.4) with u 5

ﬃﬃﬃ

and du=dx 5 ð1=2Þx

21=2

, we have

arccosð

ﬃﬃﬃ



x51=4

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

12ð

ﬃﬃﬃ





21=2





x51=4

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ð1=2 Þ





ﬃﬃﬃﬃﬃﬃﬃﬃ

1=4



ﬃﬃﬃ

: ¥

⁄ EX

AMPLE 5 Let a be

a positive constant. Show that

arcsin





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

: ð3:10:5Þ

Solution Setting u 5 x/a in

formula (3.10.3), we calculate

arcsin





arcsinðuÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 u



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ðx=aÞ



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

: ¥

256 Chapter 3 The Derivative

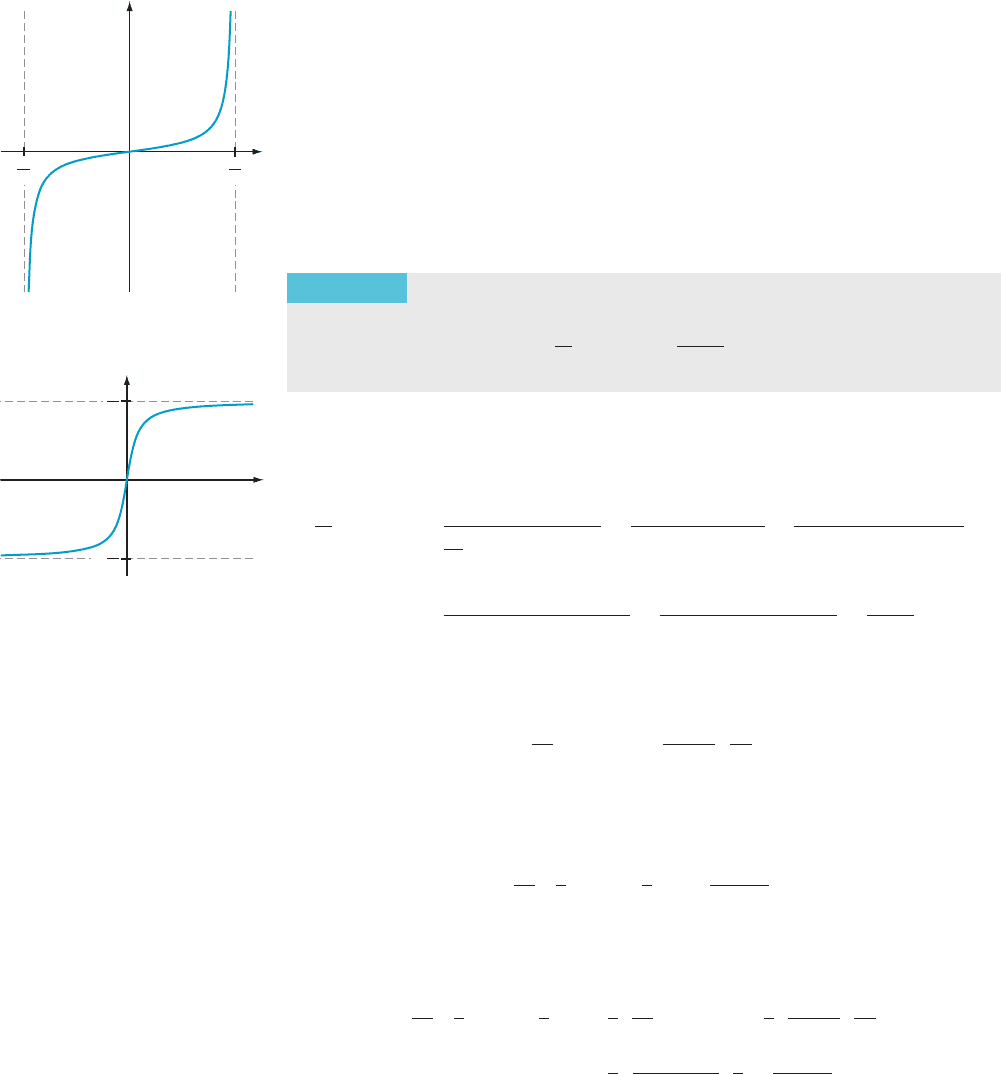
The Inverse Tangent

Function

Deﬁne the function x / Tan(x) to be the restriction of x / tan (x) to the interval

(2π/2, π/2). See Figure 7 for the graph of y 5 Tan(x). Because the function Tan is a

one-to-one, onto function with domain (2π/2, π/2) and range (2N,N), the inverse

function Tan

exists. We read Tan

(x) as “the inverse tangent of x” or “the

arctangent of x.” The notation arctan (x) is often used instead of Tan

(x).

The domain of Tan

(x)is(2N,N), and its image is (2π/2, π/2). The graph of the

arctangent is shown in Figure 8.

⁄ EX

AMPLE 6 Calculate arctan (1), arctanð

ﬃﬃﬃ

Þ, and arctanð2 1=

ﬃﬃﬃ

Þ:

Solution We

calculate arctan (t) by ﬁnding the unique s between 2π/2 and π/2 for

which tan (s) 5 t. Thus arctan ð1Þ5 π=4; arctanð

ﬃﬃﬃ

Þ5 π=3; and arctanð2 1=

ﬃﬃﬃ

Þ5

2 π=6.

THEOREM 2

The function t / arctan (t) is differentiable for every t and

arctanðt Þ5

1 1 t

: ð 3 :10:6Þ

Proof. As

usual, we calculate the derivative of a new inverse funct ion by using the

method of Section 3.6:

arctanðtÞ 5

TanðsÞ



s5arctanðtÞ

sec

ðsÞj

s5arctanðtÞ

1 1 tan

ðsÞj

s5arctanðtÞ

1 1 ðtanðsÞÞ



s5arctanðtÞ

1 1 ðtanðarctanðtÞÞÞ

1 1 t

’

The Chain Rule form of the inverse tangent derivative formula is

arctanðuÞ5

1 1 u



: ð3:10:7Þ

⁄ EX

AMPLE 7 Let a be a positive constant. Show that



arctan





1 x

: ð3:10:8Þ

Solution Using

equation (3.10.7) with u 5 x/a, we calculate



arctan







arctanðuÞ5



1 1 u



1 1 ðx=aÞ



1 x

: ¥

y  Tan(x)



␲

m Figure 7

y  Tan

1

(x)

␲



␲

m Figure 8

3.10 Other Transcendental Functions 257

Other Inverse

Trigonometric

Functions

We will say just a few words about the inverse cotangent, the inverse secant, and

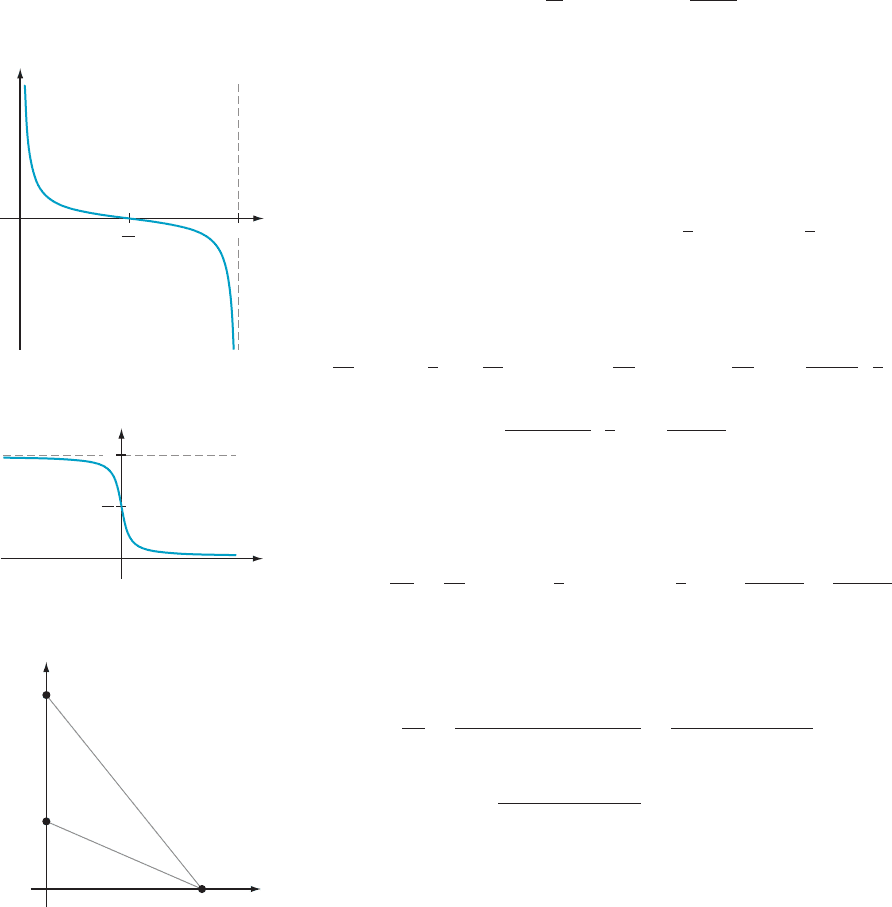
the inverse cosecant (because they do not arise frequently). We use x / Cot(x)to

denote the restriction of the cotangent function to the interval (0, π). From the

graph of y 5 Cot(x) in Figure 9, we see that x / Cot(x) is a decreasing function

that takes on all real values. Consequently, the inverse function Cot

:(2N,N) -

(0, π) exists. Refer to Figure 10 for its graph. We sometimes write Cot

(x)as

arccot (x). A computation similar to that of Theorem 2 yields the derivative of the

inverse cotangent:

arccotðtÞ52

1 1 t

: ð3:10:9Þ

⁄ EX

AMPLE 8 Figure 11 shows two ﬁxed points T 5(0, 8) and B 5 (0, 2) on

the y-axis and a variable point W 5 (x, 0) on the x-axis. The radian measure α of

+TWB is a function of x. Calculate dα/dx.

Solution From

Figure 11, we see that cot (α 1 ψ) 5 x/8, and cot (ψ) 5 x/2. It follows

that

α 5 ðα 1 ψÞ2 ψ 5 arccot





2 arccot





Both inverse cotangents in this equation have the form arccot (x/a). Letting u 5 x/a,

we use equation (3.10.9) and the Chain Rule to calculate

arccot





arccotðuÞ5

arccotðuÞ

1 1 u



1 1 ðx=aÞ



1 x

ð3:10:10Þ

We may replace a with 2 and 8 in (3.10.10). If we subtract the resulting formulas,

then we obtain

dα



arccot





2 arccot





1 x

We complete the calculation by expressing the right side of this last equation in

terms of a common denominator. We have

dα

2ð64 1 x

Þ2 8ð4 1 x

ð4 1 x

Þð64 1 x

96 2 6x

ð4 1 x

Þð64 1 x

526 

ðx

2 16Þ

ð4 1 x

Þð64 1 x

: ¥

ð3:10:11Þ

For

the inverse secant, we deﬁne x / Sec(x) to be the restriction of the secant to

the set [0, π/2) , (π/2, π]. From Figure 12, we see that x / Sec(x) is one-to-one

with image consisting of all numbers greater than or equal to 1 and all numbers less

than or equal to 21. The inverse function

y  Cot(x)

x 

␲

m Figure 9

y  Cot

1

(x)

␲

m Figure 10

(0, 8)

(0, 2)

(

x, 0

)





m Figure 11

258 Chapter

3 The Derivative

Sec

: ð2 N; 2 1,½1; NÞ-½0; π=2Þ,ðπ=2; π

is plotted in Figure 13. We sometimes write arcse c (x) for Sec

(x) and read

“arcsecant” instead of “inverse secant .” The derivative of the arcsecant is given by

arcsecðtÞ5

jtj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

; jtj. 1: ð3:10:12Þ

⁄ EX

AMPLE 9 Derive formula (3.10.12).

Solution The

derivation is quite similar to the ones we have already carried out,

but the absolute value in formula (3.10.12) alerts us to the need for paying careful

attention to the signs of the terms that arise. Applying the Inverse Function

Derivative Rule, we have

arcsecðtÞ5

SecðsÞ



s5arcsecðtÞ

secðsÞtanðsÞj

s5arcsecðtÞ

sec



arcsecðtÞ



tan



arcsecðtÞ



t  tan



arcsecðtÞ



ð3:10:13Þ

Next, trigonometric identity (1.6.2) with θ 5 arcsec (t) gives us tan

(arcsec (t)) 5

sec

(arcsec (t))21 5 t

2 1, or tanðarcsecðtÞÞ56

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

.Ift . 1, then 0 ,

arcsec(t) , π/2 and tan (arcsec (t)) . 0. Therefore tan



arcsecðtÞ



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

for

t . 1. In this case, t 5 jtj and (3.10.13) becomes

arcsecðtÞ5

t  tan



arcsecðtÞ



jtjð1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

jtj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

If t ,21, then π/2 , arcsec (t) , π and tan (arcsec (t)) , 0. Therefore

tanðarcsecðtÞÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

for t ,21. In this case, t 52|t| and (3.10.13) becomes

arcsecðtÞ5

t  tan



arcsecðtÞ



t ð2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

ð2 tÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

jtj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

: ¥

We obtain the ﬁnal inverse trigonometric function by deﬁning x / Csc(x)t

be the restriction of the cosecant to the set [2π/2, 0) , (0, π/2]. The graph is

exhibited in Figure 14. We see that x / Csc(x) is one-to-one and therefore has an

inverse function Csc

that maps the image of Csc to the domain of Csc. As x

ranges over the values in the domain of Csc, sin (x) takes on all values in the

interval [21, 1] except for 0. Therefore the cosecant takes on all values greater than

or equal to 1 and all values less than or equal to 21. Thus Csc

has domain (2N,

21] , [1,N) and range [2π/2, 0) , (0,π/2]. Its graph is shown in Figure 15. The

derivative of the inverse cosecant is given by

(0, 1)

(␲, 1)

y  Sec(x)

1

␲

m Figure 12

(1, ␲)

(1, 0)

11

 Sec

1

(x)

y  Sec

1

(x)

␲

m Figure 13



, 1



y  Csc(x)

␲

, 1

␲





m Figure 14

y  Csc

1

(x)

y  Csc

1

(x)

11

1,

␲





␲



m Figure 15

3.10 Other Transcendental Functions 259

Csc

ðxÞ52

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

; jxj. 1: ð3:10:14Þ

Notation In this section we have carefully distinguished between the trigonometric functions

and their restrictions to domains on which they are invertible. This has led us to

use the notations Sin

, Cos

, Tan

, and Sec

. It is standard practice among

mathematicians and scientists to simply write sin

, cos

, tan

, and sec

. When

you see an expression such as tan

(x), remember that it refers to the inverse of a

restriction of the tangent. It is especially important not to confuse an inverse tri-

gonometric function (such as Tan

(x)) with the reciprocal of the corresponding

trigonometric function (such as (Tan(x))

5 1/Tan(x)). The “arc” notation elim-

inates this danger.

The Hyperbolic

Functions

In eng ineering, physics, and other applications, certain special funct ions called the

hyperbolic functions arise frequently. Here we shall deﬁne and brieﬂy discuss them.

DEFINITION

The hyperbolic cosine of t is deﬁned to be

cosh ðtÞ5

1 e

for all real numbers t. The hyperbolic sine of t is deﬁned to be

sinh ðtÞ5

2 e

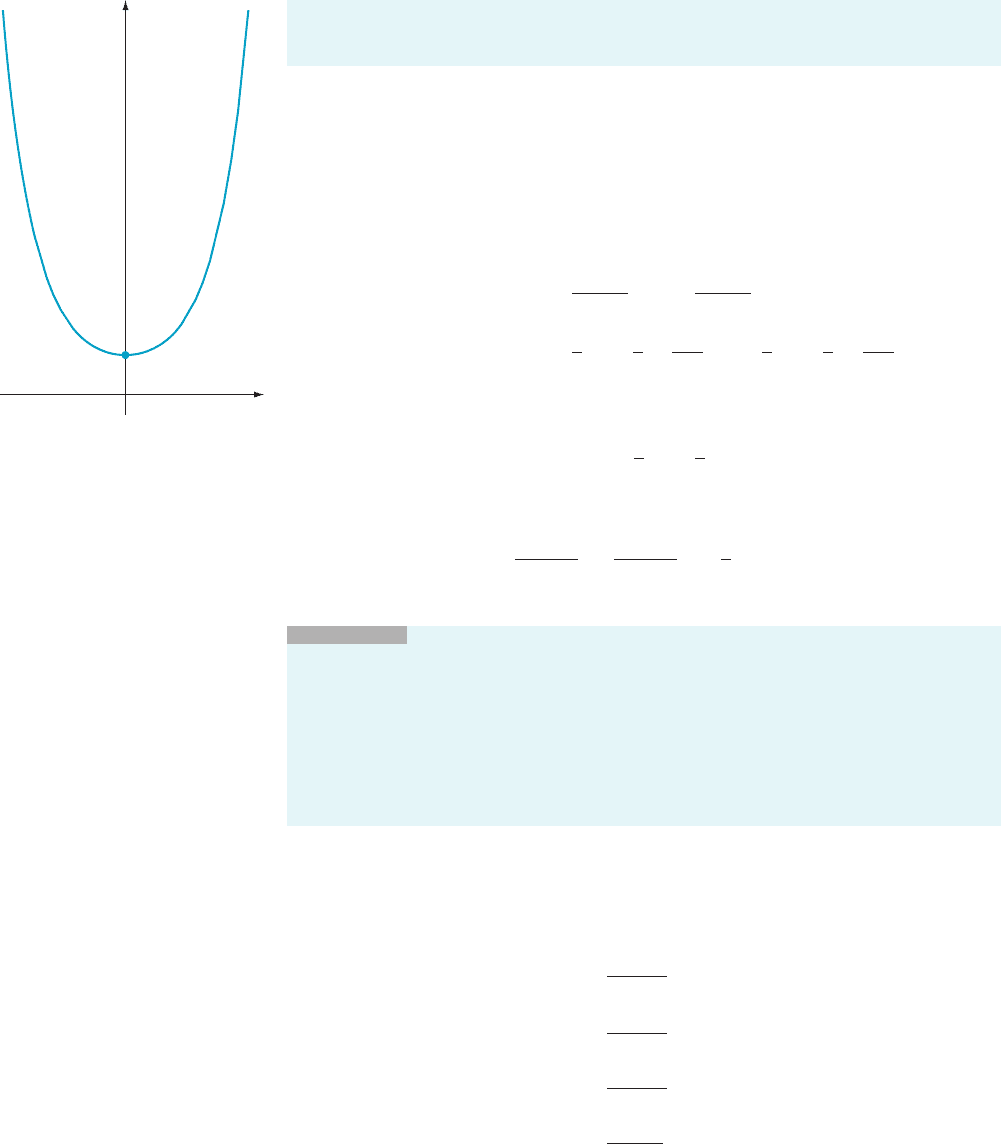
The graphs of the hyperbolic sine and cosine are given in Figures 16 and 17.

Notice that the hyperbolic cosine, like the ordinary cosine, is an even function.

That is, cosh (2t) 5 cosh (t). The hyperbolic sine, like the ordinary sine, is an

odd function: sinh (2t) 52sinh (t).

INSIGHT

Why is the term “hyperbolic” used? Recall that, for classical trigonometry

based on the unit circle, the numbers

x 5 cos ðtÞ and y 5 sin ðtÞ

satisfy x

5 1. That is, the point (cos (t), sin (t)) lies on the unit circle.

By contrast, the numbers

x 5 cosh ðtÞ and y 5 sinh ðtÞ

satisfy

2 y









1 2 1 e

22t

2 2 1 e

22t

5 1:

The hyperbolic cosine and hyperbolic sine therefore satisfy the identity

cosh

ðtÞ2 sinh

ðtÞ5 1: ð3:10:15Þ

m Figure 16 y 5 sinh(t)

260 Chapter 3 The Derivative

In other words, the point (cosh (t), sinh (t)) lies on the “unit hyperbola” whose

equation is x

5 1.

⁄ EXAMPLE 10 Show that

coshð2tÞ5 cosh

ðtÞ1 sinh

ðtÞ and sinhð2tÞ5 2sinhðtÞcoshðtÞ:

Solution The

basic method of establi shing identities among the hyperbolic

trigonometric functions is to convert them to exponential functions. Thus

cosh

ðtÞ1 sinh

ðtÞ5

















On simpliﬁcation, we obtain

cosh

ðtÞ1 sinh

ðtÞ5

22t

5 coshð2tÞ:

Similarly

2 sinh ðtÞcosh ðtÞ5 2



2 e



1 e



ðe

2 e

22t

Þ5 sinh ð2tÞ: ¥

INSIGHT

There are many analogies between the standard trigonometric functions

and the hyperbolic trigonometric functions. Compare the identities in Example 10 with

the circular trigonometric identities

cos ð2tÞ5 cos

ðtÞ2 sin

ðtÞ and sin ð2tÞ5 2 sinðtÞcosðtÞ:

As a rule of thumb, there is a hyperbolic trigonometric formula for every circular tri-

gonometric formula. But you must exercise some caution because there are some dif-

ferences in the occurrence of minus signs.

Just as the tangent, the cotangent, the secant, and the cosecant can be deﬁned as

quotients involving the sine and cosine, so can the hyperbolic tangent (tanh), hyper-

bolic cotangent (coth), hyperbolic secant (sech), and hyperbolic cosecant (csch):

tanhðtÞ 5

sinhðtÞ

coshðtÞ

; all real t;

cothðtÞ 5

coshðtÞ

sinhðtÞ

; t 6¼ 0;

sech ðtÞ 5

coshðtÞ

; all real t;

csch ðtÞ 5

sinhðtÞ

; t 6¼ 0:

(0, 1)

m Figure 17 y 5 cosh(t)

3.10 Other Transcendental Functions 261

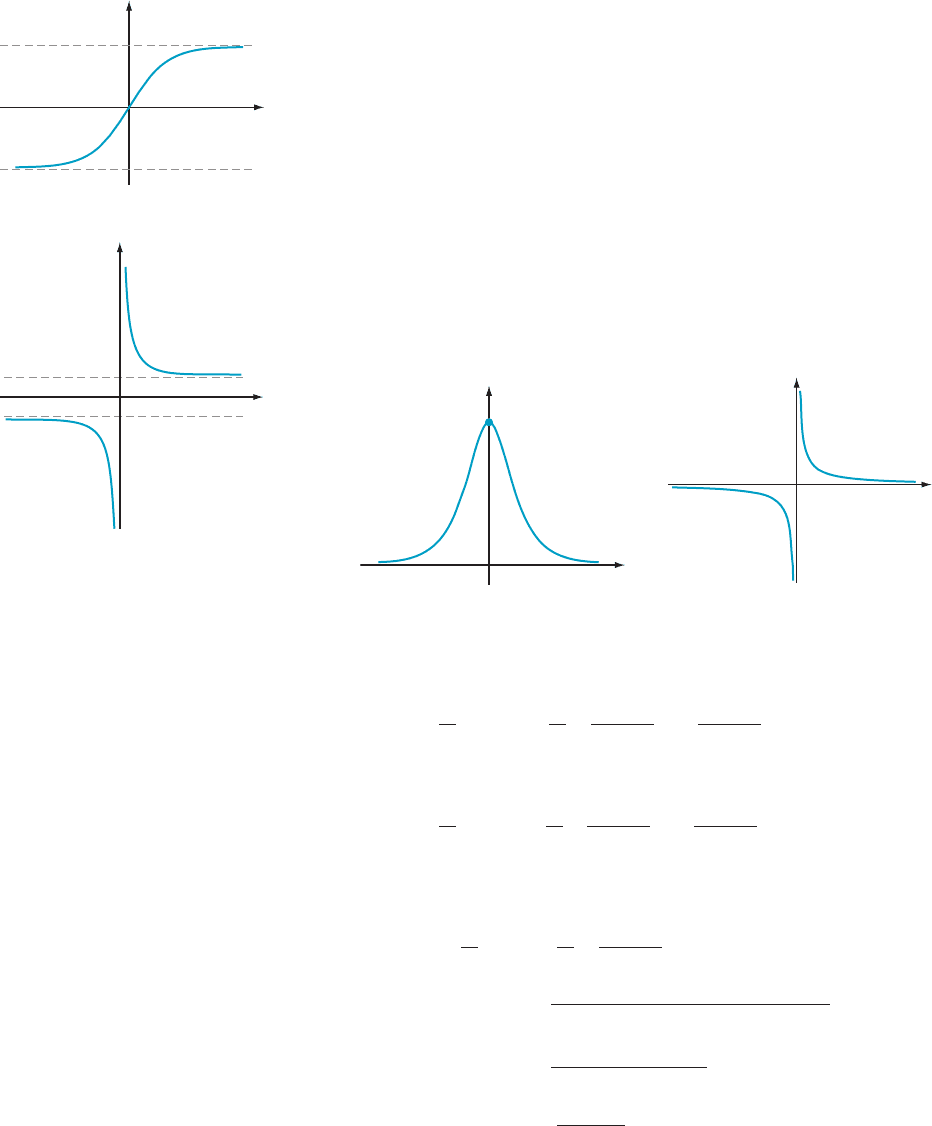
The graphs of these hyperbolic functions are given in Figures 18, 19, 20, and 21. Notice

that the graphs of y 5 tanh (x) and y 5 coth (x) have the lines y 5 1 and y 521as

horizontal asymptotes:

lim

x-N

tanhðxÞ5 lim

x-N

coth ðxÞ5 1 and lim

x- 2 N

tanhðxÞ5 lim

x- 2 N

cothðxÞ521:

The graphs of sech and csch have the line y 5 0 as a horizontal asymptote:

lim

x-N

sech ðxÞ5 lim

x- 2 N

sech ðxÞ5 0 and lim

x-N

csch ðxÞ5 lim

x- 2 N

csch ðxÞ5 0:

The graphs of coth and csch have the line x 5 0 as a vertical asymptote:

lim

x-0

cschðxÞ5 lim

x-0

cothðxÞ5 N an d lim

x-0

cschðxÞ5 lim

x-0

coth 52N:

Derivatives of the

Hyperbolic Functions

It is easy to calculate that

cosh ðtÞ5



1 e



2 e

5 sinh ðtÞ:

Similarly,

sinh ðtÞ5



2 e



1 e

5 cosh ðtÞ:

The calculation of the derivatives of the remaining four hyperbolic functions

follow from these formulas and the Quotient Rule. For example,

tanh 5



sinh ðtÞ

cosh ðtÞ



cosh ðtÞsinh

ðtÞ2 sinh ðtÞcosh

ðtÞ

cosh

ðtÞ

cosh

ðtÞ2 sinh

ðtÞ

cosh

ðtÞ

cosh

ðtÞ

5 sech

ðtÞ:

y  1

y  1

y  coth(x)

m Figure 19

y  tanh(x)

y  1

y  1

m Figure 18

(0, 1)

y  sech(x)

m Figure 20

y  csch(x)

m Figure 21

262 Chapter

3 The Derivative

The six differentiation formulas for the hyperbolic trigonometric functions are

listed in the following table.

sinh ðtÞ 5 coshðtÞ

cothðtÞ 52csch

ðtÞ

coshðtÞ 5 sinhðtÞ

sech ðtÞ 52sech ðtÞtanhðtÞ

tanhðt Þ 5 sech

ðtÞ

csch ðtÞ 52csch ðtÞcothðtÞ

The Inverse Hyperbolic

Functions

Because the hyperbolic sine is increasing on the entire real line, it is one-to-on e.

We may therefore discuss its inverse, sinh

(x) (or arcsinh(x)). The other hyper-

bolic functions are either not one-to one, or not onto R. But if their domains and

ranges are suitably restricted, then their inverses may be deﬁned. These inverses

may be calculated explicitly in terms of funct ions that we already understand.

⁄ EX

AMPLE 11 Show that

sinh

ðxÞ5 ln



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1



Solution Let y 5 sinh

(x). Then sinh (y) 5 x,ore

2 e

5 2x. If we let u 5 e

then our last equation becomes u 2 u

5 2x,oru

2 2x  u 2 1 5 0. We may solve

this quadratic equation in u by using the Quadratic Formula:

u 5

2x 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð2 2 x Þ

2 4ð1Þð2 1Þ

5 x 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

Because u 5 e

cannot be negative, the positive sign is used. Thus

5 u 5 x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

. From this we conclude that y 5 lnðx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

Þ: ¥

For reference, the following list provides the formulas for the inverses of the

hyperbolic functions.

sinh

ðxÞ 5 ln ðx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

Þ; all real x;

cosh

ðxÞ 5 ln ðx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

Þ; x $ 1;

tanh

ðxÞ 5



1 1 x

1 2 x



; 2 1 , x , 1;

coth

ðxÞ 5



x 1 1

x 2 1



; jxj. 1;

sech

ðxÞ 5 ln



1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x



; 0 , x # 1;

csch

ðxÞ 5 ln



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

jxj



; x 6¼ 0:

3.10 Other Transcendental Functions 263

The following list shows the basic derivative rules for the inverse hyperbolic

functions,

sinh

ðxÞ 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

all real x;

cosh

ðxÞ 52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

jxj. 1;

tanh

ðxÞ 5

1 2 x

2 1 , x , 1;

sech

ðxÞ 52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

0 , x , 1

The next example will derive these equations in a somewh at more general form.

⁄ EX

AMPLE 12 Let a be a positive constant. Show that

sinh





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

; ð3:10:16Þ



tanh





2 x

; ð3:10:17Þ

and



sech





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

: ð3:10:18Þ

Solution We

can use the explicit formulas for the inverse hyperbolic functions. For

example, because sinh

ðxÞ5 lnðx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

Þ; we have

sinh





5 ln



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1



5 ln



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



5 ln



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



5 ln



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



2 lnðaÞ:

Therefore for u 5 x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a

,wehave

sinh







lnðx 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a

Þ2 lnðaÞ



lnðuÞ2

lnðaÞ5

lnðuÞ:

We apply the Chain Rule to obtain

sinh





lnðuÞ



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a





x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a





1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



The rest of the calculation consists of algebraic simpliﬁcation:

sinh

ðxÞ5

x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a





1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a





x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 a

264 Chapter 3 The Derivative