Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Similarly, from

tanh





5 tanh

ðvÞj

v5x=a



11v

12v





v5x=a



1 1 x=a

1 2 x=a





a 1 x

a 2 x



lnða 1 xÞ2

lnða 2 xÞ;

we obtain

tanh

ðxÞ5



ln ða 1 xÞ2

lnða 2 xÞ





a 1 x

a 2 x



2 x

and (3.10.17) follows. These derivatives can also be calculated using the Inverse

Function Derivative Rule. Let us use that rule for the remaining calculation. We

will need the identity

1 2 tanh

ðtÞ5 sech

ðtÞ; ð3:10:19Þ

which is obtained by dividing each term of identity (3.10.15) by cosh

(t). Let x be

positive (so that it is in the domain of the hyperbolic secant), and set y 5 sech

(x).

Notice that y is positive and therefore tanh (y) is also positive. From this obser-

vation and identity (3.10.19), it follows that tanh (y) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 sech

ðyÞ

: Because

y 5 sech

(x), we have x 5 sech(y)and

sech

ðxÞ5

sechðyÞ

sech ðyÞtanh ðyÞ

sech ðyÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 sech

ðyÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

Finally, applying the Chain Rule form of this derivative rule with u 5 x/a,wehave

sech





sech

ðuÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 u



ðx=aÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ðx=a Þ



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

and formula (3.10.18) results.

A LOOK FORWARD c It is certainly possible to do without the hyperbolic

trigonometric functions because they are merely arithmetic combinations of

functions that we already know and understand. However, knowledge of these

new functions enables us to recognize certain patterns and expressions that arise

frequently in applications. They also simplify many formulas, as we wi ll see in

Chapters 4 and 6.

3.10 Other Transcendental Functions 265

Summary of Derivatives of Basic Functions

ðx

Þ 5 px

p21

2 N , p , N

sin ðx Þ 5 cos ðxÞ

cos ðxÞ 52sin ðxÞ

tan ðxÞ 5 sec

ðxÞ

cot ðx Þ 52csc

ðxÞ

sec ðx Þ 5 sec ðxÞtan ðxÞ

csc ðxÞ 52csc ðxÞcot ðxÞ

5 e

5 a

 ln ðaÞ

lnðxÞ 5

log

ðxÞ 5

x  lnðaÞ

arcsinðxÞ 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

arccosðxÞ 52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

arctanðxÞ 5

1 1 x

arcsecðxÞ 5

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

QUICK QUIZ

1. True or false: sin (arcsin (t)) 5 t for every t in [21, 1].

2. True or false: arccos (cos (s)) 5 s for every real number s.

3. True or false: Tan

(x) 5 cot (x).

4. Simplify: cosh (ln (x )).

Answers

1. True 2. False 3. False 4. (x

11) / (2x)

266 Chapter 3 The Derivative

EXERCISES

Problems for Practice

c In Exercises 118, calculate the value of the given inverse

trigonometric function at the given point. b

1. arcsin

(1)

2. arcsin (

ﬃﬃﬃ

/2)

3. arcsin (21)

4. arccos (21)

5. arccos (1/2)

6. arccos (2

ﬃﬃﬃ

/2)

7. arccos (

ﬃﬃﬃ

/2)

8. arctan (21)

9. arctan (2

ﬃﬃﬃ

)

10. arcsec (2)

11. arcsec (

ﬃﬃﬃ

)

12. arccsc (1)

13. arccsc (2

ﬃﬃﬃ

)

14. arccot (2

ﬃﬃﬃ

)

15. arcsin ðsin ð5π=4ÞÞ

16. arctan ðtan ð2 3π=4ÞÞ

17. arcsec ðsecð2 5π=6ÞÞ

18. arccos (cos (4π/3))

c In Exercises 1934, differentiate the given expression with

respect

to x. b

19. arcsin

(1 2 x)

20. arcsin (

ﬃﬃﬃ

)

21. x arcsin (x)

22. arccos (x

)

23. log

(arccos (x

))

24. cos (arctan (x))

25. arctan (e

)

26. arctan (2/x)

27. x arctan (x)

28. arctan (x)/x

29. x

arcsec (x)

30. arcsec (1/x)

31. arccsc (x

)

32. arccsc (sin (x))

33. arccot (

ﬃﬃﬃ

)

34. arccot (1/x

)

c In Exercises 3554, differentiate the given expression with

respect

to x. b

35. sinh

(3x)

36. sinh (ln (x))

37. ln (sinh (x))

38. cosh (x 2 2)

39. cosh (x)/x

40. cosh

(x)

41. ln (tanh (x))

42. tanh (ln (x 1 2))

43. tanh (tan (x))

44. x sech (x)

45. sech

ﬃﬃﬃ

46. coth (x

)

47. sinh

(5x)

48. x sech

(3x)

49. arctan (sinh (x))

50. arcsin (tanh (x))

51. tanh

(cos (x))

52. tanh

(coth (x))

53. tanh

(cosh (x))

54. sinh

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

Further Theory and Practice

c In Exercises 5558, ﬁnd the linearization of the given

function f (x) at the given point c. b

55. f (x) 5 arcsin

(x), c 5 1/2

56. f (x) 5 arcsin (x), c 521/

ﬃﬃﬃ

57. f (x) 5 arctan (x), c 5

ﬃﬃﬃ

58. f (x) 5 arctan (x), c 521

59. Show that arcsin (x) 5 π/22arccos (x) for all x in [21, 1].

60. Show that arctan (x) 5 arccot (1/x) for all x . 0 and

arctan (x) 5 arccot (1/x)2π for all x , 0.

61. Show that cos

(arcsin (x)) is the restriction to the interval

[21, 1] of a polynomial in x.

62. Show that cos (2 arccos (x)) is the restriction to the

interval [21, 1] of a polynomial in x.

63. Verify the identity cosh (x 1 y) 5 cosh (x) cosh (y) 1

sinh (x) sinh (y).

64. Verify the identity sinh (x 1 y) 5 sinh (x) cosh (y) 1

cosh (x) sinh (y).

65. Verify the identity cosh(2x) 5 2 cosh

(x) 2 1.

66. Verify the identity cosh(2x) 5 2 sinh

(x) 1 1.

67. Verify the identity

tanh ðx 1 yÞ5

tanh ðxÞ1 tanh ðyÞ

1 1 tanh ðxÞtanh ðyÞ

68. Show that



cosh ðxÞ1sinh ðxÞ



5 cosh ðnxÞ1 sinh ðnxÞ

for any n, integer or not.

69. Show that y 5 sinh (ωx) and y 5 cosh (ωx) are solutions of

the differential equation y

ðxÞ2 ω

yðxÞ5 0:

Let a be a positive constant, and set

TðxÞ5 a  sech





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

c Exercises 70 and 71 are

concerned with the graph of

y 5 T(x). Such a curve is called a tractrix. b

70. Show

that T

ðxÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

71. The tip of a boat is at the point (a,0)onthex-axis. A tether

of length a is attached to the tip of the boat and extends to

3.10 Other Transcendental Functions 267

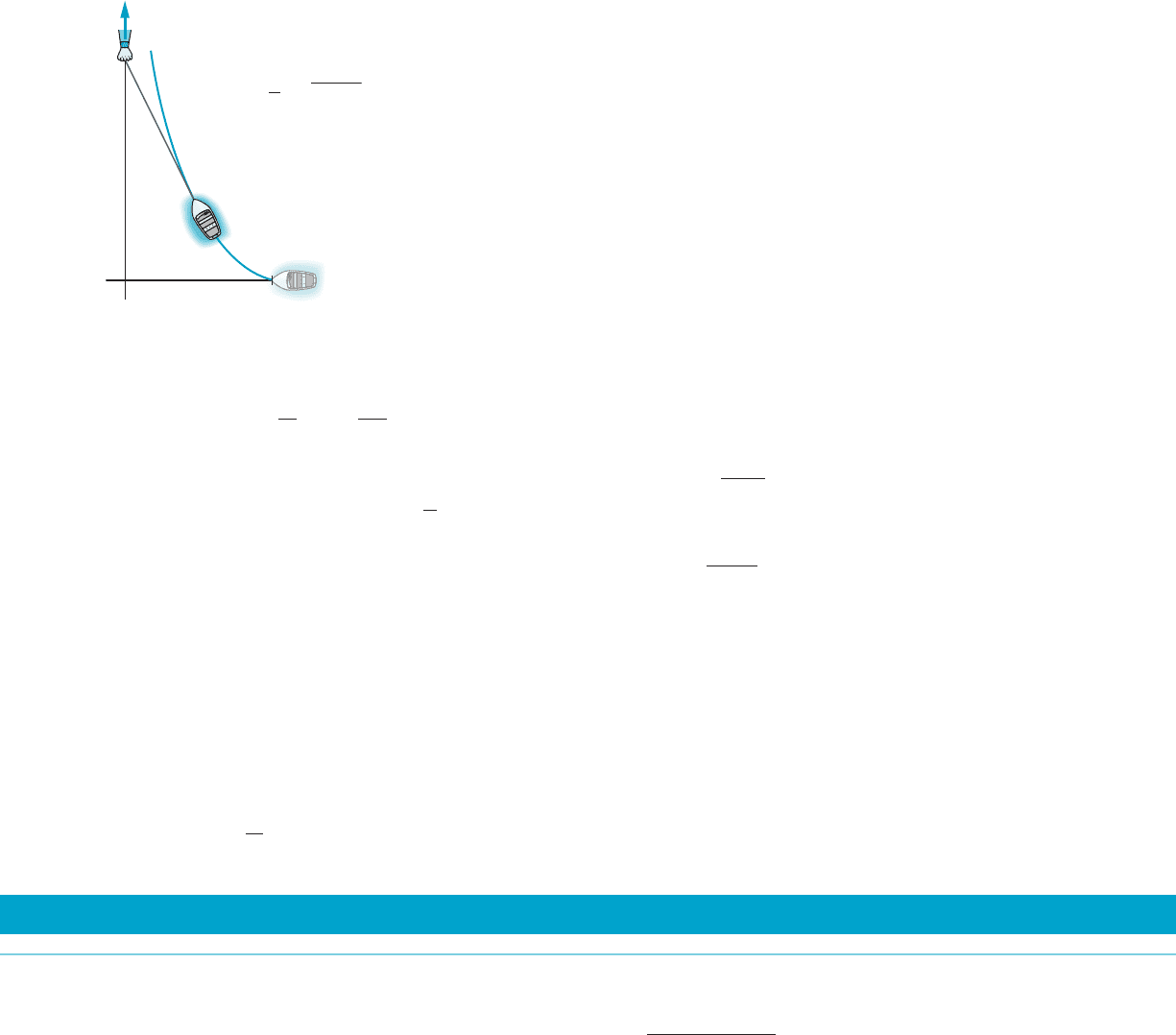
the origin. The boat is pulled by the tether as in Figure 22.

Show that the tip of the boat moves along a tractrix.

Tractrix

Tether

T(x)  a sech

1



 x







m Figure 22

72. The

velocity of a water wave of wavelength λ as a func-

tion of the depth d of the water is given by

v 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2π

λtanh



2πd



Use the linear approximation of tanh (x)atx 5 0 to show that

vðdÞ

ﬃﬃﬃﬃﬃﬃ

for small d. By considering the horizontal asymp-

tote of the hyperbolic tangent, show that v 

ﬃﬃﬃﬃﬃﬃﬃﬃ

2π

for large d.

The gudermanian function gd deﬁned by

gdðuÞ5 arctanðsinhðuÞÞ

links the usual trigonometric functions and the hyperbolic

functions. Exercises 7375 concern

the gudermanian.

73. Show

that

coshðuÞ5 secðgdðuÞÞ

tanhð uÞ5 sinð gdðuÞÞ

cothðuÞ5 cscðgdðuÞÞ

sechðu Þ5 cosð gdðuÞÞ

cschðuÞ5 cotðgdðuÞÞ:

74. Show that gd

ðuÞ5 sechðuÞ.

75. Use the Inverse Function Derivative Rule to show that

dθ

ðθÞ5 secðθÞ:

c A real-valued function f of

a real variable x is said to be

algebraic if there is a polynomial p(u, v) with integer coefﬁ-

cients such that p(x, f (x)) 5 0 for all x. For example, f (x) 5

2x1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

is algebraic because

pðx; f ðxÞÞ5 3x



2x1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ



2 4x



2x 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1



2 1

 0

for p(u, v) 5 3u

2 4uv 2 1. A function that is not alge-

braic is said to be transcendental. In Exercises 7679,

ﬁnd a

polynomial that shows that the given expression is

algebraic. b

76. x2

ﬃﬃ

ﬃ

77.

ﬃﬃﬃ

78. 2 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x=x

79.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1

ﬃﬃﬃ

Calculator/Computer Exercises

c In Exercises 8085, use a central difference quotient to

approximate f

ðcÞ for the given f and c. Plot the function and

the tangent line at (c, f (c)). b

80. f (x) 5 arcsin



1 1



, c 5 1.3

81. f (x) 5 x arcsec (11x

), c 5 2.1

82. f (x) 5 arcsin (2 arctan (x)/π), c 5 1.7

83. f ðxÞ5 sinh



1 1

ﬃﬃﬃ



, c 5 4.5

84. f (x) 5 arccos (tanh(x)), c 5 0.7

85. f (x) 5 sinh

(log

(x)), c 5 2.5

86. Graph the six hyperbolic functions in the rectangle

[0, 1.5] 3 [0, 2]. Identify the seven points of intersection in

the ﬁrst quadrant.

87. The Gudermannian function gd is deﬁned on the real line

by gd(u) 5 arctan (sinh (u)). Its inverse gd

is deﬁned on

(2π/2, π/2).

a. Graph gd.

b. Graph gd

by means of the parametric equations

x 5 gd(t) and y 5 t.

Summary of Key Topics in Chapter 3

Instantaneous Velocity

(Section 3.1)

If the position of a moving body at time t is

given by a function p(t), then the

quantity

lim

Δt-0

pðt 1 ΔtÞ2 pðtÞ

Δt

;

if it exists, is called the instantaneous velocity of the moving body.

268 Chapter 3 The Derivative

Tangent and

Normal Lines

(Section 3.1)

If f is

a function whose domain contains (a , b) and if c 2(a, b), then the slope of the

tangent line to the graph of f at c is equal to f

ðcÞ, provided that the derivative

exists. Thus the tangent line has equation

y 5 f

ðcÞðx 2 cÞ1 f ðcÞ:

The normal line to the curve at the point c is the line through (c, f (c)), which is

perpendicular to the tangent line at that point.

Yet another interpretation of the derivative involves rates of change. If f is a

function of a parameter x , then f

ðcÞ represents the instantaneous rate of change of

f with respect to x at the point c, provided that the derivative exists.

The Derivative

(Section 3.2)

In general, if f is

a function whose domain contains (a, b), if c 2(a, b), and if

lim

Δx-0

f ðc 1 ΔxÞ2 f ðcÞ

Δx

exists, then this quantity is called the derivative of f at the point c. It is denoted by

any of the notations

ðcÞ or Dðf ÞðcÞ or



f ðcÞ:

The process of calculating the derivative is called differentiation. A function that

possesses the derivative is called differentiable.

Derivatives of Special

Functions

(Sections 3.2, 3.4, 3.5, 3.6)

By direct calculation, we can determine the derivatives of a number of particular

functions.

These are:

5 p  x

p21

for any real number p:

Also

sinðxÞ5 cosðxÞ

cosðxÞ52sinðxÞ

tanðxÞ5 sec

ðxÞ

cotðxÞ52csc

ðxÞ

secðxÞ5 secðxÞtanðxÞ

cscðxÞ52cscðxÞcotðxÞ

5 e

5 a

 lnðaÞ

Summary of Key Topics 269

lnðxÞ5

log

ðxÞ5

x  lnðaÞ:

Rules for Taking

Derivatives

(Section 3.3)

We have

ðf 1 g Þ

5 f

1 g

ðf 2 g Þ

5 f

2 g

ðα  f Þ

5 α ðf

Þ; α constant

ðf  gÞ

5 f

 g 1 f  g





g  f

2 f  g

The Chain Rule

(Section 3.5)

If g(u)

and f (x) are differentiable functions, if the range of f is in the domain of g,

and if c is in the domain of f, then g 3 f is differentiable at c and

ðg 3 f Þ

ðxÞ5 g

ðf ðxÞÞ  f

ðxÞ:

In Leibniz notation, the Chain Rule is

dðg 3 f Þ



x5c



u5f ðcÞ





x5c

If we use variables u 5 f (x) and y 5 g(u) , then we may write the Chain Rule as



The Chain RulePower Rule is the case of the Chain Rule in which g(u) 5 u

5 pu

p21



The Inverse of a

Function and Its

Derivative

(Section 3.6)

If S, T are

open interval s, if f : S-T is invertible and differentiable, and if f

never

vanishes on S, then f

is differentiable on T. The derivative is given by the

formula

ðtÞ5

s5f

ðtÞ

provided that the denominator on the right is nonzero. Using prime notation, if

f (c) 5 γ and f

ðcÞ6¼0, then

ðf

ðγÞ5

ðcÞ

The exponential function exp (x) 5 e

has an inverse function with domain

(0, N). It is called the natural logarithm and is denoted by ln. (Its derivative has

been recorded earlier.)

270 Chapter 3 The Derivative

Higher Derivatives

(Section 3.7)

The derivative of a given function f (x)

is a new function f

ðcÞ. This new function

can in turn be differentiated, provided the derivative exists. The resulting function

is called the second derivative. It is denoted by

ðxÞ or f

ð2Þ

ðxÞ or

€

f ðxÞ or D

f ðxÞ:

The second derivative function can in turn be differentiated, and so on. The

derivative of the (k 2 1)

derivative function is called the k

derivative function. It

is denoted by the symbols

000

ðk primesÞ or f

ðkÞ

or D

f :

Leibniz’s rule for the second derivative of a product asserts that

ðf  gÞ

ð2Þ

5 f

ð2Þ

ð0Þ

1 2f

ð1Þ

1 f

ð0Þ

ð2Þ

Implicit Differentiation

(Section 3.8)

If F(x, y) 5 C is

an equation which expresses y implicitly as a function of x, then we

can differentiate it without ﬁrst solving for y as a function of x. This is the method

of implicit differentiation.

If x and y are expressed in terms of a parameter t by the equations x 5 ϕ

ðtÞ and

y 5 ϕ

ðtÞ, and if y is a different iable function of x, then

ðtÞ

dy=dt

dx=dt

Differential

Approximation

(Section 3.9)

If f is

differentiable at c, then f may be approximated at a nearby point c 1 Δx by

f ðc 1 Δ x Þf ðcÞ1 f

ðcÞΔx;

f ðxÞf ðcÞ1 f

ðcÞðx 2 cÞ:

Writing Δf (x) for f (x1h) 2 f (x), we have

Δf ðxÞf

ðxÞΔx

which is written in terms of differentials as

df ðxÞ5 f

ðxÞdx:

Inverse Trigonometric

Functions

(Section 3.10)

We obtain an inverse of each trigonometric function by restricting its domain. The

name

of the inverse function is obtained by preﬁxing “arc” to the name of the

trigonometric function. The derivative formulas are

arcsinðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

arccosðxÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

arctanðxÞ5

1 1 x

Summary of Key Topics 271

arccotðxÞ52

1 1 x

arcsecðxÞ5

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

arccscðxÞ52

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

Hyperbolic

Trigonometric

Functions

(3.10)

The basic hyperbolic trigonometric functions are deﬁned by

coshðxÞ5

1 e

and sinhðxÞ5

2 e

The four other hyperbolic trigonometric functions are deﬁned as ratios that are

analogous to those of standard trigonometry: tanh(x) 5 sinh ( x )/cosh (x), coth (x) 5

cosh (x)/sinh (x), sech ( x ) 5 1/cosh (x), and csch (x) 5 1/sinh (x). The derivative for-

mulas are

sinhðxÞ5 coshðxÞ

cothðxÞ52csch

ðxÞ

coshðxÞ5 sinh ðxÞ

sechðxÞ52sechðxÞtanhðxÞ

tanhðxÞ5 sech

ðxÞ

cschðxÞ52cschðxÞcothðxÞ:

If the domains and ranges of the hyperbolic trigonometric functions are sui-

tably restricted, then their inverses may be deﬁned. The basic derivative rules for

these inverse hyperbolic functions are

sinh

ðxÞ 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

all real x

cosh

ðxÞ 52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1

jxj. 1

tanh

ðxÞ 5

1 2 x

21 , x , 1

sech

ðxÞ 52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

0 , x , 1:

Review Exercises for Chapter 3

c In Exercises 112, calculate the slope-intercept form of

the tangent line to the graph of f at (c, f (c)) b

1. f (x) 5 x

, c 522

2. f (x) 5 3 x

24/3

, c 5 27

3. f (x) 5 12/

ﬃﬃﬃ

, c 5 16

4. f (x) 5 cos (2x),c 5 π/3

5. f (x) 5 12x sin (πx), c 5 1/6

6. f (x) 5 e

, c 5 ln (2)

7. f (x) 5 (2x

2 3)/x, c 5 3

8. f (x) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

, c 5 2

9. f (x) 5 2ln(x)/e 2 1/x, c 5 e

10. f (x) 5 e

/x, c 5 1/3

11. f (x) 5 3/2

, c 5 0

12. f (x) 5 5(1 1 x

)/(3 1 x), c 5 2

272 Chapter 3 The Derivative

c In Exercises 1362, differentiate the given expression with

respect to x. b

13.

ﬃﬃ

ﬃ

14. 1/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2x 1 1

15. (3 1 x)/x

16.

ﬃﬃﬃ

(3x

3/2

1 5x

5/2

)

17. x

1 1/x

18. 1/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 2 x

19. (x 2 1)(x 1 2)/x

20. x/(1 1 x

)

21. (2 1 x

)

22. (1 1 x

)/(2 1 x

)

23. sin (π 2 x)

24. cos (3x)

25. cos (2x 1 π/4)

26. tan (πx)

27. sec (2x)

28. csc (πx/2)

29. cot (1/x)

30. sin

(x)

31. sin

(5x

)

32. x

cos (2x)

33. x

sin (x

)

34. sin (x)/x

35. (1 1 sin (x))/(1 1 cos ( x))

36. tan (x)/(1 1 tan (x))

37.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 cosð3x

38. exp(22x)

39. xe

40. x

41. xe

/(1 1 x)

42. exp(x 1 ln(x))

43. 2

44. 10

2 10

45. 1/x 1 ln(x)

46. ln (3x 1 2)

47. x

ln (x)

48. ln (3/x) 1 3/ln (x)

49. ln (2 ln (3x))

50. log

(1 1 3

)

51. x

log

(x 1 2)

52. (2 1 x)

53. 2

3

5

54. arcsin (x/2)

55. arctan (2/x)

56. arcsec (x

)

57. arcsin (cos (x))

58. cosh(2x) 2 sinh(3x)

59. cosh(x

)

60. tanh(ln(x))

61. sinh

)

62. tanh

(1/x)

c In Exercises 6368, a particle’s position along the x-axis

given at time t. Calculate the particle’s velocity and

acceleration. b

63. 55 1 60t 2 16t

64. 18 sin (3t 1 π/2)

65. 20/(1 1 t

)

66. exp(2t)/(1 1 exp(2t))

67. 25 2 e

25t

68. ln (1 1 t

/4)

c In Exercises 6974, ﬁnd the point c such

that γ 5 f (c), and

use it to calculate ðf

ðγÞ. b

69. f (x) 5 x

1 3x 2 9, γ 5 5

70. f (x) 5 4/(11e

), γ 5 2

71. f (x) 5 x

/(41x

), γ 5 1

72. f (x) 5 x

ln (x),γ 5 0

73. f (x) 5 xe

, γ 5 e

74. f ðxÞ5 2

102x

; γ 5 4

c In Exercises 7580, use the method of implicit differ-

entiation

to ﬁnd dy/dx. b

75. exp(y) 2 x 1 y 5 1

76. y ln

(y) 5 1 1 x

77. x

2 y 1 y

5 16

78. x

1 xy 1 y

5 12

79. y 1 1/y 5 1 1 ln(x)

80. 1/x 1 1/y 5 4/(1 1 y)

c In Exercises 8184, use the method of implicit differ-

entiation

to ﬁnd dy/dx and d

y/dx

. b

81. y

1 y 2 x 5 15

82. y

1 xy 2 2x 5 6

83. sin (y) 1 2 cos (x) 5 1

84. e

2 xy 5 1

c In Exercises 8590, ﬁnd the slope-intercept form of the

tangent

line to the given parametric curve at the given value t

of the parameter. b

85. x 5 t

2 t, y 5 t

2 6, t

5 2

86. x 5 t

1 2, y 5 t

2 t, t

521

87. x 5 t 2 sin (t), y 5 1 2 cos (t), t

5 π/3

88. x 5 1 1 te

, y 5 2t 1 e

, t

5 0

89. x 5 t 1 ln (t), y 5 t 1 2/t, t

5 1

90. x 5 2t/(1 1 t

), y 5 (1 1 t)/(1 1 t

), t

5 1

c In Exercises 9194, use the differential approximation

with

base point c to estimate f (c 1 Δx). b

91. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

1 1 7x

, c 5 5, Δx 520.3

92. f (x) 5 (5 1 x

)

1/5

, c 5 3, Δx 5 0.3

93. f ðxÞ5 8x=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

9 2 x

, c 5 5, Δx 5 0.2

94. f (x) 5 (15 1 4x)

1/3

/x, c 5 3, Δx 520.4

Review Exercises 273

c In each of Exercises 9598, a function f, a point c, and

an increment h are given. Calculate f (c 2 h/2), f (c), and

f (c 1 h/2), and use these values to approximate f

ðcÞ. Then

calculate f (c 2 h) and f (c 1 h). Use these values to estimate

ðcÞ. b

95. f (x) 5 x

, c 5 1.418, h 5 0.002

96. f (x) 5 sin

(x), c 5 0.5236, h 5 0.0004

97. f (x) 5



xexp(x) 1 1





ln(x) 1

ﬃﬃﬃ



, c 5 3.14, h 5 0.0002

98. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 4

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1 5x

, c 5 3.0, h 5 0.002

274 Chapter 3 The Derivative