Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

GENESIS

DEVELOPMENT3

The Tangent Problem in Antiquity

Apollonius (ca. 260 B.C., Perga - ?) was the greatest

geometer of antiquity. His most important work was

Conics, written in eight books. The ﬁrst four of these

books have been preserved in Greek, the next three in

ninth-century Arabic translations. Book VIII has been

lost. Before Apollonius, the geometers of ancient

Greece did not ﬁnd an acceptable deﬁnition of the

tangent line to a curve. Apollonius, however, found a

sophisticated way to approach the difﬁculty. His insight

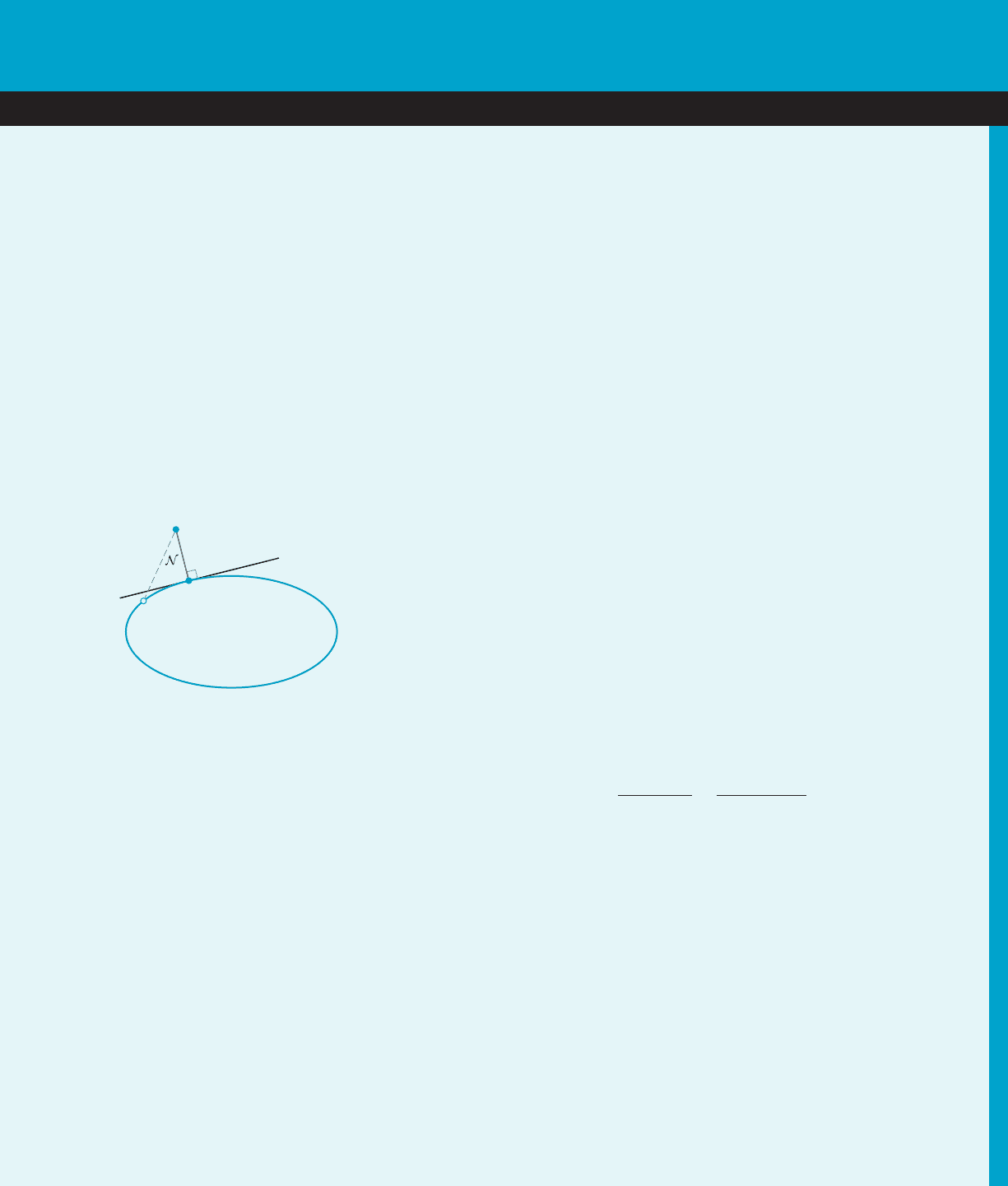
was to start with the normal line N. Given a curve C and

a point Q not on C, Apollonius constructed N by solving

a minimization problem: He found the point P on C

with minimum distance to Q (as in Figure 1). After

Apollonius obtained the normal line N 5 PQ, he took

the tangent to be the line through P perpendicular to N.

The Solutions of Fermat and Descartes to the

Tangent Problem

The introduction of analytic geometry revived the tan-

gent problem in the 1630s. Descartes described the pro-

blem as “ . . . the most useful and general that I have ever

wanted to know in geometry.” To ﬁnd the tangent at a

point P of a curve C, Descarteswould ﬁnd a circle that just

touched C at P without crossing C.LetO be the center of

this circle. Descartes took the line through P perpendi-

cular to OP to be the tangent of C. In effect, Descartes

had “reduced” the problemof ﬁnding a tangent line to the

seemingly more difﬁcult problem of ﬁnding a tangent

circle. This method appeared in La G

eom

etrie (1637),

accompanied by illustrative examples that did not reveal

how cumbersome a method it really was.

We will illustrate the method of Desc artes by

ﬁnding the tangen t line to y 5

ﬃﬃﬃ

at the point P 5

(c,

ﬃﬃﬃ

). We seek the circle with center (a, 0) and radius r

that just touches the given parabola at P. After writing

a as c 1 h, the equation of the circle becomes



x2ðc1hÞ



1 y

5 r

The parameters h and r are to be determined in terms

of the given value c. At the point P of intersection of

the circle and the parabola y 5

ﬃﬃﬃ

, the ordinate satis-

ﬁes y

5 x. Therefore the abscissa c of P satisﬁes the

second degree equation

QðxÞ5 ðx 2ðc1hÞÞ

1 x 2 r

5 0:

This means that x 2 c is a factor of Q(x). Descartes

reasoned that because the circle touches but does not

cross the parabola, the root c must have even multi-

plicity m. Because the degree of Q is 2, the only pos-

sibility is that m 5 2 and Q(x) 5 (x 2 c)

. Thus

(x 2 c)

5 x

1 (1 2 2(c 1 h))x 1 (c 1 h)

2 r

. Expand-

ing the left side, we obtain

2 2cx 1 c

5 x



1 2 2ðc 1 hÞ



x 1



ðc1hÞ

2 r



Each power of x must appear with the same coef-

ﬁcient on both sides of this identity. This leads to the

simultaneous equations: 22c 5 122(c 1 h) and

5 (c1h)

2 r

. Solving these equations, we obtain

h 5 1/2. The line N determined by the two points P 5

(c,

ﬃﬃﬃ

) and (c 1 h, 0), therefore, has slope

ﬃﬃﬃ

2 0

c 2 ðc 1 hÞ

ﬃﬃﬃ

2 0

c 2 ðc 1 1=2Þ

522

ﬃﬃﬃ

The slope of the line perpendicular to N, that is, the

slope of the tangent line, is therefore the negative

reciprocal of this number, or 1/(2

ﬃﬃﬃ

). See Figure 2. Of

course, nowadays we have a much easier time of it: The

Power Rule tells us that if f( x ) 5

ﬃﬃﬃ

5 x

1/2

, then

ðcÞ5 (1/2) c

21/2

5 1/(2

ﬃﬃﬃ

The method of Descartes becomes entirely

unwieldy when tried on even slightly more complicated

examples. One contemporary protested that the

method gives rise to computations that are a “ . . .

labyrinth from which it is extraordinarily difﬁcult to

emerge.” When Fermat learned of the work of Des-

cartes on tangents in 1637, he published his own

P

Tangent line

Normal line

m Figure 1

275

method for ﬁnding the tangent line to the graph of a

function f at c, a method that he had discovered some

time earlier. Fermat did not use the slope m of the

tangent line as a parameter. Instead, he used the length

s of the sub tangent. See Figure 3. Because m and s are

related by the equation m 5 f ( c)/s, the difference is

not signiﬁcant. Using the notation of Figure 3, we have

s/h 5 f (c)/(H 2 f (c)) by similar triangles. This allows us

to solve

m 5

f ðcÞ

H 2 f ðcÞ

Fermat argued that, when h is very small, H f (c 1 h).

He called this approximation an adequation. Fermat

made the substitution Hf (c1h), obtaining

m 

f ðc 1 hÞ2 f ðcÞ

For f a polynomial, Fermat expanded f (c1h) to obtain

a polynomial in h with constant term f (c):

f ðc 1 hÞ5 f ðcÞ1 f

ðcÞh 1 f

ðcÞh

1 ::: :

Thus

m 

ðcÞh 1 f

ðcÞh

1 :::

He then eliminated h from the denominator by can-

cellation

m  f

ðcÞ1 f

ðcÞh 1 :::

At this stage, Fermat either set h 5 0 or simply

discarded the terms with h as a factor—it is not clear

from his writing. In any event, Fermat changed the

“adequation” to the e quality m 5 f

(c). Now, when f is

a polynomial, it is easy to calculate each of the terms

(c), f

(c), . . . . And of course it turns out that

ðcÞ.

Fermat and Descartes became embroiled in a dis-

pute over the tangent problem. It began with a letter of

January 18, 1638 in which Descartes attributed the

success of Fermat’s method to luck. When other French

mathematicians sided with Fermat, Descartes wrote

“I admire that [Fermat’s method] . . . has found

defenders; when M.D escartes will have understood

the method, then he will cease to admire only

that the method has found its defender s and also

admire the method itself.”

Descartes chose G

erard Desargues (1593 2 1662,

Lyon) to referee the dispute. In April of 1638, Desar-

gues concluded that, although Fermat’s method was

correct, his explanation was faulty and therefore “M.

des Cartes is right and M. de Fermat is not wrong.”

Descartes was still not persuaded: “His supposed

rule is not so general as he makes it seem, and it can be

applied only to the easiest problems, not to any ques-

tion which is the least bit difﬁcult.” With that Descartes

posed a challenge problem for Fermat: to ﬁnd the

tangent lines of x

5 nxy, a curve that is now known

as the Folium of Descartes. Descart es must have

expected that Fermat’s method would be as futile as his

own when applied to this curve. In fact, Fermat had not

the slightest difﬁculty (Figure 4). He quickly sent

Descartes a solution together with a revised explana-

tion of his method. Descartes conceded, not too

gracefully: “ . . . had you so explained [your method] in

the ﬁrst place, I would not have objected at all.” In fact,

Descartes continued to object in his correspondence

with others. “Is it not a great marv el,” he wrote, “that

in six months Fermat has found a ne w slant to justify

his method.” In a subsequent letter, Descartes des-

cribed Fermat’s tangent construction as “the most

f(c  h)

H  f (c)

f(c)

m Figure 3

(x  (c  h))

 y

 r

(

c  h, 0

)

P  (c, c)

y 

Slope  2



m Figure 2

276 Chapter

3 The Derivative

ridiculous gibberish.” By 1641, Descartes ﬁnally rea-

lized the futility of attacking the mathematics of Fer-

mat and switched tactics: “I believe that he [Fermat]

does know mathematics, but I still maintain that in

philosophy he reason s badly.”

Newton’s Method of Differentiation

So far, we have described the tangent problem only

from a geometric point of view. But the kinematic

viewpoint is also important. Among the early con-

tributors to the different ial calculus, Roberval and

Torricelli are noteworthy for being the ﬁrst to link the

tangent problem with the notion of instantaneous

velocity. To Sir Isaac Newton, that connection would

be fundamental.

The mathematical language of Newton has not, for

the most part, survived. Newton called the v ariables x

and y ﬂuents, imagini ng them to trace a curve by their

movement. The velocities of the ﬂuents were called

ﬂuxions and denoted by

x and

y. Newton’s inﬁnitesi-

mals were called moments of ﬂuxions and rep resented

xo and

yo where o is not 0 but an “inﬁnitely small

quantity.” To illustrate, let us use

Fðx; yÞ5 x

2 ax

1 axy 2 y

5 0;

the example given by Newton in his Methodus Flux-

ionum written in 1670. Newton substituted x 1

xo for x

and y 1

yo for y in the equation F(x, y ) 5 0. On

expanding the left side of the equation Fðx 1

xo;

y 1

yoÞ5 0, remembering that F(x, y) 5 0, we arrive at

ð3x

2 2ax 1 ayÞ

xo 1 ðax 2 3y

yo 1 a 

xo 

1 ð

xoÞ

ð3x 2 a 1

xoÞ2 ð

yoÞ

ð3y 1

yoÞ5 0:

Newton divided by o, obtaining

ð3x

2 2ax 1 ayÞ

x 1 ðax 2 3y

1 o



y 1

ð3x 2 a 1

xoÞ2

ð3y 1

yoÞ



5 0:

He then discarded all terms with o as a factor. In

his words,

“But whereas o is supposed to be inﬁni tely little . . . ,

the terms which are multiplied by it will be nothing

in respect to the rest. Therefore I reject them and

there remains: ð3x

2 2ax 1 ayÞ

x 1 ðax 2 3y

y 5 0.”

The result is that

2 2ax 1 ay

ax 2 3y

;

which is the slope of the tangent line.

Newton, like Fermat before him and Leibniz after

him, employed the su spect procedure of dividing by a

quantity that he would later take to be 0. Newton’s

attempt to explain this undesirable situation is not very

convincing. From his Principia of 1686, we ﬁnd:

“Those ultimate ratios with which quantities vanish

are not truly the ratios of ultimate quantities, but

limits toward which the ratio s of quantities, decreas-

ing without limit, do always converge, and to which

they approach nearer than by any given difference,

but never go beyond, nor in effect attain to, until the

quantities have diminished in inﬁnitum. Quantities,

and the ratio of quantities, which in any ﬁnite time

converge continually to equality, and before the end

of that time approach neare the one to the other than

by any given difference, become ultimately equal.”

Bishop Berkeley, the critic quoted in Genesis and

Development 2, had this to say in respon se:

“The great author of the method of ﬂuxions felt this

difﬁculty and therefore he gave in to those nice

abstractions and geometrical metaphysics without

which he saw nothing could be done on the received

principles . . . It must, in deed, be acknowledged that

he used ﬂuxions like the scaffold of a building, as

things to be laid aside or got rid of . . . And what are

these ﬂuxions? . . . They are neither ﬁnite quantities

nor quantities inﬁnitely small, nor yet nothing. May we

not call them the ghosts of departed quantities . . . ?”

As we have described in Genesis and Development 2,

this controversy eventually led to the formalization of

the limit concept.

 y

 nxy

m Figure 4

Genesis & Development 277

The Product Rule and the Chain Rule

The rules of differential calculus that have been pre-

sented in this chapter were developed by Newton and,

independently, at a later date, by Leibniz. The Product

Rule, for example, appeared in Leibniz’s work as d

(xυ) 5 xd υ1υdx. Leibniz obtained this equation by

treating d(xυ) as the inﬁnitesimal increment in xυ that

arises by incrementing x by dx and υ by dυ. He then

discarded the second order inﬁnitesimal dx dυ that

arises in the calculation. Thus

dðxυÞ5 ðx 1 dxÞðυ 1 dυÞ2 xυ 5 xυ 1 xdυ 1 υdx

1 ðdxdυÞ2 xυ 5 xdυ 1 υdx:

Leibniz introduced the notation dx in a manuscript of

11 November 1675. In that manuscript, Leibniz strug-

gled to obtain the rules of differential calculus such as

the Product Rule. It is not easy to determine Leibniz’s

progress on that particular day. His initial guess was that

d(xυ) 5 dx dυ. By the end of the manuscript, he seems

to have been aware of the incorrectness of his con-

jecture. His initial guess for the Quotient Rule was also

wrong. But, by the end of November 1675, Leibniz had

discovered a correct calculus of differentials.

Newton evidently felt constrained to account for

the dx

dυ term that Leibniz simply discarded. He

offered the following demonstration (which we have

converted into Leibniz’s inﬁnitesimal notation):

dðxυÞ5



x 1



υ 1

dυ





x 2



υ 2

dυ



5 xυ 1

xdυ 1

υ dx 1

dx dυ 2 xυ 1

xdυ

υ dx 2

dx dυ

5 xdυ 1 υ dx:

Berkeley speciﬁcally cited this derivation as an

example of Newton’s mathematical sleight of hand. In

1862, Sir William Rowan Hamilton (1805  1865,

Dublin), himself a major ﬁgure in the development of

calculus and physics, was also troubled by this

computation:

“It is very difﬁcult to understand the logic by which

Newton proposes to prove [the Product Rule]. His

mode of getting rid of [dxdυ] appeared to me . . . to

involve so much artiﬁce, as to deserve to be called

sophistical . . . But by what right or by what reason

other than to give an unreal air of simplicity to the

calculation does he prepare the products thus? . . . it

quite masks the notion of a limit . . . Newton does

not seem to have cared for being very consistent

in his philosophy, if he could anyway get hold of

truth . . . ”

In the early 1900s, Constantin Carath

eodory (1873,

Berlin 2 1950, Munich) developed differential calculus

in such a way that the standard rules be came particu-

larly easy to prove. Following Carath

eodory’s

approach, f is said to be differentiable at c if and only if

there is a function Φ

that is continuous at c such that

f ðxÞ5 f ðcÞ1 ðx 2 cÞΦ

ðxÞ:

The derivative of f at c is then deﬁned by f

ðcÞ5 Φ

(c).

Let us use this interpretation of the derivative to derive

two theorems whose proofs we deferred.

Proof of the Product Rule

Suppose that f and g are differentiable at c. Thus there

are continuous funct ions Φ

and Φ

such that

f ðxÞ5 f ðcÞ1 ðx 2 cÞΦ

ðxÞ

and gðxÞ5 gðcÞ1 ðx 2 cÞΦ

ðxÞ:

Therefore

ðf  gÞðxÞ5 f ðxÞgðxÞ



f ðcÞ1 ðx 2 cÞΦ

ðxÞ



gðcÞ1 ðx 2 cÞΦ

ðxÞ



5 f ðcÞgðcÞ1 ðx 2 cÞf ðcÞΦ

ðxÞ

1 ðx 2 cÞgðcÞΦ

ðxÞ1 ðx2 cÞ

 Φ

ðxÞΦ

ðxÞ

5 ðf  gÞðcÞ1 ðx 2 cÞ



f ðcÞΦ

ðxÞ1 gðc ÞΦ

ðxÞ1 ðx 2 cÞΦ

ðxÞΦ

ðxÞ



Because the function

f g

ðxÞ5 f ðcÞΦ

ðxÞ1 g ðcÞΦ

ðxÞ1 ðx 2 cÞΦ

ðxÞΦ

ðxÞ

is continuous, it follows that f g is differentiable and

ðf  gÞ

ðcÞ 5 Φ

f  g

ðcÞ

5 f ðcÞΦ

ðcÞ1 gðcÞΦ

ðcÞ

1 ðc 2 cÞΦ

ðcÞΦ

ðcÞ

5 f ðcÞg

ðcÞ1 gðcÞf

ðcÞ:

Proof of the Chain Rule

Recall that the Chain Rule asserts that if f is differ-

entiable at c and if g is differentiable at f (c), then g 3 f

is differentiable at c and ðg 3 f Þ

ðcÞ5 g

ðf ðcÞÞ  f

ðcÞ.

278 Chapter 3 The Derivative

Assuming the stated differentiability hypotheses for f

and g, there are continuous functions Φ

and Φ

such

that

f ðxÞ5 f ðcÞ1 ðx 2 cÞΦ

ðxÞ; f

ðcÞ5 Φ

ðcÞ

and

gðxÞ5 gðf ðcÞÞ1 ðx 2 f ðcÞÞ  Φ

ðxÞ; g

ðf ðcÞÞ5 Φ

ðf ðcÞÞ:

Therefore

gðf ðxÞÞ 5 gðf ðcÞÞ1 ðf ðxÞ2 f ðcÞÞ  Φ

ðf ðxÞÞ

5 gðf ðcÞÞ1 ððx 2 cÞΦ

ðxÞÞ  Φ

ðf ðxÞÞ

5 gðf ðcÞÞ1 ðx 2 cÞðΦ

ðxÞðΦ

3f ÞðxÞÞ:

Because x/Φ

(x) (Φ

3 f )(x) is continuous at c,it

follows that g 3 f is differentiable at c and that

ðg 3 f Þ

ðcÞ5 Φ

ðcÞðΦ

3 f ÞðcÞ

5 Φ

ðf ðcÞÞ  Φ

ðcÞ5 g

ðf ðcÞÞ  f

ðcÞ:

Genesis & Development 279

This page intentionally left blank

CHAPTER 4

Applications of the

Derivative

The need to maximize and minimize functions often arises in science, engineering,

and commerce. For example, a company developing a new product might want

to maximize its proﬁt. An ecologist might want the company to minimize its

consumption of resources. In sho rt, procedures for optimizing functions are among

the most vital applicat ions of mathematics. In this chapter, we will see that the

derivative provides a powerful tool for analyzing the extreme values of functions.

We will learn that, to maximize or minimiz e a differentiable function f,we

must ﬁrst ﬁnd the roots of the equation f

(x) 5 0. Solving such an equation can

present formidable difﬁculties, but, here too, the de rivative can be an essential aid.

In this chapter, we will learn that differential calculus provides a method for

approximating the roots of equations.

One of the main considerations of the present chapter will be the use of the

derivative as an aid in sketching the graph of a function. We will learn to combine

several applications of the derivative to sketch the graphs of functions. Graphing

calculators and software are certainly useful tools, but they are not a substitute for

this knowledge.

PREVIEW

281

4.1 Related Rates

In a related rates problem, two variables are related by means of an equation.

When one variable changes, so must the other to satisfy the equation. The question

we study in this section is, How can we use the rate of change of one variable to

calculate the rate of change of the other variable?

The Role of the Chain

Rule in Related Rates

Problems

In the most basic related rates problem, two variables x and y are related by a

function: y 5 g (x). If x depends on a third variable t, then so does y through the

equation y 5 g (x). The Chain Rule tells us the relationship between the rates of

change of x and y with respect to t:

⁄ EX

AMPLE 1 If a train that is approaching a platform with speed s (mea-

sured in m/s) sounds a horn with frequency 500 Hz, then, according to the Doppler

effect, the frequency ν heard by a stationary observer on the platform is

ν 5 500 



345

345 2 s



Hz:

If the train is decelerating at a constant rate of 4 m/s

, what is the rate of change of

ν when the train’s speed is 25 m/s?

Solution

1. The quantities involved are the variables ν and s.

These are functions of time t.

2. The relationship between the variables is expressed by the equation

ν 5 500 345/(345 2 s) 5 172500/(345 2 s). In this example, one variable, ν,has

been given explicitly in terms of the other.

3. We implicitly differentiate with respect to t. Using the Chain Rule and the

Reciprocal Rule, we calculate

dν

5 172500



345 2 s



5 172500



345 2 s



52172500

ð345  sÞ

ð345 2 sÞ



172500

ð345 2 sÞ



4. We substitute the given data into the formula for dν/dt that we obtained in

Step 3. We ﬁnd that, when s 5 25 and ds/dt 524, the rate of change dν/dt of the

observed frequency, in Hz/s, is

dν

172500

ð3452 25Þ

ð24Þ52

1725

256

 26:74: ¥

The Role of Implicit

Differentiation

The Method of Implicit Differentiati on is used to solve related rates problems in

which two variables x and y are related by an equation

Fðx; yÞ5 C; ð4:1:1Þ

282 Chapter 4 Applications of the Derivative

where C is a constant. Each side of equation (4.1.1) is differentiated with respect to

t. After differentiation, the right side of the equation is 0, and the left side is an

expression involving x, y, dx/dt, and dy/dt. We may write this last equati on as



x; y;

;



5 0: ð4:1:2Þ

Typically, one of the derivatives, dx/dt or dy/dt, is speciﬁed, and the other must be

determined from equation (4.1.2). To do so, it may be necess ary to use equation

(4.1.1) if the value of only one of the variables, x or y, has been speciﬁed. The next

example will illustrate these ideas.

⁄ EX

AMPLE 2 Suppose that y

1 xy 2 4x 5 0. If x 5 4 and dx/dt 5 3 when

t 5 5, what is dy/dt when t 5 5?

Solution

1. The quantities involved are the variables x an

d y. These are functions of time t.

2. The relationship between the variables is expressed by the equation y

1 xy 2

4x 5 0. We can use the form that has been given without explicitly solving for

one variable in terms of the other.

3. We implicitly differentiate with respect to t. Using the Chain Rule-Pow er Rule

for the term y

and the Product Rule and Chai n Rule for the term xy, we obtain



 y 1 x



2 4

5 0: ð4:1:3Þ

(The left side of eq uation (4.1.3) is the expression G (x, y, dx/dt, dy /dt) to which

we referred in the general discussion.)

4. We know that, at t 5 5, we have dx/dt 5 3 and x 5 4. To use the equation

obtained in Step 3, we also need to know the value of y at t 5 5. To determine

this value, we turn to the given equation y

1 xy 2 4x 5 0 and substitute x 5 4.

We obtain y

1 4y 2 16 5 0, or (y 2 2) (y

1 2y 1 8) 5 0, or y 5 2. We now sub-

stitute all known values into equation (4.1.3) of Step 3:

3ð2Þ



ð3Þð2Þ1 ð4Þ



2 4ð3Þ5 0:

Solving for dy/dt, we obtain dy/dt 5 3/8.

INSIGHT

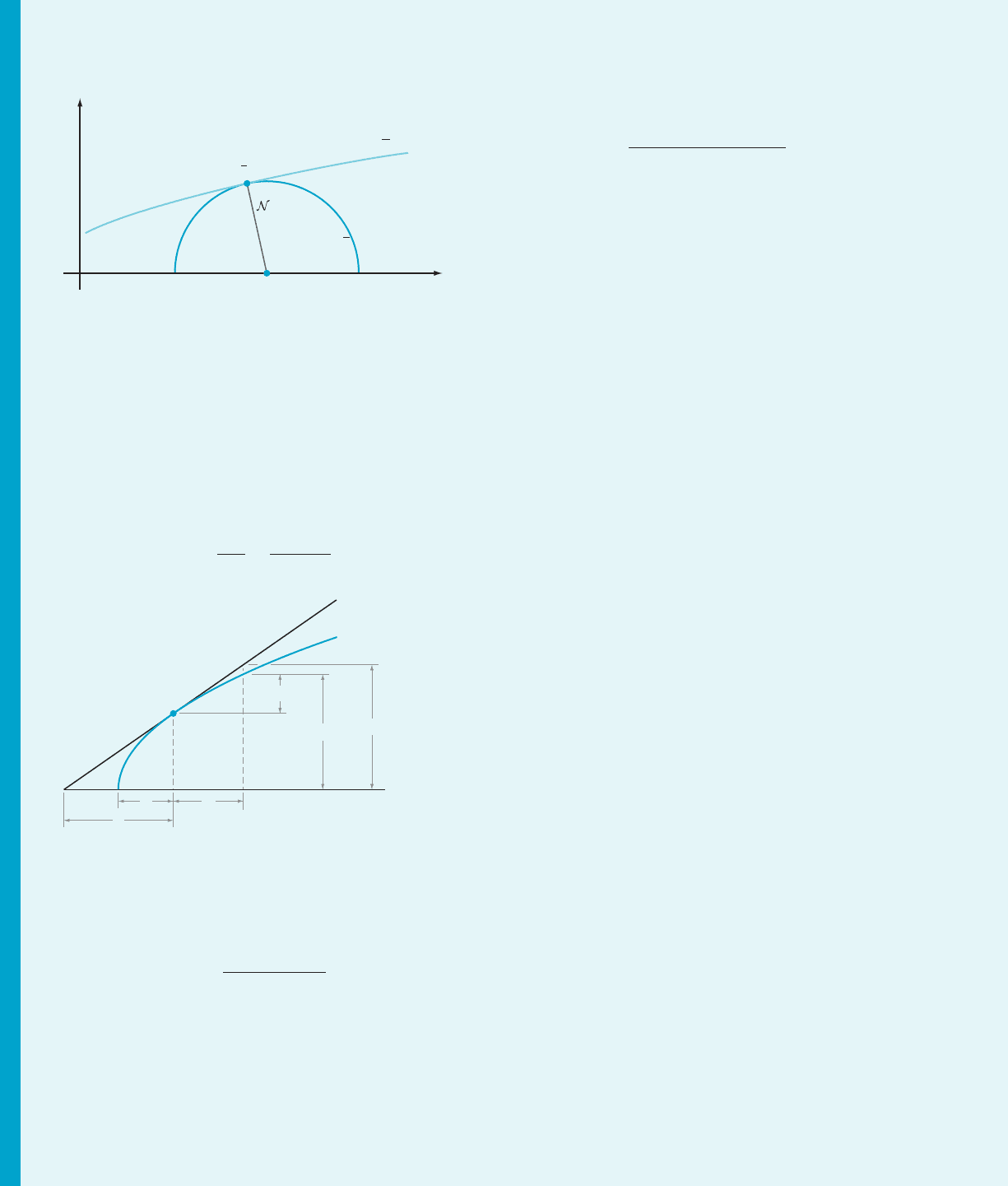
Figure 1 shows the plot of the graph C of the equation y

1 xy 2 4x 5 0from

Example 2 in the viewing rectangle [1/4, 8] 3 [3/4,2.5].Wemaythinkofaparticlemoving

upward and to the right along C with position (x, y)attimet. From this point of view, the

variable t is a parameter for C.Whent is equal to 5, the particle passes through the point

5 (4, 2). Because explicit parametric equations for x and y are not given, the value 5 of t is

used only as a way of referring to P

. Had the particle passed through P

at a different time

such as 7, or even at an unspeciﬁed instant t

, the calculations would have been exactly the

same. Formula (3.8.9) in Chapter 3 tells us that the slope of the tangent line to C at P



dy=dtj

t55

dx=dtj

t55

3=8

The equation of the tangent line to C at P

is therefore y 5 (1/8) (x 2 4) 1 2, and the line

described by this equation is also plotted in Figure 1.

1.5

2468

 (4, 2)

2.5

y  (x  4)  2

m Figure 1

4.1 Related Rates 283

⁄ EXAMPLE 3 The relationship between pressure P (measured in atmo-

spheres) and volume V (measured in liters) of 1 mole of carbon dioxide at 0



c is

approximated by van der Waal’s equation



P 1



ðV 2 bÞ5 22:40;

where a 5 3.592, and b 5 0.04267. At a certain time t

, the volum e V of a carbon

dioxide sample is 4 liters, and the pressure is increasing at the rate of 0.1 atmo-

sphere per second. At what rate is V de creasing when t 5 t

Solution

1. The quantities involved are the pressure P and

the volume V. These are func-

tions of time t.

2. The relationship between the variables is expressed by van der Waal’s equation.

We can use the form that has been given without explicitly solving for one

variable in terms of the other.

3. We implicitly differentiate with respect to t. Using the Product Rule, we obtain



2 2



ðV 2 bÞ1



P 1



5 0:

4. We know that at t

, dP/dt 5 0.1 and V 5 4. The constants a and b are given. To

use the equation obtained in Step 3, we also need to know the value of P at t

We use van der Waal’s equation to determine the value of P:



P 1

3:592



ð4 2 0:04267 Þ5 22:40

or P 5 5.436. We now substitute all known values into the equation of Step 3:



0:1 2 2

3:592



ð4 2 0:04267 Þ1



5:436 1

3:592



5 0:

We solve for dV/dt, obtaining dV/dt 527.586 3 10

liters per second. Thus the

volume of the carbon dioxide sample is decreasing at the rate of 7.586 3 10

liters per second. ¥

Basic Steps for Solving

a Related Rates

Problem

The analysis that enabled us to solve Examples 13 can be systematized as follows:

1. Identify the quantities that are varying, and identify the variable (this is often

“time”) with respect to which the change in these quantities is taking place.

2. Establish a relationship (an equation) between the quantities isolated in Step 1.

3. Differentiate the equation from Step 2 with respect to the variable identiﬁed in

Step 1. Be sure to apply the Chain Rule carefully.

4. Substitute the numerical data into the equation from Step 3, and solve for the

unknown rate of change.

We will consider two more examples that illustrate this approach.

⁄ EX

AMPLE 4 A sample of a new polymer is in the shape of a cube. It is

subjected to heat so that its expansion properties may be studied. The surface area

of the cube is increasing at the rate of 6 square inches per minute. How fast is the

volume increasing at the moment when the surface area is 150 square inches?

284 Chapter 4 Applications of the Derivative