Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Solution The primary interest of this example is that surface area and volume are

related indirectly. We use the Chain Rule, but we do not have to differentiate

implicitly.

1. The functions are surface area A and

volume V. It is useful to introduce the

function s for side length because A and V are related by means of s. The

variable is time t .

2. We have V 5 s

and A 5 6s

. (The last equation arises because a cube has six

faces, each with area s

3. We differentiate both the equations from Step 2 with respect to the variable t.

Thus

5 3s



and

5 6  2s 

We use the second of these equations to solve for ds/dt:

12s







We substitute this expression for ds/dt into the equation that we obtained for

dV/dt:

5 3s





12s









4. We notice that, at the instant with which the problem is concerned, A 5 150,

hence s 5 5. Also, dA/dt 5 6. Substituting this information into the last equation

in Step 3 gives

 6 5

ðcu: in:Þ=min:

The volume of the cube of polymer is expanding at the rate of 15/2 cubic inches

per minute at the moment in question.

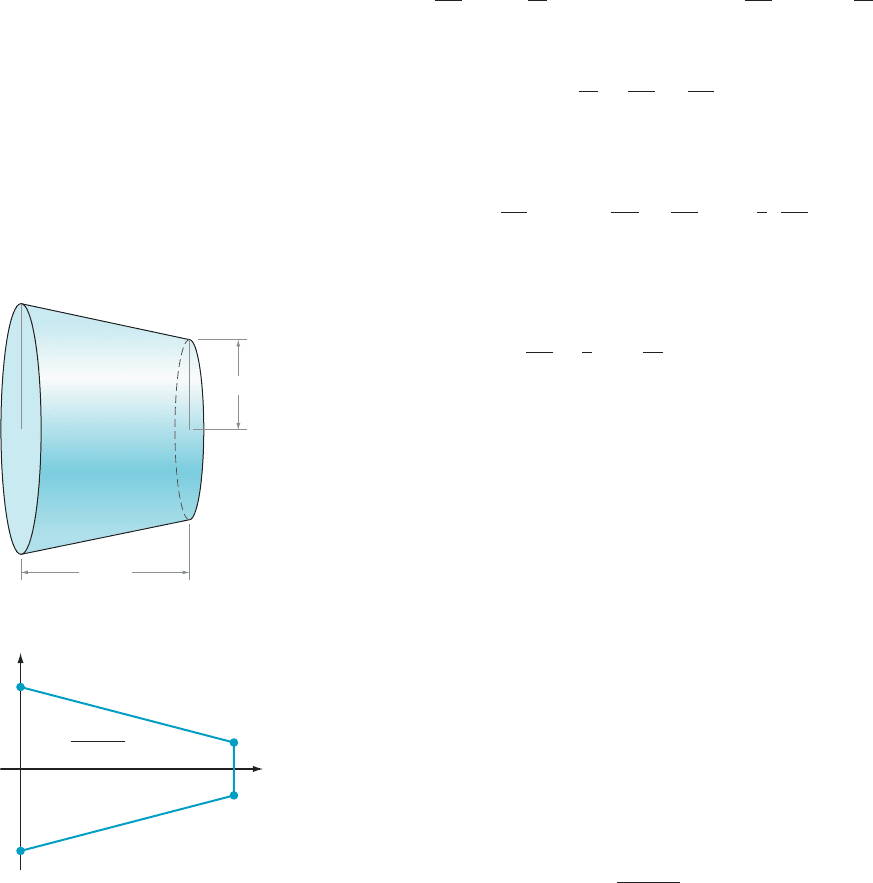
⁄ EXAMPLE 5 (An Application to Biology) A blood vessel is slightly

tapered in shape, like a truncated cone, as illustrated in Figure 2. The effect of a

certain pain-relieving drug is to increase the larger radius at the rate of 0.01

millimeter per minute. During this expansion process, the length of the blood vessel

remains ﬁxed at 40 millimeters, and the smaller radius remains ﬁxed at 0.5 milli-

meters. At the moment when the larg er radius is 2 millimeters, how is the volume

of the blood vessel changing?

Solution

1. The functions involved in this problem are the larger radius R and

the volume of

the blood vessel V. The variable is t.

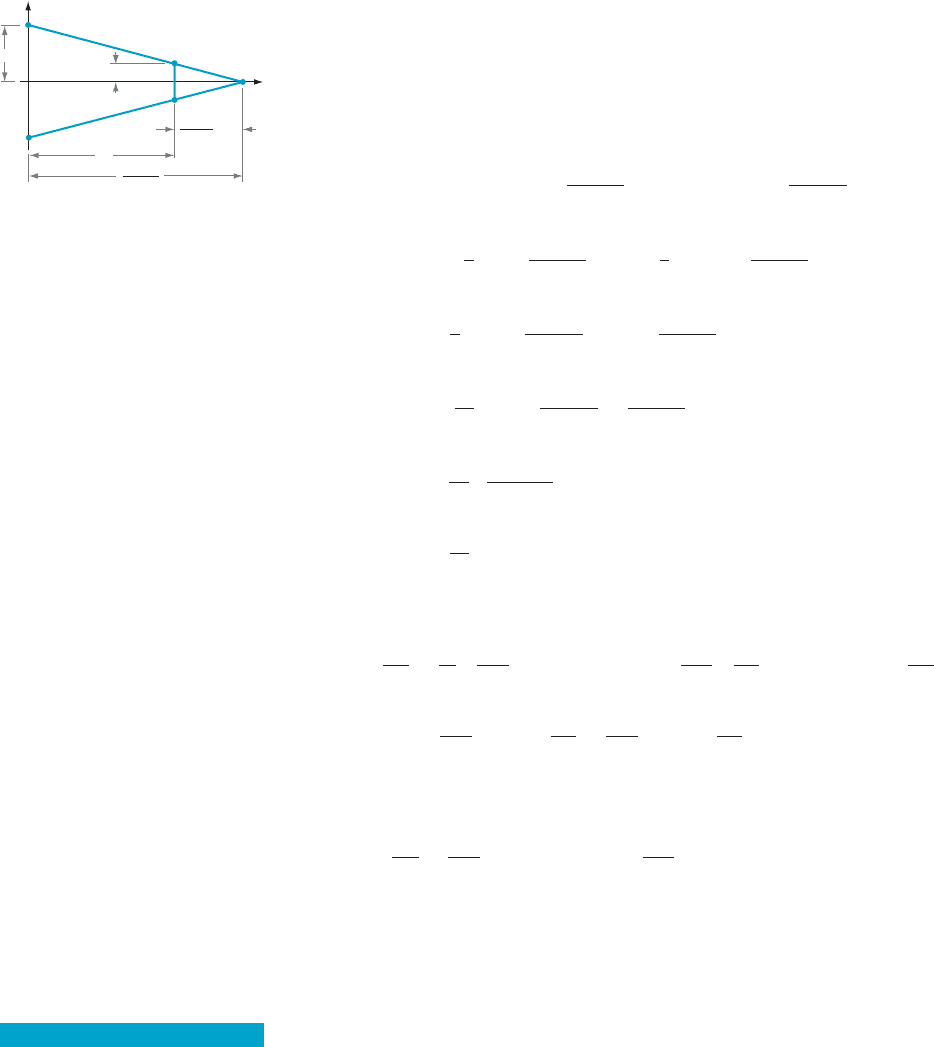
2. To calculate the volume of the blood vessel for a given R, we use the cross-

sectional diagram in Figure 3. The edge of the blood vessel is given by a line of

slope (R 2 0.5)/(0 2 40) and y-intercept R. From this information, we see that the

slope-intercept equation of the line is

y 5



R 2 0:5

240



x 1 R:

0.5 mm

40 mm

m Figure 2

(0, R)

(40, 0.5)

y 

x  R

R  0.5

40



m Figure 3

4.1 Related Rates 285

Substituting y 5 0 in this equation and solving for x, we ﬁnd that the line has

x-intercept 40R/(R 2 0.5), or 80R/(2R 2 1). From Figure 4, we see that

V 5

volume of cone with

radius 5 R;

height 5

80R

2R 2 1

volume of cone with

radius 5 0:5;

height 5

80R

2R 2 1

2 40



πR



80R

2R 2 1





πð0:5Þ



80R

2R 2 1

2 40







80R

2R 2 1

2 0:25 

2R 2 1







2R 2 1



2 1

2R 2 1

πð4R

1 2R 1 1Þðby long division of polynomialsÞ:

3. We may now differentiate V with respect to t. Doing so, we obtain



10π

ð4R

1 2R 1 1Þ



10π



ð4R

1 2R 1 1Þ



10π

ð8R 1 2Þ

20π

ð4R 1 1Þ

4. We substitute the values R 5 2 and dR/dt 5 0.01 to obtain

20π

ð4  2 1 1Þð0:01Þ5

20π

ð9Þð0:01Þ5 60πð0:01Þ5 0:6π:

Thus the volume of the blood vessel is increasing at the rate of 0.6π cubic

millimeters per mi nute.

QUICK QUIZ

1. Suppose that y 5 x

, x 5 2, and dy/dt 5 60 when t 5 10. What is dx/dt when

t 5 10?

2. Suppose that x and y are positive variables, that 2x 1 y

5 14, that x is a function

of t, and that dx/dt 5 4 for all t . What is dy/dt when x 5 3?

Answers

1. 5 2. 22/3

(0, R)

(40, 0.5)

0.5

80R

2R  1

80R

2R  1

 40

m Figure 4

286 Chapter

4 Applications of the Derivative

EXERCISES

Problems for Practice

c In each of Exercises 126, the variable y is given as a

function of x, which depends on t. The values x

and v

of,

respectively, x and dx/dt are given at a value t

of t. Use this

data to ﬁnd dy/dt at t

. b

y 5 x

; x

5 2; v

5 5

y 5 x

2 2x; x

5 2; v

523

3. y 5 cosðxÞ; x

5 π=6; v

522

y 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2x 2 1

; x

5 5; v

5 7

5. y 5 x lnð2xÞ; x

5 1=2; v

5 3

y 5 x

3=2

2 expð22xÞ; x

5 1; v

5 4

c In each of Exercises 7210, the variable y is

given as a

function of x, which depends on t. The values y

and s

of,

respectively, y and dy/dt are given at a value t

of t. Use this

data to ﬁnd dx/dt at t

. b

7. y 5 14 2 11x; y

5 12; s

5 22

y 5 x

; y

528; s

5 5

9. y 5 6 exp ð23xÞ; y

5 6; s

5 54

10.

y 5 4x 1 sin

ðxÞ; y

5 π 1 1=2; s

5 30

c In each of Exercises 11216, variables x and y,

which

depend on t, are related by a given equation. A point P

the graph of that equation is also given, as is one of the fol-

lowing two values:



or s



Find the other. b

11.

1 y

5 3; P

5 ð2; 21Þ; v

5 3

12.

1 y

5 3; P

5 ð22; 3Þ; v

5 2

13.

1 xy 5 2; P

5 ð22; 1Þ; s

5 3

14.

ﬃﬃﬃ

ﬃﬃﬃﬃﬃ

5 1; P

5 ð4; 3Þ; s

5 5

15.

2 x

y 1 3y 5 13; P

5 ð2; 3Þ; v

522

16.

1 x expðyÞ1 y 5 6; P

5 ð2; 0Þ; s

521

c In each of Exercises 17222,

variables x and y are functions

of a parameter t and are related by a given equation. A point

on the graph of that equation is also given, as is one of the

following two values:



or s



Find the other value. Also, referring to the Insight that fol-

lows Example 2, ﬁnd the tangent line to the graph of the given

equation at P

. b

17.

1 y

5 9; P

5 ð21; 2Þ; v

5 3

18.

1 y

5 8; P

5 ð2; 22Þ; v

521

19.

2 xy 5 1; P

5 ð1; 2Þ; s

522

20.

2x 2

ﬃﬃﬃ

5 3; P

5 ð4; 9Þ; s

5 2

21.

2 xy

1 lnðy=2Þ5 6; P

5 ð3; 2Þ; v

522

22.

2 3x expðyÞ1 y 5 10; P

5 ð22; 0Þ; s

521

23. The diagonal of a square is increasing at a rate of 2

inches per minute. At the moment when the diagonal

measures 5 inches, how fast is the area of the square

increasing?

24. The length of each leg of an isosceles right triangle

is increasing at the rate of 2 mm/s. How fast is the

hypotenuse increasing at the moment when each leg is

10 mm?

25. The side length of an equilateral triangle is decreasing at

the rate of 3 cm/s. How fast is the area decreasing at the

moment when the area is 27

ﬃﬃﬃ

26. The volume of a cube is increasing at the rate of 60 mm

/s.

How fast is the surface area of the cube increasing when

each edge is 20 mm?

27. Let P denote the position of particle that, from its initial

point Q 5 (1, 0), moves counterclockwise along the unit

circle. If θ denotes the angle subtended at the origin O by

the circular arc QP, then the radial velocity dθ/dt of the

particle is constantly equal to 6. How fast is the area of

the sector QPO swept out by the particle changing?

28. If an airplane climbs at 550 mph making a π/6 angle with

the horizontal, how fast is it gaining altitude?

29. A container is pulled up a 10 ft long ramp fro m the ground

to a loading dock 4 ft above the ground. At the moment it is

halfway along the ramp, it is moving at the rate of 1.2 ft/s.

How fast is it rising at that instant?

30. A rocket that is rising vertically is being tracked by a

ground-level camera located 3 mi from the point of blast-

off. When the rocket is 2 mi high, its speed is 400 mph. At

what rate is the (acute) angle between the horizontal and

the camera’s line of sight changing?

31. A spherical balloon is losing air at the rate of 6 cm

/min.

At what rate is its radius r decreasing when r 5 24 cm?

32. A spherical balloon is inﬂated so that its volume increases

at the rate of 6 cm

/min. How fast is the surface area of

the balloon increasing when r 5 24 cm?

33. Suppose that grain pouring from a chute forms a conical

heap in such a way that the height is always 2/3 the radius

of the base. At the moment when the conical heap is 3 m

high, its height is rising at the rate of 1/2 m/min. At what

rate (in m

/min) is the grain pouring from the chute?

34. Particle A moves down the x-axis in the positive direction

at a rate of 5 units per second. Particle B walks up the

y-axis in the positive direction at a rate of 8 units per

second. At the moment when A is at (4, 0) and B is at

(0, 9), how rapidly is the distance between A and B

changing?

35. A policeman stands 60 feet from the edge of a straight

highway while a car speeds down the highway. Using a

radar gun, the policeman ascertains that, at a particular

instant, the car is 100 feet away from him and the distance

between himself and the car is changing at a rate of 92

4.1 Related Rates 287

feet per second. At that moment, how fast is the car

traveling down the highway?

36. A 5 foot, 10 inch tall woman is walking away from a wall

at the rate of 4 ft/s. A light is attached to the wall at a

height of 10 feet. How fast is the length of the woman’s

shadow changing at the moment when she is 12 feet from

the wall?

37. A spherical raindrop is evaporating. Suppose that units

are chosen so that the rate at which the volume decreases

is numerically equal to the surface area. At what rate does

the radius decrease?

38. A lighthouse is 100 feet tall. It keeps its beam focused on

a boat that is sailing away from the lighthouse at the rate

of 300 feet per minute. If θ denotes the acute angle

between the beam of light and the surface of the water,

then how fast is θ changing at the moment the boat is 1000

feet from the lighthouse?

39. A particle moves around the curve x

1 2y

5 25 in such a

way that dy/dt 5 y. What is the rate of change of the

particle’s x-coordinate at the moment when x 5 3?

Further Theory and Practice

40. A spherical balloon is being inﬂated. At a certain instant

its radius is 12 cm and its area is increasing at the rate of

24 cm

/min. At that moment, how fast is its volume

increasing?

41. A conical tank ﬁlled with water is 5 m high. The radius of

its circular top is 3 m. The tank leaks water at the rate

of 120 cm

/min. When the surface of the remaining water

has area equal to π m

, how fast is the depth of the

water decreasing?

42. A particle moves along the curve y 5

ﬃﬃﬃ

in an xy-plane in

which each horizontal unit and each vertical unit repre-

sents 1 cm. At the moment the particle passes through the

point (4, 2), its x-coordinate increases at the rate 7 cm/s.

At what rate does the distance between the particle and

the point (0, 5) change?

43. If R

and R

are parallel variable resistances, then the

resulting resistance R satisﬁes 1/R 5 1/R

1 1/R

.IfR

increases at the rate of 0.6 Ω/s when R

5 40 Ω, and

5 20 Ω, then at what rate must R

decrease if R

remains constant? (The unit by which resistance in an

electric circuit is usually measured, the ohm, is denoted

by Ω.)

44. At 1 PM, a car traveling east at a constant speed of 30 mph

passes through an intersection. At 2 PM, a car traveling

south at a constant speed of 40 mph passes through the

same intersection. How fast is the distance between the

two cars changing at 3 PM?

45. A particle moves along the curve y 5

ﬃﬃﬃ

. At what point are

the rates of change of the particle’s coordinates equal?

46. In a hemispherical tank of radius 20 feet, the volume of

water is πh

(60 h)/3 cubic feet when the depth is h feet

at the deepest point. If the water is draining at the rate of

5 cubic feet per minute, how fast is the area of the water

on the surface decreasing when the water is 10 feet deep?

47. When heated, the height of a certain solid cylindrical rod

increases at twice the rate at which the radius increases. If

the volume increases at the constant rate of 60π cm

/min,

at what rate is the radius increasing when r 5 3 cm and

h 5 17 cm?

48. The demand curve for a given commodity is the set of all

points ( p, q) in the pq-plane where q is the number of

units of the product that can be sold at price p. The

elasticity of demand for the product at price p is deﬁned to

be E (p) 52q

(p) p/q (p).

a. Suppose that a demand curve for a commodity is

given by

p 1 q 1 2p

q 1 3pq

5 1000

when p is measured in dollars and the quantity q of

items sold is measured by the 1000. For example, the

point (p, q) 5 (6, 3.454) is on the curve. That means

that 3454 items are sold at $6. What is the slope of the

demand curve at the point (6, 3.454)?

b. What is elasticity of demand for the product of part at

p 5 $6?

49. If a volume V

of oil spills from a tanker at sea, then there

are positive constants t

and h

such that, for t $ t

, the spilled

oil spreads as a cylindrical disk of height h (t) 5 h

ﬃﬃ

. Show

that, for t . t

, the radius r (t)ofthisdisksatisﬁes

ðtÞ5

3=4

ﬃﬃﬃﬃﬃﬃﬃﬃ

πh

50. The heat index is the apparent temperature T (



F) that a

human feels. A rough aproximation of T in terms of

actual temperature x (



F) and relative humidity h, where

h is a number in the interval [0, 100], is T 5 2.7 1 0.885x 2

0.787h 1 0.012xh. Suppose that the actual temperature is

increasing at the rate of 1.7



F/hr at the moment x 5 88

and h 5 60. How fast must humidity decrease for the heat

index to be unchanged?

51. The radius of a certain cone is increasing at a rate of 6

centimeters per minute while the height is decreasing at a

rate of 4 centimeters per minute. At the instant when the

radius is 9 centimeters and the height is 12 centimeters,

how is the volume changing?

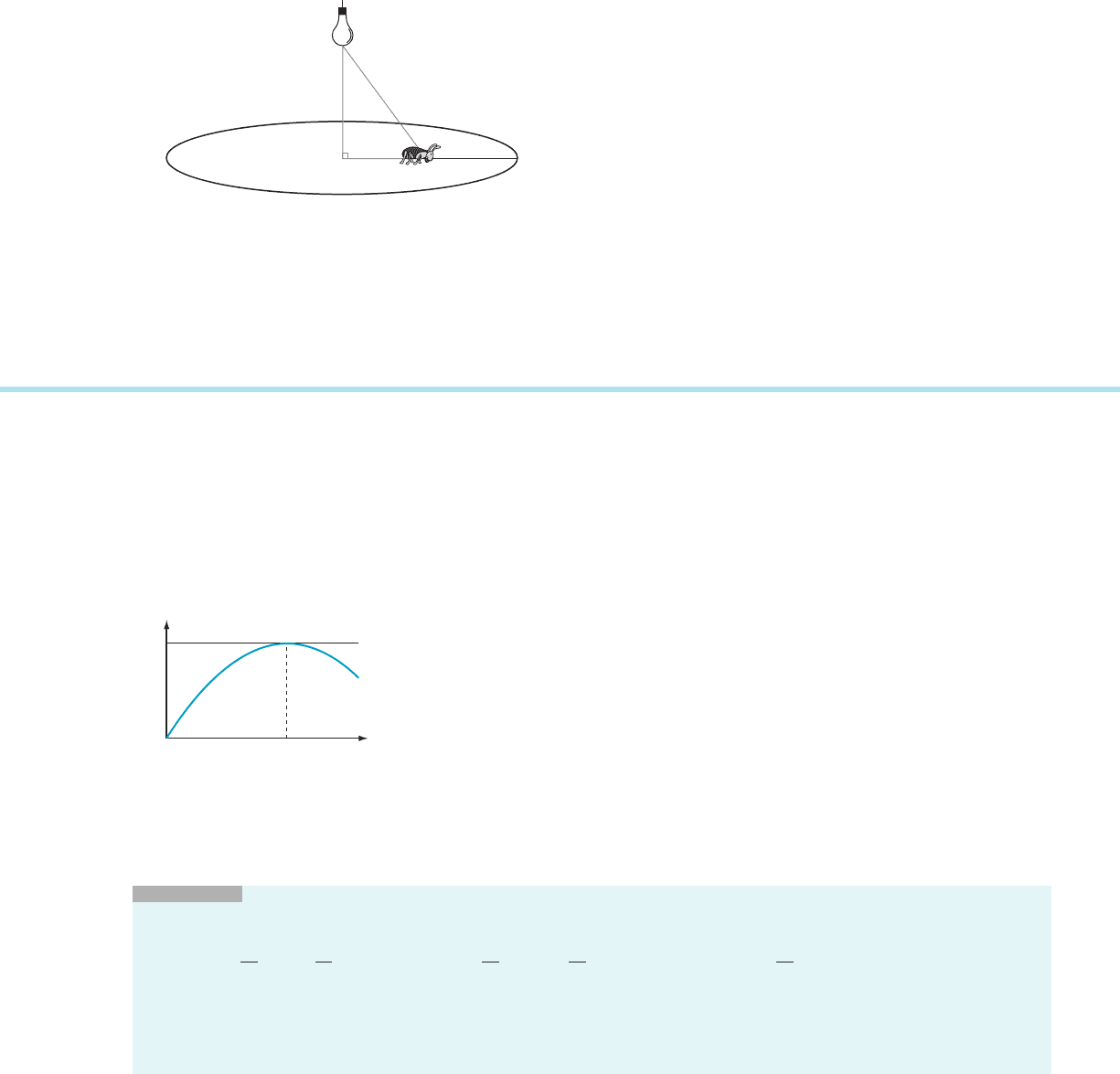
52. Under the cover of darkness, a bug has made its way to

the center of a round table of radius 2/3 m. Suddenly, a

light 4/3 m directly over the bug is switched on. The sur-

prised bug scampers in a direct line toward the edge of

the table at the rate of 12 cm/s. When the distance

between the bug and the light bulb is z meters, the

intensity I of illumination is given by I 5 120 cos (θ)/z

(see Figure 5). At what rate is I decreasing when the bug

reaches the edge of the table?

288 Chapter 4 Applications of the Derivative

Calculator/Computer Exercises

53. The sum of the volumes of a cube and a ball is, and

remains, 24000 cm

. The radius of the ball increases at a

rate of 2 cm/s. At the moment when the diameter is 26 cm,

how fast is the side length of the cube decreasing?

54. An approximation of the heat index T in terms of actual

temperature x (



F) and relative humidity h, where h is a

number in the interval [0, 100], is

T 5242:4 1 2:05x 1 10:1h 2 0:225 xh2 6:84  10

2 5:48 10

 h

1 1:23 10

 x

1 8:53  10

2 1:99  10

(See Exercise 50 for a simpler approximation.) Suppose

that the actual temperature is increasing at the rate of

1.7



F/hr at the moment x 5 88 and h 5 60. How fast must

humidity decrease for the heat index to be unchanged?

4.2 The Mean Value Theorem

In this section, we begin to investigate the properties of the graph of a function f

that can be deduced from the derivative f

. Our ﬁrst example is simple enough to be

analyzed without calculus. It will, however, suggest ways in which powerful

methods of calculus can be used to understand more complicated functions.

⁄ EX

AMPLE 1 Population biologist Raymond Pearl observed that the mass

x of a yeast culture grows at the rate R (x) 5 k x (2c 2 x), where c and k are

positive constants. For what value of the mass x is its rate of change R (x) greatest?

Solution Figure

1 shows the graph of y 5 R (x). Because R (x) is a quadratic

expression in x, we may complete the square as follows:

RðxÞ 5 k  x ð2c 2 xÞ

5 kc

2 kðc

2 2cx 1 x

5 kc

2 kðx 2 cÞ

Because k (x 2 c)

. 0 for x 6¼c, we see that

RðxÞ5 kc

2 kðx2cÞ

, kc

2 0 5 kc

5 RðcÞ for x 6¼ c:

Thus the maximum value of R (x) is attained when x 5 c.

INSIGHT

In Example 1, the tangent line to the graph of R at (c, R (c)) appears to be horizontal, or, equivalently, has zero

slope (see Figure 1). Indeed, we calculate that

RðxÞ5



2 kðx 2 cÞ



ðkc

Þ2 k

ðx 2 cÞ

5 0 2 k  2ðx 2 cÞ

ðx 2 cÞ522kðx 2 cÞ;

which is zero for x 5 c. We see that the maximum value of R ( x) occurs at precisely the value of x at which R

(x) is zero. What

we have just observed is not a coincidence: In this section, we will learn why the maximum value of a differentiable function is

located at a point where its derivative vanishes.

y  R(x)

R(c)

m Figure 1

m Figure 5

4.2 The Mean Value Theorem 289

Maxima and Minima To use the derivative for identifying maximum and minimum values of a function,

we must ﬁrst develop an appropriate notion of maximum and minimum. Remember

that f

expect f

DEFINITION

Let f be a function with domain S. We say that f has a local

maximum at the point c in S if there is a δ . 0 such that f (x) # f (c) for all x in S

such that |x 2 c| , δ. We call f (c)alocal maximum value for f. The term relative

maximum, which has the same meaning as local maximum, is also used. If

f (x) # f (c) for all x in S, then we say that f has an absolute maximum at c and

that f (c) is the absolute maximum value for f. Another term for absolute

maximum is global maximum (refer to Figure 2).

DEFINITION

Let f be a function with domain S. We say that f has a local

minimum (or relative minimum) at the point c in S if there is a δ . 0 such that

f (x) $ f (c) for all x,inS such that |x 2 c| , δ. We call f (c)alocal minimum value

for f.Iff (x) $ f (c) for all x in S, then we say that f has an absolute minimum (or

global minimum)atc and that f (c) is the absolute minimum value for f (refer to

Figure 2).

The term extremum refers to either a local maximum or a local minimum. The

plural forms of “extremum,” “maximum,” and “minimum,” are “extrema,”

“maxima,” and “minima,” respectively.

If f has a local maximum at c, then f takes its greatest value at c only when

compared with nearby points. If f has a local minimum at c, then f takes its least

value at c when compared with values of f (x)

for x near c. By contrast, an absolute

maximum or minimum at c is determined by comparing f (c) with the values of f at

all points of the function’s domain. In Figure 2, f ( a )isnot the least value that the

Absolute maximum

(and a local maximum)

Absolute minimum

(and a local minimum)

Local

minimum

Local

minimum

Local

minimum

Local

maximum

Local

maximum

m Figure 2

290 Chapter

4 Applications of the Derivative

function f takes, but it is the least when compared to nearby values in the domain

of f. Therefore f has a local minimum at a but not an absolute minimum. Similarly,

f (γ) is not the greatest value that the function f takes, so f does not have an

absolute maximum at γ. How ever, f (γ) is the greatest value when compared to

nearby values. Therefore f has a local maximum at γ.

If f (c) is the greatest value of f when compared to all points of the domain,

then it is certainly the greatest value when compared to all nearby points. In other

words, an absolute maximum value is a local maximum value. The converse is not

necessarily true, as Figure 2 shows. Similarly, if an absolute minimum value occurs

at a point c, then a local minimum value also occurs at c, although the converse is

not true.

⁄ EX

AMPLE 2 Discuss local and absolute extreme values for the function

f (x) 5 sec (x), 2 3π # x # 3π.

Solution Exami

ne the graph of f in Figure 3. The function f has many local

maxima, for instance, at 23π, 2π, π,and3π. It also has many local minima, for

instance, at 22π, 0, and 2π. None of these local maxima and minima are absolute

maxima and minima, for sec (x) takes both positive and negative values that are

large in absolute value, without bound.

Locating Maxima

and Minima

We want to know how to ﬁnd the local maxima and minima of a given function.

The next theorem identiﬁes some of the points we should examine.

THEOREM 1

(Fermat) Let f be deﬁned on an open interval that contains the

point c. Suppose that f is differentiable at c.Iff has a local extreme value at c,

then f

Proof. Suppose

that f has a local maximum value at c. By deﬁnition, there is a δ . 0

such that f (x) # f (c) for all x within δ of c.IfΔx is smaller than δ, then x 5 c 1 Δx

is within δ of c and so f (c 1 Δx) 2 f (c ) # 0. When we write f

lim

Δx-0



f ðc 1 Δ x Þ2 f ðc Þ



=Δx in terms of its two one-sided limits, we obtain

ðcÞ5 lim

Δ x-0

f ðc 1 Δ x Þ2 f ðcÞ

Δx

5 lim

Δ x-0

negative numerator

positive denominator

# 0

and

ðcÞ5 lim

Δ x-0

f ðc 1 ΔxÞ2 f ð cÞ

Δx

5 lim

Δ x-0

negative numerator

negative denominator

$ 0:

Taken together, these two inequalities imply that f

to the same conclusion when f has a local minimum value at c. ’

INSIGHT

Fermat’s Theorem has a geometric interpretation: The graph of a dif-

ferentiable function has a horizontal tangent at a local extremum (as we observed in

Figure 1). Fermat’s Theorem, it should be noted, does not apply to endpoints, such as

a and b in Figure 2.

2p

m Figure 3 f (x) 5 sec (x)

4.2 The Mean Value Theorem 291

We must be careful when applying Theorem 1. Notice the direction of the

implication: If a local extreme value occurs at c, then f

entiate a function f and ﬁnd the places where f

(x) 5 0. Fermat’s Theorem says that

these are the points we should be considering to identify the local extrema of f.

However, Fermat’s Theorem does not tell us that these candidates must actually be

extrema. Figure 4 shows us some of the possibilities that can occur. Notice in par-

ticular that f

(γ) 5 0, but f does not have a local extremum at γ.Insummary,

Fermat’s Theorem cannot be used for concluding that a local extremum occurs at a

point; it can only be used to locate candidates for a local extremum.

⁄ EX

AMPLE 3 Use the ﬁrst deriv ative to locate local and absolute extrema

for the function f (x) 5 cos (x).

Solution First

note that f is differentiable on the entire real line, so Fermat’ s

Theorem applies. We calculate that f

(x) 52sin (x); therefore, f

(x) 5 0 when

x 5 ...,2 3 π, 22π, 2π,0,π,2π, . . . . Are there local maxima or local minima at

these points, or neither? First, there are local minima (indeed absolute minima)

at the points . . . , 23π, 2π, π, . . . . This is true because the value of f is 21at

these points, which is certainly the absolute minimum value for cosine because

21 # cos (x) # 1 for all x. Second, there are local maxima (indeed absolute

maxima) at the points . . . , 22π,0,2π, . . . . This is true because the value of f is 11

at these points, which is certainly an absolute maximum value for cosine. Are there

any other local maxima and minima for f ? If there were, then Fermat’s Theorem

guarantees that f

would vanish there. But we have already checked all the points

where f

vanishes, so we have found all local maxima and minima. ¥

⁄ EXAMPLE 4 Use Fermat’s Theorem to determine whether the function

f (x) 5 x

has any local or absolute extrema.

Solution Obse

rve that f is differentiable at every point. Therefore we may use

Fermat’s Theorem. We calculate that f

(x) 5 3x

.Thustheonlyzerooff

is the point

x 5 0. If f has a local extremum, then it must occur at x 5 0. A glance at the graph of f

in Figure 5 shows that there is neither a local maximum nor a local minimum at 0.

Does this contradict Fermat’s Theorem? The theorem says that if f has a local

maximum or minimum at x 5 c,thenf

there must be a local maximum or a minimum at c. Thus there is no contradiction.

Sba

f  0

Local minimum

f  0

Local minimum

Local maximum

f  0

Local maximum

f  0

Not a local extremum

m Figure 4

y  x

f(0)  0

m Figure 5

292 Chapter

4 Applications of the Derivative

INSIGHT

It is important to understand that we really did use Fermat’s Theorem in

Example 4. We used it to conclude that no value of x, except possibly x 5 0, could result

in a local extremum of f. After using Fermat’s Theorem to rule out most points, we must

then investigate the points that remain. Fermat’s Theorem says nothing about the

behavior of f at these remaining points.

Rolle’s Theorem and

the Mean Value

Theorem

In Section 4.3, we will resume our investigation of extreme values. For now we

continue to study what the derivative says about the graph of a function f.

THEOREM 2

(Rolle’s Theorem) Let f be a function that is continuous on [a, b]

and differentiable on (a, b). If f (a ) 5 f (b), then there is a number c in the open

interval (a, b) such that f

Proof. Because f is

continuous on [a , b], the Extreme Value Theorem (Section 2.3

of Chapter 2) guarantees that f has an absolute minimum and an absolute

maximum on the interval [a, b]. If one of these extre me values is assumed at a point

c inside the open interval (a, b), then Fermat’s Theorem tells us that f

(see Figure 6). Otherwise, one of these extreme values occurs at a and the other

at b. In this case, the maximum and minimum values of f are the same because

f (a) 5 f (b). We deduce that f is constant and f

interval (a, b). Either way, there is a point in the interior of the interval at which f

is zero. ’

⁄ EXAMPLE 5 A ball is thrown straight up from ground level. It returns

under

the force of gravity to ground level at some time t

. Assume only that the

motion is described by a differentiable function. Is the velocity of the ball ever 0?

Solution If h (t)

is height, then h (0) 5 h (t

) 5 0. By Rolle’s Theorem, there is a

time c between 0 an d t

when h

zero at time c. Our physical intuition reassures us on this point: The time c is the

time when the ball reaches its highest point. At that instant the ball is traveling

neither up nor down.

When interpreted geometrically, Rol le’s Theorem says that, if f is a differ-

entiable function with f (a) 5 f (b), then there is a point c between a and b at whi ch

the graph of f has a horizontal tangent line ‘ (refer to Figure 6). Notice that ‘ is

parallel to the line segment that joins the endpoints (a, f (a)) and (b, f (b)) of the

graph. The next theorem states that there is an analogous result when f (a) 6¼f (b).

THEOREM 3

(The Mean Val ue Theorem)Iff is a function that is continuous

on [a, b] and differentiable on (a, b), then there is a number c in the open

interval (a, b) such that

ðcÞ5

f ðbÞ2 f ðaÞ

b 2 a

f(c)  0

ᐉ

(b, f(b))

(a, f(a))

m Figure 6 Rolle’s Theorem

4.2 The Mean Value Theorem 293

INSIGHT

Look at Figure 7. The Mean Value Theorem says that there is a number c

between a and b for which the tangent line at (c, f (c)) is parallel to the line ‘ passing

through the points (a,f (a)) and (b, f (b)). This assertion is really Rolle’s Theorem in dis-

guise. To see this, simply rotate Figure 7 so that the line ‘ is horizontal (see Figure 8)—the

picture is essentially the same as that for Rolle’s Theorem. Informally, the Mean Value

Theorem is a “rotated” version of Rolle’s Theorem. See Exercise 82 for an analytical proof.

⁄ EXAMPLE 6 An automobile travels 120 miles in three hours. Assuming

that the position function p is continuous on the closed interval [0, 3] and differ-

entiable on the open interval (0, 3), can we conclude that at some moment in time,

the car is going precisely 40 miles per hour?

Solution Common

sense tells us that the answer must be “yes.” If the car were

always traveling at less than 40 mph, then in 3 hours it would travel less than 120

miles. Similarly, if the car were always traveling faster than 40 mph, then in 3 hours

it would go more than 120 miles. Therefore the car either travels at a constant

speed of 40 mph, in which case the answer to the question is obviously “yes,” or

there is a time when the car travels at a speed less than 40 mph and another time

when it travels at more than 40 mph. Because we expect the speed to be a

continuous function, we expect it to assume the intermediate value 40.

Let us use the Mean Value Theorem to give a short, more direct answer. We

are

given that p(3) 5 p(0) 1 120. By the Mean Value Theorem, there is a point c in

(0, 3) such that

ðcÞ5

pð3Þ2 pð0Þ

3 2 0

ð120 1 pð0ÞÞ2 pð0Þ

120

5 40;

as required.

An Application of the

Mean Value Theorem

We know that the derivative of a constant function is identically zero. The Mean

Value Theorem enables us to see that the converse is also true:

THEOREM 4

Let f be a differentiable function on an inte rval ( α, β).Iff

(x) 5 0

for each x in (α, β ), then f is a constant function.

Proof. Let a and b be

any two points in (α, β). By the Mean Value Theorem, there

is a c between a and b such that

f ðbÞ2 f ðaÞ

b 2 a

5 f

ðcÞ:

But, by hypothesis, f

the same value at any two points a, b in the interval (α, β). This is just another way

of saying that f is constant. ’

⁄ EX

AMPLE 7 In Section 2.6, we used properties of the exponential function

show that

ln ðxyÞ5 lnðxÞ1 lnðyÞ

for all positive x and y. Use Theorem 4 to derive this identity in a different way.

(c, f(c))

(b, f(b))

(a, f(a))

m Figure 8

(c, f(c))

ᐉ

(b, f(b))

(a, f(a))

f(b)  f(a)

b  a

f (c) 

m Figure 7

294 Chapter

4 Applications of the Derivative