Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Solution Fix y and consider the function f (x) 5 ln (xy) 2 ln (x) for x in (0,N).

Letting u 5 xy, we calculate

ðxÞ 5

lnðxyÞ2

ln ðxÞ

lnðuÞ2



ln ðuÞ



ðxyÞ2

 y 2

5 0:

It follows from Theorem 4 that f (x) is constant. To evaluate that constant, we may

choose any convenient value in the domain of f. Selecting the value 1, we calculate

f ð1Þ5



ln ðxyÞ2 ln ðxÞ





x51

5 ln ðyÞ2 ln ð1Þ5 ln ðyÞ2 0 5 ln ðyÞ:

Because f (x) is constant, we have f (x) 5 f (1), or ln (xy) 2 ln (x) 5 ln (y), for every

positive x. Adding ln (x) to each side of this equation yields the required identity.

We prove our next theorem now because it follows quickly from Theorem 4.

We will not use it until Section 4.9 but, beginning with that section, it will play an

important role in our studies.

THEOREM 5

If F and G are differentiable functions such that F

(x) 5 G

(x) for

every x in (α, β), then there is a constant C such that G (x) 5 F (x) 1 C for every

x in the interval (α, β).

Proof. Theorem

4 applied to the function f (x) 5 G (x) 2 F (x) tells us that there is a

constant C such that f (x) 5 C for each x in (α, β). Thus G (x) 2 F (x) 5 C,or

G (x) 5 F (x) 1 C. ’

⁄ EXAMPLE 8 Suppose that F

(x) 5 2x for all x and that F (1) 5 10. Find

F (4).

Solution If

we set G (x ) 5 x

, then G

(x) 5 2x. Thus F

(x) 5 G

(x) for every x.

According to Theorem 5, the function F that we seek must have the form

5 F (x) 1 C where C is a constant. Now we use the information F (1) 5 10 to

determine the speciﬁc value of C. Substituting x 5 1inx

5 F (x) 1 C, we obtain

5 F (1) 1 C,orF (1) 5 1 2 C. Equating our two values for F (1), we have

10 5 1 2 C,orC 529. Therefore x

5 F (x) 2 9, or F (x) 5 x

1 9. It follows that

F (4) 5 16 1 9 5 25.

4.2 The Mean Value Theorem 295

QUICK QUIZ

1. Suppose that f is differentiable on an open interval containing the point c.

a. True or false: if f

b. True or false: if a local extremum of f (x)

occurs at x 5 c, then f

2. The function f (x) 5 xe

has a local maximum. Where does it occur?

3. What upper bound on the number of local extrema of f (x) 5

1 ax

1 bx

1 cx 1 d can be deduced from Fermat’s Theorem?

4. If f is continuous on [7, 13], differentiable on (7, 13), and if f (7) 5 11 and f (13) 5 41,

then what value must f

(x)assumeforsomex in (7, 13)?

5. If F

(x) 5 2 cos (x) and F (π) 5 3, then what is F (π/6)?

Answers

1. a. false; b. true 2. 1 3. 3 4. 5 5. 4

EXERCISES

Problems for Practice

c In each of Exercises 126, a function f is given. Locate

each point c for which f (c) is a local extremum for f. (Calculus

is not needed for these exercises.) b

1. f (x) 5 (x 2 2)

1 3

2. f (x) 5 2 2 4(x 2 6)

3. f (x) 5 1/(x

1 1)

4. f (x) 5 1/((x 2 2)

1 4)

5. f (x) 5 3 sin (4x)

6. f (x) 5 exp (2|x|)

c In each of Exercises 7222, use Fermat’s Theorem to locate

each c for

which f (c) is a candidate extreme value of the given

function f. b

7. f (x) 5 2x

2 24x 1 36

8. f (x) 5 12x

1 48x

9. f (x) 5 x

2 2x

1 1

10. f (x) 5 cot (x)

11. f (x) 5 (x 2 3)(x 1 5)

12. f (x) 5 x/(x

1 1)

13. f (x) 5 x 2 ln (x)

14. f (x) 5 x 1 1/x

15. f (x) 5 e

2 x

16. f (x) 5 xe

17. f (x) 5 e

18. f (x) 5 x ln (x)

19. f (x) 5 ln (x)/x

20. f (x) 5

ﬃﬃﬃ

1 2=

ﬃﬃﬃ

21. f (x) 5 x

3/2

2 9x

1/2

22. f (x) 5 x/(1 1 x 1 x

)

c In each of Exercises 23228, verify that the hypotheses of

the

Rolle’s Theorem hold for the given function f and interval

I. The theorem asserts that f

such a c. b

23. x 1 1=x; I 5 ½1=3; 3

24. expðxÞ1 expð2xÞ; I 5 ½21; 1

25.

x 2 x

3=2

; I 5 ½0; 1

26. cos ð2xÞ1 sinðxÞ ; I 5 ½π=6; 5π=6 

27.

f ðxÞ5 x

1 4x

1 x 2 6; I 5 ½22; 1

28.

ln ðx

2 4x 1 7Þ; I 5 ½1; 3

c In each of Exercises 29234, verify that the hypotheses of

the

Mean Value Theorem hold for the given function f and

interval I. The theorem asserts that, for some c in I, the

derivative f

29. f ðxÞ5 x

1 7x

2 9x

1 x; I 5 ½0; 1

30.

f ðxÞ5 x

 sinðxÞ; I 5 ½0; π=2

31.

f ðxÞ5 x

1=5

; I 5 ½1; 32

32.

f ðxÞ52ðx 2 2Þ

1 4; I 5 ½22; 4

33.

f ðxÞ52ðx 2 1Þ

1 1; I 5 ½21; 2

34.

f ðxÞ5 x

1 2x 1 3; I 5 ½21; 4

c In each of Exercises 35240, an expression f (x)

is given.

Find all functions F such that F

(x) 5 f (x). b

35. 5

36. 3x

37. x

1 π

38. 4x

1/2

1 3

39. cos (x)

40. 3 sin (x) 2 4x

c In each of Exercises 41248, use the given information to

ﬁnd F (c). b

41.

ðxÞ5 3x

; Fð2Þ524; c 5 3

42. F

ðxÞ5 4 sinðxÞ; Fðπ=3Þ5 3; c 5 π

43.

ðxÞ5 4=x; Fðe

Þ5 7; c 5 e

44.

ðxÞ5 secðxÞ

; Fðπ=4Þ5 0; c 5 π=3

45.

ðxÞ5 e

; Fð2Þ5 2 1 e

; c 5 3

46.

ðxÞ5 2=

ﬃﬃﬃ

; Fð4Þ5 6; c 5 9

296 Chapter 4 Applications of the Derivative

47.

ðxÞ5 2=x

; Fð21Þ5 4; c 5 4

48.

ðxÞ5 2

 ln

ð2Þ; Fð1Þ5 1 1 2lnð2Þ; c 5 3

Further Theory and Practice

c In Exercises 49252 ﬁnd a value c the existence of which is

guaranteed by Rolle’s Theorem applied to the given function

f on the given interval I . b

49. f ðxÞ5 e

sinðxÞ; I 5 ½0; π

50.

f ðxÞ5 x

2 x; I 5 ½0; 1

51. f ðxÞ5 sinðxÞ1 cosðxÞ; I 5 ½2π=4; 3π=4

52.

f ðxÞ5 ðx

1 xÞ=ðx

1 1Þ; I 5 ½21; 0

c In Exercises 53256, ﬁnd a value c whose

existence is

guaranteed by the Mean Value Theorem applied to the given

function f on the interval I 5 [a, b]. b

53. f ðxÞ5 x=ðx 2 1Þ; I 5 ½2; 4

54.

f ðxÞ5 Ax

1 B ðA 6¼ 0Þ; I 5 ½a; b

55.

f ðxÞ5 x

1 3x 2 1; I 5 ½1; 7

56. f ðxÞ5 x 1 1=x; I 5 ½1; 2

c In each of Exercises 57260, a continuous function f is

given

on an interval I 5 [a, b]. Sketch the graph of y 5 f (x)

for x in I. In each case, explain why there can be no c in (a, b)

for which equation (4.2.1) holds. Explain why the Mean

Value Theorem is not contradicted. b

57. f ðxÞ5 jx 2 5j ; I 5 ½4; 7

58.

f ðxÞ5 ðx

2 2x 1 1Þ

1=4

; I 5 ½0; 2

59. f ðxÞ5 exp ð2jxjÞ; I 5 ½21; 1

60. f ðxÞ5

x 2 5if23 # x #21

2x 2 7if21 , x # 2

; I 5 ½23; 2



61. Use Theorem 4 with f (x) 5 cos

(x) 1 sin

(x) to prove the

identity cos

(x) 1 sin

(x) 5 1.

62. UseTheorem5withF (x) 5 sec

(x)andG (x)5 tan

(x)to

prove the identity 1 1 tan

(x) 5 sec

(x).

63. Show that 3x

2 4x

1 6x

2 12x 1 5 5 0 has at most two

real valued solutions.

64. Show that x

2 3x

1 4x 2 1 5 0 has exactly one real root.

65. Show that x

1 3x

1 2x 1 1 5 0 has exactly one real root.

66. Use Rolle’s Theorem to show that p (x) 5 x

1 ax

1 b

cannot have three negative roots.

67. Use Rolle’s Theorem to prove that p (x) 5 x

1 ax

1 b

cannot have two distinct negative roots if a , 0.

68. Show that p (x) 5 x

1 ax 1 b cannot have three negative

roots.

69. Use Rolle’s Theorem to prove that p (x) 5 x

ax 1 b can

have only one real root if a . 0.

70. Suppose that f (x), g(x), and h(x) are continuous for x $ a

and differentiable for x . a. Use the Mean Value

Theorem to show that if h (a) 5 0 and 0 , h

(x) for a , x,

then 0 , h (x) for a , x. Deduce that if g (a) # f (a) and g

(x) , f

(x) for a , x, then g (x) , f (x) for a , x.

71. Bernoulli’s inequality states that 1 1 px , (1 1 x)

for

0 , x and 1 , p. Use Exercise 70 to prove this.

72. Use the Mean Value Theorem to show that

(1 1 x)

, 1 1 px for 0 , x and p , 1.

73. Use the Mean Value Theorem to show that sin (x) , x for

0 , x.

74. Suppose that f satisﬁes the conditions of the Mean Value

Theorem on [a, b]. Show that if 0 , h , b 2 a, then there

exists a θ 2(0, 1) such that f (a 1 h) 5 f (a) 1 h f

(a 1 θh).

75. Suppose that p is a differentiable function such that

p (a) 5 p (b ) 5 0. Let k be any real number. Use the

function x/e

2kx

p (x) to show that there is a c between a

and b such that p

76. Deﬁne f (x) 5 sin (1/x) for x in the interval (0, 1). Use the

Mean Value Theorem to show that f

takes on all real

values.

77. Use the Mean Value Theorem to prove that

lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 1

ﬃﬃﬃ

Þ5 0:

78. Consider f (x) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

on the interval [h/2, h]. Use the

Mean Value Theorem to prove that

lim

x-0



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 h

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 h=2



79. Suppose that f : R-R is a differentiable function and that

| f

(x)| # C

for all x, where C

is a numerical constant.

Prove that



f ðsÞ2 f ðtÞ







s 2 t



for all s, t 2 R.

80. Use Theorem 4 to show that

arctan ðxÞ1 arctan ð1=xÞ5

; x . 0:

81. Use Theorem 5 to show that

2  arctan ð

ﬃﬃﬃ

Þ5 arcsin



x 2 1

x 1 1



; x $ 0:

82. Analytic Proof of the Mean Value Theorem Suppose that

f satisﬁes the hypotheses of the Mean Value Theorem.

Deﬁne g by

gðxÞ5 f ðxÞ2



f ðaÞ1

f ðbÞ2 f ðaÞ

b 2 a

ðx 2 aÞ



Apply Rolle’s Theorem to g. Deduce the assertion of the

Mean Value Theorem.

83. Suppose that f satisﬁes the hypotheses of Rolle’s Theo-

rem on [a, b]. In this exercise we will construct a sequence

f½a

; b

g

n 5 0

of intervals with the properties

(1) ½a

; b

½a

n21

; b

n21

 for n $ 1;

(2) b

2 a

5 ðb

n21

2 a

n21

Þ=2 for n $ 1;

(3) f ða

Þ5 f ðb

Þ for n $ 0; and

4.2 The Mean Value Theorem 297

(4) There exists a point c 2 (a, b) for which

c 5 lim

n-N

5 lim

n-N

and

ðcÞ5 lim

n-N

f ðb

Þ2 f ða

2 a

5 0:

If f ðða 1 b=2Þ¼f ðaÞ, then set a

5 ða 1 bÞ=2 and b

5 b.

Otherwise, set a

5 a and b

5 b. Let gðxÞ5

f ðx 1 ðb

2 a

Þ=2Þ2 f ðxÞ. Use the Intermediate Value

Theorem to ﬁnd an a

2½a

; ða

1 b

Þ=2Þ such that

gða

Þ5 0. Let b

5 a

1 ðb 2 aÞ=2. Show that

f ða

Þ5 f ðb

Þ. Replacing a

and b

with a

and b

in the

deﬁnition of g, ﬁnd a

and b

for which properties (1), (2),

and (3) hold for n 5 2. Repeat this construction indeﬁ-

nitely. Prove property (4), thereby establishing Rolle’s

Theorem.

c Discrete Dynamical Systems. Suppose that Φ : R - R is

continuous function. The collection of sequences {x

}

n $ 0

that

satisﬁes x

n11

5 Φ(x

) for n $ 0 is called the discrete dynamical

system associated with Φ. Notice that each element {x

}ofa

discrete dynamical system is determined by its ﬁrst element

. A number x

such that Φ(x

) 5 x

is called an equilibrium

point of the dynamical system. We say that an equilibrium

point x

of Φ is stable if there is a δ . 0 such that each element

} of the dynamical system associated to Φ converges to x

provided that |x

2 x

| , δ. Exercises 84289 are concerned

with these ideas. b

84. Suppose

that x

is an equilibrium point of the dynamical

system. Show that if x

5 x

, then x

5 x

for all n $ N.

If x

5 x

, then x

N11

5 Φ (x

) 5 Φ (x

) 5 x

. Continuing,

N12

5 Φ (x

N11

) 5 Φ (x

) 5 x

, and so on. (In words, once

a member of the sequence {x

} equals x

, its successor

equals x

as well.) It follows that once a member of the

sequence {x

} equals x

, all subsequent members equal x

85. Suppose that {x

}

n $ 0

is an element of the discrete dyna-

mical system associated with Φ. Suppose that

ξ 5 lim

n-N

: Show that ξ is an equilibrium point of the

discrete dynamical system associated with Φ.

86. Suppose that x

is an equilibrium point of the dynamical

system Φ. Suppose that Φ

exists and is continuous on an

open interval centered at x

. Suppose also that |Φ

)| , 1.

Show that there are positive numbers δ and K with K , 1

such that

jΦ

ðxÞj, K for every x in ðx

2δ; x

1δÞ:

Illustrate this with a sketch.

87. Continuation: Suppose that x

is in the interval (x

2 δ,

1 δ). Deduce that x

5 Φ(x

) is also in this interval by

observing that

2 x

j5 jΦðx

Þ2 Φðx

Þj# Kjx

2 x

Explain the reasoning behind this. Illustrate the position

of x

, x

, and x

with a sketch.

88. Continuation: Follow the steps of the preceding exercise

to deduce that

2 x

j# K

2 x

89. Continuation: Prove the following theorem: If x

is an

equilibrium point of the dynamical system Φ such that (1)

exists and is continuous on an open interval centered at

and (2) | Φ

)| , 1, then x

is a stable equilibrium of Φ.

90. Let a be a positive constant and set

TðxÞ5 a  sech





ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

The curve y 5 T ( x) is known as a tractrix. Use Theorem 5

to show that if y satisﬁes the two equations

yðxÞ52

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

; yðaÞ5 0;

then y (x) 5 T (x).

Calculator/Computer Exercises

c In each of Exercises 91294, calculate and plot the deri-

vative f

of the given function f. Use this plot to identify

candidates for the local extrema of f. Add the plot of f to the

window containing the graph of f

. From this second plot,

determine the behavior of f at each candidate for a local

extremum. b

91. f (x) 5 x

2 2x 1 cos (x)

92. f (x) 5 x

2 2x ln (1 1 x

) 1 x 2 4

93. f (x) 5 x 2 2 exp (2x

)

94. f (x) 5 sin

(x) 2 x

1 5x 1 20

c In Exercises 95298,

approximate the value c guaranteed

by the application of the Mean Value Theorem to the given

function f on the given interval I 5 [a, b]. Graph the function,

the tangent line at (c, f (c )), and the line segment between

(a, f (a)) and (b, f (b)). b

95.

f ðxÞ5 x

1 x

1 1; I 5 ½0; 2

96. f ðxÞ5 xe

; I 5 ½23=2; 1

97.

f ðxÞ5 x

2 2x

1 x

2 2x 1 13; I 5 ½21; 3

98. f ðxÞ5 x sinð1=xÞ; I 5 ½1=ð4πÞ; π=24

298 Chapter 4 Applications of the Derivative

4.3 Maxima and Minima of Functions

In Section 4.2, we learned that the derivative is a useful tool for ﬁnding candidates

for local extre ma. However, we did not learn much about identifying these

extrema—the subject of this section. We begin with a consideration of what the

derivative tells us about the graph of a function. Recall the following deﬁnition

from Section 2.6 in Chapter 2:

DEFINITION

A function f is increasing on an interval I if f (s) , f (t) whenever

s and t are points in I with s , t (see Figure 1). We say that f is decreasing if

f (s) . f (t) whenever s , t (see Figure 2).

⁄ EX

AMPLE 1 Where is the function f (x ) 5 sin (x ) increasing or decreasing

on the interval (0, 2π)?

Solution As

Figure 3 shows, the function f is increasing on the intervals (0, π/2)

and (3π/2, 2π). It is decreasing on the interval (π/2, 3π/2).

The statements in Example 1 about the sine function are obvious because it is a

familiar function. What we need is a technique for telling where any differentiable

function is increasing or decreasing.

Using the Derivative to

Tell When a Function Is

Increasing or

Decreasing

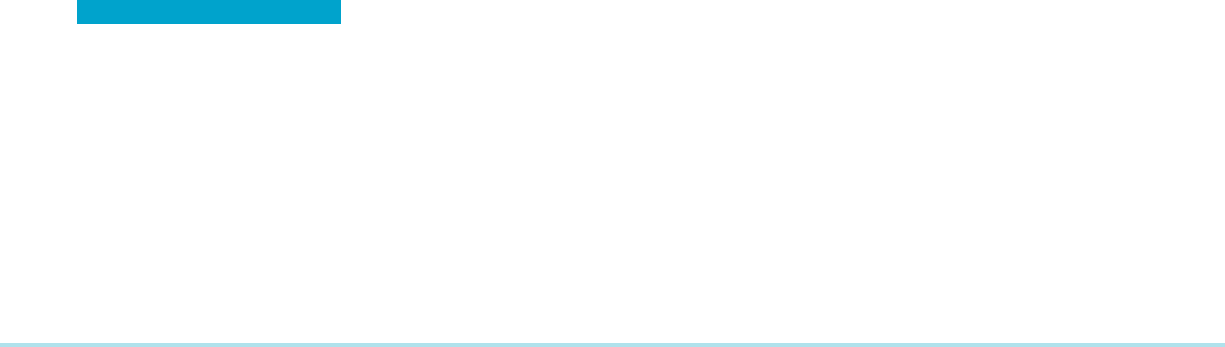
Geometric intuition suggests that rising tangent lines to the graph of y 5 f (x) occur

only where f is increasing (see Figure 4). Because the tangent line at (c, f (c)) rises if

and only if its slope is positive, which is to say f

as a tool for locating intervals on which f increases. Similarly, falling tangent lines

occur only where f is decreasing. The condition for a tangent line at (c, f (c)) to fall

is that its slope f

tionship between the sign of f

and the behavior of f precise.

THEOREM 1

If f

(x) . 0 for each x in an interval I, then f is incr easing on I.If

(x) , 0 for each x in I, then f is decreasing on I.

f(s)  f(t)

stI

f(t)

f(s)

m Figure 2 f is decreasing on I.

1

f (x)  sin(x)

p 3p

m Figure 3

m Figure 4

f(s)

f(s)  f (t)

stI

f(t)

m Figure 1 f is increasing on I.

4.3 Maxima and Minima of Functions 299

Proof. Let s , t be points in I with s , t. By the Mean Value Theorem applied to f

on the interval [s, t], there is a number c between s and t such that

f ðtÞ2 f ðsÞ

t 2 s

5 f

ðcÞ:

But, by hypothesis, f

f ðtÞ2 f ðsÞ5 f

ðcÞ

|ﬄ{zﬄ}

positive

ðt  sÞ

|ﬄﬄﬄ{zﬄﬄﬄ}

positive

> 0

or f (t) . f (s). Therefore f is increasing on I. The other statement may be proved

similarly. ’

⁄ EX

AMPLE 2 Examine the function f (x) 5 x

2 6x

1 13x 2 7 to determine

intervals on which it is increasing or decreasing.

Solution The

graph of f in Figure 6 suggests that f is increasing on the interval

[21, 5] over which it is plotted. However, the plot of f over a ﬁnite interval cannot

exhibit the behavior of f over the entire real line. Instead, we appeal to Theorem 1.

By completing the square, we see that the derivative of f is

given by

ðxÞ5

ðx

2 6x

1 13x 2 7Þ

5 3x

2 12x 1 13 5 3ðx

2 4xÞ1 13

5 3ðx

2 4x 1 4Þ2 3 ð4Þ1 13 5 3ðx 2 2Þ

1 1:

Because (x 2 2)

$ 0, we see that f

(x) . 0 for all x in R. By Theorem 1, we con-

clude that f is increasing on all of R.

It is sometimes helpful to notice that if a , b, then the two factors of

(x 2 a)(x 2 b) have the same sign if and only if x , a, in which case the factors

(x 2 a) and (x 2 b) are both negative, or x . b, in which case the factors are both

positive. We therefore see that

ðx 2 aÞðx 2 bÞ

. 0ifx , a

, 0ifa , x , b

. 0ifb , x:

⁄ EX

AMPLE 3 On which intervals is the function f (x) 5 x

2 3x

2 9x 1 5

increasing? On whi ch intervals is it decreas ing?

Solution Begin

by calculating

ðxÞ5 3x

2 6x 2 9 5 3ðx 1 1Þðx 2 3Þ5 3



x 2 ð21Þ



ðx 2 3Þ:

Using the reasoning that precedes this example, we concl ude that f

is positive on

(2N, 21) and on (3,N), and f

is negative on (21, 3) . Therefore f is increasing on

the intervals (2N, 21) and (3,N) and decreasing on the interval (21, 3). Figure 7

exhibits the graph, which includes 1 signs to indicate where f

is positive

and 2 signs to indicate where f

is negative. ¥

m Figure 5

f (x)  x

 6x

 13x  7

m Figure 6

50



1

y  x

 3x

 9x  5

m Figure 7

300 Chapter

4 Applications of the Derivative

Critical Points and the

First Derivative Test for

Local Extrema

Now that we have learned to identify where a differentiable function f is increasing or

decreasing, we can apply our knowledge to determine where f has a local maximum or

minimum. We can even apply Theorem 1 to a continuous function that is not dif-

ferentiable everywhere. This observation is important because many of the functions

that we encounter in practice are not differentiable at every point of their domains.

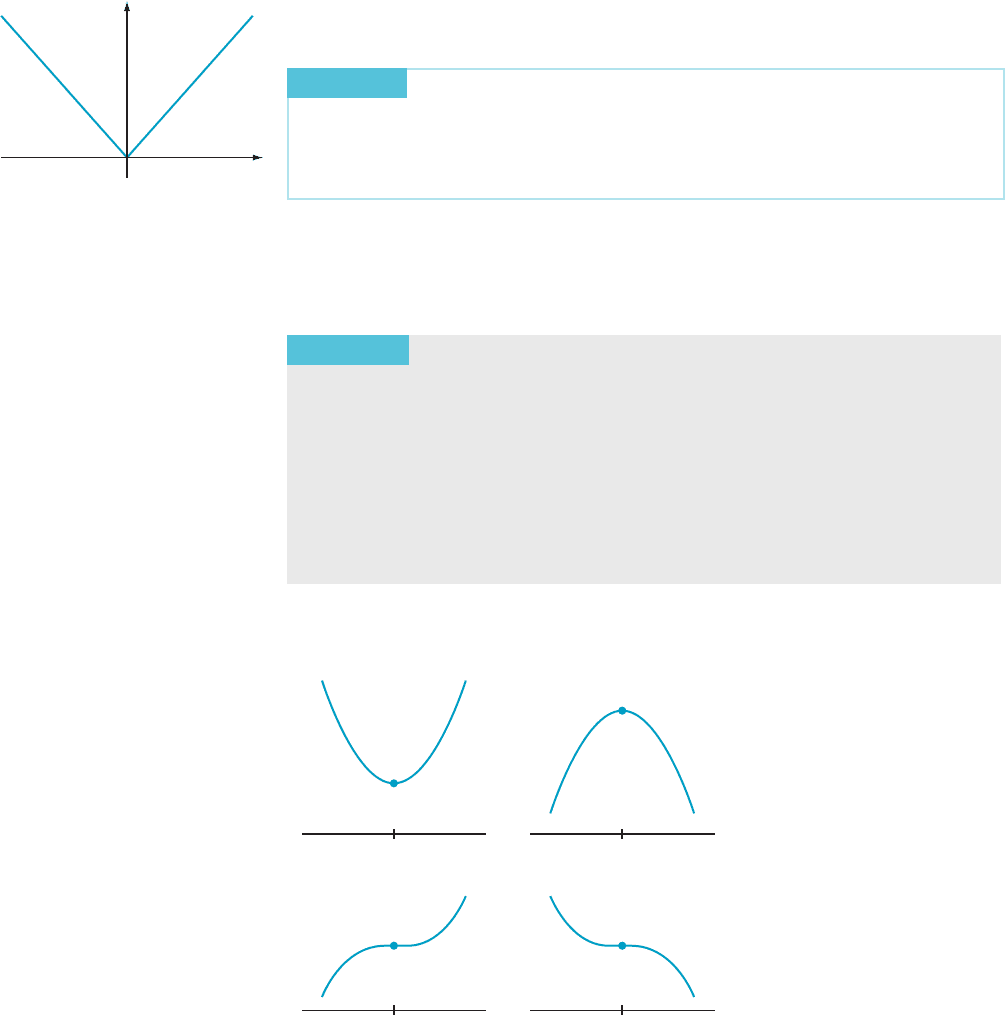
For example, the function f (x) 5 |x| is not differentiable at x 5 0, but, as we see in

Figure 8, it has an absolute minimum there. Our tests for local extrema must therefore

take into account isolated points of nondifferentiability. We begin with a deﬁnition.

DEFINITION

Let c be a point in an open interval on which f is contin uous. We

call c a critical point for f if one of the following two conditions holds:

a. f is not differentiable at c;or

b. f is differentiable at c and f

Fermat’s Theorem implies that, if the domain of a function f is an open

interval, then the critical points for f are the only places that have to be examined in

the search for the local extrema of f. The next theorem provides criteria for

determining the behavior of a function at a critical point.

THEOREM 2

(The First Derivative Test) Suppose that I 5 (α, β) is an open

interval contai ned in the domain of a continuous function f, that a point c in I is

a critical point for f, and that f is differentiable at every point of I other than c.

a. If f

(x) , 0forα , x , c and f

(x) . 0forc , x , β,thenf has a local minimum

at c.

b. If f

(x) . 0forα , x , c and f

(x) , 0forc , x , β,thenf has a local maximum

at c.

c. If f

(x) has the same sign on both sides of c , then f has neither a local

minimum nor a local maximum (even if f

The rationale for the test is obvious. Look at Figure 9. The hypotheses of part a

of the First Derivative Test imply that f is decreasing just to the left of c and

f (x)  x

m Figure 8

Decreasing

Increasing

Local

minimum

Increasing

No local

extremum

Decreasing

No local

extremum

DecreasingIncreasing

Local

maximum

m Figure 9

4.3 Maxima and Minima of Functions 301

increasing just to the right of c. It is evident that a continuous function must have a

local minimum at such a point. The hypotheses of part b of the First Derivative

Test imply that f is increasing just to the left of c and decreasing just to the right

of c. A continuous function must have a local maximum at such a point. Finally, the

hypothesis of part c implies that either f is increasing both to the left and to the

right of c,orf is decreasing both to the left and to the right of c. A continuous

function cannot have a local extremum at such a point.

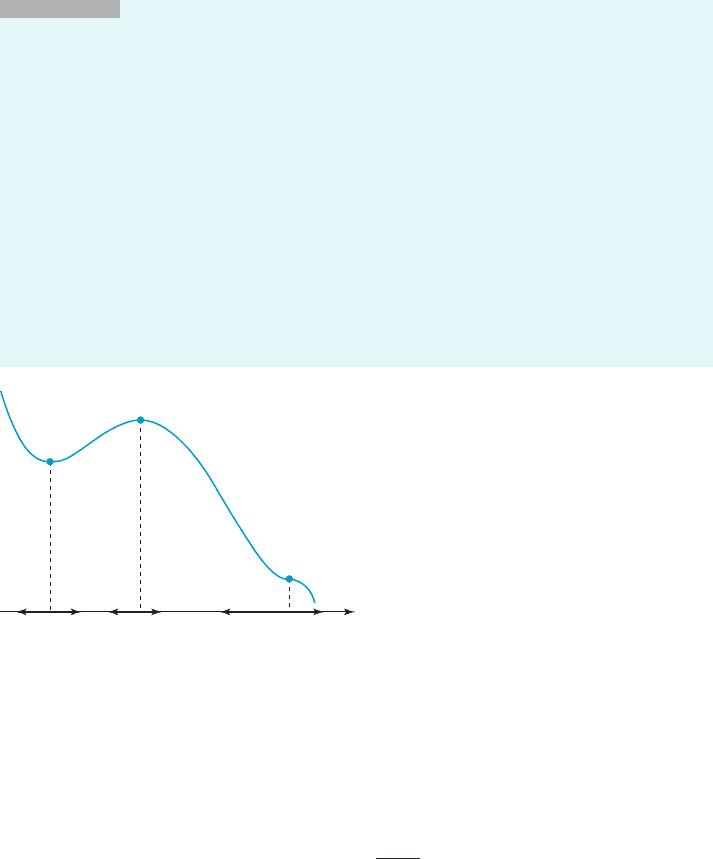
INSIGHT

When the First Derivative Test is applied, the interval I will usually be

only a part of the domain of the function, as shown in Figure 10. The length of I is

unimportant, but it must extend to each side of the critical point. As x approaches the

critical point c

from the left in Figure 10, the values f (x) decrease and so f

(x) , 0. As x

passes through and moves to the right from c

, the values f (x) increase and so f

(x) . 0.

A similar analysis at the critical point c

in Figure 10 leads us to these restatements, in

plain English, of parts (a) and (b) of the First Derivative Text:

If f

(x) changes from negative to positive as x passes through a critical point from

left to right, then f has a local minimum at the critical point.

If f

(x) changes from positive to negative as x passes through a critical point from

left to right, then f has a local maximum at the critical point.

Notice that f

(x) , 0 on both sides of critical point c

. Because the sign of the f

(x) does

not change as x passes through this critical point, part (c) of the First Derivative Test tells

us that there is no local extremum at this critical point.

⁄ EXAMPLE 4 Suppose that a river’s current has speed u and that a ﬁsh is

swimming upstream with speed v relative to the water. This implies that v . u. (If v

were equal to u, then the ﬁsh woul d be at a standstill relative to land. If v were less

than u, then the ﬁsh would be carried downstream by the current.) The energy E

expended in such a migration is

EðvÞ5 α

v 2 u

where α is a positive constant. For what value of v is E minimized?

Solution The

domain of E is the open interval (u,N). Also, E is differentiable at

all points in its domain. By Fermat’s Theorem, any local extremum will occur at a

zero of E

. Using the Quotient Rule, we calculate

y  f(x)

m Figure 10

302 Chapter

4 Applications of the Derivative

ðvÞ5 α

ðv 2 uÞ3v

2 v

ð1 2 0Þ

ðv2uÞ

5 α

2 3uv

ðv2uÞ

5 2αv

v 2 3u=2

ðv2uÞ

Setting E

(v) 5 0 yields v 5 3u/2. Notice that the sign of E

(v) is the same as the

sign of v 2 3u/2. Thus E

(v) , 0 for v , 3u/2 and E

(v) . 0 for v . 3u/2. According

to the First Derivative Test, E (v) has a local minimum at v 5 3u/2. The graphs of E

and E

in Figure 11 bear this out. ¥

⁄ EXAMPLE 5 Find and analyze the critical points for the function f (x) 5

x 2 sin (x).

Solution Becau

se f (x) is differentiable at every x, the critical points of f are the

zeros of f

. Because f

(x) 5 1 2 cos (x), we see that the zeros of f

are the numbers x

for which cos (x) 5 1. Thus the critical points are the numbers . . . , 2 4π, 22π ,0,2π,

4π, . . . . At every other point, we have cos (x) , 1 and f

(x) 5 1 2 cos (x) . 0.

Therefore f

(x) does not change sign at any critical point. Part (c) of the First

Derivative Test tells us that none of the critical points is a local extremum. The

graph of f, shown in Figure 12, conﬁrms this conclusion. Because f

is never

negative, the graph of f increases from left to right.

⁄ EXAMPLE 6 Find and analyze the critical points for the function f (x) 5 x 

(x 2 1)

1/3

Solution As

long as x 6¼1, we have

ðxÞ5 1 ðx 2 1Þ

1=3

1 x 



ðx 2 1Þ

22=3



ðx 2 1Þ1 x=3

ðx 2 1Þ

2=3

ð4=3Þx 2 1

ðx 2 1Þ

2=3

Thus f

can vanish only when the numerator 4x/3 2 1 of this fraction vanishes, or

when x 5 3/4. The function f therefore has two critical points: c 5 3/4, where f

5 0,

and c 5 1, where f is not differentiable. Notice that the denominator of the

expression for f

is always positive when x 6¼1 (because the exponent has an even

numerator). Refer to Figure 13 as you work through the analysis.

Begin with the critical point 3/4. When x is slightly to the left of 3/4, the

numerator of f

(x) is negative so f

(x) , 0. When x is slightly to the right of 3/4, the

numerator of f

(x) is positive, so f

(x) . 0. By the First Derivative Test, there is a

local minimum at c 5 3/4.

Next, consider the critical point c 5 1. When x is slightly to the left of 1, the

numerator of f

(x) is positive. The same is true when x is slightly to the right of 1.

By the First Derivative Test, c 5 1 is not a local extremum.

In later sections, we will learn how to use the second derivative to identify local

maxima and minima. We will also learn how to locate absolute maxima and

minima.

E(v)

E(v)  a

v  u

m Figure 11

(υ) , 0 for υ , 3u/2 and

(υ) . 0 for υ . 3u/2

4p2p

4p 2p

f (x)  x  sin(x)

m Figure 12

f (x)  x(x  1)

13

m Figure 13

4.3 Maxima and Minima of Functions 303

QUICK QUIZ

1. True or false: If f (x) is differentiable for every x in R and if f

either a local minimum or a local maximum when x 5 c.

2. True or false: If f (x) is differentiable for every x in R,iff

(x) . 0 for all x , c,

and if f

(x) . 0 for all x . c, then f (x) has a local minimum at x 5 c.

3. True or false: If f (x) is deﬁned for every x in R,iff

(x) . 0 for all x , c,andif

(x) , 0 for all x . c, then f (x) has a local maximum at x 5 c.

4. Find and analyze the local extrema for the function f ( x ) 5 x

/3 1 x

2 15x 1 5.

Answers

1. False 2. False 3. True 4. Local maximum at x 525;

local minimum at

x 5 3.

EXERCISES

Problems for Practice

c In each of Exercises 1228, use the ﬁrst derivative to deter-

mine the intervals on which the given function f is increasing and

on which f is decreasing. At each point c with f

First Derivative Test to determine whether f (c)isalocalmax-

imum value, a local minimum value, or neither. b

1. f ðxÞ5 x

1 x

2. f ðxÞ5 3x

1 x

1 4

3. f ðxÞ5 x

1 3x

2 45x 1 2

4. f ðxÞ5 4x

2 6x

1 8

5. f ðxÞ5 3x

1 20x

1 36x

6. f ðxÞ5 x

2 5x

7. f ðxÞ52x=ðx

1 25Þ

8. f ðxÞ5 x=ðx 1 1Þ

9. f ðxÞ5 ðx 1 1Þ=ðx 2 1Þ

10. f ðxÞ5 xðx 1 2Þ

11. f ðxÞ5 ðx 1 1Þðx 1 2Þ

12. f ðxÞ5 ðx 1 1Þ

ðx 1 2Þ

13. f ðxÞ5 ðx

2 3Þ=ðx 1 2Þ

14. f ðxÞ5 1=ðx

1 6Þ

15. f ðxÞ5 4x 1 9=x

16. f ðxÞ5 x 2

ﬃﬃﬃ

17. f ðxÞ5 3x 1 2 sinðxÞ

18. f ðxÞ5 2 cos

ðxÞ1 3x

19. f ðxÞ5 e

2 x

20. f ðxÞ5 xe

21. f ðxÞ5 x

22. f ðxÞ5 expðxÞ=x

23. f ðxÞ5 2

2 x

24. f ðxÞ5 2

2 4

25. f ðxÞ5 xlog

ðxÞ

26. f ðxÞ5 x

lnðxÞ

27. f ðxÞ5 x=lnðxÞ

28. f ðxÞ5 lnðxÞ=x

c In Exercises 29240,

ﬁnd each critical point c of the given

function f. Then use the First Derivative Test to determine

whether f (c) is a local maximum value, a local minimum

value, or neither. b

29. f ðxÞ5 xðx 1 1Þ

3=2

; 21 , x

30. f ðxÞ5 x

1=3

ðx 1 2Þ

3=2

; 22 , x

31. f ðxÞ5 x

1=5

ðx 2 12Þ

32. f ðxÞ5 x

2=3

ðx 1 10Þ

33. f ðxÞ5 3x 2 x

1=3

34. f ðxÞ5 x

3=2

2 6x

1=2

; 0 , x

35. f ðxÞ5 x

2=3

2 4x

1=3

36. f ðxÞ5 3x

1=3

2 5x

1=5

37. f ðxÞ5 ðx 2 1Þ

1=3

ðx 1 5Þ

2=3

38. f ðxÞ5 ðx 1 1Þ

2=3

39. f ðxÞ5 ðx 2 4Þ

1=5

ð3x 1 1Þ

2=3

40. f ðxÞ5 jx 1 1j=ðx

1 15Þ

41. A function f

has been plotted in Figure 14. Determine on

what intervals f is increasing and on what intervals f is

decreasing.

42. A derivative f

has been plotted in Figure 15. Determine

the points where f (x) changes (as x moves to the right)

from being increasing to being decreasing. Determine the

f 

1.0

1.0

2.0

1.0

m Figure 14

304 Chapter

4 Applications of the Derivative