Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

points where f changes from being decreasing to being

increasing.

Further Theory and Practice

c Find and test the critical points of the functions in Exer-

cises 43247: b

43. f ðxÞ5 2x

2 2x

44. f ðxÞ5 jx 2 7j1 x

45. f ðxÞ5 5x 2 j8 2 3xj

46. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

j2x 1 9j

47. f ðxÞ5 x

1=3

2 jxj

c In each of Exercises 48253,afunctionf is

given. In each

case, the domain of f and the value of f (x) depend on a positive

constant b. Determine each point at which f has a local extre-

mum. Use the First Derivative Test to classify the extremum. b

48. f ðxÞ5 x 1 4b

=x; b , x

49. f ðxÞ5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

; 0 , x , b

50. f ðxÞ5 x

=ð3x 2 bÞ; b=3 , x

51. f ðxÞ5 ðx

1 3b

Þ=ðb 2 xÞ; x , b

52. f ðxÞ5 ðx 1 bÞ=ðx

1 15b

Þ; 2 b , x

53. f ðxÞ5 ðx

1 8b

Þ=ðx

1 b

Þ; b , x

c In each of Exercises 54260, determine each point c,

where

the given function f satisﬁes f

the First Derivative Test to determine whether f has a local

maximum, a local minimum, or neither. b

54. f ðxÞ5 arctanðxÞ2 x=5

55. f ðxÞ5 arcsinðxÞ2

ﬃﬃ

ﬃ

56. f ðxÞ5 2 arctan ðxÞ2 arcsinðxÞ

57. f ðxÞ5 sinhðxÞ1 2 cosh ðxÞ

58. f ðxÞ5 tanhðxÞ2 expð2xÞ

59. f ðxÞ5 2 sinh

ðxÞ2 ln ðxÞ

60. f ðxÞ5 tanh

ﬃﬃﬃ

Þ2 2

ﬃﬃﬃ

61. Let f be differentiable on, R. Suppose that f

(2) . 0. Is

f (2.000001) . f (2)? Explain your answer.

62. True or false:Iff : R-R is a polynomial and if f has two

local minima, then it has a local maximum. Explain your

answer.

63. Prove that if f: R-R is differentiable, and f

. 0 every-

where, then f is one-to-one. Prove that if f

, 0

everywhere, then f is one-to-one.

64. If f is increasing on an interval I, does it follow that f

increasing? What if the range of f is (0,N)?

65. Prove that if a differentiable function f is increasing on an

interval I, then f

is increasing.

66. Suppose that a real-valued function f is deﬁned and

increasing on an interval (a, b). Let J be the image of f.

Without using calculus, prove that f

: J - (a, b) exists

and is increasing. Now assume that f

exists and is positive

on the interval (a, b). Give a calculus proof that f

increasing.

67. Without using calculus, prove that the composition of two

increasing functions is increasing. Now assume that f and

g are differentiable functions with positive derivatives and

that g 3 f is deﬁned. Use calculus to show that g 3 f is

increasing.

68. Assume that f and g are decreasing, differentiable func-

tions and that g 3 f is deﬁned. Use calculus to show that

g 3 f is increasing.

69. Let f (x) 5 ax

1 bx 1 c with a 6¼0. By completing the

square, determine the interval(s) on which f is increasing

and the interval(s) on which f is decreasing. Use the

derivative of f to verify your conclusions.

70. The reaction rate V of a common enzyme reaction is

given in terms of substrate level s and the Michaelis

constant K by,

V 5

K 1 S

ðS $ 0Þ:

Show that V is an increasing function of S. It follows that

V has no absolute maximum value. Is V bounded? What

is lim

S-N

71. Suppose that f (x) 5 (x 2 a)(x 2 b) q (x) where q is a

polynomial that is positive on an interval (α, β) containing

[a, b]. Show that f

(a) f

(b) , 0.

72. The function f

has been plotted in Figure 16. It is known

that f

(A) 5 0, f

(B) 5 0, f

(D) 5 0. Deter-

mine whether f has any local extreme values at the points

A, B, C, and D. Explain your reasoning.

73. In economic theory, the product of labor f (n) measures

commodity output as a function of the level n of labor

BC D E F HGI

f

m Figure 15

f 

m Figure 16

4.3 Maxima and Minima of Functions 305

input. The marginal product of labor (MPL) represents

the extra output that results from one additional unit of

work. In general, the function MPL has a certain property

that is illustrated in three different ways by the graphs in

Figure 17. What is the property? Explain how the graphs

illustrate it.

74. Give necessary and sufﬁcient algebraic conditions on the

coefﬁcients of the polynomial

pðxÞ5 ax

1 bx

1 cx 1 d

that guarantee that p is increasing on the entire real line.

75. Let f : R- (0,N) be a differentiable function. Compare

the local extrema of f with those for 1/f. The local maxima

for f become what for 1/f ? The local minima for f become

what for 1/f ?

76. Suppose that f (c) and g (c) are positive. The Product and

Quotient Rules state

ðf  gÞ

ðcÞ5

1 f

ðcÞgðcÞ1 f ðcÞg

ðcÞ

and



ðcÞ5

1 gðc Þf

ðcÞ2 g

ðcÞf ðcÞ;

gðcÞ

respectively. The unusual presentation here serves to

highlight some similarities between the two rules. Notice

that both ( f g)

denominator. Also notice that each of the terms f

g (c) and f (c) g

you learned about the derivative in this section, explain

why each of the four signs makes sense.

77. If T is the temperature in degrees Kelvin of a white dwarf

star, then the rate at which T changes as a function of time

t is given by dT/dt 52αT

7/2

where α is a positive constant.

Do white dwarfs cool or heat up? Is the rate at which a

white dwarf’s temperature changes increasing or

decreasing? Explain your answers.

78. According to Saha’s equation, the fraction x A (0, 1) of

ionized hydrogen atoms in a stellar mass depends on

temperature T according to the equation

1 2 x

5 A  T

23=2

 exp





for positive constants A and K.

a. Without differentiating, explain why the right side of

this equation is a decreasing function of T.

b. Without differentiating, explain why the left side of

this equation is a decreasing function of x.

c. Without differentiating, explain why x is an increasing

function of T.

d. Use part c to explain why Saha’s equation determines

x as a function of T.

e. By differentiating implicitly, verify that x is an

increasing function of T.

79. Show that the function y / y exp (y) is increasing for

y . 0. Deduce that for every positive x, there is a unique y

such that y exp (y) 5 x. This relationship inplicitly deter-

mines a function that is often denoted by W and is called

Lambert’s W function:

WðxÞexp



WðxÞ



5 x ðx . 0Þ:

Use implicit differentiation to show that W is an

increasing function. Show that

ðxÞ5

WðxÞ



1 1 WðxÞ



80. In this exercise, you will show that

lim

n-N

1=n

5 1

following a proof of Alan Beardon. Suppose that

0 , p , 1. Deﬁne f (x) 5 px 2 x

for # x ,N. By calculat-

ing f

(x), show that f (1) # f(x). Use this inequality to

deduce that x

# px 1 1 2 p. In this inequality, set x 5

ﬃﬃﬃ

and p 5 1/n, and use the Pinching Theorem to show that

lim

n-N

1=n

5 1:

81. Darboux’s Theorem (after Jean Darboux, 18421917)

states that if f

exists at every point of an open interval

y

 y



. . .

y

MPL

m Figure 17

306 Chapter

4 Applications of the Derivative

containing [a, b], and if γ is between f

(a) and f

(b), then

there is a c in the interval (a, b) such that f

existence of such a c follows from the Intermediate Value

Theorem if f

is assumed continuous. Darboux’s Theo-

rem, which you will prove in this exercise, tells us that the

assumption of continuity is not needed for functions that

are derivatives. Suppose for deﬁniteness that f

(a) , γ ,

(b). Deﬁne g on [a, b]byg (x) 5 f (x) 2 γ x.

a. Explain why g has a minimum value that occurs at

some point c in (a, b).

b. Show that f

c. Use Darboux’s Theorem to show that if f increases on

the interval (l, c) and decreases on the interval (c, r) (or

vice versa), then f

Calculator/Computer Exercises

c In each of Exercises 82289, use the ﬁrst derivative to

determine the intervals on which the function is increasing

and on which the function is decreasing. b

82. f ðxÞ5 x

2 x

2 7:1x 1 3:2

83. f ðxÞ5 x

2 4x

1 3:94x

2 3:87x

84. f ðxÞ5 2x

2 1:2x

2 13:7x 1 5:2

85. f ðxÞ5

x 1 e

1 e

86. f ðxÞ5 ðx

1 x 1 1Þ=ðx

1 1Þ

87. f ðxÞ5 x

2 x

1 e

88. f ðxÞ5 ð4x

2 3Þexpð2x

89. f ðxÞ5 x

1=3

2 lnð1 1 x

c In each of Exercises 90293, a function f is

given. Calculate

and plot y 5 f

(x) in a suitable viewing window. Use this

plot to identify the points at which f has local extrema. b

90. f ðxÞ5 x

2 x 1 sin

ðπx=2Þ; 21 , x , 1

91. f ðxÞ5 2 1 x

=3 2 sin

ðx 1 1Þ; 23 , x , 3

92. f ðxÞ5 lnðxÞlnð1 2 x

93. f ðxÞ5 expð2x

Þ1 exp



2ðx 2 1Þ



1 exp



2ðx 2 3Þ



;

22 , x , 5

94. For each given function f, graph the function S (x) 5

signum( f

(x)) for x in the given interval I . Use the graph

of S to determine and classify the local extrema of f.

a. f (x) 5 x

2 12x

1 55x

2 120x

1 124x 2 48,

I 5 [0.8, 4.1]

b. f (x) 5 4x

2 24x

1 51x

2 44x 1 12, I 5 [0.3, 2.6]

c. f (x) 5 x

2 x

2 7x

1 x 1 6, I 5 [22.4, 3.2]

4.4 Applied Maximum-Minimum Problems

In this section, we learn how to apply the techniques of calculus to study a variety

of practical problems, all of which involve ﬁnding the maximum or minimum of

some quantity. Therefore we will certainly make use of the ideas that were intro-

duced in Section 4.3. In this section, however, we concentrate on ﬁnding absolute

extrema. Our ﬁrst example illustrates the important role that endpoints play in such

a search.

⁄ EX

AMPLE 1 The total mechanical power P (in watts) that an individual

requires for walking a ﬁxed distance at constant speed v (in kilometers per hour)

with step length s (in meters) is

PðsÞ5 α

1 βvs



0 , s # L



;

where L is the individual’s maximum step size. In this example, we use L 5 1 m.

The positive constants α and β depend on the distance walked and the individual’s

gait. In this example, we use α 5 1.4 and β 5 45. For what s is P(s) minimized if

v 5 5? If v 5 6?

Solution We

calculate that

ðsÞ5



1 βvs



52α

1 βv 5

βv





βv

ðs 1 s

Þðs 2 s

Þ;

4.4 Applied Maximum-Minimum Problems 307

where s

5 v

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

α=β:

From this formu la, we see that s 5 s

is the unique positive

solution of the equation P

(s) 5 0. For v 5 5, we have s

5 v

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

α=β

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1:4=45

 0:88; which is less than L and therefore in the domain of P. For

0 , s , s

, we have

ðsÞ5

βv

ðs 1 s

|ﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄ}

positive

ðs 2 s

|ﬄﬄﬄﬄ{zﬄﬄﬄﬄ}

negative

, 0;

and for s

, s # L, we have

ðsÞ5

βv

ðs 1 s

|ﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄ}

positive

ðs 2 s

|ﬄﬄﬄﬄ{zﬄﬄﬄﬄ}

positive

. 0:

We conclude that P decreases on the interval (0, s

) and increases on the interval

, L]. Therefore P has an absolute minimum at s 5 s

. The graph of P conﬁrms our

analysis (see Figure 1).

For v 5 6, the value of s

5 v

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

α=β

5 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1:4=45

is about 1.06, which is greater

than L and, therefore outside the domain of P. Of course, P cannot have a mini-

mum at a point that is not in its domain. To determine the point at which P (s)is

minimized, observe that, for all 0 , s # L,

ðsÞ5

βv

ðs 1 s

|ﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄ}

positive

ðs 2 s

Þ,

βv

ðs 1 s

|ﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄ}

positive

ðL 2 s

|ﬄﬄﬄﬄ{zﬄﬄﬄﬄ}

negative

, 0:

We conclude that P is decreasing on its entire domain (0, L]. Therefore P (s)is

minimized when s 5 L (see Figure 2).

INSIGHT

Example 1 shows us that when we determine the absolute extrema of a

function, we must consider its domain. If a function is deﬁned at an endpoint of its

domain, then an extreme value of the function may occur there.

Closed Intervals Let us consider the absolute extrema of a continuous function f on a closed interval

[a, b]. The Extreme Value Theorem (Section 2.3 of Chapter 2) guarantees that f has

both an absolute maximum and an absolute minimum in [a, b]. Also, the techniques

of Section 4.3 guarantee that if these extrema are inside the open interval (a, b),

then they will be found among the critical points. It is possible, however, that the

absolute maximum or absolute minimum of f could be at a or at b. We therefore

rely on the following procedure.

Basic Rule for Finding Extrema of a Continuo us Function on a Closed Bounded Interval

To ﬁnd the extrema of a continuous function f on a closed interval [a, b], we test

a. The points in (a, b) where f is not differentiable;

b. The points in (a, b) where f

exists and equals 0;

c. The endpoints a and b.

In brief, we should test the critical point s and the endpoints.

 0.88

P(s)  a  bvs

m Figure 1

P(s)  a  bvs

m Figure 2

308 Chapter

4 Applications of the Derivative

⁄ EXAMPLE 2 A man builds a rectangular garden along the side of his

house. He will put fencing on three sides (see Figure 3). If he has 200 feet of fencing

available, then what dimensions will yield the garden of greatest area?

Solution The

function that we must maximize is A, the area inside the fence. If ‘

denotes length, and w denotes width, as in Figure 3, then A 5 ‘ w. The trouble is

that A seems to be a function of two variables, and we have no techniques for

maximizing such a function. We must use the additional piece of information that

‘ 1 2w 5 200, or ‘ 5 200 2 2w. We substitute this expression for ‘ into the formula

for A. Thus our job is to maximize

AðwÞ5 ð200 2 2wÞw 5 200w 2 2w

; 0 # w # 100 :

Notice that we are careful to write down the range of values of w: This is necessary

to apply the Bas ic Rule. (Because ‘ cannot be negative, the equation ‘ 1 2w 5 200

tells us that the greatest possible value for w is 100.)

Now A is a polynomial, so it is differentiable at all values of w. Also dA/dw 5

200 2 4w. Clearly, dA/dw vanishes at w 5 50. Thus w 5 50 is a critical point.

By the Basic Rule, the maximum occurs at either the critical point w 5 50 or at

one of the endpoints w 5 0orw 5 100. To determine which, we calculate the value

of A(w) at each of these three points: A(0) 5 0, A(50) 5 5000, and A(100) 5 0.

Clearly, the maximum occurs when w 5 50. For this value of w , we calculate

‘ 5 200 2 2 50 5 100.

INSIGHT

Even this straightforward example contains all the major ingredients of

the examples that we will see in this section. Let’s outline them:

1. Determine the function f to be maximized or minimized.

2. Identify the relevant variable(s).

3. If f depends on more than one variable, ﬁnd relationships among the variables that

will allow substitution into the expression for f. The methods developed in this chapter

require you to obtain a function of one variable to be maximized or minimized.

4. Determine the set of allowable values for the variable (this is usually an interval).

5. Find all places where the function is not differentiable, all places where the derivative

is zero, and the endpoints. These are the points to test.

6. Use the First Derivative Test, or simply substitute in values as in Example 2,

to determine which of the points found in Step 5 solves the maximum-minimum

problem being studied.

⁄ EXAMPLE 3 A swimmer is 600 m straight out from a landmark on shore,

as shown in Figure 4. She wants to meet some friends who are 800 m down the

beach from the landmark. The swimmer can swim at a rate of 100 m/min and run on

the beach at the rate of 200 m/min. Toward what point on shore should she swim to

minimize the time it takes for her to join her friends?

Solution

Step 1. The function to be minimiz ed is the time T that

it takes the swimmer to

swim and run to her friends.

x  R  800

600

Swimmer

FriendsLandmark

1000

m Figure 4

ᐉ  200  2w

Fence

House

A(w)

m Figure 3

4.4 Applied Maximum-Minimum Problems 309

Step 2. The relevant variables are S, the distance swum, and R, the distance run.

Then the time spent swimming is S/100, and the time spent running is

R/200. Therefore

T 5

100

200

: ð4:4:1Þ

Step 3. Let x be the distance between the point where the swimmer hits the beach

and the landmark. Then, by the Pythagorean Theorem,

x 5 ðS

2 600

1=2

Also, x 1 R 5 800, or

R 5 800 2 x 5 800 2 ðS

2 600

1=2

Substituting this expression for R into equation (4.4.1) gives

TðSÞ5

100

800 2 ðS

2 600

1=2

200

: ð4:4:2Þ

Step 4. From Figure 4, the swimmer cannot swim any less than her 600 m distance

from the shore, nor more than the hypotenuse length,

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

600

1 800

,or

1000, of the larger right triangle in Figure 4. Therefore the range of values

for S is 600 # S # 10 00.

Step 5. The function T is differentiable at all points of (600, 1000), and we compute

100

ð1=2ÞðS

2 600

21=2

 2S

200

200 ðS

2 600

1=2



2ðS

2 600

1=2

2 S



200 ðS

2 600

1=2

This expression can vanish only if

2ðS

2 600

1=2

5 S

4ðS

2 600

Þ5 S

5 4  600

Thus the only root of dT /dS in the interval (600, 1000) is S 5 400

ﬃﬃﬃ

. This

critical point and the endpoints S 5 600 and S 5 1000 are the candidates for

the minimum we seek.

Step 6. Using equation (4.4.2), we calculate that T (600) 5 10, T (1000) 5 10, and

Tð400

ﬃﬃﬃ

Þ5 4 1 3

ﬃﬃﬃ

 9:196 , 10:

Thus S 5 400

ﬃﬃﬃ

gives the minimum. The value of x that we seek is

therefore x 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð400

ﬃﬃﬃ

2 600

5 200

ﬃﬃﬃ

: ¥

310 Chapter 4 Applications of the Derivative

INSIGHT

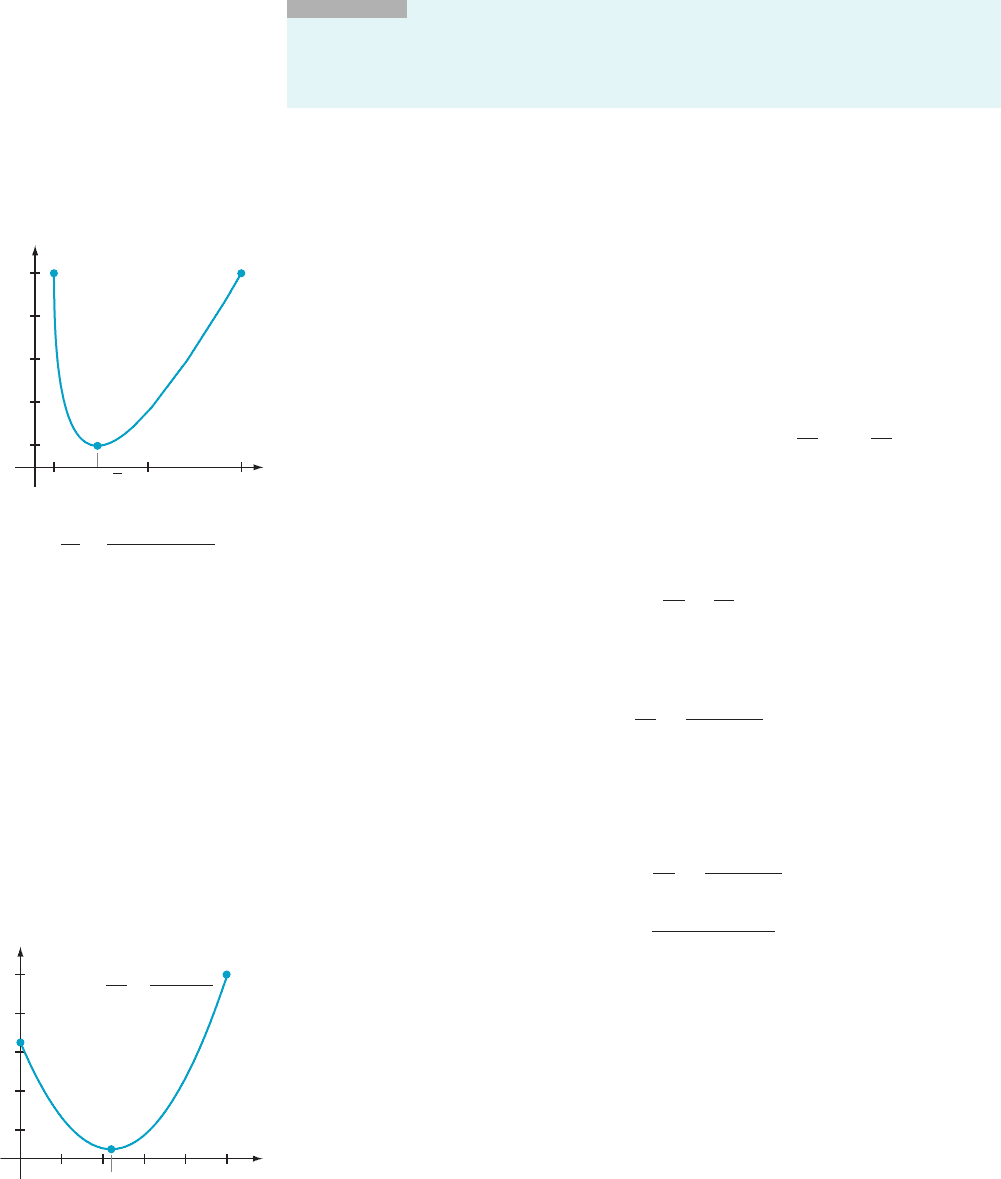
The graph of T from Example 3 appears in Figure 5. By repeatedly

zooming in on the low point of the graph, we can approximate the coordinates

(692.8, 9.196). A numerical algorithm for approximating extreme values is described in

the instructions for Exercises 61 and 62.

Examples with the

Solution at an Endpoint

⁄ EXAMPLE 4 A 10-inch piece of wire can be bent into a circle or a square,

or it can be cut into two pieces. In this case, a circle will be formed from the ﬁrst

piece and a square from the other. What is the maximal area that can result?

Solution

Step 1. The function to be maximized is the sum of the two areas (one of which

will

be 0 if the wire is not cut). Call this function A.

Step 2. The relevant variables are the lengths c (for the part of the wire that will

form the circle) and s (for the part of the wire that will form the square). If

the circle is made from the piece of length c, then the circumf erence of the

circle is c so that the radius of the circle is c/(2π). Therefore

Area of the circle 5 π radius

5 π 



2π



4π

The square is then manufactured from the piece of wire of length s. The

perimeter of the square is then s, and the side length is s/4. The area of the

square is (s/4)

,ors

/16. In conclusion, the function that we need to

maximize is

A 5

4π

Step 3. The variables c and s are related by the equation c 1 s 5 10, or s 5 c 2 10.

Substituting this into the formula for A g ives

A 5

4π

ðc 2 10Þ

: ð4:4:3Þ

Step 4. Clearly 0 # c # 10 because the wire is 10 inches long.

Step 5. The function A is a polynomial hence is differentiable everywhere. The

only candidates for the maximum we seek are the endpoints 0 and 10 and

the zeros of A

. Now

ðcÞ 5

4π

2ðc 2 10Þ

ð4 1 πÞc 2 10π

8π

The only root of A

or c 5 10π/(4 1 π)  4.399. This number is certainly in [0, 10]; hence, it is a

critical point.

Step 6. Referring to equation (4.4.3), we see that A (0) 5 25/4 5 6.25, A (10) 5 25/π C

7.958, and A (10π/(4 1 π)) 5 25/(4 1 π) C 3.501. Clearly the greatest area is

achieved when c 5 10,orwhenweusetheentirewiretomakeacirclebutno

square. The plot of equation (4.4.3), shown in Figure 6, conﬁrms our

analysis.

Our next example appears to be quite similar to Example 3. However, there is

a surprising and instructive difference.

600 800

1000

10.0

9.8

9.6

9.4

9.2

400



m Figure 5

TðSÞ5

100

800 2 ðS

2 600

1=2

200

1028

4.399

A  

(c  10)

m Figure 6

4.4 Applied Maximum-Minimum Problems 311

⁄ EXAMPLE 5 AjoggerisatpointP, 4 miles due south of point O.His

destination, point R, is 6 miles due east of O. He can run along roads from P to O and

from O to R at the rate of 5 miles per hour. Or he can hike across the ﬁeld from P to a

point Q at the rate of 3 miles per hour and then follow the road to point R at the rate

of 5 miles per hour (see Figure 7). How quickly can the jogger get from P to R?

Solution

Step 1. The function to be minimized is the sum of the times required to run from

P to Q and

from Q to R. Let us call this total time T.

Step 2. Let x be the distance of Q from O.

Step 3. When x 5 0, the runner jogs 4 miles north and then 6 miles east, all at

5 mph. His total time is 2 hours along this route. Thus T (0) 5 2. Now

suppose that x . 0. The distance of Q to R is 6 2 x, an d the time required to

jog this distance is (6 2 x)/5. By the Pythagorean Theorem, the distance of

P to Q is

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

, and the time required to hike this distance is

(

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

)/3. Thus the time T required for the journey is

TðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

6 2 x

when 0 , x # 6. (All values of T (x) are stated in hours.)

Step 4. Clearly 0 # x # 6.

Step 5. We calculate

ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

5x 2 3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

for 0 , x , 6. In order that T

(x) 5 0, we must have 5x 5 3

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

,or

25x

5 9(16 1 x

), or 16x

5 9 16. The positive solution is x 5 3. The can-

didates for the location of an extremum are therefore 3 and the endpoints

0 and 6.

Step 6. Becau se T

(x) , 0 for x in the interval (0, 3), and T

(x) . 0 in the interval

(3, 6), we deduce that T decreases on (0, 3) and increases on (3, 6). If T has

a minimum, then it must occur at x 5 3orx 5 0 because T is discontinuous

at x 5 0. In fact, T (0) 5 2 hr and

Tð3Þ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 3

6 2 3

 2:2667 hr:

We conclude that T (0) 5 2 is the minimum time in which to get from

P to R.

INSIGHT

The graph of T from Example 5 appears in Figure 8. Notice that T is

discontinuous. The Extreme Value Theorem therefore does not apply to T, and we

cannot be certain, prior to our analysis, that T has any extreme value on [0, 6]. In fact,

T does not assume a maximum value, but, as we have found, T does assumes a minimum

value on [0, 6].

Examples 1, 4, and 5 demonstrate that checking the endpoints is not simply an

academic exercise. As we have seen, the solution to a perfectly reasonable problem

can occur at an endpoint.

6  x

m Figure 7

615432

2.6

2.4

2.2

2.0

3415

T(x)

m Figure 8

312 Chapter

4 Applications of the Derivative

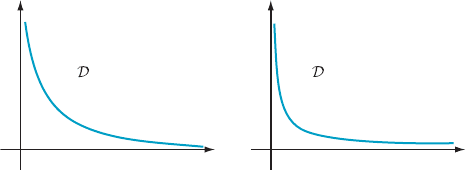
Proﬁt Maximization Let p be the price of a product, and let x denote the number of units of that product

that are sold. For an ordinary item, if the price p increases, then the sales level x

decreases. In other words, x is a decreasing function D of p:

x 5 DðpÞ: ð4:4:4Þ

Equation (4.4.4) is called the demand equation and the function D is known as the

demand function. Because D is a decreasing function, it has an inverse:

p 5 D

ðxÞ: ð4:4:5Þ

The plot of equation (4.4.5) with price measured along the vertical axis is called a

demand curve (see Figure 9).

The cost C (x) of pro ducing x units of a product includes ﬁxed costs, which are

independent of the number of units produced. For example, if a new automobile

motor is produced, then there will be design and testing costs that are the same

regardless of how many engines are manufacture d. There will also be incremental

costs that rise with each additional unit produced. For example, each new motor

requires a certain amount of raw materials, labor, and plant costs. The derivative

(x) is called the marginal cost (as discussed in Section 3.9 of Chapter 3). In a

simple model, each additional item produced will require an incremental cost equal

to m. In this model, the cost function is given by

CðxÞ5 C

|{z}

fixed costs

1 m  x

|ﬄ{zﬄ}

ðmarginal costÞðquantityÞ

Notice that, in this model, the marginal cost is the constant m. Marginal cost,

however, is often nonconstant.

The total revenue R is the number of units sold times the price per unit. Thus

R 5 x p. Equations (4.4.4) and (4.4.5) allow us to express revenue in terms of price

or quantity:

R 5 x D

ðxÞ or R 5 DðpÞp: ð4:4:6Þ

The proﬁt P is equal to revenue less cost. That is, P 5 R 2 C. By using equati ons

(4.4.4), (4.4.5), and (4.4.6), we can write P in terms of either x or p:

P 5 x D

ðxÞ2 CðxÞ or P 5 DðpÞp 2 C



DðpÞ



: ð4:4:7Þ

Determining the value p that maximizes proﬁt is clearly an important business

problem.

p 

1

(x)

x  (p)

m Figure 9 Equivalent representations of the demand equation

4.4 Applied Maximum-Minimum Problems 313

⁄ EXAMPLE 6 Suppose that the total dollar cost for producing x copies of a

particular book is C (x ) 5 12000 1 3x. Past experience indicates that the number x

of books sold is related to price p by the demand equation x 5 6000 (1 2 p/30). How

should the book be priced to optimize proﬁt?

Solution

Step 1. We are to maximize the proﬁt function P 5 D(p) p 2 C (D(p))

given in

line (4.4.7).

Step 2. The variables are the book pric e p and the number x of books sold.

Step 3. The demand equation x 5 D(p) 5 6000 (1 2 p/30) expresses x in terms of p.

Substituting this formula for D(p) in the equation for the proﬁt function

results in

P 5 DðpÞp 2 C



DðpÞ



5 6000



1 2



 p 2



12000 1 3  6000



1 2



After expanding and combining terms, we ﬁnd that

PðpÞ5 6600p 2 200p

2 30000

is the function to be maximized.

Step 4. The domain for the function P is the set of all positive p.

Step 5. The domain of P, namely the open interval (0,N), has no endpoint.

Because P is differentiable at all points in its domain, the only critical

points are the zeros of dP/dp 5 6600 2 400p. Thus p 5 6600/400 5 33/2 is

the unique critical point of P.

Step 6. Because dP/dp . 0forp , 33/2 and dP/dp , 0forp . 33/2, the First Deri-

vative Test tells us that proﬁt is maximized when p 5 33/2, or $16.50.

An Example Involving a

Transcendental

Function

⁄ EXAMPLE 7 Mr. Woodman is viewing a 6-foot-long tapestry that is hung

lengthwise on a wall of a 20 ft by 20 ft room. The bottom end of the tapestry is 2

feet above his eye level (see Figure 10). At what distance from the tapestry should

Mr. Woodman stand to obtain the most favorable view? That is, for what value of x

is angle α maximized?

Solution

Step 1. From Figure 10, we see that cot (α 1 ψ) 5 x/8,

or α 5 arccot (x/8) 2 ψ.

Step 2. The variables that appear in our formula for α are x and ψ.

Step 3. The variable ψ is related to x by the equation cot (ψ) 5 x/2, or

ψ 5 arccot (x/2). Substituting this value for ψ in the formula for α obtained

in Step 1, we obtain α 5 arccot ( x /8) 2 arccot (x/2). This is the function of x

that we are to maximize.

Step 4. The variable x is in the range (0, 20). (In practice, Mr. Woodman might not

be able to approach the wall with the tapestry or the opposite wall so

closely. If the remainder of our analysis were to turn up a value of x close

to 0 or 20, then we would need to be more accurate about the domain.)

Step 5. The domain of the function to be maximized does not contain an endpoint.

Because α is differentiable at all points of its domain, the only critical

points are the zeros of dα/dx. Using formula (3.10.11), we have,

dα

526

ðx

2 16Þ

ð4 1 x

Þð64 1 x

526

ðx 1 4Þ

ð4 1 x

Þð64 1 x

ðx 2 4Þ :

Thus x 5 4 is the unique critical point of P.

␺

␣

m Figure 10

314 Chapter

4 Applications of the Derivative