Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Step 6. From the formula for dα/dx, we see that

dα

526

ð1 Þ

ð1 Þð1 Þ

ð2Þ. 0 for x , 4and

dα

526

ð1Þ

ð1Þð1Þ

ð1 Þ, 0 for x . 4:

Thus α is an increasing function of x on (0, 4) and a decreasing function

of x on (4, 20). It follows that x 5 4 ft is the optimal distance at which

Mr. Woodman should stand.

QUICK QUIZ

1. True or false: If f is continuous on [a, b], then its maximum and minimum

must occur at critical points of the function.

2. True or false: If f is deﬁned and continuous on [1, 5], if f is differentiable on

the intervals (1, 2) and (2, 5), and if f

(3) 5 0, then the maximum value of f (x)

must be among the numbers f (1), f (2), f (3), and f (5).

3. True or false: If f is deﬁned and continuous on [2, 4], if f (2) 5 0 and f (4) 5 3,

and if there is no x in the interval (2, 4) for which f

(x) 5 0, then the maximum

value of f (x) must be 3.

4. Calculate the minimum values of f (x) 5 x 1 100/x on the intervals [1, 5],

[5, 12], and [12, 20].

Answers

1. False 2. True 3. False 4. 25, 20, 61/3

EXERCISES

Problems for Practice

c Solve each of the maximum-minimum problems in Exer-

cises 1220. Some may not have a solution, whereas others

may

have their solution at the endpoint of the interval of

deﬁnition. b

1. A

rectangle is to have perimeter 100 m. What dimensions

will give it the greatest area?

2. What positive number plus its reciprocal gives the least

sum?

3. What ﬁrst quadrant point on the curve xy

5 1 is closest to

the origin?

4. Find the longest vertical chord between the curves y 5

/3 2 3x

/2 1 2x 2 3/4 and y 5 3x

/4 2 15x

1 5x,0# x # 3.

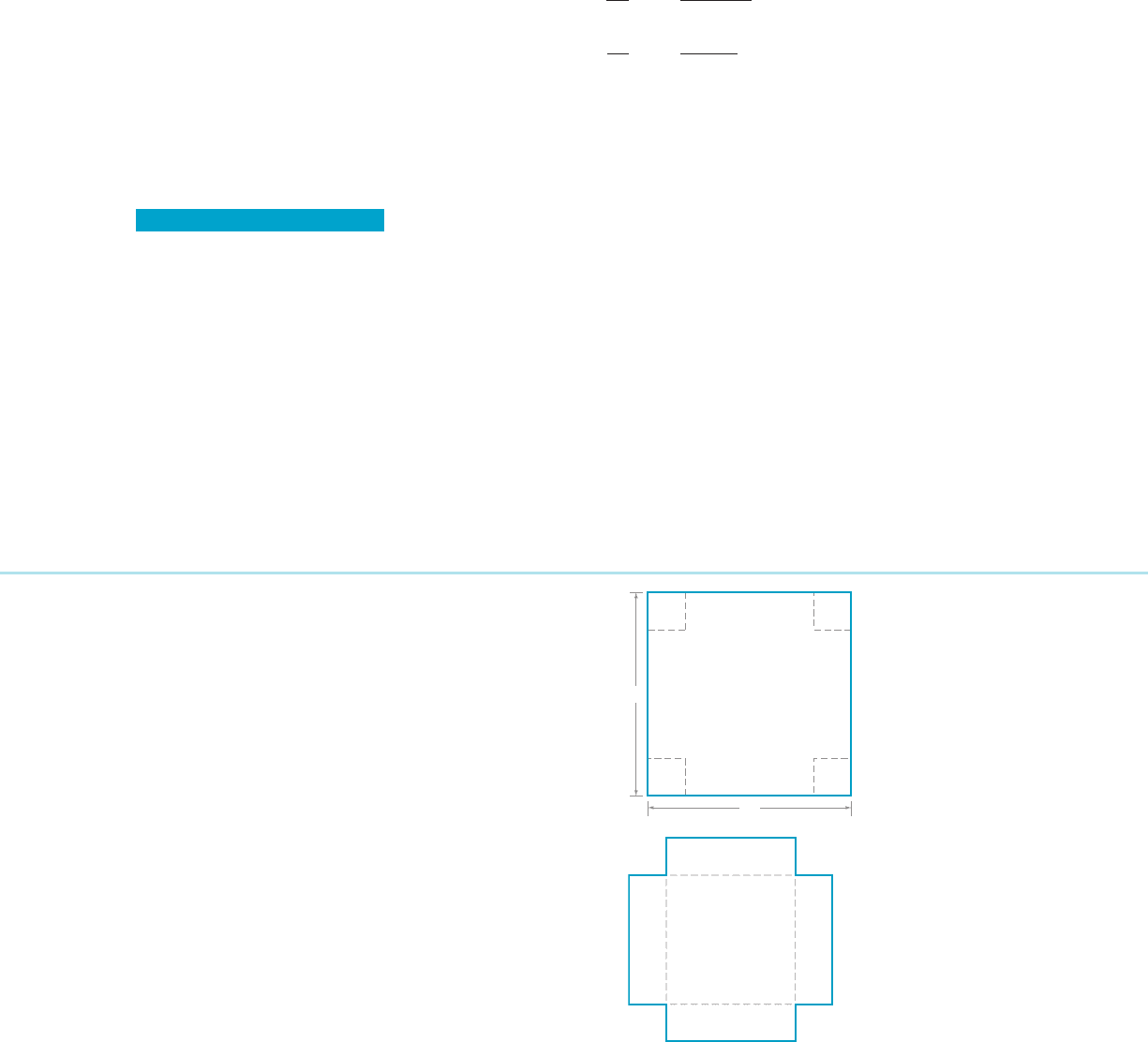
5. A box (with no lid) is to be constructed from a sheet of

cardboard by cutting squares from the corners and folding

up the sides (Figure 11). If the original sheet of cardboard

measures 20 inches by 20 inches, then what should be the

size of the squares removed to maximize the volume of the

resulting box?

6. Of all right triangles with hypotenuse 100 cm, which has

greatest area?

m Figure 11

4.4 Applied Maximum-Minimum Problems 315

7. A line with negative slope passes through the point (1, 2)

and has x-intercept a and y-intercept b. For what slope is

the product ab minimized?

8. A cylindrical can is constructed with tin sides and an

aluminum top and bottom. If aluminum costs 0.2 cents

per square inch, if tin costs 0.1 cents per square inch, and

if the can is to hold 20 cubic inches, what dimensions will

minimize the cost of the can?

9. Which nonnegative number exceeds its cube by the

greatest amount?

10. A right triangle is to contain an area of 50 cm

. What

dimensions will minimize the sum of the lengths of its two

legs?

11. A printed page is to have 1 inch margins on all sides. The

page should contain 8 square inches of type. What

dimensions of the page will minimize the area of the page

while still meeting these other requirements?

12. A church window will be in the shape of a rectangle

surmounted by a semi-circle (Figure 12). The area of

the window is to be 15 square meters. What should be the

dimensions of the window to minimize the perimeter?

13. A rectangle has its base on the x-axis, and its upper

corners are on the graph of y 5 4 2 x

. What dimensions

for the rectangle will give it maximal area?

14. A box with square base and rectangular sides is being

designed. The material for the sides costs 10 cents per

square inch and that for the top and bottom costs 4 cents

per square inch. If the box is to hold 100 cubic inches,

then what dimensions will minimize the cost of materials

for the box?

15. An open-topped rectangular planter is to hold 3 m

. Its

concrete base is square. Each brick side is rectangular. If

the unit cost of brick is twelve times that of concrete,

what dimensions result in the cheapest material cost?

16. What is the right triangle of least area that can be

inscribed in a circle of radius 3 meters?

17. A pentagonal shape consisting of a rectangle adjoining an

equilateral triangle (as in Figure 13) is to enclose 9801

. What base length will minimize the perimeter?

18. What is the rectangle (with sides parallel to the axes) of

greatest area that can be inscribed in the ellipse

1 4y

5 16?

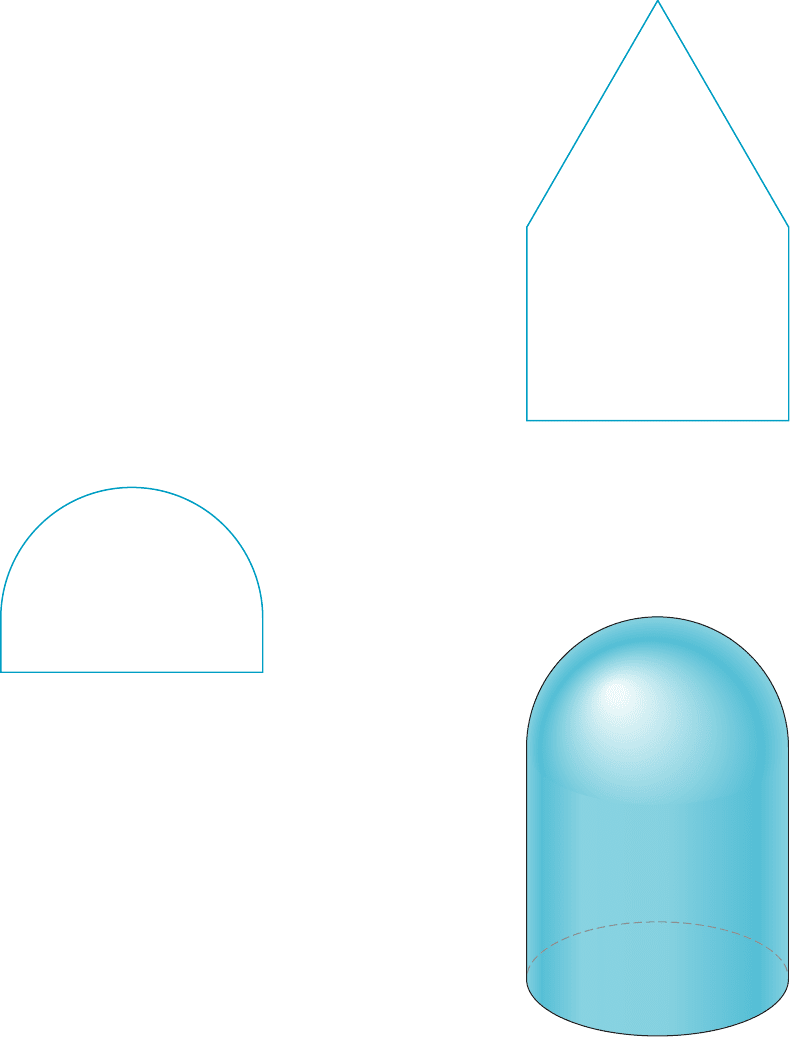
19. A cosmetic container is to be in the shape of a right circular

cylinder surmounted by a hemisphere (see Figure 14). If

the surface area is 5π square inches, what is the greatest

volume that this container can hold?

20. Assume that if the price of a certain book is p dollars,

then it will sell x copies where x 5 7000 (1 2 p/35).

Suppose that the dollar cost of producing those x copies is

15000 1 2.5x. Finally, assume that the company will not

Area  15

m Figure 12

Area  100

m Figure 13

m Figure 14 Cylinder surmounted by hemisphere

316 Chapter 4 Applications of the Derivative

sell this book for more than $35. Determine the price for

the book that will maximize proﬁt.

c In each of Exercises 21224, a cost function c and

form of the demand equation are given. Calculate the sales

level x that maximizes proﬁts. b

21. C (x) 5 1000 1 2x, D

(x) 5 1602 2 8x

22. C (x) 5 800 1 3x, D

(x) 5 26403 2 12x

23. C (x) 5 1200 1 8x, D ( p) 5 51 2 p/8

24. C (x) 5 7000 1 x, D ( p) 5 2402 2 2p

c In each of Exercises 25234, ﬁnd the absolute minimum

value

and absolute maximum value of the given function on

the given interval. b

25. f (x) 5 x

1 x;[21, 1]

26. f (x) 5 x

1 3x

2 45x 1 2; [26, 4]

27. f (x) 5 x

2 3x

/2 1 2; [21, 3]

28. f (x) 5 x

2 5x

;[22, 3]

29. f (x) 5 x (x 1 2)

;[23, 1]

30. f (x) 5 ( x

2 3)/(x 1 2); [23/2, 1]

31. f (x) 5 4x 1 9/x; [1, 2]

32. f (x) 5 x 2 4

ﬃﬃﬃ

; [1, 3]

33. f (x) 5 e

2 x;[21, 1]

34. f (x) 5 x

;[22, 3]

Further Theory and Practice

35. The relationship between the speed s of cars making their

way through a tunnel at a constant rate and the number x

of cars per km is expressed by the equation s 5 α 2 βx,

where α is a positive constant that carries the units of

km/hr, and β is a positive constant that carries the units

of km

/hr. What value of x results in the greatest number

of cars passing through the tunnel per hour?

36. A rectangle is to have one corner on the positive x-axis,

one corner on the positive y-axis, one corner at the origin,

and one corner on the line y 525x 1 4. Which such rec-

tangle has the greatest area?

37. Prove the Maximum Proﬁt Principle: Marginal revenue

) equals marginal cost C

) at the production

level x

that maximizes proﬁt.

38. The ﬁxed cost of producing a certain compact disc is $12000.

The marginal cost per disc is $1.20. Market research and

previous sales suggest that the demand function for this

particular disc will be x 5 19000 2 600p. At what production

level x

is the marginal cost equal to the marginal revenue?

Verify that proﬁt is maximized when x 5 x

39. If the cost of producing x units of a commodity is C (x),

then the average cost

C(x) of producing those x units is

C(x) 5 C(x)/x. Prove the Minimum Average Cost Prin-

ciple: When minimized, the average cost equals the

marginal cost.

40. A right circular cone of height h and base radius r has

volume πr

h/3 and lateral surface area πr

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 h

. What

is the greatest volume that such a cone can have if its

surface area, including the base, is 2π?

41. In a model for optimizing the angle of release θ of a

basketball shot, suppose that a and b are positive con-

stants. Let θ

be the value of θ in the interval (arctan (b/a),

π/2) for which

f ðθÞ5



asin ðθÞcosðθÞ2 b cos

ðθÞ



is minimized. What is tan (θ

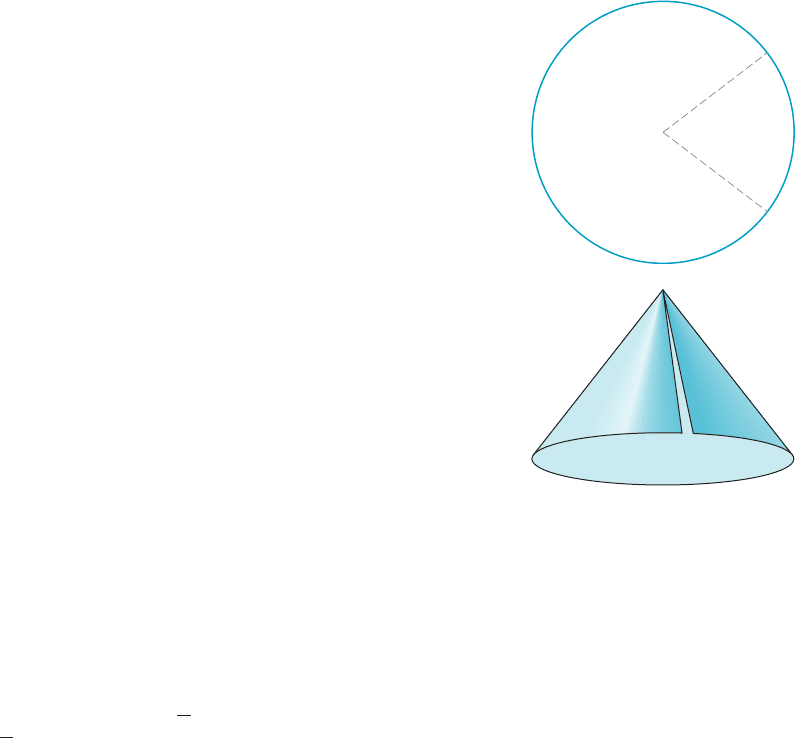
42. A piece of paper is circular in shape, with radius 6 inches.

A sector is cut from the circle and the two straight edges

taped together to form a cone (see Figure 15). What angle

for the sector will maximize the volume inside the cone?

43. A wire of length L can be shaped into a circle or a square,

or it can be cut into two pieces, one of which is formed

into a circle and the other a square. How is the minimum

total area obtained?

44. A wire of length L can be shaped into a (closed) semi-

circle or a square, or it can be divided into two pieces.

With one, a (closed) semicircle is formed and with the

other a square. Find the largest and smallest areas that

are possible.

m Figure 15

4.4 Applied Maximum-Minimum Problems 317

45. A wire of length L can be shaped into a (closed) semi-

circle or a circle. The wire can also be divided into two

pieces, with one piece forming a (closed) semicircle, and

the other, a circle. Find the largest and smallest areas that

are possible.

46. A battery that produces V volts with internal resistance

r ohms is connected in series to an external device with

resistance R ohms. The power output of the battery is then

R/(r 1 R)

.WhatvalueofR results in maximum power?

47. The drag on an airplane at a given altitude is given by

(a 1 b/v

) v

where a and b are positive constants, and v is

the velocity of the plane. At what speed is drag minimized?

48. In a certain process, the optimal time t for removing an

object from a heat source x units away is obtained by

maximizing

H 5

ﬃﬃ

exp





Here A and c are positive constants. What value of t

maximizes H?

49. The potential energy of a diatomic molecule is U 5

A (b/r

2 1/r

), where A and b are positive constants, and r

is the inter-atomic distance. What value of r minimizes U?

50. Carpenters will need to carry rods of various lengths

around a hall corner as shown in Figure 16. One hall is 6

feet wide, and the other is 8 feet wide. Ignoring the

thickness of the rod, and assuming that the rod is carried

parallel to the ﬂoor, determine the longest rod that the

carpenters will be able to carry around the corner.

51. A garden is to be bounded on one side by part of a river that

is shaped in a circular arc of radius 80 feet. The other three

sides will be straight fencing at right angles. The conﬁg-

uration is shown in Figure 17. Suppose that 100 feet of fence

is available. Carry out the steps for determining the largest

possible garden, but do not solve for the critical points.

52. When a person coughs, air pressure in the lungs increases,

and the radius r of the windpipe decreases from the normal

value ρ. Units can be chosen so that the ﬂow F through the

windpipe resulting from a cough is then given by

FðrÞ5 ðρ 2 rÞr

for 0 , r # ρ. What value of r results in the most productive

cough?

53. In Figure 18, B is a vascular branch point on a main artery

from the heart H. The branch angle θ 2(0, π/2) deter-

mines the resistance Ω to blood ﬂow to the organ O along

the path HBO according to

ΩðθÞ5

a 2 bcotðθÞ

sinðθÞ

For what value of cos ( θ) is resistance minimized?

54. (E. V. Huntington’s problem) A circular pool has radius r

and center at point O. Suppose that Earl is at point P at

the edge of the pool. He wishes to get to the diametrically

opposite point R in the least amount of time. He can swim

from P to Q and then run to R. Suppose that Earl’s

maximum swimming speed is u, and his maximum run-

ning speed is v. Let θ be the angle +OPQ.

a. Find an expression f (θ), 0 # θ # π/2 for the time

required for Earl to swim from P to Q in a straight line

and then to run from Q to R along the edge of the pool.

b. Show that if u , v, then f has one critical point in the

interval (0, π/2), and this critical point corresponds to a

maximum time.

c. Show that if u $ v, then f has no critical point in the

interval (0, π/2).

d. For which values of the parameters u and v does θ 5 0

give the minimum time? For which values of the para-

meters u and v does θ 5 π/2 give the maximum time?

e. How quickly can Earl get from P to R?

55. (V

. L. Klee’s problem) A rectangle is to be formed by

300 m of fencing of which a 100 m straight length is already

in place. The additional 200 m can be used to form the

three other sides or some of it can be used to extend the

existing length. How large can the enclosed region be?

c Exercises 56258 concern the most economical

dimensions

of a cylindrical tin can that holds a pre-

determined volume V. b

Rod

m Figure 16

Fence

River

m Figure 17

m Figure 18

318 Chapter

4 Applications of the Derivative

56. What are the dimensions if the amount of metal used in

the can is to be minimized? Express your answer as a

height h to radius r ratio.

57. (P. L. Roe’s problem) When the circular top and bottom

is cut from a large sheet of metal, there will be wastage.

Thus the amount of metal necessary to make a can is

actually larger then the amount of metal used in the can

itself. Suppose that the top and bottom circles are each

cut from squares whose side length is the diameter of the

circle. What is h/r when the amount of metal (including

wastage) is minimized?

58. (Continuation of P. L. Roe’s problem) Suppose that

the metal necessary to make the cylindrical can is

ﬃﬃﬃﬃﬃﬃﬃ

1 2π rh, including wastage. In forming the can, a

side join of length h and two circular joins of length 2πr

each are necessary. If a length k join costs the same as

a unit area of the metal, then the total cost C of pro-

duction is

C 5 4

ﬃﬃﬃ

1 2πrh 1 ð4πr 1 hÞ=k:

Write C as a function of r, and ﬁnd an equation for the

critical point of C. Show that there are constants a, b, c,

and d such that

ark 1 b

crk 1 d

when r is the critical point. In the case of very inexpensive

side joins (k-N), what is the approximate ratio h/r?In

the case of very expensive side joins (k-0), what is the

approximate ratio h/r?

59. Suppose that a uniform rod of length ‘ and mass m can

rotate freely about one end. If a point mass 6 m is

attached to the rod a distance x from the pivot, then the

period of small oscillations is equal to

2π

ﬃﬃﬃﬃﬃ



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

‘

1 18x

12x 1 ‘

For what value of x is the period least?

60. A volume V

of gas is held at pressure p

in a reservoir.

The gas is discharged through a nozzle of opening area A

into a region at lower pressure p. Then the rate of dis-

charge (in units of weight/time) is given by

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2gγ

γ 2 1





2=γ





ðγ11Þ=γ



where γ is the adiabatic constant of the gas. What is p/p

when the rate of discharge is greatest?

61. When a boat travels through open water, it creates a trailing

wedge of interior angle 2β

in which there is constructive

interference between waves. This is known as the Kelvin

wedge. The value of tan (β

) is the maximum value of

tan ðαÞ

2 1 tan

ðαÞ

Show that sin (β

) 5 1/3. (The Kelvin wedge therefore

encloses an angle of about 39



, independent of the speed

of the boat.)

62. A road is to be built from P 5 (0, b)toQ 5 (a, 0). The cost

of new road construction is c

per unit distance. There is an

existing straight road from the origin (0, 0) to Q.Totake

advantage of this existing route, highway engineers are

considering building a road from P to some point R 5 (c,0)

on the existing road. In that case, the existing road between

R and Q must be upgraded to handle the increased trafﬁc

ﬂow. The cost of this upgrade is c

per unit distance where

, c

. Determine the minimum cost route.

Calculator/Computer Exercises

63. Find the absolute minimum value and absolute maximum

value of

f ðxÞ5

1 sinðxÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2x 1 2

; 24 # x # 4:

64. Suppose that the cost function for producing a certain

product is C (x) 5 100000 1 1000

ﬃﬃﬃ

1 x

=40: Find the

production level x

at which average cost C(x) 5 C (x)/x is

minimized. What is

C(x

)? What is the marginal price at

this production level?

65. Two heat sources separated by a distance 10 cm are located

on the x-axis. The heat received by any point on the x-axis

from each of these sources is inversely proportional to the

square of its distance from the source. Suppose that the

heat received a distance 1cm from one source is twice that

received 1 cm from the other source. What is the location

of the coolest point between the two sources?

66. Suppose that, for a beam of length 11 meters, the

deﬂection from the horizontal of a point a distance x from

one end is proportional to

2 33x

1 1331x.

Determine the point at which the deﬂection is greatest.

67. Supposes that a shotputter releases the shot at height h,

with angle of inclination α, and initial speed v. Then the

horizontal distance R that the shot travels is given by

R 5

sinð2αÞ1 v

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sin

ð2αÞ1 8ghcos

ðαÞ

Use a computer algebra system to ﬁnd the value of α that

maximizes R.

68. Let α

denote the solution of tan(α

) 5 1/3 in (0, π/2). Plot

EðαÞ5

tanðαÞ



1 2 3tanðαÞ



3 1 tanðαÞ

for 0 , α # α

. Use the plot of E to ﬁnd the maximum

value of E (α) to three decimal places. Calculate E

(α).

Show that E (alpha) is maximized when α satisﬁes

4.4 Applied Maximum-Minimum Problems 319

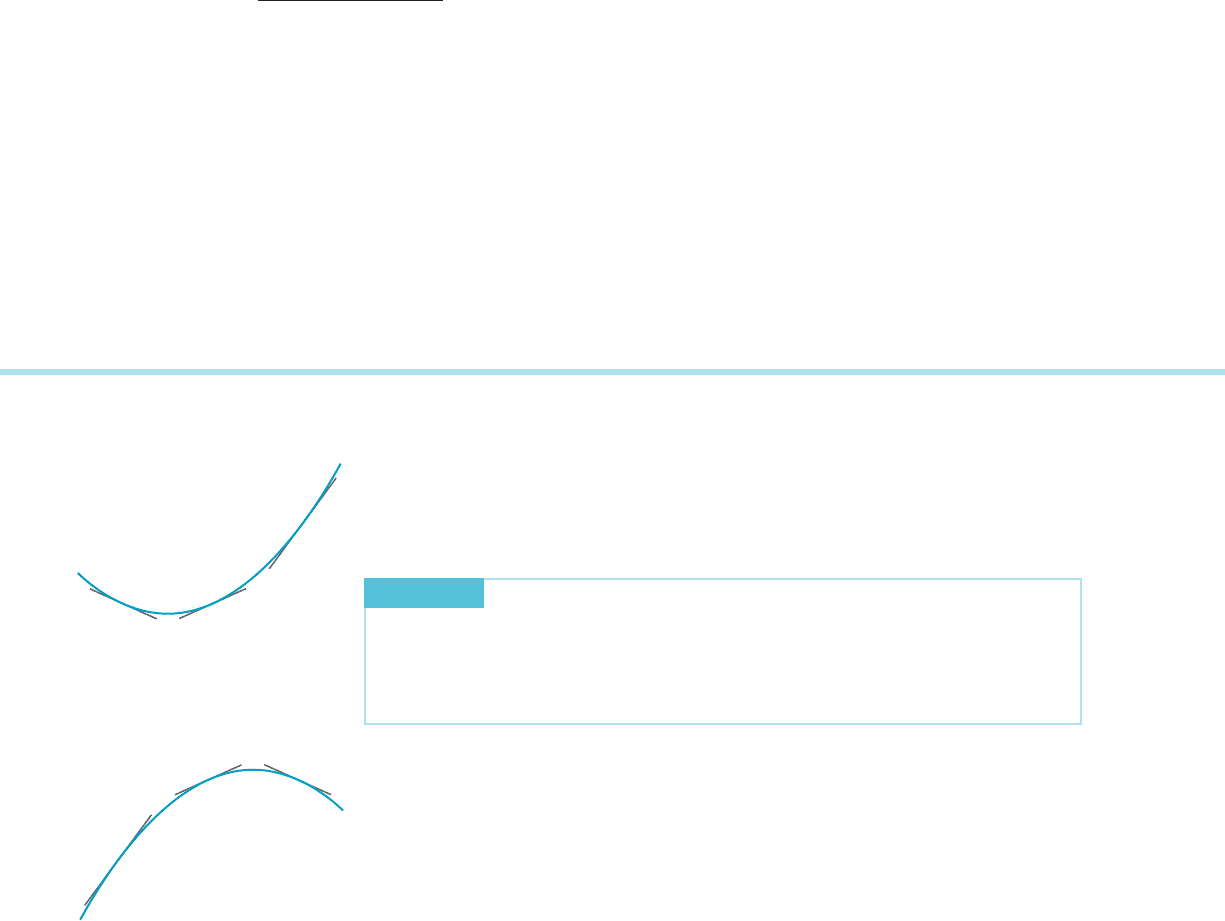
tan (α)

1 6 tan (α) 2 1 5 0.

Solve for tan(α) and ﬁnd the exact maximum value of

E (α). (This example, with E representing the efﬁciency

of a screw jack, μ the coefﬁcient of friction, and α the

pitch, arises in mechanical engineering.)

69. A tetramer is a protein with four subunits. In the study of

tetramer binding, the equation

Y 5

x 1 3x

1 3x

1 10x

1 1 4x 1 x

1 4x

1 10x

expresses a typical relationship between saturation Y and

ligand concentration x (x $ 0). Ordinarily, the variable

Y/x is plotted as a function of x. Explain why Y/x has an

absolute maximum value. Find it to three decimal places.

70. An underground pipeline is to be built between two

points P 5 (1, 4) and Q 5 (2, 0). The subsurface rock for-

mation under P is separated from what lies under Q by a

curve C of the form y 5 x

. The cost per unit distance of

laying pipeline from P to the graph of C is $5000. The unit

cost from the graph of C to Q is $3000. Assuming that the

pipeline will consist of two straight line segments, analyze

the minimum cost route.

c Exercises 71

and 72 utilize a minimization algorithm called

the Golden Ratio Search. Let ρ denote the Golden Ratio,

(

ﬃﬃﬃ

2 1)/2. Let r 5 ρ/(ρ 1 1)  0.381966. Suppose that f is

continuous on I 5 [a

, b

], has a minimum at c in (a

, b

), is

decreasing on (a

, c), and is increasing on (c, b

). (Such a

function is said to be unimodal.) Let Δx

5 b

2 a

5 a

1 r Δx

, and β

5 b

2 r Δx

. Calculate f (α

) and

f (β

). If f (α

) , f (β

), then let a

5 a

and b

5 β

. Otherwise,

let a

5 α

and b

5 b

. Repeat the procedure, letting

Δx

5 b

2 a

5 ρΔx

5 a

1 r Δx

, and β

5 b

2 r Δx

Calculate f (α

) and f (β

). (From the point of view of efﬁ-

ciency, it is useful to observe that one of these two values has

been computed in the last step: If a

5 a

,thenβ

5 α

;if

5 α

,thenα

5 β

.) If f (α

) . f (β

), then let a

5 a

and

5 β

.Otherwise,leta

5 α

and b

5 b

. Repeat the proce-

dure. After every step, the point c is in the interval I

5 [a

, b

Because b

2 a

5 ρ

n21

(b 2 a), the midpoint) c

5 (a

1 b

)/2

of I

satisﬁes |c 2 c

| # ρ

n21

(b 2 a)/2. Thus n can be chosen

large enough so that c

approximates c with any speciﬁed

accuracy. For the given function f on [0, 1]), locate c to two

decimal places. b

71. f (x) 5 3 2 2

ﬃﬃ

ﬃ

1 x

72. f (x) 5 2 1 x

2 sin (x)

4.5 Concavity

We have learned that we can use the sign of the ﬁrst derivative f

of a differentiable

function f to determine where the graph of f rises and where it falls. However, much

more can be said about the shape of a graph. In this section, we study the properties

of the graph of a function that are revealed by the second derivative.

DEFI NITION

Let the domain of a differentiable function f contain an open

interval I.Iff

(the slope of the tangent line to the graph) increases as x moves

from left to right in I, then the graph of f is said to be concave up on I (see

Figure 1). If f

decreases as x moves from left to right in I, then the graph of f is

said to be concave down on I (see Figure 2).

There are many ways to think about the concept of concavity. If P is a point on

the graph of f, then another way to deﬁne “f is concave up at P” is to require that

the tangent line to the graph at P lie below the graph just to the left and to the right

of P (see Figure 1). Similarly, “f is concave down at P” could be deﬁned to mean

that the tangent line to the graph at P lies above the graph just to the left and to the

right of P (as shown in Figure 2). Alternatively, we could deﬁne the graph of f to be

concave up (respectively down) if the graph of f lies below (respectively above)

every chord joining two points of the graph of f (see Figure 3). These other deﬁ-

nitions represent alternative points of view and will not be discussed further.

Slopes increasing

m Figure 1 The graph of f is

concave up.

Slopes decreasing

m Figure 2 The graph of f is

concave down.

320 Chapter 4 Applications of the Derivative

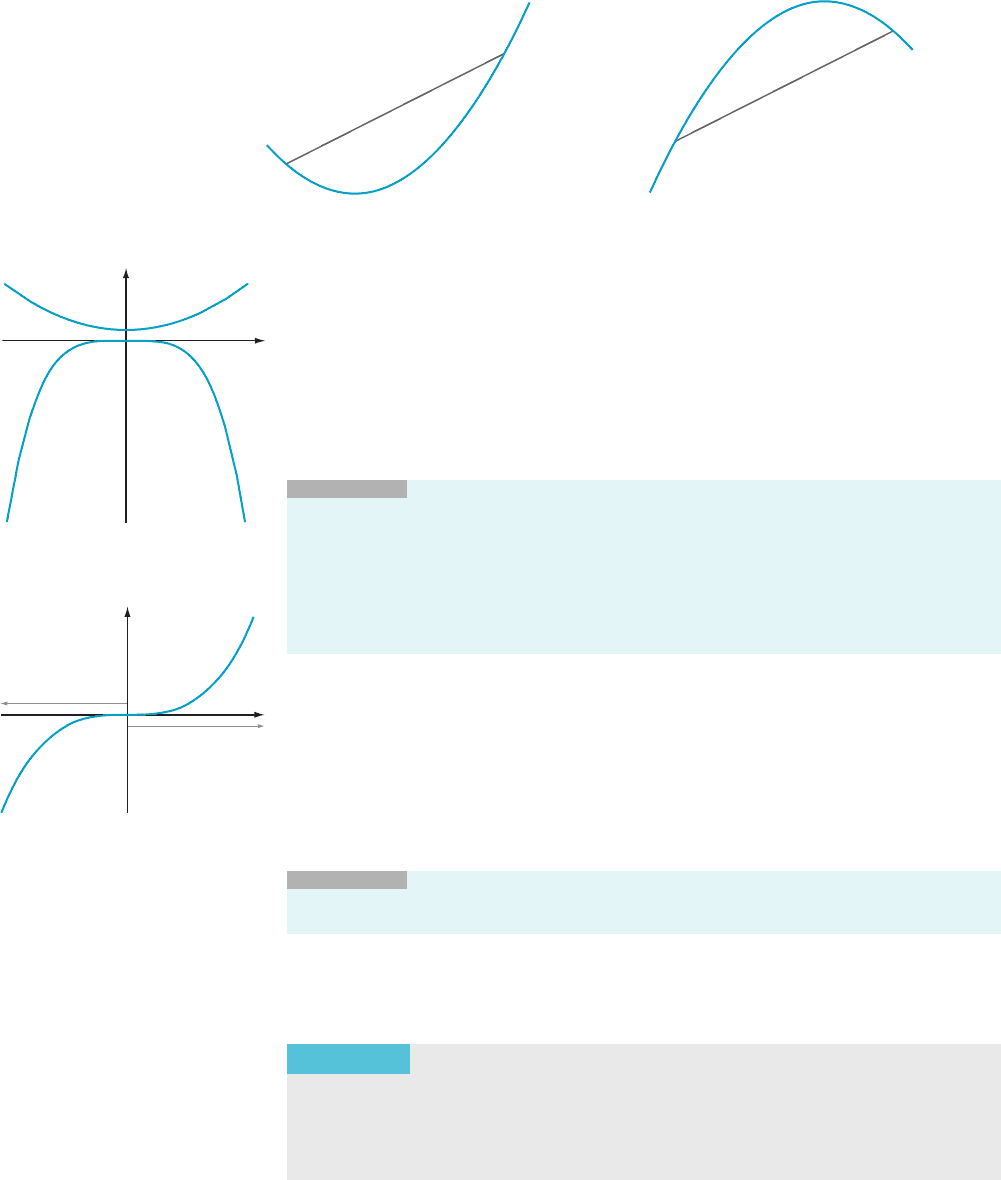
⁄ EXAMPLE 1 Discuss concavity for the graphs of f (x) 5 1 1 x

and

g (x) 52x

Solution We

calculate that f

(x) 5 2x, which is an increasing function on the entire

real line. Therefore the graph of f isconcaveupontheinterval(2N,N)(seeFigure4).

Similarly, the function g (x) 52x

satisﬁes g

(x) 524x

, which is a decreasing function

on (2N,N). Therefore the graph of g is concave down on (2N,N), as can also be seen

in Figure 4.

INSIGHT

At ﬁrst, it is easy to confuse “increase” and “decrease” of a given function

with the “concave up” and “concave down” properties of that function. The ﬁrst two

properties are independent of the second two. This means that a function can be

increasing and concave down, as the function g from Example 1 illustrates on the interval

(2N, 0), or decreasing and concave down (g on the interval (0,N)). Similarly, a function

can be increasing and concave up (the function f from Example 1 on the interval (0,N))

or decreasing and concave up ( f on the interval (2N, 0)).

⁄ EXAMPLE 2 Discuss concavity for the graph of the function f (x) 5 x

Solution First

of all, f

(x) 5 3x

. On the interval (0,N), the function f

(x) 5 3x

is increasing. Therefore the graph of f is concave up on (0,N). On the interval

(2N, 0), the function f

(x) 5 3x

is decreasing (because it becomes less and less

positive when x is negative and increasing). Therefore the graph of f is concave

down on (2N, 0) (see Figure 5).

INSIGHT

Example 2 shows that the graph of a function can be concave up on one

interval in its domain and concave down on another.

Using the Second

Derivative to Test

for Concavity

An important use of the second derivative is that it enables us to recognize the two

types of concavity.

THEOREM 1

(The Second Derivative Test for Concavity) Suppose that the

function f is twice differentiable on an open interval I.

a. If f

(x) . 0 for every x in I, then the graph of f is concave up on I.

b. If f

(x) , 0 for every x in I, then the graph of f is concave down on I.

Chords lie above the graph.

m Figure 3a The graph of f is concave up.

Chords lie below the graph.

m Figure 3b The graph of f is concave down.

f (x)  1  x

g(x)  x

m Figure 4

f (x)  x

Concave down

Concave up

m Figure 5

4.5 Concavity 321

Proof. Notice that f

5 ( f

)

. Thus the hypothesis that f

(x) . 0onI implies that

(x) is increasing on I, or, equivalently, that f is concave up. Similarly the

hypothesis that f

, 0 means that f

(x) is decreasing, or that f is concave down.

⁄ EXAMPLE 3 Apply the Second Derivative Test for Concavity to the

funct

ion f (x) 5 1/x.

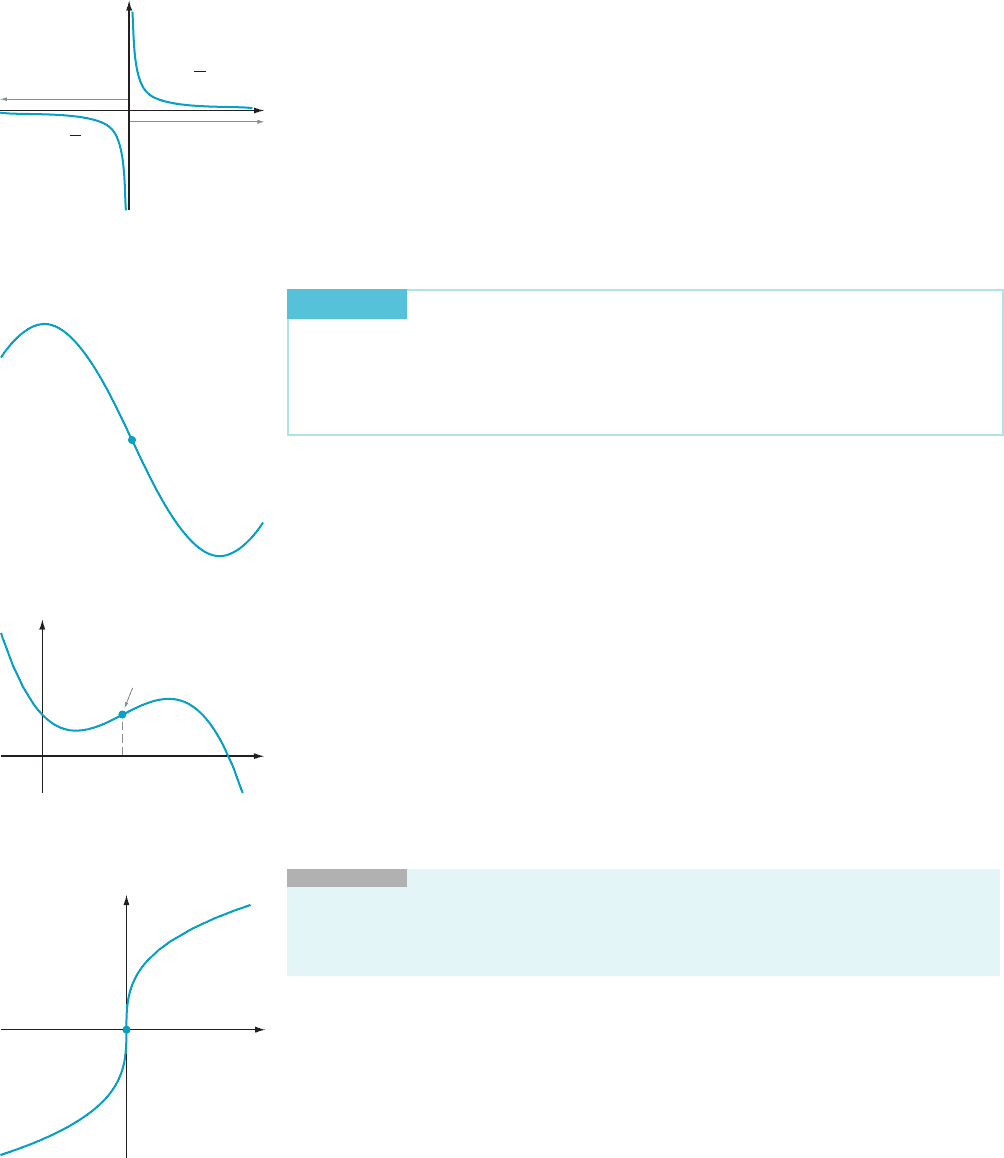
Solution P

rovided that x 6¼0, we calculate that f

(x) 521/x

and f

(x) 5 2/x

.Notice

that f

(x) . 0 on the interval (0,N). Hen ce, the graph of f is concave up on that interval.

Also f

(x) , 0ontheinterval(2N, 0). Therefore the graph of f is concave down on

that interval. A glance at the graph of f in Figure 6 conﬁrms these calculations.

Points of Inﬂection

DEFINITION

Let f be a continuous function on an open interval I. If the graph

of y 5 f (x) changes concavity (from positive to negative or from negative to

positive) as x passes from one side to the other of a point c in I, then the point

(c, f (c)) on the graph of f is called a point of inﬂection (or an inﬂection point).

We also say that f has a point of inﬂect ion at c (see Figure 7).

Notice that the funct ion f (x) 5 1 1 x

from Example 1 (graphed in Figure 4) is

concave up everywhere; hence, it has no points of inﬂection. Similarly, the function

g (x) 52x

of Example 1 (also in Figure 4) has no points of inﬂection because it is

concave down everywhere. On the other hand, the function f (x) 5 x

from

Example 2 (graphed in Figure 5) changes concavity at c 5 0, so (0, 0) is a point of

inﬂection. Finally, the graph of f ( x ) 5 1/x in Example 3 (graphed in Figure 6) is

concave down to the left of 0 and concave up to the right of 0; howeve r, 0 is not in

the domain of f,sof does not have a point of inﬂection at 0.

⁄ EX

AMPLE 4 Examine the graph of f (x) 5 x 2 (x 2 1)

for concavity and

points of inﬂection.

Solution We

calculate that f

(x) 5 1 2 3(x 2 1)

and f

(x) 526(x 2 1). Therefore

. 0 on the interval (2N,1) and f

, 0 on the interval (1,N). We concl ude that

the graph of f is concave up when x , 1 and concave down when x . 1. It follows

that f has a point of inﬂection at 1, as shown in Figure 8.

INSIGHT

The critical points of the function f from Example 4 are the solutions of

the equation f

(x) 5 1 2 3(x 2 1)

5 0. Using the Quadratic Formula, we see that the

critical points of f are located at x 5 1 6 1=

ﬃﬃﬃ

. However, the inﬂection point is at x 5 1.

Inﬂection points are not the same as critical points.

⁄ EXAMPLE 5 Examine the function f (x) 5 x

1/3

for concavity and points of

inﬂection.

Solution Fo

r x 6¼0, we have f

(x) 5 (1/3) x

22/3

and f

(x) 5 (22/9) x

25/3

. Therefore

. 0 on the interval (2N, 0), and f

, 0 on the interval (0,N). Thus the grap h of f is

concaveupon(2N, 0) and concave down on (0,N). Therefore f has a point of

inﬂection at 0. Notice that f is not differentiable at 0, but 0 is still an inﬂection point

because f is continuous and the concavity changes there (see Figure 9).

f (x) 

Concave down

Concave up

m Figure 6

Point of inflection

Concave up

Concave down

m Figure 7

(

)

 x 

(

x  1

)

Point of

inflection

Concave

down

m Figure 8

f (x)  x

13

Point of

inflection

Concave up

Concave down

m Figure 9

322 Chapter

4 Applications of the Derivative

Strategy for

Determining Points

of Inﬂection

Suppose that f has a point of inﬂection at c and that f

exists on both sides of c.

Because the graph of f is concave up on one side of c and concave down on the

other, we conclude that, as x moves from one side of c to the other, the value of

(x) changes sign. If f

(See Exer cise 81 of Section 4.3.) For instance, in Example 4, the inﬂection point of

the function f (x) 5 x 2 (x 2 1)

occurs at x 5 1, which is a root of the equation

(x) 5 0. We have also seen (in Example 5) that an inﬂection point can occur at a

point where f

(x) fails to exist. One of these two possibilities must occur at a point

of inﬂection. These considerations lead to the following strategy for determining

points of inﬂection of a continuous function f on an open interval I:

1. Locate all points of I at which f

5 0orf

is undeﬁned.

2. At each of these points, check to see if f

changes sign.

INSIGHT

It is a common error to think that f

of inﬂection for f. The function g (x) 52x

of Example 1 (Figure 4) shows why this

thinking is wrong: The graph of g is concave down everywhere, so there are no points of

inﬂection. In particular, g does not have a point of inﬂection at 0 even though g

(0) 5 0.

It may help to compare the tasks of locating points of inﬂection and local extrema.

Recall that local extrema occur at points where f

changes sign. To ﬁnd such points, we

must ﬁrst locate the points at which either f

5 0orf

does not exist; these are the points

at which f

might change sign. Having located these points, we must then check each one

of them to see if f

really does change sign. The search for points of inﬂection is com-

pletely analogous. Step 1 of the strategy—locating all points at which f

5 0orf

undeﬁned—produces the candidates that might be points of inﬂection. Step 2 of the

strategy—checking to see if f

changes sign—determines whether or not a candidate is an

actual point of inﬂection.

⁄ EXAMPLE 6 A function f is twice differentiable with f

(x) 5 (x 2 1)

(x 2 2) 

|x 2 3| for every x. Determine each x at which f has a point of inﬂection.

Solution By

hypothesis, f

(x) exists for every x. Therefore a point of inﬂection c

must satisfy f

Because the factors (x 2 1)

and |x 2 3| are nonnegative, we see that the sign of

(x) is the same as the sign of (x 2 2). This tells us that f

(x) changes sign only at

x 5 2 (as can be seen from the plot of f

in Figure 10). Therefore f has a point of

inﬂection only at x 5 2. Figure 11 contains the plot of one function f that has the

speciﬁed second derivative. It supports our conclusions.

The Second Derivative

Test at a Critical Point

We now apply our knowledge of concavity to the classiﬁcation of extrema.

THEOREM 2

(The Second Derivative Test for Extrema) Let f be twice dif-

ferentiable (both f

and f

exist) on an open interval containing a point c at

which f

a. If f

b. If f

c. If f

312

0.6

Concave

down

Concave up

0.4

0.2

f (x) 

x  3(x  3)



2(x  3)

 15(x  3)

 40x  80



m Figure 11 Point of inﬂection

1.0

2.0 3.0

f (x)  (x  1)

(x  2)x  3

m Figure 10

4.5 Concavity 323

Proof. The inequality f

)

is increasing at c. Because

must be going from negative to positive as x passes from

left to right through c. By the First Derivative Test, there is a local minimum at c.

Similarly, f

)

is decreasing at c. Because f

must be going from positive to negative as x passes from left to right through c.By

the First Derivative Test, there is a local maximum at c.

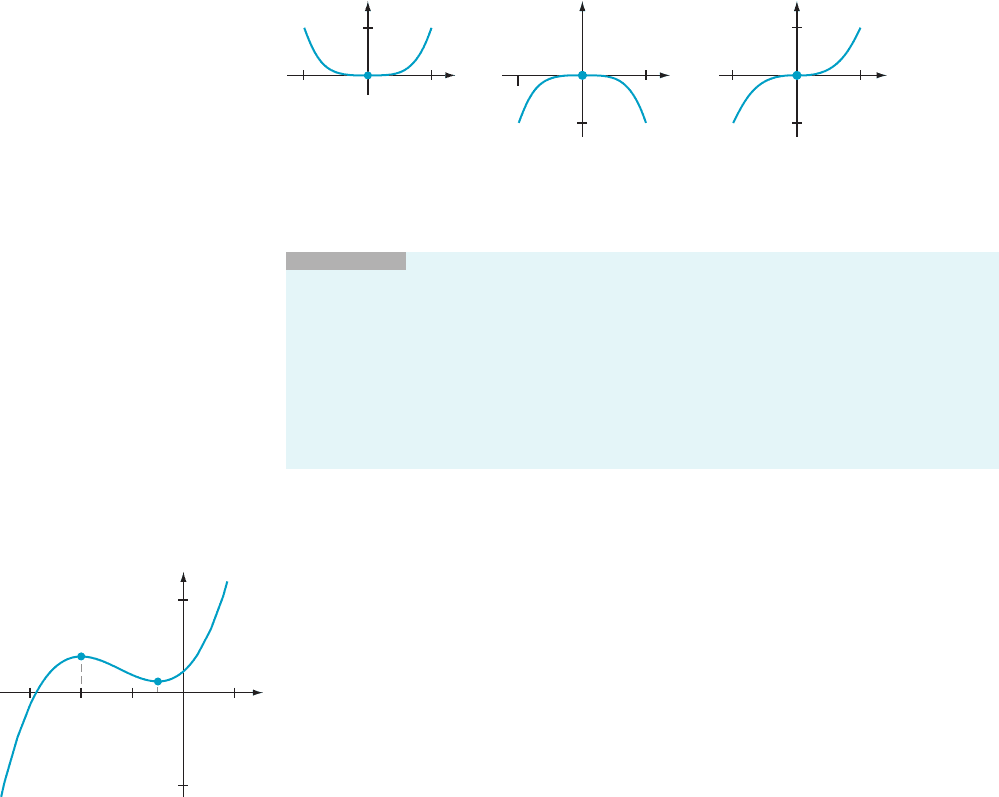
To understand the last stateme nt of the Second Derivative Test, notice that

(0) 5 0andf

(0) 5 0 for each of the three functions f (x) 5 x

, f (x) 52x

, and

f (x) 5 x

. The ﬁrst function obviously has a minimum at 0, the second has a

maximum, and the third has neither (see Figure 12). By themselves, the two

equations f

possible behaviors. ’

INSIGHT

At ﬁrst, it is surprising that f

the inequality f

minimum rather than a maximum. Similarly f

down at c, which indicates a maximum rather than a minimum.

Do not interpret the third part of the Second Derivative Test to mean that no con-

clusion is possible at all. We are able to analyze the behavior of each of the three

functions f (x) 5 x

, f (x) 52x

, and f (x) 5 x

at its critical point 0 even though the

Second Derivative Test is inconclusive for each of them.

⁄ EXAMPLE 7 Use Fermat’s Theorem and the Second Derivative Test for

Extrema to determ ine the local extrema of f (x) 5 2 x

1 15x

1 24x 1 23.

Solution This

function is a polynomial; it is deﬁned on the entire real line and is

differentiable everywhere. Therefore the only critical points are the zeros of f

.We

calculate

(x) 5 6x

1 30x 1 24 5 6(x 1 1)(x 1 4),

from which we see that the zeros of f

are 2 1 and 24. By Fermat’s Theorem, f can

have a local extremum only at these two poin ts. To use the Second Derivative Test

for Extrema, we calculate f

(x) 5 12x 1 30. Because f

(21) 5 18 . 0, the Second

Derivative Test for Extrema says that there is a local minimum at c 521. Because

(24) 5218 , 0, the Second Derivative Test for Extrema says that there is a local

maximum at c 524 (see Figure 13).

No local

extremum

f (x)  x

Local

minimum

11

1 1

1

Local

maximum

1

(

)

 x

m Figure 12 f

(0) 5 0 and f

(0) 5 0 for all three functions.

100

4 2 1

100

m Figure 13

324 Chapter

4 Applications of the Derivative