Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

b A LOOK BACK Although the Second Derivative Test for Extrema is convenient, it

does not supersede the First Derivative Test (Theorem 2 of Section 4.3). That is

because the First Derivative Test (part a) requires less computation than the Second

Derivative Test, (part b) can be applied when the second derivative does not exist,

and (part c) can be applied when the second derivative exists but is 0.

QUICK QUIZ

1. True or false: f

(4) 5 0 tells us that (4, f (4)) is a point of inﬂection for y 5 f (x).

2. True or false: f

(x) , 0 on (1, 5) and f

(x) . 0 on (5, 5.1) tells us that (5, f (5)) is

a point of inﬂection for y 5 f (x).

3. Suppose that f

(x) 5 (x 1 2)

(x 2 3). Does f (x) have a point of inﬂection at

x 522? At x 5 3?

4. True or false: f

(4) , 0 tells us that f (x) has a maximum at x 5 4.

5. True or false: f

(4) 5 0andf

(4) . 0 tell us that f (x) has a maximum at x 5 4.

Answers

1. False 2. True 3. No at x 522,

yes at x 5 3 4. False 5. False

EXERCISES

Problems for Practice

c In each of Exercises 1236, determine the intervals on

which the given function f is concave up, the intervals on

which f is concave down, and the points of inﬂection of f. Find

all critical points. Use the Second Derivative Test to identify

the points x at which f (x) is a local minimum value and the

points at which f (x) is a local maximum value. b

1. f (x) 5 x 2 4

ﬃﬃ

ﬃ

2. f (x) 5 1/x 2 1/x

3. f (x) 5

ﬃﬃﬃ

1 3/

ﬃﬃﬃ

4. f (x) 5 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 2 2

5. f (x) 5 x

1 54/x

6. f (x) 5 1/(x

1 1)

7. f (x) 5 x

1 9x

2 21x 1 15

8. f (x) 522x

1 12x

1 7

9. f (x) 5 2x

2 3x

2 12x 1 1

10. f (x) 5 x/(x 2 4)

11. f (x) 5 x

2 2x

2 9x

12. f (x) 5 x

2 8x

1 9

13. f (x) 5 3x

2 10x

1 15x 2 8

14. f (x) 5 2x

1 15x

1 30x

2 42

15. f (x) 5 x/(x

1 3)

16. f (x) 5 x/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

17. f (x) 5 ( x

2 1)/(x

1 1)

18. f (x) 5 ( x 1 1)

19. f (x) 5 cos (x) 1 x,0, x , 2π

20. f (x) 5 x/2 2 sin (x), 0 , x , 2π

21. f (x) 5 tan (x/2), 2π , x , π

22. f (x) 5 tan (x) 2x, 2π , x , π

23. f (x) 5 sin

(x), 0 , x , π

24. f (x) 5 x 2 e

25. f (x) 5 e

1 e

26. f (x) 5 xe

27. f (x) 5 x 2 ln (x)

28. f (x) 5 1/x 1 ln ( x)

29. f (x) 5 x

2 8ln(x)

30. f (x) 5 x 2 ln (x) 1 2/x

31. f (x) 5 x

1/3

(x 2 5)

32. f (x) 5 x

2/3

(x 2 4)

1/3

33. f (x) 5 x 1 1/2

34. f (x) 5 arctan (1 1 x

)

35. f (x) 5 arcsin (x) 2 x

, 21 , x , 1

36. f (x) 5 cosh (x) 2 2 exp (x)

Further Theory and Practice

c In Exercises 37242, the derivative f

of a function f is

given. Determine and classify all local extrema of f. b

37. f

(x) 5 x (x 2 1)

38. f

(x) 5 x

(x 2 1)

39. f

(x) 5 x

2 1

40. f

(x) 5 (x

2 1)

41. f

(x) 5 (x

2 4)

42. f

(x) 5 (x 2 1)(x 2 2)

(x 2 3)

(x 2 4)

c In Exercises 43248, the second derivative f

of a function

f is given. Determine every x at which f has a point of

inﬂection. b

4.5 Concavity 325

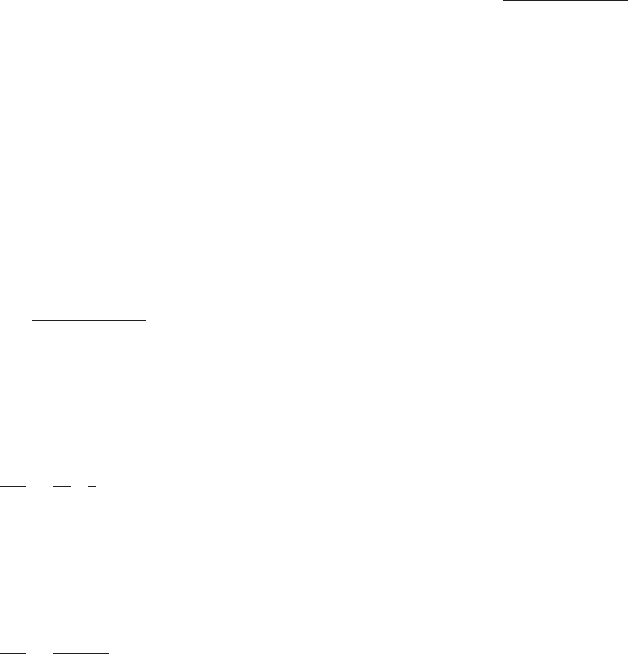
43. f

(x) 5 x (x 1 1)

44. f

(x) 5 x

(x 1 2)

45. f

(x) 5 x

1 4

46. f

(x) 5 (x

2 1)

47. f

(x) 5 (x

2 25)

48. f

(x) 5 x (x 2 1)

(x 2 2)

(x 2 3)

49. For a positive constant a, the Witch of Agnesi is the curve

whose equation is y 5 8a

/(4a

1 x

). Find the points of

inﬂection of this curve. On what intervals is this curve

concave up? Concave down?

50. Suppose that a function f has a point of inﬂection at c.

Can f have a local extremum at c?

51. Suppose that f (x) . 0 and f

(x) . 0 for all x. Describe the

concavity of f

52. Suppose that f and g are twice differentiable functions that

are concave up. Is f 1 g concave up? Is f g concave up?

53. Let k and c be positive constants. Suppose that a yeast

population has mass m that satisﬁes the inequalities

0 , m (t) , 2c and the differential equation

ðtÞ5 k  mðtÞð2c 2 mðtÞÞ

for all values of t. By completing the square on the right

side, determine the ordinate of the point of inﬂection of

the graph of y 5 m (t). Discuss the concavity of this graph.

54. For every positive x, the number W (x) is deﬁned to be the

unique positive number such that

W (x) exp (W (x)) 5 x.

The function x/W ( x) is known as Lambert’s W func-

tion. Show that

ðxÞ5

x 1 expðWðxÞÞ

Deduce that W is an increasing function, and show that

the graph of W is concave down.

55. Suppose that x and y are twice differentiable functions of

a parameter t. Show that



where Newton’s notation indicates differentiation with

respect to t.

56. Suppose that x and y are twice differentiable functions of

a parameter t. Use Exercise 55 to show that

€

y 2

€

xÞ

where Newton’s notation indicates differentiation with

respect to the parameter t.

57. Let a be a positive constant. One arch of the cycloid is

deﬁned by the equations x 5 a (t 2 sin (t)), y 5 a (1 2 cos

(t)) for 0 , t , 2π. Use the formula of Exercise 56 to

analyze the concavity of the graph. Identify any local

extrema.

58. Let C be the parametric curve deﬁned by x 5 t

2 1,

y 5 t

2 t for 2N, t ,N. Notice that the points of C cor-

responding to t 521, t 5 0, and t 5 1 lie on the x-axis. Use

the formula of Exercise 56 to show that C is concave up for

t . 0 and concave down for t , 0. Use these observations to

sketch C.

59. Let C be the parametric curve deﬁned by x 5 tan (t),

y 5 cos

(t) for 2π/2 , t , π/2. Use the formula of Exercise

56 to determine the interval on which C is concave down

and the intervals on which C is concave up. Notice that

0 , y # 1 with the maximum value occuring at the point

(0, 1). Calculate the horizontal asymptote of C. Use all

this information to sketch C.

c The formula

ðxÞj



11 f

ðxÞðÞ



3=2

measures the curvature of the graph of y 5 f (x) at the point

(x, f (x)). In Exercises 60263,

compute the curvature of the

given function. b

60. f (x) 5 x

1 x 1 2

61. f (x) 5 cos (x)

62. f (x) 5

ﬃﬃﬃ

63. f (x) 5 1/x

c In each of Exercises 64267, ﬁnd the point at which f has

maximum

curvature. (See the instructions to Exercises

60263.) b

64. f (x) 5 ln

(x)

65. f (x) 5 x

/3, 0 , x

66. f (x) 5 sin (x), 0 , x , π

67. f (x) 5 e

68. Show that the curvature of the circle x

1 y

5 r

is 1/r at

all points (x, y) with y 6¼0.

69. Assuming that the range of f is contained in the domain of

g, ﬁnd a formula for (g 3 f)

(c). Suppose that f and g are

concave up. What property of g ensures that g 3 f is also

concave up?

70. The product of labor f (n) and the marginal product of

labor (MPL) have been deﬁned in Section 4.3, Exercise

60. Economists generally assume that the graph of the

function f has a certain property. The three graphs that

appear in Figure 17 of Section 4.3 illustrate this property

in different ways. What is the property?

71. Let R (q) denote the revenue realized by selling q units of

an item. Let c (q) denote the total cost incurred in selling

those q units. Suppose that the proﬁt R2C is maximized

at q

. The second derivatives R

and C

are plotted in

Figure 14. Identify which curve is R

and which curve is

and explain your reasoning.

326 Chapter 4 Applications of the Derivative

Calculator/Computer Exercises

c In Exercises 72279, approximate the critical points and

inﬂection points of the given function f. Determine the

behavior of f at each critical point. b

72. f (x) 5 arcsin ((x 1 1)/(x

1 2))

73. f (x) 5 x/(1 1 e

)

74. f (x) 5 x

1 3x

2 2x 1 4

75. f (x) 5 x

2 2e

1 3x

76. f (x) 5 6x

2 45x

1 80x

1 30x

2 30x 1 2

77. f (x) 5 ( x

1 1)/(x

1 x 1 2)

78. f (x) 5 2 arctan (x) 2 arctan (x 1 1)

79. f (x) 5 tanh (x) 2 x

/(x

1 1)

80. For a function f that is twice differentiable, deﬁne C (x) 5

a signum( f

(x)), where a is a positive constant. Explain

how the graph of C may be used to determine the con-

cavity and the points of inﬂection of the graph of f.

Illustrate by plotting

f (x) 5 6x

1 x

2 60x

2 35x

1 120x

1 52x 1 160

and c (x) 5 300 signum( f

(x)) in the viewing window

[22.3, 2.8] 3 [2310, 310]. (The choice of 300 for a scales

the graph of C so that we can see it in the same viewing

window as f.)

4.6 Graphing Functions

Curve sketching is one of the most important techniques of analytical thinking. The

skills of creating and understanding graphs are used in all of the physical sciences and

many of the social sciences as well. In previous sections, we have learne d that certain

aspects of the graph of a function f can be determined from the ﬁrst and second

derivatives of f. We have seen that graphs of functions can have vertical asymptotes or

horizontal asymptotes or both. In this section, we will combine all these concepts and

use them to sketch the graphs of functions. Even if you have a graphing calculator or

software with graphing capabilities, the knowledge that you will gain in this section will

be useful. The best way to learn how to interpret a graph is to learn how it is created.

Basic Strategy of

Curve Sketching

The following steps can be used to sketch the graphs of an extensive range of

functions.

Basic Steps in Sketching a Graph

1. Determine the domain and (if possible) the range of the function.

2. Find all horizontal and vertical asymptotes.

3. Calcul ate the ﬁrst derivative, and ﬁnd the critical points for the function.

4. Find the intervals on which the function is increasing or decreasing.

5. Calcul ate the second derivative, and ﬁnd the intervals on which the function is concave up or concave down.

6. Identify all local maxima, local minim a, and points of inﬂection.

7. Plot these points, as well as the y-intercept (if applicable) and any x-intercepts (if they can be computed).

Sketch the asymptotes.

8. Connect the points plotted in Step 7, keeping in mind concavity, local extrema, and asymptotes.

If you follow this systematic procedure in sketching your graphs, you will ﬁnd

that you can handle a wide variety of interesting examples.

Units sold

Cost (dollars)

m Figure 14 Plots of R

and C

4.6 Graphing Functions 327

⁄ EXAMPLE 1 Graph the function f (x) 5 5x/(x 2 2)

Solution We

follow the outline just given:

1. The domain of f con

sists of all real numbers except 2. When x is near the point 2,

the function f (x) takes arbitrarily larg e positive values.

2. We notice that lim

x-1N

f ðxÞ5 lim

x-2N

f ðxÞ5 0: Therefore the line y 5 0isa

horizontal asymptote for the graph. Also lim

x-2

f ðxÞ51N: Therefore the line

x 5 2 is an upward vertical asymptote for f.

3. We calculate that

ðxÞ 5

ðx 2 2Þ

 5 2 5x  2ðx 2 2Þ

ðx 2 2Þ

25ðx 1 2Þ

ðx 2 2Þ

The ﬁrst derivative is deﬁned at all points of the domain of f. Because f

vanishes

at 22, this is the only critical point. In Step 6, we will determine whether or not f

has a local extremum at x 522.

4. The ﬁrst derivative can change sign only at 22 (the critical point) and 12 (the

point where f is undeﬁned). Bec ause f

(23) 521/25, we conclude that f

, 0on

the interval (2N, 22); hence f is decreasing there. Because f

(0) 5 5/4 . 0, we

conclude that f

. 0 on the interval (22, 2); hence f is increasing there. Finally,

because f

(3) 5225 , 0, we see that f

, 0 on the interval (2,N); hence f is

decreasing there.

5. The second derivative is

ðxÞ 5

ðx 2 2Þ

ð25Þ2 ð25ðx 1 2ÞÞ 



3ðx 2 2Þ



ðx 2 2Þ

10 ðx 1 4Þ

ðx 2 2Þ

Notice that the denominator of f

is always positive on the domain of f. Clearly

, 0 on the interval (2N, 24) because the numerator is; hence f is concave

down on that interval. Also f

(x) . 0 when x .24 (except at x 5 2, the point

where f, f

, f

are undeﬁned); hence f is concave up on each of the intervals

(24, 2) and (2,N).

6. Because f

(22) 5 5/64 . 0, there is a local minimum at the critical point x 522.

The point (22, f (22)) 5 (22, 25/8) will be labeled on our graph. From Step 5,

the concavity changes at x 524. Therefore f has a point of inﬂection at x 524.

The point (2 4, f (24)) 5 (24, 25/9) will be labeled on our graph. The concavity

does not change at x 5 2.

7. The y-intercept is (0, f (0)) 5 (0, 0). Because x 5 0 is the only solution to f (x) 5 0,

the point (0, 0) is also the only x-intercept. The points (0, 0), (22, 25/8), and

(24, 25/9) have been plotted in Figure 1.

8. The ﬁnal sketch of the graph of f is in Figure 1. All of the pe rtinent data are

labeled. Notice that we can deduce from all the information gathered that f has

an absolute minimum at x 522. There is no absolute maximum.

328 Chapter

4 Applications of the Derivative

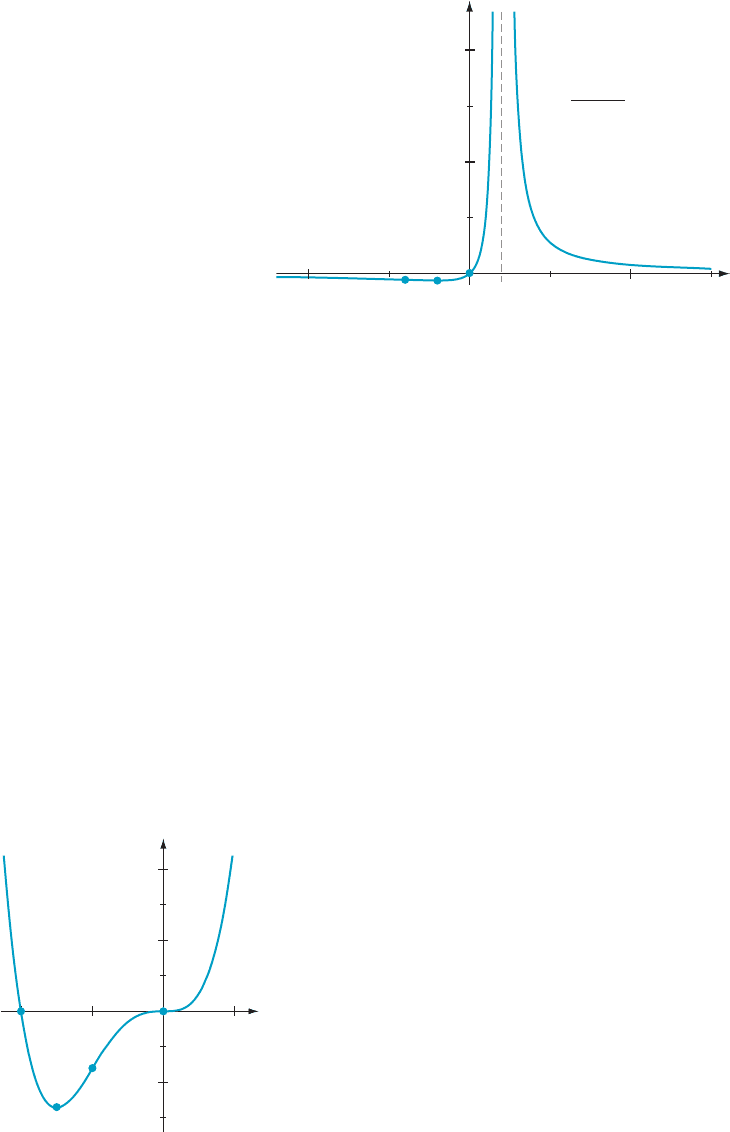
⁄ EXAMPLE 2 Sketch the graph of g (x) 5 4x

1 x

Solution

1. Because g is

a polynomial, the domain of g consists of all real numbers. When x

is large, the term x

forces g to take arbitrarily large positive values.

2. By the comment in Step 1, g has no ﬁnite limit as x-6N. Thus there are no

horizontal asymptotes. Also, g is continuous at every point because it is a

polynomial. Consequently, there are no vertical asymptotes.

3. We have g

(x) 5 12x

1 4x

5 4x

(3 1 x). Because g

(x) is deﬁned for all x, the

only critical points are the zeros of g

. These are 0 and 23. In Step 6, we will

determine whether g has a local extremum at either of these points.

4. From the formula for g

(x) in Step 3, we see that the ﬁrst derivative can change

sign only at 23 and at 0. Because g

(24) 5264 , 0, we conclude that g

, 0on

the interval (2N, 2 3). Therefore g is decreasing on (2N, 23). Because g

(21) 5

8 . 0, we conclude that g

. 0 on the interval (23, 0). Therefore g is

increasing on (23, 0). Because g

(1) 5 16 . 0, we conclude that g

. 0 on (0,N).

Therefore g is increasing on (0,N).

5. The second derivative is g

(x) 5 24x 1 12x

5 12x (2 1 x). From this formula, we

see that g

can change sign only at the points 0 and 22 where it vanishes. Because

(23) 5 36 . 0, we conclude that g

. 0 on the interval (2N, 22); hence, g is

concave up on (2N, 22). Because g

(21) 5212 , 0, we conclude that g

, 0on

the interval (22, 0); hence, g is concave down on (22, 0). Because g

(1) 5 36 . 0,

we conclude that g

. 0 on the interval (0,N); hence, g is concave up on (0,N).

6. By Step 5, we know that the concavity changes at 22 and at 0. These are the

inﬂection points of g. We will label the points (22, g (22)) 5 (22, 216) and

(0, g (0)) 5 (0, 0) on our graph. In Step 4, we saw that g

, 0 to the left of 23

and g

. 0 to the right of 23. Therefore a local minimum occurs at the critical

point 23. We will label the point (23, g (23)) 5 (23, 227) on our graph. We

have already noted that the other critical point 0 is an inﬂection point.

7. The intercepts are (0, 0) and (24, 0). They will also be labeled in our graph.

8. Figure 2 shows the sketch of the graph of g. All pertinent data have been

indicated. We can deduce that there is an absolute minimum at 23. There is no

absolute maximum.

(0, 0)

(4, 59)

Inflection

point

(2, 58)

Absolute

minimum

x  2

1010

f(x) 

(x  2)

m Figure 1

(3, 27)

Absolute minimum

Inflection

point

Inflection

point

(0, 0)

(4, 0)

(2, 16)

20

22

g(x)  4x

 x

m Figure 2

4.6 Graphing Functions 329

INSIGHT

In each of Examples 1 and 2, we stated that the information gathered

allowed us to determine that a particular point is an absolute minimum of the function

under consideration. The graphs of each function certainly support our conclusion about

these points. Note, however, that because a graph can only be given in a ﬁnite viewing

rectangle, the graphs cannot by themselves prove assertions concerning absolute

extrema. If you have not already done so, it will be instructive for you to explain

why (22, 25/8) must be an absolute minimum of the function f from Example 1 and why

(23, 227) must be an absolute minimum of the function g from Example 2.

⁄ EXAMPLE 3 Sketch the graph of f (x) 5 (4x 1 1)/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 3x 1 2

Solution

1. Because x

2 3x 1 2 5 (x 2 1)(x 2 2) is negative between its two roots, the

interval (1, 2) is not in the domain of f. The endpoints of this interval are also

excluded because the denominator is 0 at these values. The domain of f consists

of the union of the open intervals (2N, 1) and (2,N). The function f is con-

tinuous on these intervals.

2. By calculating lim

x-1

f ðxÞ5 N and lim

x-2

f ðxÞ5 N, we see that the vertical

lines x 5 1 and x 5 2 are upward vertical asymptotes. (It makes no sense to

consider lim

x-1

f ðxÞand lim

x-2

f ðxÞ because such limits involve x in the

interval (1, 2), which is not in the domain of f.) By writing

f ðxÞ5

xð4 1 1=xÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð1 2 3=x 1 2=x

jxj



4 1 1=x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 3=x 1 2=x

and noting that x/|x| 5 1 for 0 , x and x/|x| 521 for x , 0, we deduce that

lim

x-N

f ðxÞ5 4 and lim

x-2N

f ðxÞ524. The lines y 5 4 and y 524 are there-

fore horizontal asymptotes.

3. After some simpliﬁcation, we ﬁnd that

ðxÞ52

14x 2 19

ðx

2 3x 1 2Þ

3=2

Because f

is deﬁned for all x in the domain of f, the only critical points are the

zeros of f

. The expression

14x 2 19

ðx

2 3x 1 2Þ

3=2

has one zero, x 5 19/14, but this zero is not in the domain of f

since it is between

1 and 2 and therefore not in the domain of f. We conclude that f has no critical

points.

4. The denominator of f

(x) is always positive. The sign of f

(x)

is therefore the sign of its numerator 14x 2 19. Remembering that the domain of

f is (2N,1) , (2,N), we deduce that f

(x) . 0 for x , 1 and f

(x) , 0 for x . 2.

Therefore f is increasing on (2N, 1) and decreasing on (2,N).

5. After simpliﬁcation, we ﬁnd that

ðxÞ5



56x

2 156x 1 115

ðx

2 3x 1 2Þ

5=2



Note that f

exists at every point in the domain of f. Because 156

2 4 56 115 5

21424 , 0, the Quadratic Formul a tells us that f

has no real zeros.

330 Chapter 4 Applications of the Derivative

6. By Step 5, we know that there are no points of inﬂection. Because f

(0) . 0, we

deduce that the graph of f is concave up everywhere.

7. The intercepts (21/4, 0) and (0,

ﬃﬃﬃ

=2) and the vertical and horizontal asymp-

totes are plotted in Figure 3.

8. The ﬁnal sketch of the graph of f appears in Figure 3. There are no local

extrema. Notice that, alt hough f (x) .24 for all x in the domain of f, the

number 24 is not a value of f (x ) for any x. Therefore 24 is not the minimum

value of f.

Periodic Functions A function f is said to be periodic if there is a positive number p such that

f ðx 1 pÞ5 f ðxÞ; x 2 R: ð4:6:1Þ

The smallest nonnegative number p for which equation (4.6.1) is true is called the

period of f. The sine, cosine, secant, an d cosecant functions all have period 2π.

However, we observe that

tanðx 1 πÞ 5

sinðx 1 πÞ

cosðx 1 πÞ

sinðxÞcosð πÞ1 cosðxÞsinðπÞ

cosðxÞcosðπÞ2 sinðxÞsinðπÞ

sinðxÞð21Þ1 0

cosðxÞð21Þ2 0

sinðxÞ

cosðxÞ

5 tanðxÞ;

which shows that the the period of the tangent is either π, or possibly a smaller

number. However, because the derivative of tan (x) is sec

(x), which is positive on

(2π/2, π/2), we know that tan (x) increases on an interval of length π. Therefore

tan (x 1 p) 5 tan (x) is impossible for 0 # p , π . It follows that tan (x) has period π,

as does its reciprocal cot (x).

To graph a function f whose period is p, we plot f over the interval [0, p]and

then translate the plot of this restriction by p units (Figure 4). If f is continuous on

[0, p] then it attains a maximum value and a minimum value by the Extreme Value

Theorem. The next example illustrates these points.

10 5510

y  4

y  4

x  2x  1

(14, 0)

f(x) 

4x  1

 3x  2

(0,

22)



m Figure 3

1 cycle

3 cycles

p

m Figure 4

4.6 Graphing Functions 331

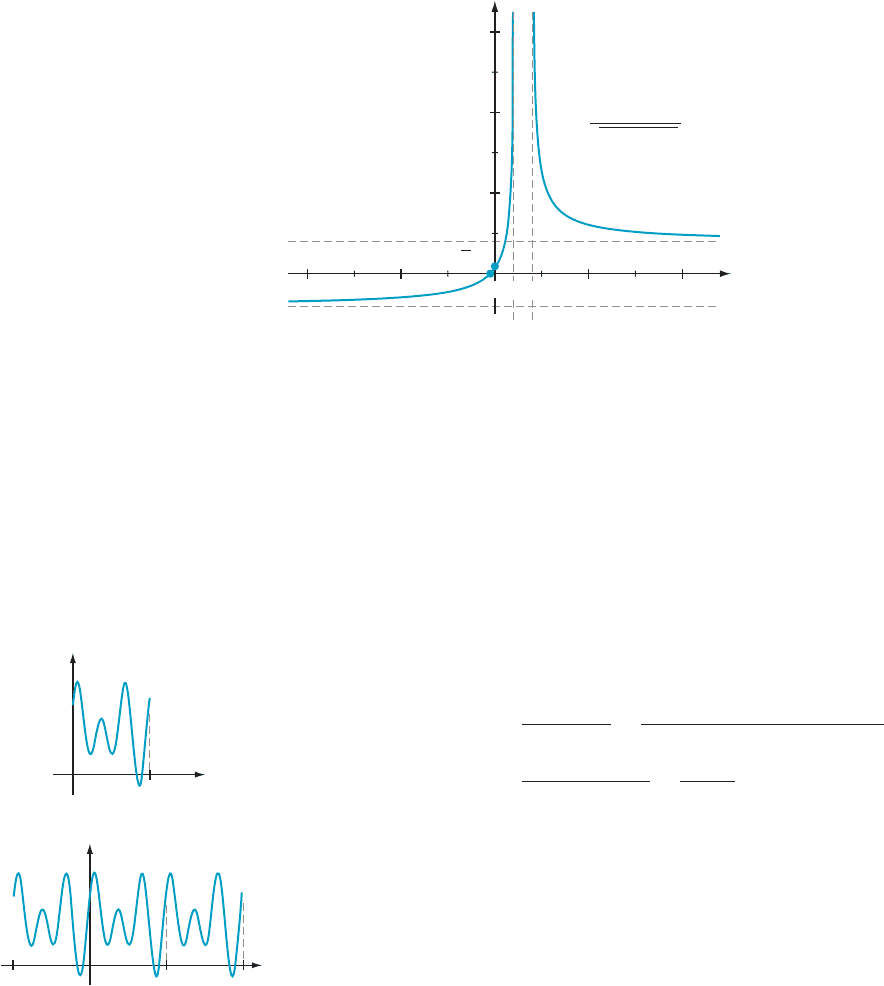
⁄ EXAMPLE 4 Sketch the graph of the function f (x) 5 sin (x)/(2 1 cos (x)).

Solution

1. The function f (x)

is deﬁned for all real x because its denominator is never zero.

Observe that f (x 1 2π) 5 f (x) for all x. This tells us that f is periodic, and the

entire graph of f is determined by the part that lies over [0, 2π].

2. Because f is continuous at every x, there are no vertical asymptotes. Because f is

periodic and nonc onstant, we conclude that f has no horizontal asym ptotes.

3. We calculate that

ðxÞ5

1 1 2 cosðxÞ

ð2 1 cosðxÞÞ

The zeros of f

occur when cos (x) 521/2. The solutions of this equation in the

interval [0, 2π] are x 5 2π/3 and x 5 4π/3.

4. Observe that the sign of f

(x) is the same as the sign of 1 1 2cos(x). This

expression is positive for x in the intervals [0, 2π/3) and (4π/3, 2π]; it is negative for

x in the interval (2π/3, 4π/3). Therefore f is increasing on [0, 2π/3) and (4π/3, 2π]

and f is decreasing on (2π/3, 4π/3).

5. After differentiation and algebraic simpliﬁcation, we ﬁnd that

ðxÞ522 sinðxÞ

ð1 2 cosðxÞÞ

ð2 1 cosðxÞÞ

Because the expressions 1 2 cos ( x ) and 2 1 cos (x) are nonnegative, we see that

the signs of f

(x) and sin (x) are opposite. Therefore f

(x) , 0 for 0 , x , π and

(x) . 0 for π , x , 2π. We conclude that the graph of f is concave down on the

interval (0, π) and concave up on the interval (π,2π).

6. Because the critical point 2π/3 is in the inte rval on which f

, 0, the Second

Derivative Test tel ls us that f (x) has a local maximum at x 5 2π /3. Similarly,

we see that f has a local minimum at 4π/3. From the formula for f

(x) that we

obtained in Step 5, we notice that the sign of f

(x) changes at each point where

sin (x) vanishes. Therefore the points 0, π, and 2π are the points of inﬂection that

f has in the interval [0, 2π].

7. The y-intercept is the origin. The x-intercepts are the points of the form (kπ,0)

where k is an integer. Because f (0) 5 0, f (2π/3) 5

ﬃﬃﬃ

=3; f (4π/3) 52

ﬃﬃﬃ

=3; and

f (2π) 5 0, we deduce that f has an absolute maximum value of

ﬃﬃﬃ

=3 and an

absolute minimum value of 2

ﬃﬃﬃ

=3:

8. Figure 5 contains a sketch of that part of the graph that lies over [0, 2π]. This portion

of the graph is repeated periodically in Figure 6, which shows four cycles of f.

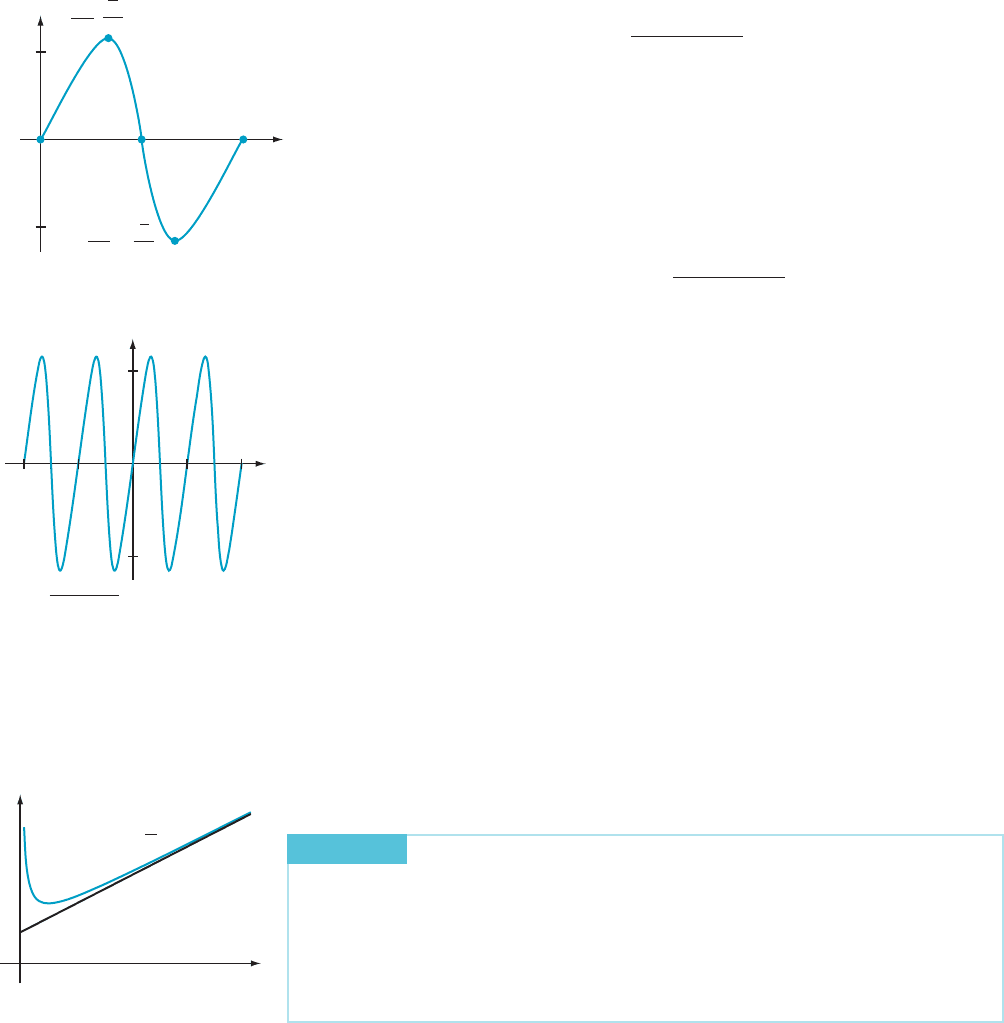
Skew-Asymptotes The line y 5 2x 1 3 and the graph of f (x) 5 2x 1 3 1 1/x are shown in Figure 7.

Notice that the graph of f becomes closer to the straight line y 5 2x 1 3asx-Nand

x- 2N. This leads to a deﬁnition.

DEFINITION

The line y 5 mx 1 b is a skew-asymptote of f if

lim

x-N

ðmx 1 b 2 f ðxÞÞ5 0

or if

lim

x- 2N

ðmx 1 b 2 f ðxÞÞ5 0:

Other terms for this line are slant-asymptote and oblique-asymptote.

0.5

0.5

(0, 0) (p, 0)

(2p, 0)

Point of

inflection

Absolute

minimum

Absolute

maximum



, 





m Figure 5

4p 2p 4p2p

0.5

(x) 

sin(x)

2  cos

(

)

m Figure 6

y  2x  3

f(x)  2x  3 

m Figure 7

332 Chapter

4 Applications of the Derivative

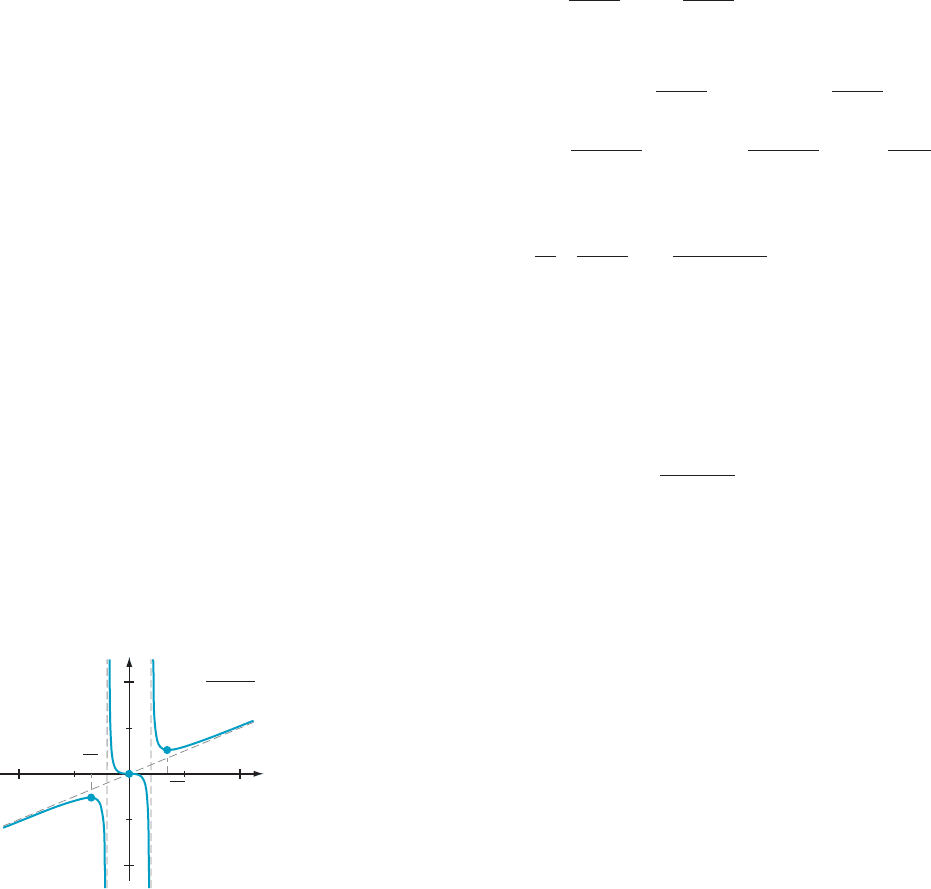
With the introduction of this concept, Step 2 of the eight basic steps of graph-

sketching should be expanded to include all asymptotes. The most common

situation in which a skew-asymptote occurs is in graphing a rational function with a

numerator of degree one more than its denominator. In this case, division allows us

to determine the skew-asymptote.

⁄ EX

AMPLE 5 Sketch the graph of f (x) 5 x

/(x

2 4).

Solution We

follow the outline given above:

1. The domai n of f co

nsists of all real numbers except x 512andx 522.

2. The lines x 5 2 and x 522 are vertical asymptotes. Because division gives us

2 4

5 x 1

2 4

;

we see that y 5 x is a skew-asymptote:

lim

x-6N

ðx 2 f ðxÞÞ 5 lim

x-6N



x 2



x 1

2 4



52 lim

x-6N

2 4

52 lim

x-6N

4x=x

1 2 4=x

524 lim

x-6N

1=x

1 2 4=x

524 

1 2 0

5 0:

3. We calculate that



2 4



ðx

2 12Þ

ðx

2 4Þ

The ﬁrst derivative is deﬁned at all points of the domain of f. Because f

vanishes

at 0 and 6

ﬃﬃﬃﬃﬃ

; these are the only critical points.

4. The ﬁrst derivative changes sign at 2

ﬃﬃﬃﬃﬃ

and

ﬃﬃﬃﬃﬃ

but not at 0. We see that

. 0 on the intervals ð2N; 2

ﬃﬃﬃﬃﬃ

Þ and ð

ﬃﬃﬃﬃﬃ

; NÞ. We see that f

, 0 on the

intervals ð2

ﬃﬃﬃﬃﬃ

; 22Þ; ð22; 2 Þ; and ð2;

ﬃﬃﬃﬃﬃ

Þ:

5. Differentiating the expression in Step 3, we ﬁnd that the second derivative of f is

ðxÞ5 8x

1 12

ðx

2 4Þ

The numerator x

1 12 is always positive and doesn’t affect the sign of f

. The

sign of f

can change only at a zero of f

or at a poin t where f

doesn’t exist.

There are three such points: x 5 0 is a zero of f

(x) and f

(x) doesn’t exist at

x 522 and x 5 2. To determine the sign of f

on the intervals (2N, 22), (22, 0),

(0, 2), and (2,N) , we need only evaluate f

at one point in each interval.

Because f

(23) 52504/125, f

(21) 5 104/27, f

(1) 52104/27, and f

(3) 5 504/

125, we deduce that f is concave up over the intervals (2 2, 0) and (2,N)and

concave down over the intervals (2N, 22) and (0, 2).

6. From Step 5, we know that the concavity changes at 22, 0, and 2. Because 22

and 2 are not in the domain of f, we see that (0, 0) is the only point of inﬂection.

From Step 4 we see that a local maximum occurs at 2

ﬃﬃﬃﬃﬃ

and a local min imum

ﬃﬃﬃﬃﬃ

7. The graph of f crosses the axes only at (0, 0). In Figure 8, we have plotted this

point together with the point of inﬂection and the local extrema. We have also

drawn in the vertical asymptotes and the skew-asymptote.

8. The ﬁnal sketch of the graph of f is in Figure 8. All of the pertinent data have

been indicated.

f(x) 

 4

1010

20

y  x

x  2

x  2





m Figure 8

4.6 Graphing Functions 333

Graphing Calculators/

Software

Graphing calculators and plotting software are convenient tools. However, we must

understand their limitations and, when necessary, be able to correct the plots that

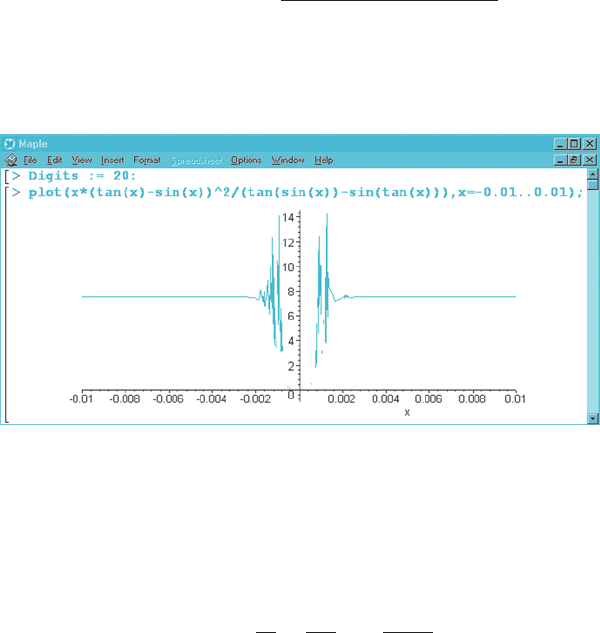
they render. Figure 9 is a screen capture in which a computer algebra system has

been used to plot

f ðxÞ5

xðtanðxÞ2sinðxÞÞ

tanðsinðxÞÞ2 sinðtanðx ÞÞ

over the interval [20.01, 0.01]. Even though 20 digits ha ve been carried in the

computation, a loss of signiﬁcance (Section 1.1) has resulted in a wildly inaccurate

plot. Although a computer algebra system allows us to increase the number of

digits until a reliable plot is attained, this resource may not be an option with a

graphing calculator. In this case, an important approximation technique of calculus

(to be learned in Chapter 8) shows that

f ðxÞ5

205

85403

42336

1 EðxÞ;

where the summand E (x) is negligible over the interval [20.1, 0.1]. By discarding

the term E (x), we obtain a good polynomial approximation that is easily and

accurately plotted. Although Figure 10 shows only one curve, we are actually viewing

both the plot of f, rendered using 40 digits, and the plot of y 5 15/2 2 205x

/42 1

85403x

/42336. The differences between the values of f (x) and the approximating

polynomial cannot be detected in the plot.

There are many situations in which calculator and computer plots can be

deceptive. Often the solution is to ﬁnd a better viewing window. In Figure 11 we

have plotted the function f (x) 5 100x and the function g (x) 5 100x 1 sin (x

)over

the interval [0, 2]. The graphs of f and g over this interval appear to be the same line

segment. Yet when we zoom in to the subinterval [1.1, 1.2], as is also shown in

Figure 11, the graphs of f and g appear to be two different line segments. Of course,

no part of the graph of g is actually a line segment. Over the interval [10, 12] the

plots of f and g once again appear virtually indistinguishable (Figure 12). When we

zoom in to the subinterval [10.1, 10.11], we can see the expected sinusoidal oscil-

lations that the plot of g has about the line y 5 100x.

m Figure 9

334 Chapter

4 Applications of the Derivative