Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

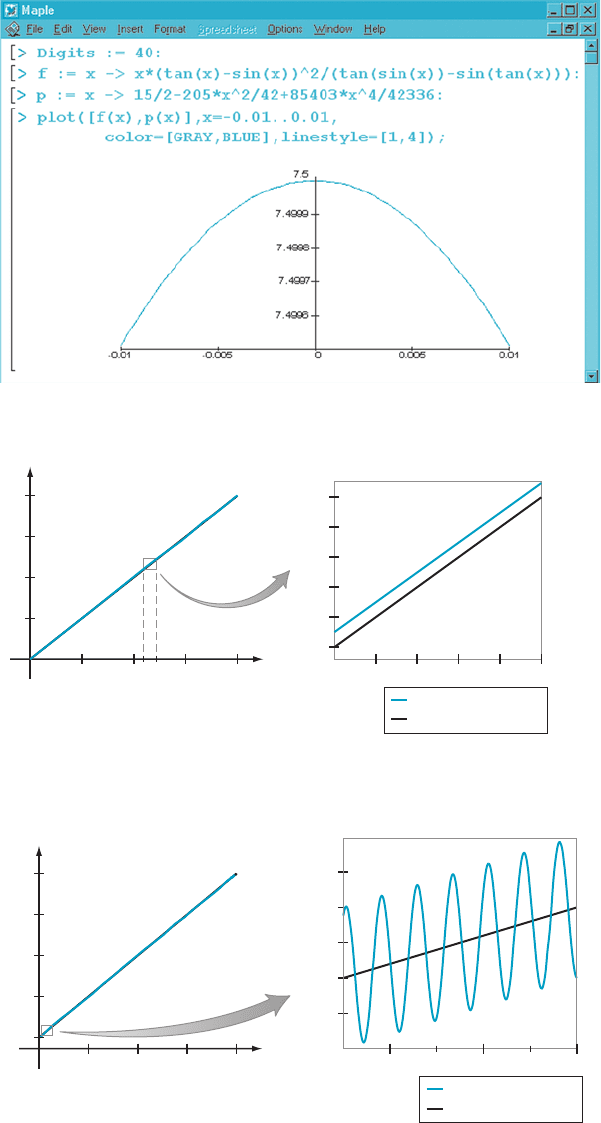
m Figure 1 0

200

150

100

0.5 1.0 1.5 2.0

110

112

114

116

118

120

1.12 1.14 1.16 1.18 1.20

g(x)  100x  sin(x

)

f (x)  100x

m Figure 11

1200

1150

1100

1050

10.5 11.0 11.5 12.0

1000

1011.5

1011.0

1010.5

1010.0

1009.5

10.102 10.106 10.110

g(x)  100x  sin(x

)

f (x)  100x

m Figure 12

4.6 Graphing Functions 335

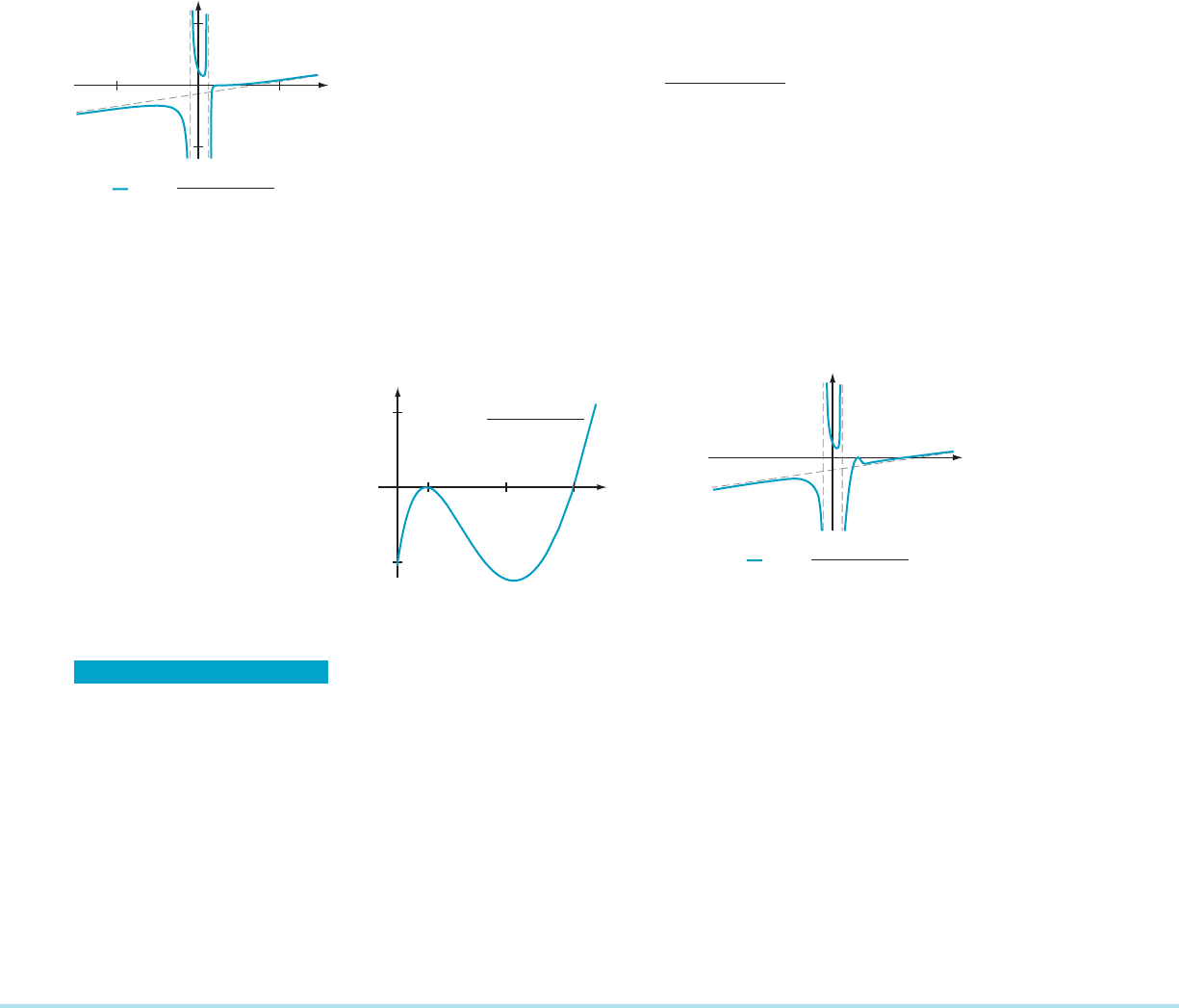
Sometimes a sketch is more useful than an accurate graph. In Figure 13 the

function

f ðxÞ5

ðx 2 2Þ

ðx 2 3Þ

ðx

2 1Þ

has been plotted in the viewing rectangle [215, 15] 3 [250, 50]. This plot reveals

many features of f : a local maximum near x 525, a local minimum near x 5 1/2,

vertical asymptotes x 521andx 5 1, and a skew-asymptote y 5 x 2 7. However,

this plot hides important information and, as a result, makes f (x) appear to be

increasing for x . 1. When we plot f over the interval [1.8, 3.2] , as in Figure 14, we

discover two local extrema, a point of inﬂection, and a second x-intercept, none of

which is visible in Figure 13. We may incorporate all the information about f into a

sketch as in Figure 15. But Figure 15 has been obtained by distorting the distance

between the two x-intercepts. There is simply no scale available that allows all

features of the graph of f to be clearly visible in one viewing window.

QUICK QUIZ

1. What are the periods of sin (x/2), sec (x), and cot (x)?

2. What is the skew-asymptote of f (x) 5 (3x

2 2x 1 5 cos (x))/x?

3. If f (x) 5 2x

/(x 2 1)

, then f

(x) 5 2x

(x 2 3)/(x 2 1)

and f

(x) 5 12x/(x 2 1)

Determine (i) the interval or intervals on which f increases, (ii) the interval

or intervals on whi ch f decreases, (iii) all local extrema, (iv) the interval or

intervals on which the graph of f is concave up, (v) the interval or intervals on

which the graph of f is concave down, (vi) all points of inﬂection, (vii) all

horizontal and vertical asymptotes, and (viii ) all skew-asymptotes.

Answers

1. 4π,2π, π 2. y 5 3x 2 2

3. (i) (2N, 1) and (3, N), (ii) (1, 3), (iii) local mini-

mum at x 5 3, (iv) (0, 1) and (1, N), (v) (2N, 0), (vi) 0, (vii) x 5 1 (vertical

asymptote), (viii) y 5 2x 1 4

f(x) 

(x  2)

(x  3)

 1

10

50

m Figure 13

2.0 2.5

0.02

0.02

f(x) 

(x  2)

(x  3)

 1

m Figure 14

f(x) 

(x  2)

(x  3)

 1

m Figure 15

EXERCISES

Problems for Practice

c Follow the outline given in this section to give a careful

sketch of the graph of each of the functions in Exercises

1224.

Your sketch should exhibit, and have labeled, all of the

following: a) local and global extrema, b) inﬂection points,

c) intervals on which function is increasing or decreasing,

d) intervals on which function is concave up or concave down,

e) horizontal and vertical asymptotes. b

336 Chapter 4 Applications of the Derivative

1. f (x) 5 x

2 3x

2 9x 1 7

2. f (x) 5 x

(x 2 8)

3. f (x) 5 (x 1 1)(x 2 2)

4. f (x) 5 x

2 6x

1 8x

5. f (x) 5 x/(x

1 4)

6. f (x) 5 (x 1 1)/(x 2 1)

7. f (x) 5 (x

1 4)/(x

2 4)

8. f (x) 5 (x 1 1)/(x 1 2)

9. f (x) 5 x

2 x

1/2

10. f (x) 5 x/(x 2 4)

11. f (x) 5 sin (x) 2 x

12. f (x) 5 cos (x) 2 sin (x)

13. f (x) 5 ( x

1/3

1 1)/x

14. f (x) 5 x

2 4/3

(x 1 2)

15. f (x) 5 x

1/3

/(x 1 3)

16. f (x) 5 ( x

2 12x)/(x

1 4)

17. f (x) 5 x (x 1 1)

1/5

18. f (x) 5 |x|/(x 1 1)

19. f (x) 5 x

1/3

(x 2 2)

20. f (x) 5

ﬃﬃﬃ

=ð

ﬃﬃﬃ

2 1Þ

21. f (x) 5

ﬃﬃﬃ

/(x 1 1)

22. f (x) 5 x 1 54/

ﬃﬃﬃ

23. f (x) 5 x

1 16/x

24. f (x) 5 1/x 2 1/x

Further Theory and Practice

c Sketch the graph of each of the functions in Exercises

25240,

exhibiting and labeling: a) all local and global

extrema; b) inﬂection points; c) intervals on which the func-

tion is increasing or decreasing; d) intervals on which the

function is concave up or concave down; e) all horizontal and

vertical asymptotes. b

25. f (x) 5 x

1/3

/(x 2 4)

26. f ðxÞ5

2=3

2 x

1=3

27. f (x) 5 x

(1 2 x

)

1/2

28. f (x) 5 x

/(x

1/3

1 8)

29. f (x) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 8x 1 18

30. f (x) 5 |x

2 9|

31. f (x) 5 (x 2 5)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

jx 1 2j

32. f (x) 5 cos

(x), 0 , x , 2π

33. f (x) 5 (x

1 x 1 1)/x

34. f (x) 5 sin (x) 1 tan (x), 2 π , x , π

35. f (x) 5 tan (x) 1 sec (x)

36. f (x) 5 |x

1/3

2 4|

37. f (x) 5 |x| (x 1 1)

38. f (x) 5 (x 1 1)/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ðx21Þ

39. f (x) 5 (13x 1 14)/(x

2 1)

40. f (x) 5 (3x 1 2)/|x

2 1|

c In Exercises 41 and 42,

follow the instructions for Exer-

cises 25240. Additionally, determine the skew-asymptote of

the given function. b

41. f (x) 5 ( x

2 4)/(2x)

42. f (x) 5 ( x

1 x

1 2)/x

43. Suppose that f : R-R is twice differentiable and f

(x) $ 1

for all x. Prove that the graph of f cannot have any hor-

izontal asymptotes.

44. A graph is called symmetric with respect to the y-axis if

(2x, y) lies on the graph whenever (x, y) lies on the graph.

We test for symmetry with respect to the y axis by

replacing x with 2 x in the equation for the graph. If the

equation remains unchanged, the symmetry property

holds. Explain the reasoning behind this test. A graph is

called symmetric with respect to the origin if (2x, 2y) lies

on the graph whenever (x, y) lies on the graph. We test for

symmetry with respect to the origin by replacing x with

2x and y with 2y in the equation for the graph. If the

equation remains unchanged, the symmetry property

holds. Explain the reasoning behind this test. Test each of

the following for symmetry in the y-axis and symmetry

in the origin. Give a sketch of each graph.

a. 9y

2 x

5 36

b. x

1 y

5 4

c. x

2 4y

5 16

d. x 1 sin (y) 5 3y

Calculator/Computer Exercises

c Follow the outline given in this section to give a careful

sketch of the graph of each of the functions in Exercises

45254.

Your sketch should exhibit, and have labeled, all of

the following: (i) all local and global extrema, (ii) inﬂection

points, (iii) intervals on which function is increasing or

decreasing, (iv) intervals on which function is concave up or

concave down, (v) all horizontal, vertical, and skew-

asymptotes. b

45. f (x) 5 x

1 6x

1 x

1 x 2 4

46. f (x) 5 x

1 x

1 2x

47. f (x) 5 x

1 x

2 5x

1 6x 1 6

48. f ðxÞ5

ðx 2 1Þðx 2 4Þ

ðx 2 3Þðx 2 2Þ

49. f ðxÞ5 x

1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 x

50. f ðxÞ5

ðx 2 3Þ

ðx 2 4Þ

ðx 2 3Þðx 2 2Þ

51. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 2 x

1 1

52. f ðxÞ5

1 x 1 1

1 4x 1 5

53. f ðxÞ5

1 20x 1 15

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

16 1 x

54. f ðxÞ5

2 x 1 2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2x

1 2

4.6 Graphing Functions 337

55. Plot

f ðxÞ5

2 1

1 1

and gðxÞ5

2 102x

1 100

2 99x

2 100

over the intervals [0, 8.5] and [8.5, 9.9]. Explain why the

graphs over the ﬁrst interval are so similar and why

the graphs over the second interval become very different.

56. Plot the function

f ðxÞ5

1 10000x

1 x 1 10000

over the interval [215, 15]. What appears to be the

asymptote for f ? Analyze f for asymptotes and plot f in a

window that better illustrates its asymptote.

57. Plot f (x) 5 12x

2 2565x

1 146200x

1 1forx 2 I 5

[0, 300]. Plot f

and f

for x 2 I.Isf increasing on I ?Isf

. 0

on I? Is the graph of f concave up on I ?Isf

. 0onI ?

4.7 l’Ho

pital’s Rule

Consider the limit

lim

x-c

f ðxÞ

gðxÞ

: ð4:7:1Þ

If lim

x-c

f ðxÞ exists and if lim

x-c

gðxÞ exists and is not zero, then the limit

(4.7.1) is straightforward to evaluate (Section 2.2). However, the situation is more

complicated when lim

x-c

gðxÞ50: For example, if f ðxÞ5 sinðxÞ ; gðxÞ5 x ,andc 5 0,

then we know that limit (4.7.1) exists and equals 1 (Section 2.2). However, if f (x) 5 x

and g (x) 5 x

, then the limit of the quotient as x-0 does not exist.

In this section we learn a rule for evaluating limits of the type (4.7.1) when

either lim

x-c

f ðxÞ5 lim

x-c

gðxÞ5 0 or lim

x-c

f ðxÞ5 lim

x-c

gðxÞ56N: In these

cases, when the limits of the num erator and den ominator of (4.7.1) are evaluated

independently, the quotient takes the form

: Such forms of the limit

are called indeterminate forms because the symbols

and

have no meaning.

The limit might actually exist and be ﬁnite or might not exist. One cannot analyze

such a form simply by evaluating the limits of the numerator and denominator and

forming their quotient.

l’Ho

pital’s Rule for the

Indeterminate Form

Suppose that f

and g

are continuous at c and f (c) 5 g (c) 5 0. Provided there are

no divisions by zero, we have

lim

x-c

f ðxÞ

gðxÞ

5 lim

x-c

f ðxÞ2 f ðcÞ

gðxÞ2 gðcÞ

5 lim

x-c

f ðxÞ2 f ðcÞ

x 2 c

gðxÞ2 gðcÞ

x 2 c

lim

x-c

f ðxÞ2 f ðcÞ

x 2 c

lim

x-c

gðxÞ2 gðcÞ

x 2 c

ðcÞ

and

lim

x-c

ðxÞ

lim

x-c

ðxÞ

lim

x-c

ðxÞ

ðcÞ

Therefore

lim

x-c

f ðxÞ

gðxÞ

5 lim

x-c

ðxÞ

338 Chapter 4 Applications of the Derivative

This observation suggests the following procedure for calculating the limit (4.7.1):

THEOREM 1

(l’Hoˆ pital’s Rule) Let f and g be differentiable functions on an

interval (a, c) to the left of c and on an interval (c, b) to the right of c.If

lim

x-c

f ðxÞ5 lim

x-c

gðxÞ5 0

then

lim

x-c

f ðxÞ

gðxÞ

5 lim

x-c

ðxÞ

provided that the limit on the right exists as a ﬁnite or inﬁnite limi t.

A proof of l’Ho

pital’s Rule is outlined in Exercises 8688. Meanwhile, let’s see

some examples in which it is used.

⁄ EX

AMPLE 1 Evaluate

lim

x-1

lnðxÞ

2 1

Solution We

ﬁrst notice that both the numerator and denominator have limit 0 as

x-1. Thus the quotient is indeterminate at 1 and of the form

: L’Ho

pital’s Rule

applies and the limit equals

lim

x-1

lnðxÞ

2 1

5 lim

x-1

lnðxÞ

ðx

2 1Þ

;

provided this last limit exists. We calculate

lim

x-1

lnðxÞ

ðx

2 1Þ

5 lim

x-1

1=x

The requested limit has value 1/2.

INSIGHT

When we apply l’Ho

pital’s Rule to a limit of type (4.7.1) as in Example 1,

we calculate the derivative of the numerator f and the derivative of the denominator g.

We do not calculate the derivative of the quotient f/g.

⁄ EXAMPLE 2 Evaluate the limit

lim

x-0

x 2 sinðxÞ

Solution As x-0

both numerator and denominator tend to zero, so the quotient is

indeterminate at 0 of the form 0/0. Thus l’Ho

pital’s Rule applies. Our limit equals

4.7 l’Ho

pital’s Rule 339

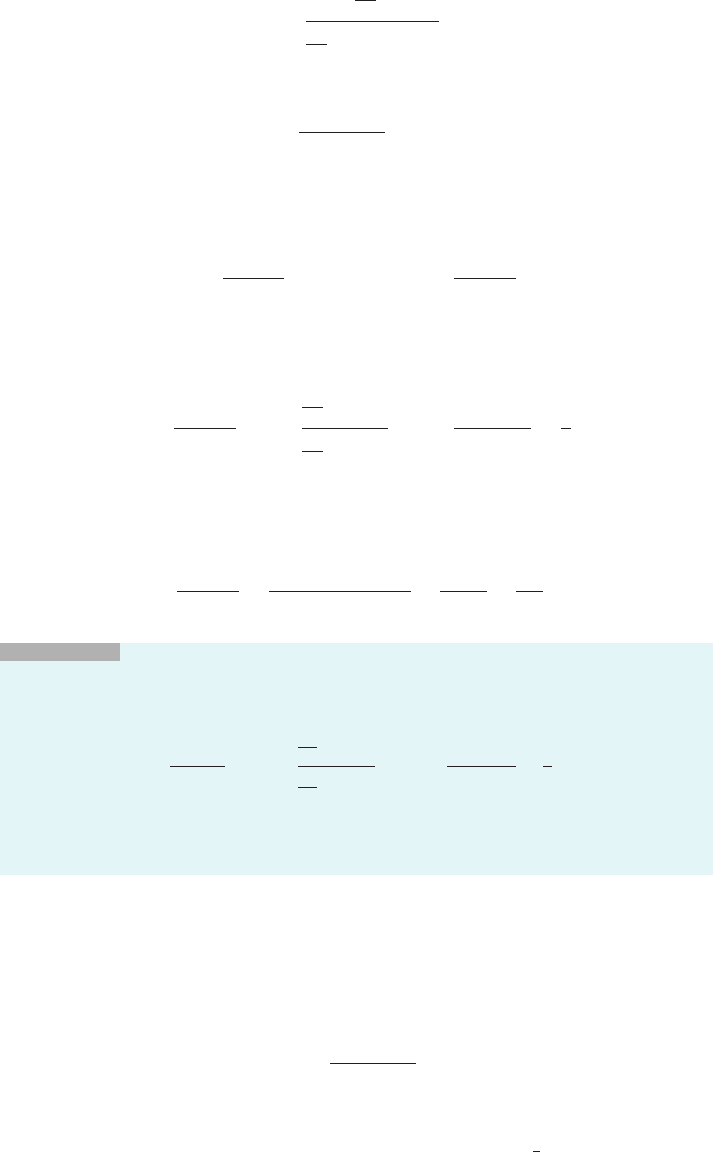
lim

x-0



x 2 sinðxÞ



;

provided that this last limit exists. It equals

lim

x-0

1 2 cos ðxÞ

51N :

We conclude that the original limit equals 1N.

⁄ EXAMPLE 3 Calculate

lim

x-0

sinð3xÞ

sinð2xÞ

and lim

x-π=6

sinð3xÞ

sinð2xÞ

Solution With

the ﬁrst limit we may proceed as in Examples 1 and 2. We

summarize the calculations:

lim

x-0

sinð3xÞ

sinð2xÞ

5 lim

x-0

sinð3xÞ

sinð2xÞ

5 lim

x-0

3 cosð3xÞ

2 cosð2xÞ

For the second limit, we calc ulate lim

x-π=6

sinð3xÞ5 sinðπ=2Þ5 1 and

lim

x-π=6

sinð2xÞ5 sinðπ=3Þ5

ﬃﬃﬃ

=2. Ther efore l’Ho

pital’s Rule does not apply.

However, we do not need it because

lim

x-π=6

sinð3xÞ

sinð2xÞ

lim

x-π=6

sinð3xÞ

lim

x-π=6

sinð2xÞ

ﬃﬃﬃ

: ¥

INSIGHT

It is tempting to apply l’Ho

pital’s Rule to any limit that is written as a

quotient. However, l’Ho

pital’s Rule is valid only when its hypotheses are satisﬁed. If we had

applied l’Ho

pital’s Rule to the second limit in Example 3, then we would have obtained

lim

x-π=6

sinð3xÞ

sinð2xÞ

5 lim

x-π=6

sinð3xÞ

sinð2xÞ

5 lim

x-π=6

3cosð3xÞ

2cosð2xÞ

5 0;

which is wrong. The error here is that we did not check that the numerator and denominator

both have limit zero; in other words, we did not check that the quotient is indeterminate.

When we apply l’Ho

pital’s Rule we may end up with another indeterminate

form. Sometimes we need to apply l’Ho

pital’s Rule two or more times to evaluate a

limit:

⁄ EX

AMPLE 4 Evaluate the limit

lim

x-π

1 1 cosðxÞ

ðx 2 πÞ

Solution Notice

that both the numerator and denominator tend to zero as x-π.

Therefore the quotient is indeterminate at π of the form

: So we may apply

l’Ho

pital’s Rule to evaluate the limit. It equals

340 Chapter 4 Applications of the Derivative

lim

x-π

2sinðxÞ

2ðx 2 πÞ

;

provided that this limit exists. However both the numerator and denominator of

this last expression tend to zero as x-π, so we apply l’Ho

pital’s Rule again. The

last limit equals

lim

x-π

2cosðxÞ

;

provided that this latest limit exists. But it clearly does exist, and it equals 1/2. We

conclude that

lim

x-π

1 1 cos ðxÞ

ðx 2 πÞ

: ¥

l’Ho

pital’s Rule for the

Indeterminate Form

There is another version of l’Ho

pital’s Rule, which can be used for the inde-

terminate form

(and the related forms

and

THEOREM 2

Let f (x) and g (x) be differentiable functions on an interval (a, c)

to the left of c and on an interval (c, b) to the right of c. If lim

x-c

f ðxÞ and

lim

x-c

gðxÞ both exist and equal 1N or 2N (they may have the same sign or

different signs) then

lim

x-c

f ðxÞ

gðxÞ

5 lim

x-c

ðxÞ

;

provided this last limit exists either as a ﬁnite or inﬁnite limit.

⁄ EX

AMPLE 5 Evaluate

lim

x-0

4 1 1=x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1 9=x

Solution In

this example, we set f ðxÞ5 4 1 1=x

and gðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1 9=x

. Because

lim

x-0

f ðxÞ5 N and lim

x-0

gðxÞ5 N; we may apply Theorem 2. We obtain

lim

x-0

4 1 1=x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1 9=x

5 lim

x-0

ð4 1 1=x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 1 9=x

5 lim

x-0

22=x

2 18=ðx

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 9

218

lim

x-0

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 9

ﬃﬃﬃ

: ¥

4.7 l’Ho

pital’s Rule 341

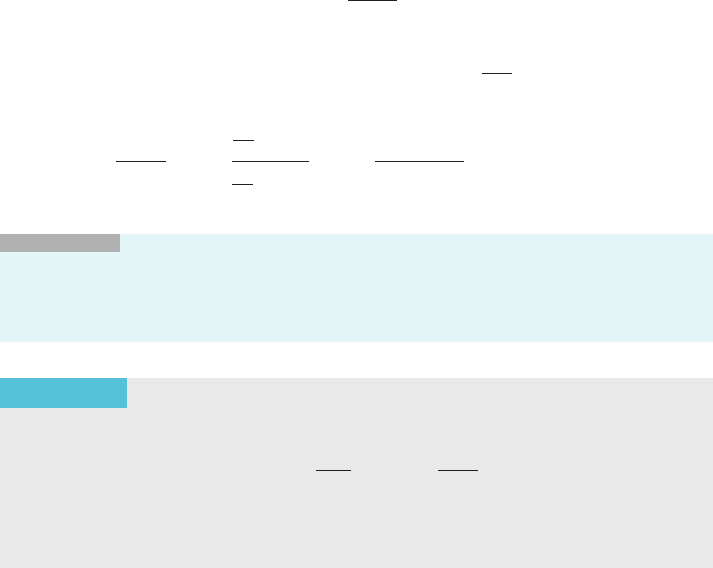
The Indeterminate

Form 0  N

L’Ho

pital’s Rule applies only to quotients. Nevertheless, we may be able to rewrite

a non-quotient as a quotient so that l’Ho

pital’s Rule may be applied . The inde-

terminate form 0:N is often handled in this way. The next exampl e illustrates the

technique.

⁄ EX

AMPLE 6 Evaluate the limit lim

x-0

 lnðx

Þ:

Solution We

may rewrite the orgina l limit as

lim

x-0

lnðx

1=x

Notice that the numerator tends to 2N and the denominator tends to 1N as x-0.

Thus the quotient is indeterminate at 0 of the form

: Theorem 2 therefore

applies. Accordingly, we have

lim

x-0

lnðx

1=x

5 lim

x-0

lnðx

ð1=x

5 lim

x-0

ð1=x

Þð2xÞ

2 2x

52lim

x-0

5 0: ¥

INSIGHT

In Example 6, a formal limit computation results in lim

x-0

 lnðx

Þ5

0 ð2NÞ: Although the expressions 0 N and 0 (2N) are also called indeterminate

forms, l’Ho

pital’s Rule does not directly address them. An algebraic manipulation is

required to rewrite the limit in a way that is appropriate for l’Ho

pital’s Rule.

l’Ho

pital’s Rule for

Limits at N

THEOREM 3

Let f and g be differentiable functions. If lim

x-1N

f ðxÞ5

lim

x-1N

gðxÞ5 0; or if lim

x-1N

f ðxÞ56N and lim

x-1N

gðxÞ56N; then

lim

x-1N

f ðxÞ

gðxÞ

5 lim

x- 1N

ðxÞ

provided that this last limit exists either as a ﬁnite or inﬁnite limit. The same

result holds for the limit as x-2N:

⁄ EX

AMPLE 7 Evaluate lim

x-1N

Solution We

ﬁrst notice that both the numerator and the denominator tend to 1N

as x- 1N. Thus the quotient is indeterminate at 1N of the form 1N/1N.

Therefore Theorem 3 applies and our limit equals lim

x-1N

2x=e

: Again the

numerator and denominator tend to 1N as x- 1N so we again ap ply Theorem 3.

The limit equals lim

x-1N

2=e

5 0: We conclude that lim

x-1N

5 0: ¥

The Indeterminate

Form 0

If x is any positive number, then x

5 1. It follows that lim

x-0

5 1, which may

suggest the (false) conclusion that the form 0

is 1. We can see that the situation is

not so straightforward by observing that lim

x-0

5 lim

x-0

0 5 0, which may

suggest the (equally false) conclusion that the form 0

is 0. In fact , 0

is inde-

terminate and must be analyzed carefully. The usual technique is to ﬁrst apply the

logarithm, which reduces an expression involving exponenti als to one involving a

product or a quotient. A further algebraic manipulation may be required to rewrite

the limit in a way that is appropriate for l’Ho

pital’s Rule.

342 Chapter 4 Applications of the Derivative

⁄ EXAMPLE 8 Evaluate lim

x-0

Solution We

study the limit of f (x) 5 x

by considering ln ( f (x)) 5 x ln (x). We

rewrite this as

lim

x-0



f ðxÞ



5 lim

x-0

lnðxÞ

1=x

The numerator tends to 2N and the denominator tends to 1N, so the quotient is

indeterminate of the form

1 N

: L’Ho

pital’s Rule therefore applies. We calculate

lim

x-0

lnðxÞ

1=x

5 lim

x-0

lnðxÞ

ð1=xÞ

5 lim

x-0

1=x

2 1=x

5 lim

x-0

ð2xÞ5 0:

Now the only way that ln ( f (x)) can tend to zero is if f (x) 5 x

tends to 1. We

conclude that lim

x-0

5 1. ¥

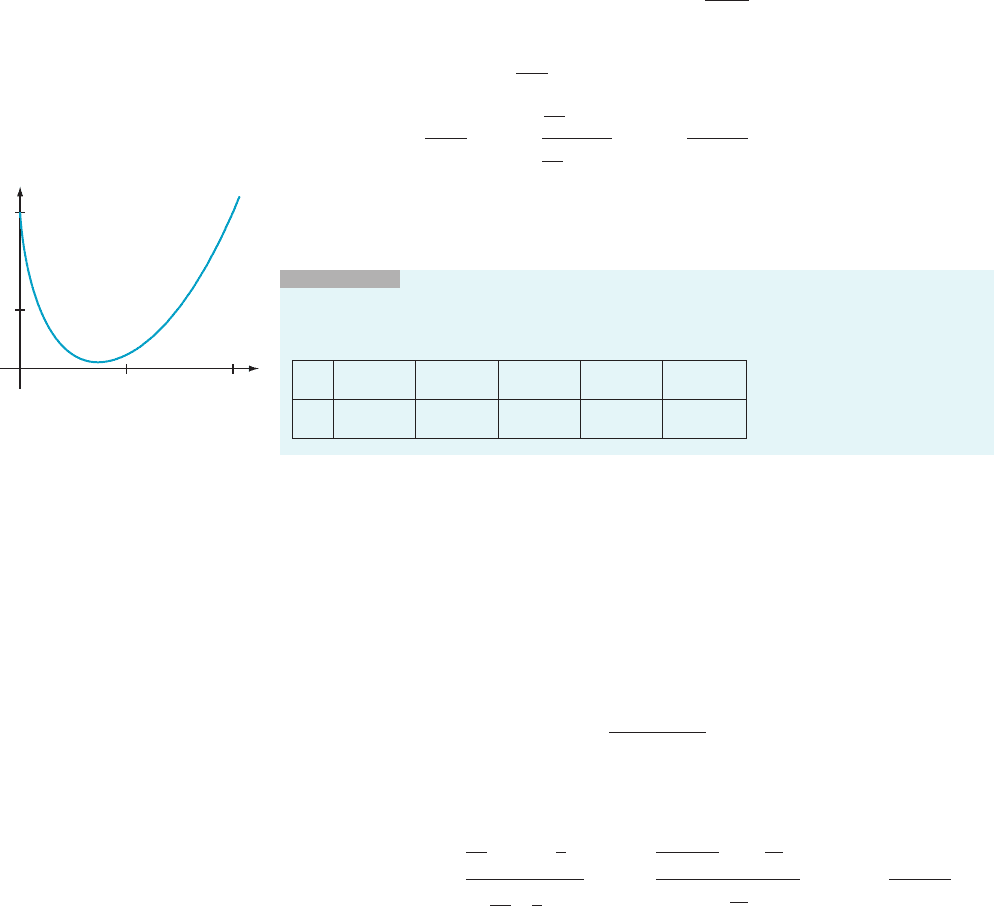
INSIGHT

The limit in Example 8 is not obvious. A plot of x

for 0 , x . 1 (Figure1)

provides us with visual evidence that our calculation is correct. Moreover, numerical

evidence also supports our conclusion:

x 0.1 0.01 0.001 0.0001 0.00001

0.7943 0.9550 0.9931 0.9991 0.9999

The Indeterminate

Form 1

Because 1

5 1 for any real number x, it might seem that the indeterminate form 1

should equal 1. The next example will prove otherwise. As with the form 0

, the

technique for handling 1

is to ﬁrst apply the logarithm.

⁄ EX

AMPLE 9 Use l’Ho

pital’s Rule to evaluate lim

x-N

ð1 1 3= x Þ

Solution Let f ðxÞ5 ð1 1 3=xÞ

and consider ln ( f (x)) 5 lnðð1 1 3=xÞ

Þ5

x  ln ð1 1 3=xÞ. This expression is indeterminate of the form N0.

We rewrite it as

lim

x-N

lnð1 1 3=xÞ

1=x

;

so that both the numerator and denominator tend to 0. In this form l’Ho

pital’s Rule

applies and we have

lim

x-N

lnðf ðxÞÞ5 lim

x-N



1 1







5 lim

x-N

1 1 3=x







5 3 lim

x-N

1 1 3=x

5 3:

Because the only way ln ( f (x)) can tend to 3 is if f (x) tends to e

, we conclude that

lim

x-N

ð1 1 3=x Þ

5 e

, which agrees with formula (2.6.13). ¥

The Indeterminate

Form N

As with the forms 0

and 1

, the technique for handlin g N

is to ﬁrst apply the

logarithm.

1.0

10.5

y  x

0.8

m Figure 1

4.7 l’Ho

pit

al’s Rule 343

⁄ EXAMPLE 10 Calculate lim

x-N

1=x

Solution We

study the limit of f (x) 5 x

1/x

by considering ln ( f (x)) 5 ln (x)/x, which

gives us an indeterminate form that is suitable for l’Ho

pital’s Rule. We have

lim

x-N

lnðf ðxÞÞ5 lim

x-N

lnðxÞ

5 lim

x-N

lnðxÞ

5 lim

x-N

1=x

5 0:

Now the only way that ln ( f (x )) can tend to zero as x tends to inﬁnity is if f (x) 5 x

1/x

tends to 1. We conclude that lim

x-N

1=x

5 1. ¥

Putting Terms over a

Common Denominator

Many times, a simple algebraic manipulation will put a limit into a form that can be

studied using l’Ho

pital’s Rule. The next example illustrates this idea.

⁄ EX

AMPLE 11 Evalu ate the limit

lim

x-0



sinðxÞ



Solution We

put the fractions over a common denominator to rewrite our limit as

lim

x-0



x 2 sinðxÞ

x  sinðxÞ



Both numerator and denominator vanish as x-0. Thus the quotient has inde-

terminate form 0/0. By l’Ho

pital’s rule, the limit is therefore equal to

lim

x-0



x 2 sinðxÞ

x  sinðxÞ



5 lim

x-0



x 2 sinðxÞ





x sinðxÞ



5 lim

x-0

1 2 cos ðxÞ

sinðxÞ1 xcosðxÞ

This quotient is still indeterminate; we apply l’Ho

pital’s rule again to obtain

lim

x-0



x 2 sinðxÞ

x sinðxÞ



5 lim

x-0



1 2 cosðxÞ





sinðxÞ1 x cosðxÞ



5 lim

x-0

sinðxÞ

2 cosðxÞ2 xsinðxÞ

2 2 0

5 0: ¥

⁄ EX

AMPLE 12 Calcu late lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

2 xÞ:

Solution Th

e algebraic technique with which we treat this difference is known as

conjugation. We have previously used this method in Example 4 of Section 2.2. In this

technique, we multiply and divide

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

2 x by its conjugate,

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

1 x. Thus

lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

2 xÞ5 lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

2 xÞð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

1 xÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

1 x

5 lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

1 x

This limit has indeterminate formN/N. However, repeated applications of l’Ho

pital’s

Rule do not lead to a simpler limit, as you may wish to verify. Instead, we calculate as

follows:

lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

1 x

5 lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ð1 1 6=xÞ

1 x

5 lim

x- 1N

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 6=x

1 x

5 lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 6=x

1 x

5 lim

x- 1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 6=x

1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 0

1 1

5 3:

344 Chapter 4 Applications of the Derivative