Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

(In this calculation, notice that the expression |x| simpliﬁes to x because x assumes

positive values as x- 1N.)

INSIGHT

In each of Examples 11 and 12, the original difference leads to the

indeterminate form N2N. However, even though the two terms of the difference

individually have inﬁnite limits, their difference results in a subtle cancellation that yields

a ﬁnite limit.

b A LOOK BACK We have encountered seven types of indeterminate forms. The

two basic indeterminate forms

and

can be handled directly with l’Ho

pital’s

Rule. The indeterminate form 0 Nis generally converted to one of the basic forms

by placing the reciprocal of one of the factors in the denominator. That is, 0 N is

treated as

1=0

1=N

Some algebraic manipulation is necessary before l’Ho

pital’s Rule can be applied to

the indeterminate form N2N. The three indeterminate forms that involve expo-

nents, namely 0

, and N

, are converted to the indeterminate form 0 N by

applying the logarithm.

QUICK QUIZ

1. If lim

x-c

f ðxÞ5 lim

x-c

gðxÞ5 α, then what must α be to apply l’Ho

pital’s Rule to

the limit lim

x-c

ðf ðxÞ=gðxÞÞ?

2. Evaluate lim

x-0

tanð3xÞ=tanð2x Þ.

3. For which indeterminate forms is it helpful to ﬁrst apply the logarithm?

4. Evaluate lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 12x

2 xÞ:

Answers

1. α 5 0, α 52N,o

rα 51N 2. 3/2 3. 0

, and N

4. 6

EXERCISES

Problems for Practice

c In each of Exercises 1216, use l’Ho

pital’s Rule to ﬁnd the

limit, if it exists. b

1. lim

x-0

ð1 2 e

Þ=x

2. lim

x-1N

lnðxÞ=

ﬃﬃﬃ

3. lim

x-5

lnðx=5Þ

x 2 5

4. lim

x-0

x 1 sinð5xÞ

x 2 3 sinð4xÞ

5. lim

x-π=2

lnðsinðxÞÞ

ðπ 2 2xÞ

6. lim

x-0

cosðxÞ2 1

2 1

7. lim

x-21

cosðx 1 1Þ2 1

1 x

2 x 2 1

8. lim

x-0

2 e

9. lim

x-0

2 e

10. lim

x-21

x 1 x

lnð2 1 xÞ

11. lim

x-1

lnðxÞ

x 2

ﬃﬃﬃ

12. lim

x-0

sin

ð3xÞ

1 2 cosð4xÞ

13. lim

x-1N

sinð3=xÞ

sinð9=xÞ

4.7 l’Ho

pital’s Rule 345

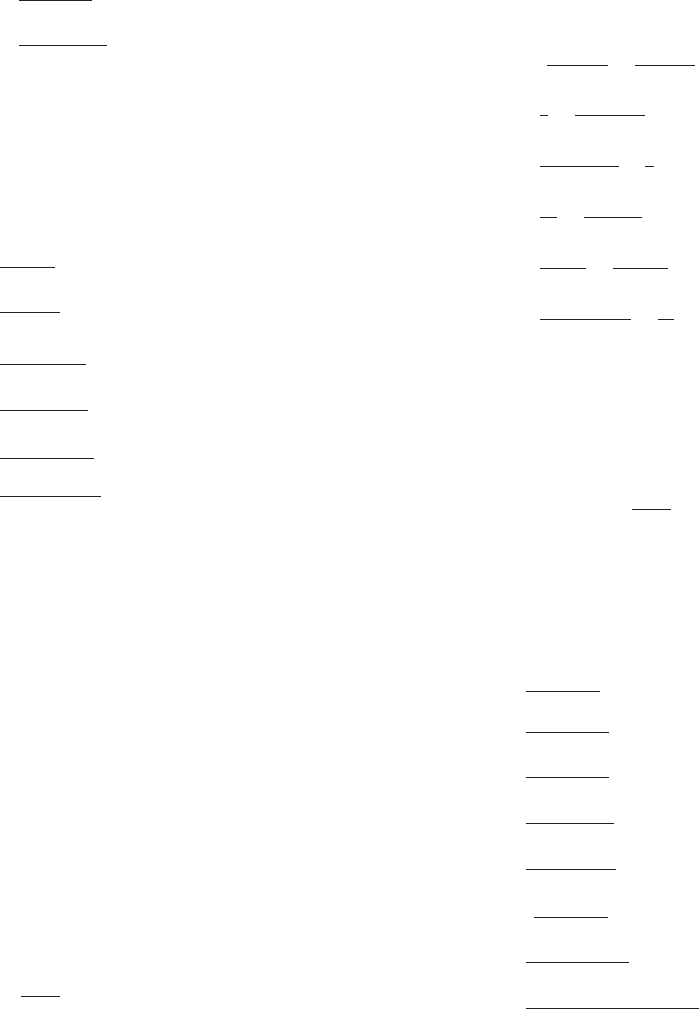
14. lim

x-1N

sin

ð2=xÞ

3=x

15. lim

x-2N

ln ð1 1 1=xÞ

sinð1=xÞ

16. lim

x-π=2

tanð2xÞ=cot ðxÞ

c In each of Exercises 17224,

apply l’Ho

pital’s Rule

repeatedly (when needed) to evaluate the given limit, if it

exists. b

17. lim

x-N

18. lim

x-N

19. lim

x-0

sin

ðxÞ

20. lim

x-1

ðx 2 1Þ

ðxÞ

21. lim

x-1

ðx 2 1Þ

cos

ðπx=2Þ

22. lim

x-0

1 2 cosð4xÞ

sin

ðxÞ

23. lim

x-0

sinð2xÞ2 2x

24. lim

x-0

2 e

2 2x

sinðx

c In each Exercises 25232,

use an algebraic manipulation to

put the limit in a form which can be treated using l’Ho

pital’s

Rule; then evaluate the limit. b

25. lim

x-1N

x  e

22x

26. lim

x-0

ðe

2 e

Þx

27. lim

x-N

lnðxÞ

28. lim

x-1N

lnðxÞ

29. lim

x-1

ðx 2 1Þ

lnðxÞ

30. lim

x-0

sinðxÞcotð3xÞ

31. lim

x-22

ðx 1 2Þtanðπx=4Þ

32. lim

x-π

tanðx=2Þ sinð3xÞ

c In each of Exercises 33240,

use the logarithm to reduce

the given limit to one that can be handled with l’Ho

pital’s

Rule. b

33. lim

x-0

ﬃﬃ

34. lim

x-0

ðxÞ

35. lim

x-N



x 2 5



36. lim

x-1N



x  lnðxÞ



21=x

37. lim

x-1N

1=x

38. lim

x-21

ð2 1 xÞ

lnðx11Þ

39. lim

x-1N

ﬃﬃ

40. lim

x-2N

ðx

ðe

c In each of Exercises 41246, put the fractions over a

common denominator and use l’Ho

pital’s Rule to evaluate

the limit, if it exists. b

41. lim

x-N



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 3



42. lim

x-0



ln ðx 1 1Þ



43. lim

x-0



1 2 cosðxÞ



44. lim

x-0



3 sinðxÞ



45. lim

x-0



sinðxÞ

sinð2xÞ



46. lim

x-0



1 e

2 2



c In each of Exercises 47252,

use an algebraic manipulation

to reduce the limit to one that can be treated with l’Ho

pital’s

Rule. b

47. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4x 2 5

2 2

ﬃﬃﬃ

48. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

2 xÞ

49. lim

x-2N

ðx 1 1Þln



x 1 1



50. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

51. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 e

52. lim

x-1N



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 4x

2 ðx

1 1Þ



c In Exercises 53260,

calculate the given limit. b

53. lim

x-0

arctanðxÞ

54. lim

x-0

arcsinð3xÞ

arctanð2xÞ

55. lim

x-0

sinhðxÞ

expðxÞ2 1

56. lim

x-0

coshðxÞ2 1

sinhðxÞ

57. lim

x-0

cosh ðxÞ2 1

sinh

ðxÞ

58. lim

x-N

tanhð xÞ

arctanðxÞ

59. lim

x-0

arcsinðxÞ2 x

arctanðxÞ2 x

60. lim

x-0

arcsinh ðxÞ2 arcsinðxÞ

c In Exercises 61264, use the logarithm to reduce the

indeterminate form 1

to one that can be handled with

l’Ho

pital’s Rule. b

61. lim

x-0

ðcos ð2xÞÞ

1=x

62. lim

x-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 1=x

346 Chapter 4 Applications of the Derivative

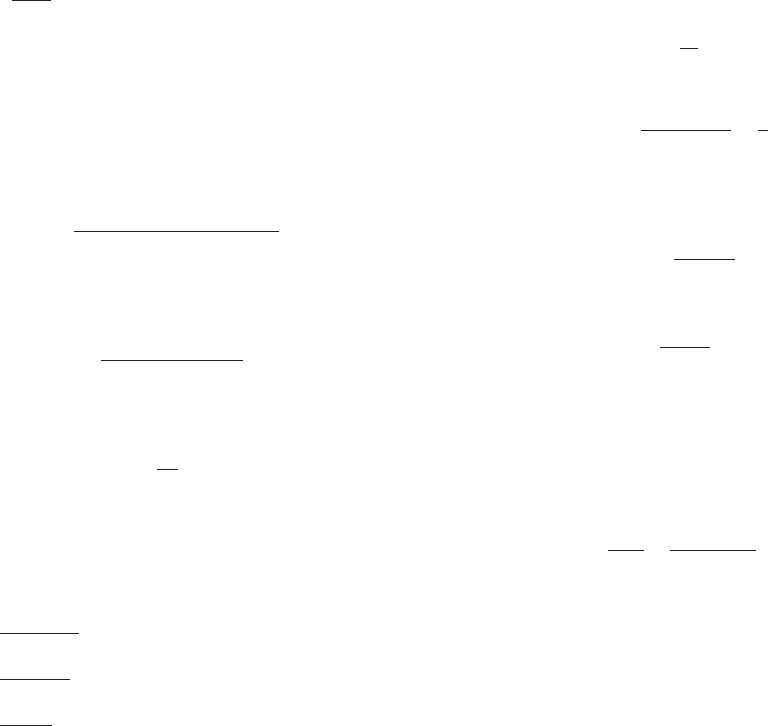
63. lim

x-N



5 1 x

2 1 x



64. lim

x-0



11 sinðxÞ



cscðxÞ

Further Theory and Practice

65. Use l’Ho

pital’s Rule to check that lim

h-0

ð1 1 hÞ

1=h

5 e:

Now calculate lim

h-0

ð1 1 hxÞ

1=h

for any ﬁxed x.

66. Use l’Ho

pital’s Rule to calculate

lim

h-0

f ðx 1 hÞ2 2f ðxÞ1 f ðx 2 hÞ

for a function f that is twice continuously differentiable at x.

67. Let a and b be constants with b 6¼1. Use l’Ho

pital’s Rule

to calculate

lim

x-0

a sinðxÞ2 sinðaxÞ

tanðbxÞ2 b tanð xÞ

68. For any real number k and any positive number a prove

that

lim

x- 1N

5 0:

c In each of Exercises 69276, use l’Ho

pital’s

Rule to eval-

uate the one-sided limit. b

69. lim

x-ðπ=2Þ

ðx 2 π=2ÞcotðxÞ

70. lim

x-π

ðx 2 πÞtanðx=2Þ

71. lim

x-0

ln ð1 1 xÞ

ln ð1 1 3xÞ

72. lim

x-0

sinðxÞ

ln ð1 1 xÞ

73. lim

x-0

2lnðxÞ

ln ð2xÞ

74. lim

x-0

lnð1 1 xÞln ðxÞ

75. lim

x-0

21=ln ðxÞ

76. lim

x-0

5=ln ð2xÞ

c In each of Exercises 77282, a function f with domain either

I 5 (2N, N)orI 5 (0,N) is given. Sketch the graph of f. (The

set C of critical points of f and the set I of inﬂection points of

f are provided in some cases.) Use l’Ho

pital’s Rule to deter-

mine the horizontal asymptote of the graph. If I 5 (0, N), use

l’Ho

pital’s Rule to determine lim

x-0

f ðxÞ: b

77. f (x) 5 x/e

; I 5 (2N, N)

78. f (x) 5 x

; I 5 (2N, N)

79. f (x) 5 e

/(e

1 x); I 5 (2N, N); I 5 {2.269 ...}

80. f (x) 5 ln (x)/x; I 5 (0, N)

81. f (x) 5 x ln (x)/(1 1 x

); I 5 (0, N); C 5 {0.301..., 3.319...};

I 5 {0.720..., 5.486...}

82. f (x) 5 ln (x)/(1/x 1 e

x21

); I 5 (0,N); C 5 {0.730 ...}; I 5

{1.646 . . . }

83. Suppose that r is a constant greater than 1. Let α be any

constant. Show that

lim

x-N

5 0:

Deduce that

lim

x-N

a  r

1 pðxÞ

b  r

1 qðxÞ

for any polynomials p (x) and q (x) and any constants a

and b with b 6¼0.

84. Evaluate

lim

x-N

ðx11Þ=x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

85. For any constants α and β with β . 0, show that

lim

x-N

ln ðxÞ

5 0:

86. Cauchy’s Mean Value Theorem states the following: If

f (x) and g (x) are functions that are continuous on the

closed interval [a, b] and differentiable on the open

interval (a, b), then there is a point ξ 2 (a, b) such that

ðgðbÞgðaÞÞ f

ðξÞ¼ðf ðbÞf ðaÞÞ g

ðξÞ. Notice that, if

both g(a) 6¼g(b) and g

(ξ) 6¼0, then

ðξÞ

f ðbÞ2 f ðaÞ

gðbÞ2 gðaÞ

Complete the following outline to obtain a proof of

Cauchy’s Mean Value Theorem

a. Let rðxÞ5



f ðbÞ2 f ðaÞ



gðxÞ2 gðaÞ





f ðxÞ2 f ðaÞ



gðbÞ2 f ðaÞ



Check that r (a) 5 r (b).

b. Apply Rolle’s Theorem to the function r on the interval

[a, b] to conclude that there is a point ξ 2(a, b)such

that r

(ξ) 5 0.

c. Rewrite the conclusion of (b) to obtain the conclusion

of Cauchy’s Mean Value Theorem.

87. Write the equation of the line through the points (g(a),

f (a)) and (g(b), f (b)). If P 5 (x, y) is a point in the plane

then calculate the vertical distance from P to this line.

Now give a geometric interpretation of the function r in

Exercise 86(a). Explain the motivation of the proof of

Cauchy’s Mean Value Theorem.

88. Use Cauchy’s Mean Value Theorem to prove the ﬁrst

form of l’Ho

pital’s Rule (Theorem 1).

Calculator/Computer Exercises

c In each of Exercises 89292, investigate the given limit

numerically and graphically. b

89. lim

x-0

ð1 2 cos ðxÞÞ=sin ðxÞ

90. lim

x-0

tanð2 sinðxÞÞ=sinð2 tanðxÞÞ

4.7 l’Ho

pital’s Rule 347

91. lim

x-0

ð12sinðxÞ=xÞ

92. lim

x-0

ð1 1 tanð2xÞÞ

1=x

c In each of Exercises 93295, illustrate the assertion of

l’Ho

pital’s Rule by plotting f/g and f

in an interval cen-

tered at c . b

93. f ðxÞ5 ð 1 2 cos ðxÞÞ; gðxÞ5 x tanðxÞ; c 5 0

94. f ðxÞ5 ð 1 1 x 2 e

Þ; gðxÞ5 x sinðxÞ; c 5 0

95. f ðxÞ5 ð1 1 cosðxÞÞ; gðxÞ5 ðx 2 πÞsin ðxÞ; c 5 π

96. Example 10 shows that lim

x-0

5 1. Plot y 5 x

for

values of x that have the form 2p/q where p and q are

positive integers with q odd. Let {x

} be a sequence of

such negative rational numbers with lim

n-N

5 0. What

can be said of lim

n-N

4.8 The Newton-Raphson Method

All quadratic equations ax

1 bx 1 c 5 0 can be solved explicitly by means of the

Quadratic Formula:

x 5

2b6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 4ac

There are formulas for solving cubic and fourth degree equations as well. However,

there are no elementary formulas for solving general polynomial equations of

degree ﬁve and higher . If we turn to transcendental equations, such as

5 x 2

sinðxÞ;

then matters are even more obscure. Yet there is often a need to solve such

equations, as we will see in several applied problems.

If we settle for an approximate solution of an e quation (with, say, a speciﬁed

number of decimal places of accuracy), then calculus enables us to ﬁnd sufﬁciently

accurate solutions for many equations that come up in practice. The technique that

we will study in this section is called the Newton-Raphson Method (or sometimes

just Newton’s Method). It is one of the methods used by calculators and computer

algebra systems to solve equations.

The Geometry of the

Newton-Raphson

Method

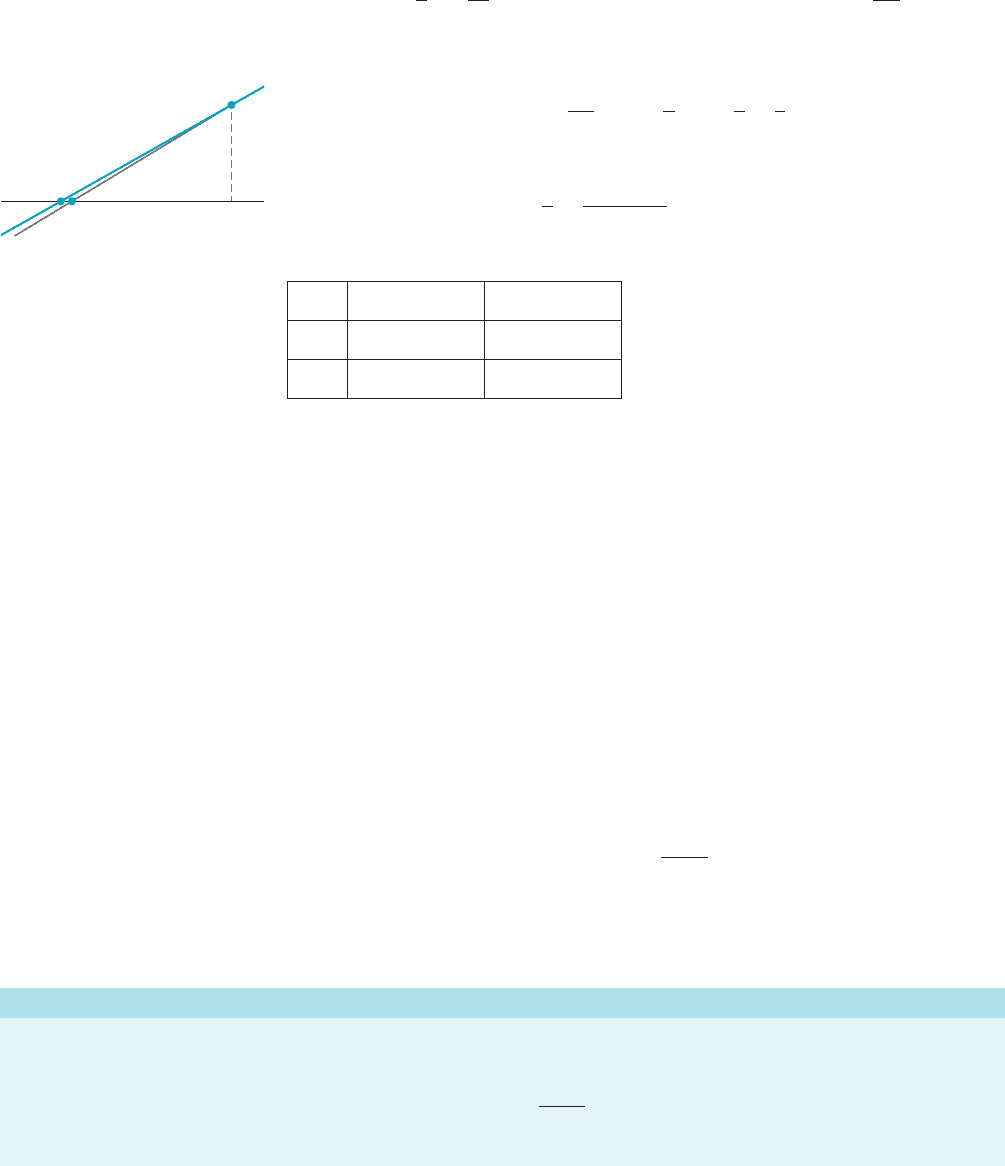
See Figure 1 for the fundamental idea behind the Newton-Raphson Method: the

graph of a differentiable function f is approximated well, near a point (x

, f (x

)), by

the tangent line ‘ at the point (x

, f (x

)). The picture suggests that, if x

is near a

point c where the graph of f crosses the x-axis, then the point x

at which ‘ intersects

the axis will be even closer. This simple observation is the basic idea of the Newton-

Raphson Method.

⁄ EX

AMPLE 1 Let P denote the point at which the graphs of y 5 cos (x) and

y 5 x cross. A very rough estimate of the x-coordinate of P is π/3. Apply the

fundamental idea behind the Newton-Raphson method to ﬁnd a better

approximation.

Solution T

he idea of the Newton-Raphson Method is to use a tangent line

approximation to improve an initial estimate of a root of an equation f (x) 5 0. We

start by casting the current problem into this form. The two curves intersect at

the value of x for which x 5 cos (x), or x 2 cos (x) 5 0. If we deﬁne f (x) 5 x 2 cos (x),

then the value c of x that we are seeking is the solution of f (x) 5 0. Let us begin

with the given estimate x

5 π/3 of c. The tangent line at (x

, f (x

)) that is, at

(π/3,π/3 2 1/2), has slope

, f(x

))

ᐉ

m Figure 1

348 Chapter

4 Applications of the Derivative







x2cosðx





x5π=3



1 1 sinðx





x5π=3

5 1 1

ﬃﬃﬃ

The point-slope equation of the tangent line is therefore

y 5



1 1

ﬃﬃﬃ



x 2







The line intersects the x-axis when y 5 0—that is, at

1=2 2 π=3

1 1

ﬃﬃﬃ

 0:75395527:

See Figure 2. Now examine the table:

x cos (x)

1.0471976 0.5

0.75395527 0.72898709

We see that x

was a rather poor estimate: the values of x and cos (x) are quite

far apart for that value of x. However, applying the idea of the Newton-Raphson

Method results in a remarkable improvement: the values of x and cos (x) diff er by

less than 0.025 at x

. ¥

What if even greater accuracy is required? In that case, we can replace x

by x

and repeat the procedure to get a better approximation x

. We keep repeating until

the desired degree of accuracy is obtained. That procedure is the Newton-Raphson

Method.

Calculating with the

Newton-Raphson

Method

To put the Newton-Raphson Method to use, we need to develop an algorithm.Ifwe

are given a differentiable function f and an initial estimate x

of a root c of f,thenthe

tangent line at (x

, f (x

)) has point-slope equation

y 5 f

ðx

Þðx 2 x

Þ1 f ðx

Þ:

Let x

be the x-intercept of this tangent line. By substituting y 5 0andx 5 x

in the

equation of the tangent line, we ﬁnd that

5 x

f ðx

ðx

; ð4:8:1Þ

provided that f

) 6¼0. If we replace x

with x

on the right side of (4.8.1), then the

resulting expression is used to deﬁne the next approximation x

, and so on. Let us

summarize what we have learned.

The Newton-Raphs on Method

If f is a differentiable function, then the (n 1 1)

estimate x

n11

for a zero of f is obtained from the n

estimate

by the formula

n11

5 x

f ðx

ðx

;

provided that f

) 6¼0.

 0.75

f(x)  x  cos(x)

 p3

m Figure 2

4.8 The Newton-Raphson Method 349

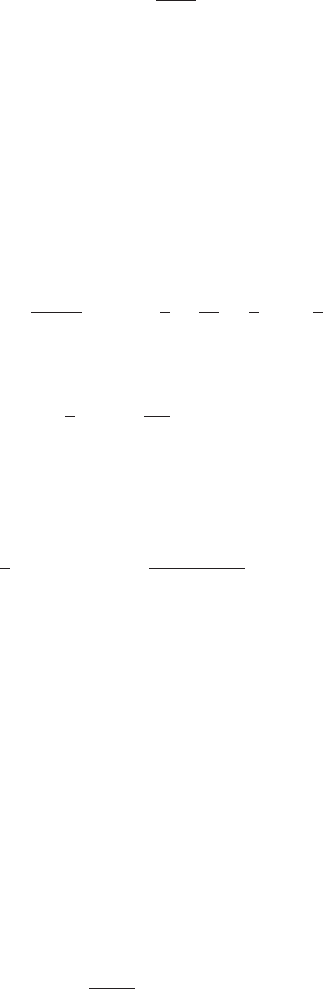
We can formulate the Newton-Raphson Method in a way that highlights its

iterative nature. Let

ΦðxÞ5 x 2

f ðxÞ

ðxÞ

: ð4:8:2Þ

Then, starting from a ﬁrst estimate x

of a root c of f (x) 5 0, we generate sub-

sequent approximations, x

, x

, . . . by the formula

j11

5 Φðx

Þ: ð4:8:3Þ

⁄ EX

AMPLE 2 Use the Newton-Raphson Method to determine

ﬃﬃﬃ

to within

an accuracy of 10

Solution Th

e problem is equivalent to ﬁnding the positive value where the function

f (x) 5 x

2 3 vanishes. We ﬁrst calculate f

(x) 5 2x and, following equation (4.8.2),

deﬁne

ΦðxÞ5 x 2



2 3



5 x 2



x 1



For a ﬁrst estimate, we take x

5 1.7. Then, according to equation (4.8.3), we get

5 Φðx

Þ5



1:7 1

1:7



5 1:73235294:

A check with a calculator reveals that x

already agrees with

ﬃﬃﬃ

to three decimal

places of accuracy. Applying the Newton-Raphson Method a second time, we

obtain our third estimate

5 Φðx

Þ5



1:73235294 1

1:73235294



5 1:7320508:

This value agrees with

ﬃﬃﬃ

to seven decimal places of accuracy, as may be veriﬁed

with a calculator.

Accuracy If we do not already know the answer in advance, or if we do not have a calculator

handy, how do we determine the accuracy of the approximation? If the Newton-

Raphson Method is to be useful in practice, then this is clearly a question that must

be answered.

Suppose that our sequence {x

} of Newton-Raphson estimates lies in an

interval on which the values of | f

(x)| are bounded by a constant C

. Suppose also

that x

and x

n 1 1

agree to k decimal places of accuracy. Then

n11

5 x

1 ε

where |ε| , 5 3 10

2(k 1 1)

. Thus

f ðx

ðx

5 x

1 ε;

f ðx

Þ52f

ðx

Þε:

350 Chapter 4 Applications of the Derivative

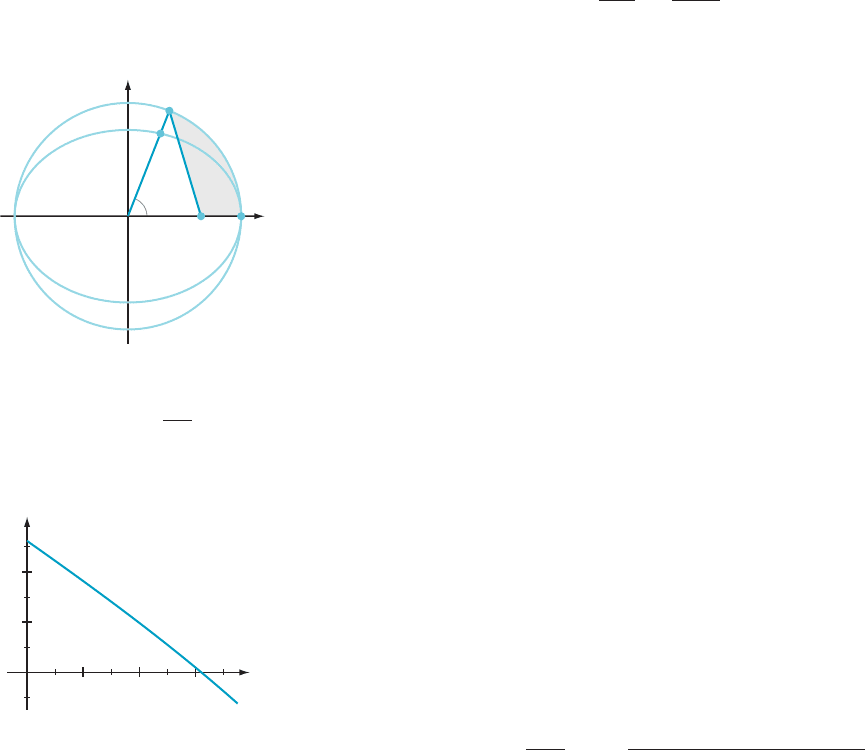
It follows that

jf ðx

Þj 5 jf

ðx

Þεj

5 jf

ðx

Þj  jεj

# C





5 3 10

2ðk11Þ



5 5  C

 10

2ðk11Þ

This inequality allows us to estimate how close f (x

) is to zero. In practice we may

just continue the iterations until two or three successive approximations are within

5 3 10

2 (k 1 1)

of each other. This is usu ally the signal that any further reﬁnement

will take place beyond the k

decimal place.

If f has a continuous second derivative, then we can say more about the rate at

which the Newton-Raphson iterates {x

} approach a root c of f. Let us denote the

absolute difference |c 2 x

|byε

.Iff

(c)andf

Raphson iterations {x

} converge to c, then it may be shown that

lim

j-N

n11



ðcÞ



: ð4:8:4Þ

We will use this result only to explain why the Newton-Raphson Method often yields

a very accurate approximation after only a few iterations. To that end, notice that the

right side of equation (4.8.4) is just a positive number—let us call it C. Equation

(4.8.4) says that ε

n11

 C ε

for large n. Thus when the Newton-Raphson Method is

successful, the (n 1 1)

error ε

n11

is approximately proportional to the square ε

the n

error. For example, if ε

is on the order of 10

,thenε

n11

will be on the order

of 10

and ε

n12

will be on the order of 10

212

. A loose rule of thumb is that, in a

successful application of the Newton-Raphson Method, the number of decimal

places of accuracy doubles with each iteration. The technical description is that the

Newton-Raphson Method is a second order process.

⁄ EX

AMPLE 3 Kepler’s equation

M 5 x 2 e sin (x)

relates the mean anomaly M and the eccentric anomaly x of a planet travelling

in an elliptic path of eccentricity e. See Figure 3. It is important in predictive

astronomy to be able to solve for x if M is given. Kepler expressed his opinion

that an exact solution for x is impossible: “ . . . if anyone would point out my mis-

take and show me the way, then he would be a g reat Apollonius in my opinion.”

Instead of ﬁnding an exact solution, ﬁnd x to four decimal places when M 5 1.0472

and e 5 0.2056 (the eccentricity of Mercury’s orbit).

Solution Let f (x) 5 1.0472 2 x 1 0.2056 sin

(x). Because f (0) 5 1.0472 . 0 and

f (π/2) 520.3180 , 0, the Intermediate Value Theorem tells us that f has a root c

in the interval (0, π/2). We calculate f

(x) 521 1 0.2056 cos (x). Because f

(x) ,2

1 1 0.2056 1 , 0, we can deduce that f is decreasing and the equation f (x) 5 0 has

only one solution. The graph of f in Figure 4 conﬁrms our analysis. From the graph,

it appears that x

5 1.2 is a good ﬁrst estimate. We let

ΦðxÞ5 x 2

f ðxÞ

ðxÞ

5 x 2

1:0472 2 x 1 0:2056  sin ðxÞ

2 1 1 0:2056  cosðxÞ

0.8 1.20.4

0.4

0.8

(

)

 1.0472  x  0.2056ⴢ sin

(

)

m Figure 4

(Sun)

m Figure 3

When a planet is at position P,

its

mean anomaly M is deﬁned by

M 5 2ðAreaðAFQÞ=

Þ.

4.8 The Newton-Raphson Method 351

and calculate

5 Φðx

Þ5 1:2419527

5 Φðx

Þ5 1:2417712

5 Φðx

Þ5 1:2417712:

Because |x

2 x

| , 5 3 10

, we can be reasonably sure that c 5 1.24177 is correct

to four decimal places.

Pitfalls of the Newton-

Raphson Method

Obviously the Newton-Raphson Method will go badly wrong if f

) 5 0 for some

index j. Look at Figure 5. We see that the tangent line at x

is horizontal, so of

course it never intersects the x-axis, and the method breaks down. In fact, there can

be trouble if f

) is small, even if it is not zero, because f (x

)/f

) can be large. If

this is the case, then x

j 1 1

will be far from x

even thou gh the root may be close to x

as is illustrated in Figure 6. In these circumstances, we say that the Newton-

Raphson Method diverges. The overshoot that causes this divergence can result in

convergence to a root other than the one that is sought (Figure 7). If an inﬂection

point is located close to a root, then the phenomenon of cycling may occur (see

Figure 8). The best thing to do when presented with one of these problems is to try

a different initial estimate.

A Computer

Implementation

The Newton-Raphson Method can be easily implem ented on a calculator or

computer. The next example shows how to put the method into action using

the computer algebra system Maple.

⁄ EX

AMPLE 4 The index of refraction r of a triangular glass prism satisﬁes

r sin



α 2



5 sinðθ

Þ;

where the angles α , θ

, and θ

are as in Figure 9. If α, θ

, and θ

are measured to be



,46



, and 54



respectively, then what is r to eight decimal places?

Solution Let

f ðrÞ5 r sin



46 π

180 r



2 sin



54π

180



As in most computations that involve the derivatives of trigonometric functions, we

con

vert to radian measurement of angles. Figure 10 then shows a solution using

Maple. Because |x

2 x

| , 5 3 10

, we can be reasonably cert ain that

r 5 2.08020645 is correct to 8 decimal places. (However, if α, θ

, and θ

have not

f(x

)  0

j–1

m Figure 5

j1

m Figure 8

m Figure 9 Refraction of light

by a triangular prism

j1

j1

m Figure 6

j1

j1

m Figure 7

352 Chapter

4 Applications of the Derivative

been measured to more than 2 signiﬁcant digits, then the extra digits in our answer

have no reliability.)

An Application in

Economics: Bond

Valuation

When a corporation or government issues a bond and sells it to an investor, the

issuer agrees to pay back (or redeem) the face value P to the investor in a speciﬁed

number n of years (at which time the bond is said to mature). If the coupon rate of

the bond is 100r% then, until the bond matures the issuer makes semi-a nnual

interest payments amounting to rP/2 each. For example, a bond with a $5000 face

value that pays $125 in interest every six months is said to have a 5% coupon rate

because r 5000/2 5 125 implies that r 5 0.05. After a bond has been issued, the

redemption value P and the coupon rate r do not change.

Because bondholders often want to sell bonds before their maturity, deter-

mining the market value of a bond is an important problem. The market price V of

a bond is rarely its face value P. As interest rates vary, the market price V of a bond

must adjust accordingly. For example, if interest rates have gone up because B was

issued, new bonds will have a higher coupon rate than B. The only way to sell bond

B is to offer it at a price V that is below its face value P.

An investor who redeems a bond will enjoy a capital gain (or suffer a capital

loss) if he has purchased the bond at a market price V that is less than (or greater

than) its redemption price P. This capital gain or loss must be considered in the

determination of the effective yield x of the bond. The effective yield x is expressed

by the formula

V 5 P 



ð1 1 xÞ



1 2 ð1 1 xÞ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

2 1



In practice, the investor will know the price V at which a bond is offered as well as

its coupon rate r, its face value P, and its maturity n. To make an informed decision,

the investor must determine the effective yield x. Because it is not feasible to solve

exactly for x, a root approximation method such as the Newton-Raphson Method is

necessary.

⁄ EX

AMPLE 5 A bond with a face value $10000, coupon rate 6

%; and

maturity of 20 years sells for $9125. What is the effective yield of the bond? (Bond

yields are customarily stated with two decimal places of accuracy.)

m Figure 1 0

4.8 The Newton-Raphson Method 353

Solution Here, P 5 10000, r 5 0.0675, n 5 20, and V 5 9125. Let

f ðxÞ5 10

000



ð1 1 xÞ

220

:0675



1 2 ð1 1 xÞ

220

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x 2 1



2 9125

and

Φ ðxÞ5 x 2

f ðxÞ

ðxÞ

Because there is a capital gain, the effective yield is greater than r. It therefore

makes sense to start our approximation process with a number x

greater than r.If

we choose x

5 0.07, then we calculate that

5 Φð0:07Þ5 0:07711

5 Φð0:07711Þ5 0:07753

5 Φð0:07753Þ5 0:07753:

(Clearly, f is quite complicated and Φ is even more so. The recorded values of Φ(x

)

have been obtained by using a computer algebra system.) The agreement between

and x

to two decimal places indicates that it is time to stop the algorithm. The

effective yield x is 7.75.%

QUICK QUIZ

1. If we wish to apply the Newton-Raphson Method to calculate 4

1/5

by setting

5 1 and letting x

n 1 1

5 Φ(x

) for n $ 1, then what function Φ can we use?

2. If we use the Newton-Raphson Method to ﬁnd a root of f (x) 5 x

1 2x 2 40 and

x 5 2 is our ﬁrst estimate of the root, then what is our second?

Answers

1. x 2 (x

2 4)/(5x

) 2. 84/41

EXERCISES

Problems for Practice

c In each of Exercises 126, use formulas (4.8.2) and (4.8.3)

together with the given initial estimate x

to ﬁnd the next two

estimates, x

and x

, of a root of the given function f. In each

case, x

will be accurate to at least two decimal places. b

1. f (x) 5 x

2 6, x

5 2

2. f (x) 5 x

1 2, x

521

3. f (x) 5 x

2 5x 1 2, x

5 4

4. f (x) 5 x

1 x 1 1, x

521

5. f (x) 5 x

2 24, x

5 2

6. f (x) 5 x

2 70, x

5 3

c In each of Exercises 7212,

a number is speciﬁed in the form

. Use formulas (4.8.2) and (4.8.3), the given initial estimate x

and a function f (x) 5 x

2 a

with p and q positive integers to

ﬁnd the next two estimates, x

and x

, of the given number. b

7. 4

1/3

, x

5 2

8. (25)

1/3

, x

522

9. 6

1/2

, x

5 2.5

10. (0.5)

3/2

, x

5 0.5

11.

ﬃﬃﬃﬃﬃ

, x

5 2

12. (27)

3/5

, x

523

Further Theory and Practice

13. If f is a nonconstant linear function, how many iterations

of the Newton-Raphson Method are required before the

root of f is found? Does your answer depend on the initial

estimate?

14. Suppose you are applying the Newton-Raphson Method

to a function f and that after ﬁve iterations you land

precisely on a zero of f. What value will the sixth and

subsequent iterations have?

15. Suppose that a given function f satisﬁes f (c) 5 0 and that,

in addition, there is an interval I about c such that

f ðxÞf

ðxÞ



, 1:

Then it is known that if the initial estimate is a point chosen

from the interval I then the Newton-Raphson Method will

354 Chapter 4 Applications of the Derivative