Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

certainly converge to c. Test each of the following functions

for this condition on the given interval:

a. f ðxÞ5 sin x; c 5 0; I 5 ð2π=4; π=4Þ

b. f ðxÞ5 x

2 x ; c 5 0; I 5 ð1=2; 2Þ

c. f ðxÞ5 x

1 8; c 522; I 5 ð23; 21Þ

d. f ðxÞ5 3x

2 12; c 5 2; I 5 ð1:5; 2:5Þ

16. It is interesting to observe that division can be accom-

plished numerically by an implementation of the Newton-

Raphson Method that does not involve any division at all.

Suppose that we wish to calculate α/β where β is nonzero.

The idea is to approximate 1/β andthenmultiplybyα.For

the approximation of 1/β, apply the Newton-Raphson

method to f (x) 5 β 2 1/x. What is the function Φ(x)of

formula (4.8.2)? (The formula involves multiplication and

subtraction, but not division.) If β 5 3andx

5 0.4, what

value does formula (4.8.3) yield for x

17. A Babylonian approximation to

ﬃﬃﬃ

from the second

millennium B.C. consists of starting with a ﬁrst estimate

and then computing the subsequent approximations

that are deﬁned iteratively by

j11





Show that this ancient algorithm is the Newton-Raphson

Method applied to f (x) 5 x

2 c. Of course there was no

notion of derivative when this algorithm was discovered.

Considering that x

j 1 1

is the average of x

and c/x

, what

might Babylonian mathematicians have had in mind when

they devised this algorithm?

18. Deﬁne

gðxÞ¼

ðx  4Þ

1=2

if x $ 4

ð4  xÞ

1=2

if x , 4

(

Prove that, for any initial guess other than x 5 4, the

Newton-Raphson Method will not converge.

19. If f is a function which is always concave up or always

concave down, if f

has no root, and if f has a root, then

the Newton-Raphson Method always converges to a root

no matter what the ﬁrst estimate. Explain why.

c In doing Exercises 20223,

refer to Exercises 84289 of

Section 4.2 for background on discrete dynamical systems.

Assume that f

exists and is continuous. b

20. Let Φ(x) 5 x 2 f (x)/f

(x). Suppose that f

) 6¼0. Show

that x

is an equilibrium point of the dynamical system

associated to Φ if and only if x

is a root of f.

21. Suppose that x

is a root of f and that |Φ

)| , 1 and that

is continuous on an open interval centered at x

. Show

that the sequence {x

} of Newton-Raphson iterates will

converge to x

provided that x

is sufﬁciently close to x

22. Show that |Φ

)| , 1 is equivalent to

f ðx

Þf

ðx

f ðx



, 1:

23. Deduce that under the hypotheses of the headnote, the

Newton-Raphson iterates will converge to the root x

of f

provided that x

is chosen sufﬁciently close to x

Calculator/Computer Exercises

24. Plot

f (x) 5 x

1 4x

1 6x

1 4x

1 1

in the viewing window [22.3, 0.5] 3 [23.25, 3]. You will

see that f has a root near 2 2.1. Apply the Newton-

Raphson Method using the initial estimate x

5 0. What

happens? Now try the initial estimate x

521.5 and cal-

culate x

through x

. Use the graph of f to explain

why 21.5, although not too distant from the root, is a poor

choice for x

. (In fact, when x

521.5 initializes the

Newton-Raphson process, x

is the ﬁrst approximation

that is closer to the root than the initial estimate.) Now

use the initial estimate x

526. What approximation does

give? (Notice that, because of the geometry of the

graph of f, the number 26, though not as close to the root

as 21.5, is a more efﬁcient choice for the initial estimate.)

c In each of Exercises 25228,

the given function has one real

root. Approximate it by making an initial estimate x

and

applying the Newton-Raphson Method until an integer n is found

such that |x

2 x

n 2 1

| , 5 3 10

. State x

, x

, ...,x

. b

25. f (x) 5 x

1 x

1 2x 2 5

26. f (x) 5 2x 1 cos ( x)

27. f (x) 5 5x

2 9x

1 15x

2 27x

1 10x 2 18

28. f (x) 5 x

1 3x

2 x

1 3x 2 2

c In Exercises 29 and 30 ﬁnd

the largest real root of the

given function f (x). b

29. f (x) 5 x 1 sin

(4.6x)/x

30. f (x) 5 x 1 tan ( x), x2 (2π,π).

31. Use the Newton-Raphson Method to approximate the

positive solution of

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

to 5 decimal

places.

32. The polynomial f (x) 5 x

1 x

2 1 has one root γ in the

interval [0, 1]. Find this root to ﬁve decimal places using

the Newton-Raphson Method.

c If (x 2 c)

is a factor of a polynomial p (x)but(x 2 c)

is not,

then c is a ro ot of p (x)ofmultiplicity 2. The graph of y 5 p (x)

touches the x-axis at a root of multiplicity 2 but does not cross

the x-axis there. In each of Exercises 33236,

plot the given

polynomial p (x) in the speciﬁed viewing rectangle. Identify a

rational number c that is a root of p with multiplicity 2. Use the

Newton-Raphson Method with initial estimate x

5 c 1 1/2 to

obtain iterates x

, x

, ...,x

. Terminate the process at the

smallest value of n for which |x

2 c| . 5 3 10

.WhatisN?

You will notice that the convergence is slow. Record the value

of N so that it can be used for comparison in Exercise 37. b

4.8 The Newton-Raphson Method 355

33. p (x) 5 x

2 2x

1 3x

2 4x 1 2, [22, 3] 3 [25, 50]

34. p (x) 5 x

1 x

2 6x

2 4x 1 8, [23, 0] 3 [22, 20]

35. p (x) 5 4x

2 4x

2 35x

1 36x 2 9, [23.2, 3.2]

3 [2125, 70]

36. p (x) 5 x

2 8x

1 23x

2 28x 1 12, [0.5, 3.5] 3 [20.25, 2.8]

37. A variant of Newton-Raphson for roots of higher multi-

plicity. Each polynomial in Exercises 3336 has one root

c of multiplicity m 5 2. Approximate each such root using

the initial estimate x

5 c 1 1/2 and the formula

j11

5 x

2 m

pðx

ðx

In each case, terminate the process at the smallest value of

M for which |x

2 c| , 5 3 10

.WhatisM? Compare the

number M with the corresponding number N that results

when the unmodiﬁed Newton-Raphson Method is used.

38. The atomic packing factor (APF) of a crystal is the

volume of a unit cube that is occupied by atoms. The APF

of NaCl is known to be 2/3. From the geometry of the

salt crystal, it can also be shown that the APF of NaCl is

given by

2πð1 1 r

3ð1 1 rÞ

;

where r is the ion size ratio of Na

and Cl

. Use the

Newton-Raphson Method to approximate r to 5 decimal

places.

39. The period T of a pendulum of length ‘ and maximum

deviation ϕ (measured in radians) from the vertical is

given approximately by

T 5 2π

ﬃﬃﬃ

‘



1 1

3072



If ‘ 5 0.8555 m. and T 5 2.000 seconds, what is ϕ. Use

g 5 9.807 m./sec

. and compute ϕ to four signiﬁcant digits.

40. A boat starts for the opposite shore of a 2 km wide river

so that (a) the boat always heads toward the point that is

directly across from the original launch point, and (b) the

speed of the boat is three times faster than the current of

the river. If we set up on an xy-coordinate system so that

the boat’s initial position is (2, 0), the landing site is at

(0, 0), and the current is in the positive y-direction, then

the path of the boat is given by

y 5





2=3





4=3

What are the x coordinates at the two points at which the

boat is 0.137 km downstream.

41. In each of the following parts, use the Newton-Raphson

Method to determine to 2 decimal places the effective

yield of the bond that is described.

a. A bond with a face value $10000, coupon rate 6

and maturity of 20 years that sells for $9125.

b. A bond with a face value of $10000, coupon rate 6.5%,

and maturity 10 years that sells for $10575.

c In each of Exercises 42245,

two $10000 bonds with the

same maturity are offered. Determine which is the better

investment by calculating the effective yield of each. b

42. Price 5 $10531,

coupon rate 5 7% or Price 5 $9146,

coupon rate 5 5%, n 5 10

43. Price 5 $8681, coupon rate 5 5% or Price 5 $10674,

coupon rate 5 7%, n 5 20

44. Price 5 $9518, coupon rate 5 6

% or Price 5 $8705,

coupon rate 5 6%, n 5 30

45. Price 5 $10679, coupon rate 5 8% or Price 5 $11052,

coupon rate 5 9%, n 5 8

46. The polynomial

1 3.6995x

2 4.04035x

2 16.13693x 1 6.83886

has two negative roots that are quite close to each other

and two positive roots. Use the Newton-Raphson method

to ﬁnd all four roots to ﬁve decimal places. Use a plot to

obtain suitable initial estimates.

47. Figure 8 illustrates the phenomenon of cycling with the

function f (x) 5 x 1 sin (x) and an initial estimate x

(0, 2) that leads, after two iterations, to x

5 x

. What

equation does x

satisfy? Use the Newton-Raphson

Method to approximate x

48. For every positive x,thenumberW (x)isdeﬁnedtobethe

unique positive number such that

W (x) exp (W (x)) 5 x.

The function x/W (x) is known as Lambert’s W func-

tion. Compute W (1) and W (e).

49. In biological kinetics, the equation

Y 5

x 1 3x

1 3x

1 10x

1 1 4x 1 x

1 4x

1 10x

represents a typical relationship between saturation Y

and dimensionless ligand concentration x (x $ 0). Use the

Newton-Raphson Method to ﬁnd the absolute maximum

value of Y /x.

356 Chapter 4 Applications of the Derivative

4.9 Antidifferentiation and Applications

It is useful in calculus to be able to reverse the differentia tion process. That is,

given a function f, we wish to ﬁnd a function F such that F

5 f. In this section, we

discuss this technique and ﬁnd some applications for it.

Antidifferentiation Let f be deﬁned on an open interval I.IfF is a differentiable function such that

(x) 5 f (x) for all x in I, then F is said to be an antiderivat ive for F on I.An

antiderivative is certainly not unique. That is because, if C is any constant, then

ðF 1 CÞðxÞ5



FðxÞ1 C



FðxÞ1

C 5 f ðxÞ1 0 5 f ðxÞ:

In other words, if F is an antiderivative for f on an interval I, then so is F 1 C for

any constant C. Every antideri vative G for f on I can, in fact, be accounted for in

this way: if F

(x) 5 f (x)andG

(x) 5 f (x) for all x in I, then F

(x) 5 G

(x)and

Theorem 5 from Section 4.2 tells us that G(x) 5 F(x) 1 C.

DEFINITION

The collection of all antideri vatives of a function f is denoted by

f ðxÞdx: ð4:9:1Þ

This expression is called the indeﬁnite integral of f. We refer to f (x) as the

integrand of expression (4.9.1). If F is a particular antiderivative of f, then, in

accordance with the preceding discussion, we write

f ðxÞdx 5 FðxÞ1 C; ð4:9:2Þ

where C represents an arbitrary constant. We refer to C as a constant of inte-

gration. The right side of (4.9.2) is interpreted to be the collection that consists

of each function of the form F (x) 1 C for some constant C.

⁄ EX

AMPLE 1 Calculate

dx:

Solution Becau

se differentiation of a power of x reduces the exponent by one, we

reverse our reasoning and guess that x

, which is one degree greater than x

, will be

an antiderivative. However,

5 4x

;

which is off by a factor of 4. We therefore adjust our guess to

FðxÞ5

Now we have

ðxÞ5

 4x

5 x

4.9 Antidifferentiation and Applications 357

as desired. Because all other antiderivatives for x

differ from this one by a constant,

we write our solution as

dx 5

1 C: ¥

INSIGHT

You may be surprised that the antidifferentiation process looks a bit

indirect. In fact, it is, but we will learn to antidifferentiate in an organized way. Chapter 6

is devoted to a wide variety of techniques for obtaining the antiderivatives of functions.

Antidifferentiating

Powers of x

Example 1 is an instance of a general principle that is worth isolating:

Indeﬁnite Integrals of Powers of x

The antiderivative of x

dx 5

m 1 1

m11

1 C for any m 6¼ 21:

ð4:9:3Þ

Indeed, for m 6¼2 1, we have



m 1 1

 x

m11



m 1 1

ðm 1 1Þx

5 x

Observe that we must exclude m 521 because the factor m 1 1 in the denominator is 0 for m 521. The next

example ﬁlls in this gap.

⁄ EX

AMPLE 2 Show that

dx 5 lnðjxjÞ1 C: ð4:9:4Þ

Solution Let f (x) 5 1/x for x 6¼0.

In Section 3.6 we learned that

ln ðxÞ5

for x . 0. This formula tells us that ln (x) is an antiderivative of f (x) on the interval

(0,N). Note, however, that 1/x is also deﬁned on (2N,0),butln(x)isnot.Wecan

repair this mismatch of domains by letting F (x) 5 ln (|x|). Because |x| 5 x on (0,N),

we see that nothing is changed on that interval: F (x) 5 ln (|x|) 5 ln (x)isan

antiderivative of 1/x for x . 0. On the other hand, for x , 0andu 5 |x|, we have

u 52x and

FðxÞ5

lnðuÞ5

lnðuÞ

ð2xÞ5

ð21Þ5

5 f ðxÞ:

In summary,

ln ðj x jÞ5

for every x 6¼0, which implies formula (4.9.4).

358 Chapter

4 Applications of the Derivative

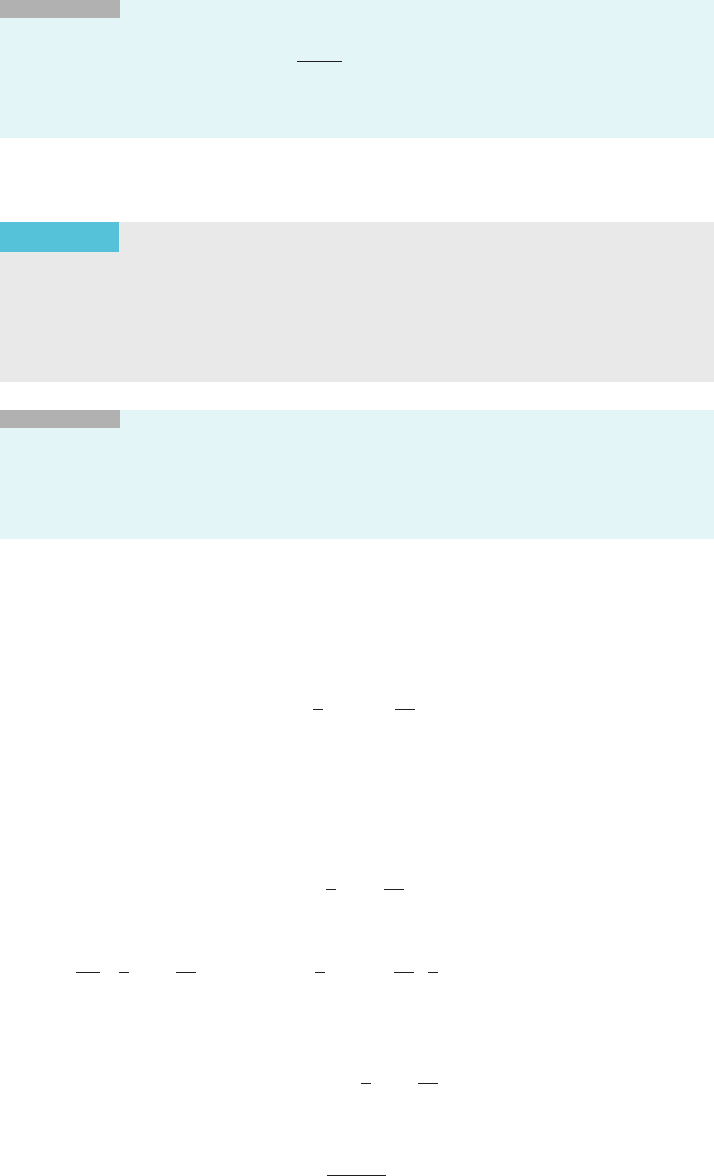
INSIGHT

Together, formulas (4.9.3) and (4.9.4) tell us

dx 5

m 1 1

m11

1 C if m 6¼ 21

lnðjxjÞ1 C if m 521:

We can restate some of the basic rules of differentiation in a form that is

helpful for antidifferentiaton:

THEOREM 1

Let f and g be functions whose domains contain an open interval

I. Let F be an antiderivative for f and G an antiderivative for g. Then



f ðxÞ1 gð x Þ



dx 5 FðxÞ1 GðxÞ1 C;

α  f ðxÞdx 5 α  FðxÞ1 C for any constant α:

INSIGHT

You may wonder why part a does not have two constants (because there

are two indeﬁnite integrals). The answer is that we can represent the sum of two arbitrary

constants by just another (single) arbitrary constant. Similarly, because a multiple of an

arbitrary constant is another arbitrary constant, there is no need to write the constant in

part b as α  C.

⁄ EXAMPLE 3 Calculate

ð3x

2 7x

3=2

2 4 Þdx:

Solution Ac

cording to Theorem 1a, we can solve this problem by antidifferentiating

in pieces. We can use formula (4.9.3) for each:

a. An antiderivative of x

is x

/6. Therefore an antiderivative of 3x

is 3x

/6, or x

/2.

b. An antiderivative for 7x

3/2

is 7 

5=2

,or

5=2

c. An antide rivative for 4 is 4x. (We can see that this antiderivative is correct by

differentiating it, but we can a lso derive it. If we write 4 as 4x

, then formula

(4.9.3) with m 5 0 tells us that

dx 5 x 1 C. Applying Theorem 1b with α 5 4

and f(x) 5 x

, we obtain

dx 5 4x 1 C.)

Putting calculations a, b, and c together yields the antiderivative

FðxÞ5

5=2

2 4x:

We check our work by differentiating:



5=2

2 4x



 6x



 x

3=2

2 4 5 3x

2 7x

3=2

2 4:

Because all other antiderivatives differ by a constant from the one we have

found, we write the solution as

ð3x

2 7x

3=2

2 4Þdx 5

5=2

2 4x 1 C: ¥

⁄ EXAMPLE 4 Calculate the indeﬁnite integral

ﬃﬃ

2 t

dt:

4.9 Antidifferentiation and Applications 359

Solution Algebraic manipulations can often simplify an integration problem.

After rewriting the indeﬁnite integral, we can use formula (4.9.2) and Theorem 1a

as follows:

ﬃﬃ

2 t

dt 5



1=2



dt 5

ðt

27=2

2 t

Þdt

25=2

ð25=2Þ

ð21Þ

1 C 52

25=2

1 t

1 C: ¥

Antidifferentiation of

other Functions

We may also antidifferentiate trigonometric functions and exponential functions.

For each differentiation formula from Chapter 3, there is a corresponding anti-

differentiation formula.

Derivative Formula Antiderivative Formula

sin xÞ5 cos xÞðð

cos ðxÞdx 5 sinðxÞ1 C

cos xÞ52sin xÞðð

sin ðx Þdx 52cos ðxÞ1 C

tan xÞ5 sec

xÞð



sec

ðxÞdx 5 tanðxÞ1 C

cot xÞ52csc

xÞð



csc

ðxÞdx 52cot xÞ1 C

sec xÞ5 sec xÞtan xÞððð

sec xÞtan xÞdx 5 secðxÞ1 Cðð

csc xÞ52csc xÞcot xÞððð

csc xÞcot xÞdx 52cos xÞ1 Cððð

5 e

dx 5 e

1 C

5 ln aðÞa

dx 5

ln aðÞ

1 C

arcsin



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 x

dx 5 arcsin



1 C

arctan



1 x

dx 5

arctan



1 C

arcsec



jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 a

jxj

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2 a

dx 5

arcsec



1 C

arctanh



2 x

dx 5

arctanh



1 C

arcsinh



ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

dx 5 arcsinh



1 C

⁄ EX

AMPLE 5 Calculate

sinð5xÞdx:

Solution We

recall that the derivative of cos (5x)is25 sin (5x). We need to adjust

our guess to eliminate the factor of 25. Therefore the antiderivative of sin (5x )

should be 2

cos ð5xÞ. We check that

360 Chapter 4 Applications of the Derivative



cosð5xÞ





25 sinð5x Þ



5 sinð5xÞ;

as desired. We write our solution as

sin ð5 x Þdx 52

cos ð5x Þ1 C: ¥

Velocity and

Acceleration

If a body moves in a linear path with position p(t) at time t, then the instantaneous

velocity of the body at time t is the instantaneous rate of change of position, or the

derivative of p:

vðtÞ5

ptÞ:ð

Similarly the acceleration of the body at time t is the instantaneous rate of change

of velocity, or the de rivative of v:

aðtÞ5

vðtÞ5



pðtÞ



pðtÞ:

In the language of antiderivatives, we have

Velocity is an antiderivative of acceleration.

Position is an antiderivative of velocity.

INSIGHT

If we measure distance p in feet and time t in seconds, then the average

rate of change of p with respect to t is expressed as

Δp feet

Δt seconds

This explains why the unit of measure for velocity is “feet per second” or ft/s.

Likewise, if velocity v is measured in ft/s, then acceleration is measured by considering

Δv ft=s

Δt s

This explains why the unit of measure for acceleration is “feet per second per second” or

ft/s

⁄ EXAMPLE 6 A police car accelerates from rest at a rate of 3 mi/min

. How

far will it have traveled at the moment that it reaches a velocity of 65 mi/hr?

Solution To

solve this problem, we let p(t) be the position of the police car at time

t (measured in minutes), v(t) its speed, and a(t) its acceleration. We begin with the

information

vðtÞ5 aðtÞ5 3:

Antidifferentiating, we ﬁnd that v(t) 5 3t 1 C, where C is the constant of integra-

tion. We recall that the car begins at rest, which means that the initial velocity is 0.

Thus 0 5 v (0) 5 3 0 1 C,orC 5 0. We have learned that v(t) 5 3t,or

4.9 Antidifferentiation and Applications 361

pðtÞ5 3t:

Antidifferentiating again, we ﬁnd that p(t) 5 3t

/2 1 D, where D is a constant of

integration. If we substitute t 5 0, we ﬁnd that p (0) 5 3 0

/2 1 D, or p (0) 5 D.

Thus

pðtÞ5

1 pð0Þ;

where p (0) is the initial position of the car. To answer the original question, we

convert the question to common units of minutes: How far has the police car

traveled when it is going 65/60 mi./min.? The time at which the car has reached

this velocity is obtained by solving v(t) 5 3t 5 65/60. We ﬁnd that t 5 65/180 min.

The car reaches the desired speed in 65/180 minutes (or 21.67 seconds). The

distance the car has traveled in this time is

pð65=180Þ2 pð 0 Þ5

ð65=180Þ

12675

64800

 0:1956 miles: ¥

⁄ EX

AMPLE 7 An object is dropped from a window on a calm day. It strikes

the

ground precisely 4 seconds later. From what height was the object dropped?

Solution To

answer this question, we need the fact (obtained from

experimentation) that the acceleration due to gravity of a falling body near the

earth’s surface is about 32.16 ft/s

.Ifh(t) is the height of the body at time t seconds

then we have

5 aðtÞ5232:16:

Notice the minu s sign, which indicates that the body is falling in the direction of

decreasing height. We antidifferentiate to ﬁnd that

5 vðtÞ5232:16t 1 C:

However, the initial velocity of the falling body is zero, so we ﬁnd that 0 5 v (0) 5

(232.16)  0 1 C; hence C 5 0 and

5232:16t:

Antidifferentiating again yields h(t) 5216.08t

1 D, where D is the constant of

integration. We do not know the initial height (this is what we seek), but we know

that after 4 seconds the height is zero. Therefore we may solve

0 5 hð4Þ5216:08  4

1 D

yielding D 5 257.28. Thus the height of the falling object at any time t is given by

h(t) 5216.08t

1 257.28. The answer to the original question is that the initial

height is h (0) 5 257.28 feet.

⁄ EXAMPLE 8 It is known that the acceleration due to gravity near the

surface of Mars is about 3.72 m/s

. If an object is propelled downward from a height

of 12 m with a speed of 72 km/hr, in how many seconds will it hit the surface of the

362 Chapter 4 Applications of the Derivative

Red Planet? What is the velocity at impact? (The data given describe the last 12

meters of the journey of Mars Pathﬁnder, which blasted into space on December 4

1996 and entered the Martian atmosphere on July 4 1997.)

Solution The

solution is pa rallel to that of Example 7, but the accel eration will be

different because the events are taking place on Mars.

Let h(t) deno

te the height of the body at time t. We begin with the equation

(t) 523.72 m/s

. We antidifferentiate to ﬁnd that h

(t) 5 v(t) 5 (23.72t 1 C) m/s.

We are told that the initial velocity of the falling body is 272 km/hr. We convert

this to meters per second:

vð0Þ5272

5272 

1000 m

3600 s

5220

On the other hand, v (0) 5 (23.72 0 1 C) m/s, or v (0) 5 C m/s. It follows that

C 5220. Substituting this value for C in the equation for h

gives us h

(t) 5

(23.72 t 2 20) m/s. Antidifferentiating this equation results in h(t) 5

(21.86 t

2 20t 1 D) m, where D is the constant of integration. We are given that

the initial height is 12 meters. Therefore 12 m 5 h (0) 5 (21.86 0

2 20 0 1 D)m,

or D 5 12 m. Thus the height of the falling object at time t is h(t) 5

(21.86 t

2 20t 1 12) m. From this equation we see that the body strikes the surface

of Mars when 0 5 h(t) 5 (21.86 t

2 20t 1 12). We solve this equation using the

quadratic formula, to ﬁnd that t 5211.3 or t 5 0.570 (to three signiﬁcant digits).

Only the second of these solutions is physically meaningful. We conclude that it

takes 0.570 seconds for the body to strike the surface of Mars. Finally, in the course

of our calculation we determined that v(t) 5 h

(t) 5 (23.72 t 2 20) m/s. The velo-

city at impact is therefore v (0.570) 5 (23.72 0.570 2 20) m/s 5222.1 m/sec.

QUICK QUIZ

1. Suppose that F(x) is an antiderivative of cos (x) such that F (π/4) 5

ﬃﬃﬃ

. What

is F (π/3)

2. True or false: There is exactly one antiderivative F (x)ofx

on (0,N) such

that F (1) 5 100.

3. True or false: There is no antiderivative F (x)of1/x on {x : x 6¼0} such that

F (21) 5 200 and F (1) 5 100.

4. True or false:

lnðjxjÞdx 5 1=x 1 C:

Answers

1. ð

ﬃﬃ

ﬃ

ﬃﬃﬃ

Þ=2 2. True 3. False 4. False

EXERCISES

Problems for Practice

c In each of Exercises 1220, calculate the indeﬁnite

integral. b

ðx

2 5xÞdx



3 sinðxÞ2 5 cosðxÞ1 1



sec ðxÞtan ðxÞdx

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

ðx

2 x

1 x

1=2

2 x

21=2

Þdx



1 x



3=2

ðx

2 4x

1 2x

Þdx

ðx 1 1Þ

10.

xðx 1 1Þðx 1 2Þdx

11.

exp ðe  xÞdx

12.

1=2

ðx 1 1Þdx

13.

ðx

27=3

2 4x

22=3

Þdx

14.

csc

ðxÞdx

4.9 Antidifferentiation and Applications 363

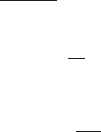
15.



3 cos





1 2x



16.



3 sinð7x



1 7 sinð3x



17.

sec





18.

csc





cotð2x



19.

ð3x 2 2Þ

20.

ﬃﬃﬃ

11Þ

c In each of Exercises 21225,

compute F(c) from the given

information. b

21. F

(x) 5 6x

, F (1) 5 3, c 5 0

22. F

(x) 5 2x 1 3, F (1) 5 2, c 521

23. F

(x) 5 cos (x), F (π/2) 521, c 5 π/6

24. F

(x) 5 1/x, F (1) 5 3, c 52e

25. F

(x) 5 6e

, F (0) 521, c 5 1/2

26. A car accelerates from rest at the constant rate of 2 mi/min

After the car has traveled one eighth of a mile, how fast will

it be traveling?

27. A sprinter accelerates during the ﬁrst 20 m of a race at the

rate of 4 m/s

. Of course, she begins at rest. How fast is

she running at the moment she hits the 20 m mark?

28. An object is dropped from a window 100 ft above

the ground. At what speed is the object traveling at the

moment of impact with the ground?

29. A baseball is thrown straight up with initial velocity

100 ft/s. How high will the ball go before it begins its fall

back to Earth? What will be the velocity of the ball, on

the way down, when it is at height 25 ft?

30. An automobile is cruising at a constant speed of 55 mi/hr.

To pass another vehicle, the car accelerates at a constant

rate. In the course of one minute the car covers 1.3 miles.

What is the rate at which the car is accelerating? What is

the speed of the car at the end of this minute?

31. A car traveling at a speed of 50 mi/hr must come to a halt

in 1200 ft. If the vehicle will decelerate at a constant rate,

what should that rate be?

32. A baseball is dropped from the top of a building. When it

strikes the ground its instantaneous velocity is 2 75 ft./sec.

How tall is the building?

33. A baseball is dropped from the top of a building which is

361 ft tall. How long will it take the ball to strike the

ground?

34. The acceleration due to gravity near the surface of the

moon is about 25.3064 ft/s

. If an object is dropped from

the top of a cliff on the moon, and takes 5 seconds to

strike the surface of the moon, then how high is the cliff?

Further Theory and Practice

c Use trigonometric identities to compute the indeﬁnite

integrals in Exercises 35241. b

35.

sin





cos





36.



cos





2 sin





37.

tan





38.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 cos





39.

cos





40.

cot





41.

sinðx



cos





42. Evaluate

dx :

43. Evaluate

xln





dx:

44. Evaluate

45. Suppose that f is continuous on R, that f is positive

on (2N, 23), (2, 4), and (4,N), and that f is negative on

(23, 2). If F is an antiderivative of f on R, classify the local

extrema of F.

46. If G is the antiderivative of g is G 3 f the antiderivative of

g 3 f? Why or why not?

47. Suppose that





dx 5 G





1 C. What is

gðf





Þf





dx?

c In each of Exercises 48252,

use the Chain Rule to calcu-

late the given indeﬁnite integral. b

48.



1 1



100

49.

2x cos



1 7



50.

sin





cos





51.

x exp





52.

cos ðsinð x



Þcos





53. Suppose that f and g are antiderivatives of f on an open

interval I and that F (x

) 5 G ( x

) for some point x

in I.

Show that F (x) 5 G (x) for every x in I. Show that this

conclusion is false if I is the union of two nonoverlapping

open intervals.

54. Find the constant A such that



1 1 e



dt 5 A



1 1 e



n11

1 C

for n 6¼21 and k 6¼0.

55. The error function, denoted erf (x), is deﬁned to be the

antiderivative of 2 exp (2x

ﬃﬃﬃ

whose value at 0 is 0.

What is the derivative of x/erf ð

ﬃﬃﬃ



56. Refer to the preceding exercise for the deﬁnition of the

error function erf. Where is erf increasing? On what

interval(s) is the graph of erf concave up? Concave down?

57. An arrow is shot at a 60



angle to the horizontal with

initial velocity 190 ft/s. How high will the arrow travel?

What will be the horizontal component of its velocity at

height 50 feet (going up)?

58. In a light rail system, the Transit Authority schedules a 10

mile trip between two stops to be made in 20 minutes. The

train accelerates and decelerates at the rate of 1/3 mi/min

364 Chapter 4 Applications of the Derivative