Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Iftheengineerspendsthesameamountoftimeaccelerating

and decelerating, what is the top speed during the trip?

59. The engineer of a freight train needs to stop in 1700 feet in

order not to strike a barrier. The train is traveling at a

speed of 30 mi/hr. The engineer applies one set of brakes,

which causes him to decelerate at the rate of 1/5 mi/min

Fifteen seconds later, realizing that he is not going to make

it, he applies a second set of brakes, which, together with

the ﬁrst set, causes the train to decelerate at a rate of 3/10

mi/min

. Will the train strike the barrier? If not, with how

many feet to spare? If so, at what speed is the impact?

60. A speeding car passes a policeman who is equipped with a

radar gun. The policeman determines that the car is doing

85 mi/hr. By the time the policeman is ready to give chase,

the car has a 15 second lead. The policeman has been

trained to catch vehicles within 2 minutes of

the beginning of pursuit. At what constant rate does the

police car need to be able to accelerate to catch

the speeding car?

61. A woman decides to determine the depth of an empty

well by dropping a stone into the well and measuring how

long it takes the stone to hit bottom. She drops the stone

into the well and hears it hit bottom 6 seconds later.

However sound travels at the approximate speed of

660 mi/hr. So there is a delay from the time that the stone

hits bottom to the time that she hears it. Taking this delay

into account, determine the depth of the well.

62. Visitors to the top of the Empire State Building in New

York City are cautioned not to throw objects off the roof.

How much damage could a one ounce weight dropped

from the roof do? The height of the building is 1250 feet.

Using the quantity mass 3 velocity, which is momentum,

as a measure of the impact of the weight when it strikes,

compare your answer with the impact of a ten ounce

hammer being swung at a speed of ten feet per second.

63. A model rocket is launched straight up with an initial

velocity of 100 ft/s. The fuel on board the rocket lasts for 8

seconds and maintains the rocket at this upward velocity

(countering the negative acceleration due to gravity).

After the fuel is spent then gravity takes over. What is the

greatest height that the rocket reaches? With what velo-

city does the rocket strike the ground?

64. The initial temperature T (0) of an object is 50



C. If the

object is cooling at the rate

ðtÞ520:2e

20:02t

when measured in degrees centigrade per second, then

what is the limit of its temperature as t tends to inﬁnity?

65. At a given moment in time, two race cars are abreast and

traveling at the speed of 90 mi/hr. Car A then begins to

accelerate at a constant rate of 6 mi/min

and Car B

begins to accelerate at a constant rate of 9 mi/min

. The

cars are driving on a track of circumference 2 miles. How

long will it take Car B to lap Car A three times?

66. If a car that is initially moving at 100 km/hr decelerates to

0 at a constant rate r in 60 m, what is r?

67. If the air resistance to a falling object is proportional to

the velocity of that object, then the velocity of that object

when dropped from a height H is

vðtÞ52kgð1 2 e

2t=k

Þ:

Here k is a positive constant and g is the constant accel-

eration due to gravity. Calculate the height y of the object

as a function of t.

68. If the air resistance to a falling object is proportional to

the square of the velocity of that object, then the accel-

eration of that object is given by

aðtÞ524ge

ﬃﬃﬃﬃ

gκ

ðe

ﬃﬃﬃﬃ

gκ

1 1Þ

where g is the acceleration due to gravity and κ is a

positive constant. Find the velocity v of the object as

a function of t assuming that v(0) 5 0. Hint: First do

Exercise 54.

Calculator/Computer Exercises

69. Suppose that the rate of change of the mass m of a sample

of the isotope

C satisﬁes

ðtÞ520:1213  e

20:0001213t

when t is measured in years. If m (0) 5 1000 g, then for

what value of t is m (t) equal to 800 g?

70. The amount y of an isotope satisﬁes

52k yð0Þe

2kt

when t is measured in years and y (0) is measured in

grams. If, after one year, the amount y is one-third the

initial amount y (0), then what is the value of k?

71. The initial temperature T(0) of an object is 50



C. If the

object is cooling at the rate

ðtÞ520:2e

20:02t

when measured in degrees centigrade per second, what is

the limit T

of its temperature as t tends to inﬁnity? How

much time τ

does it take for the object to cool 4



C (from



Cto46



C)? How much additional time τ

elapses

before the object cools an additional 2



C? How much

additional time τ

elapses before the object cools an

additional 1



C (from 44



Cto43



C)?

72. Suppose the velocity of an object when dropped from a

height 100 m is

vðtÞ5219:6ð1 2 e

2t=2

Þm=s:

4.9 Antidifferentiation and Applications 365

(This equation can arise when air resistance is propor-

tional to velocity.) Calculate the height y of the object as

a function of t. Use the Newton-Raphson Method to

compute the time t of descent. Plot y (t) for 0 # t # T.

73. Suppose the acceleration of an object when dropped from

a height 100 m is

aðtÞ5239:2  e

4:427t

ð11e

4:427t

(This equation can arise when air resistance is propor-

tional to the square of the velocity.) Calculate the

downward velocity v if v (0) 5 0. (Look at Exercise 54 to

do this part.) Plot v (t) as a function of t. What is the

“terminal velocity”

5 lim

t-N

vðtÞ?

Use the Newton-Raphson Method to determine the value

of t for which v (t) 5 0.999 v

74. After jumping from an airplane, a skydiver has downward

velocity given by

vðtÞ52192ð1 2 e

2t=6

Þft=s:

Twelve seconds into his descent, the skydiver opens his

parachute. For t . 12 his velocity is given by

vðtÞ5



16 2 192ð1 2 e



2422t

2 16 ft=s:

a. Graph the skydiver’s velocity. Is it everywhere con-

tinuous? Differentiable?

b. Graph the skydiver’s acceleration. Is it everywhere

continuous? Differentiable?

c. Determine the skydiver’s “terminal velocity”

5 lim

t-N

vðtÞ:

d. If the skydiver jumped from 3000 feet, calculate his

height function.

e. How long does the ﬁrst half of his jump, that is the ﬁrst

1500 feet, take? How long does the second half take?

75. The sine integral Si is deﬁned to be the antiderivative of

sin (x)/x such that Si (0) 5 0. Analyze the graph of Si (x)

over 2 4π # x # 4π for intervals of increase and decrease

and for upward and downward concavity. Explain your

analysis. Then use a computer algebra system to graph

Si (x) over this interval.

Summary of Key Topics in Chapter 4

Related Rates

(Section 4.1)

If two variables x and y are

related by an equation F (x, y) 5 C,ifx depen ds on a

third variable t, and if dx/dt is known, then the Chain Rule together with the

method of implicit differentiation (when needed) can be used to ﬁnd dy/dt.

Local and Absolute

Maxima and Minima

(Section 4.2)

Let f be

a function with domain S. We say that f has a local maximum at a point c 2

S if there is a δ . 0 such that f (c) $ f (x) for all x 2S such that jx 2 cj , δ. We say

that f has a local minimum at c if there is a δ . 0 such that f (c) # f (x) for all x 2S

such that jx 2 cj , δ.

We call c an absolute minimum or maximum in case the above inequalities

hold for all x in S. The locations of local/global maxima and minima are called

local/global extrema. If f is differentiable on an open interval I and if c 2 I is an

extremum then f

Rolle’s Theorem and

the Mean

Value Theorem

(Section 4.2)

Let f be

continuous on [a, b] and differentiable on (a, b) and suppose that f (a) 5

f (b). Then there is a number c 2(a, b) such that f

More generally, let f be continuous on [a, b] and differentiable on (a, b). Then

there is a c 2(a, b) such that

ðcÞ5

f ðbÞ2 f ðaÞ

b 2 a

366 Chapter 4 Applications of the Derivative

A consequence of the mean value theorem is that if f is differentiable on an open

interval I and f

5 0onI then f is a constant function. As a consequence, if two

functions f and g have the same derivative function then they differ by a constant.

Critical Points

(Section 4.3)

A point where either f

5 0orf

is undeﬁned is called a critical point.

Increasing and

Decreasing Functions

(Section 4.3)

If f

. 0 on an open interval I then f is increasing on I.

If f

, 0 on an open interval I then f is decreasing on I.

The First Derivative

Test for Extrema

(Section 4.3)

Let c be

a critical point for a differentiable function f.

a. If there is a δ . 0

such that f

, 0on(c 2 δ, c)andf

. 0on(c, c 1 δ), then c is a

local minimum.

b. If there is a δ . 0

such that f

. 0on(c 2 δ, c)andf

, 0on(c, c 1 δ), then c is a

local maximum.

Applied Maximum-

Minimum Problems

(Section 4.4)

The ability to locate extrema of functions enables us to solve a variety of applied

problems.

In these applied problems, we often must ﬁnd the extrema of a con-

tinuous function on a closed and bounded interval. We seek the extrema at the

endpoints and the critical points.

Concavity, Points of

Inﬂection, Second

Derivative Test

(Section 4.5)

If f

increases on an open interval I then the graph of f is said to be concave up on I.

If f

decreases on an open interval I then the graph of f is said to be concave down

on I.

In case f

. 0onI then f is concave up on I;iff

, 0onI then f is concave

down on I. A point of inﬂection for a function is a point where the concavity

changes from down to up or up to down.

If f is differentiable on an open interval containing c and if c is a critical point

then we have:

a. If f

b. If f

c. If f

Graphing

(Sections 4.2, 4.3, 4.5, 4.6)

We note that differentiable functions are continuous, making graphing simpler.

The

concepts of increasing, decreasing, critical point, point of inﬂection, concave

up, and concave down enable us to draw very sophisticated sketches of curves.

I’Ho

pital’s Rule

(Section 4.7)

If c is

either a real number or 6N and if lim

x-c

f ðxÞ5 lim

x-c

gðxÞ5 0

or lim

x-c

f ðxÞ5 lim

x-c

gðxÞ5 N then

Summary of Key Topics 367

lim

x-c

f ðxÞ

gðxÞ

5 lim

x-c

ðxÞ

g ðxÞ

With algebraic manipulation, l’Ho

pital’s Rule can also be used to treat the inde-

terminate forms 0 N and N2N. After an application of the logarithm, l’Ho

pital’s

Rule can be used to treat the indeterminate forms 0

,andN

The Newton-Raphson

Method

(Section 4.8)

If x

is a good initial estimate to a root c of a differentiable function f, then the

sequence of iterates {x

} obtained by

n11

5 x

f ðx

ðx

is often used to approximate c.

Antidifferentiation

(Section 4.9)

Given a function f,

it is useful to be able to determine functions F such that F

5 f.

We call f an antiderivative for f and write

f ðxÞdx 5 FðxÞ1 C. The expression

f (x) dx is called an indeﬁnite integral. Indeﬁnite integrals can be used to study

problems about velocity and acceleration of moving bodies.

Review Exercises for Chapter 4

c In each of Exercises 124, variables x and y are related by a

given equation. A point P

on the graph of that equation is also

given. Use the given value of v



to calculate



. b

x 1 y

5 1 1 x

; P

5 ð3; 5Þ; v

5 2

xy 5 y

1 2; P

5 ð5; 2Þ; v

523

3. y=x 1 2=y 5 6; P

5 ð1=4; 1=2Þ; v

523

4. y 1 exp xy 5 3; P

5 ð0; 2Þ; v

5 2

5. A snowball is melting so that its surface area decreases at

the rate of 3 cm

/min. At what rate is the radius r

decreasing when r 5 4?

6. As the sun sets, rays passing just over the top of a 20 m

building make an angle θ with Earth that changes at the

rate of 22π/(24 60) radians per minute. How fast is the

shadow of the building lengthening when θ 5 π/6?

7. A heap of sand in the shape of a right circular cone of

height h and base radius r has volume πr

h/3. The volume

of the heap is constantly 8π\m

, but, as surface grains

slide down the side, the radius r increases at the rate of 3/

160 m/min. At what rate is the height decreasing when

r 5 3/2 m?

8. The lateral surface area of a right circular cone of height h

and base radius r is πr

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 h

. The cone increases in size

in such a way that h 5 4r/3 and dA/dt 5 20π cm

/s. How

fast is the radius increasing when the height is 24 cm?

9. A particle moves along the curve y 5 1/x.Whent 5 7, the

x-coordinate of the particle’s position is 1/6 and dx/dt 5 3.

At t 5 7 how fast is the sum of the particle’s coordinates

changing?

10. A 13 foot ladder leans against a wall. The foot of the

ladder is being pushed toward the wall at the rate of

1/2 ft/s. When the foot of the ladder is 5 ft from the

wall, how fast is the top of the ladder rising?

11. A rope extends in a straight line from the deck of a boat to

a pulley at the edge of the dock. The level of the pulley is 6

ft above the boat’s deck. The rope is being reeled in at the

rate of 2/5 ft per second. How fast is the boat approaching

the dock when it is 8 ft away?

12. A photographer stands at point Q that is 6 ft away from

point P on a straight track (with

PQ being perpendicular

to the track). The photographer focuses a camera on a

runner whose rate is 18 ft/s. When the runner is 8 ft from P,

how fast is the camera rotating?

c In each of Exercises 13216,

calculate the values c in I and

the given function f on the given interval I. b

13.

f ðxÞ5 x

; I 5 ½1; 4

14.

f ðxÞ5 1=

ﬃﬃﬃ

; I 5 ½1=16; 1=4

15. f ðxÞ5 1=x; I 5 ½2 27; 23

16.

f ðxÞ5 ln ðjxjÞ; I 5 ½2e

; 21

368 Chapter 4 Applications of the Derivative

c In each of Exercises 17220, calculate the value c in I that

arises when Rolle’s Theorem is applied to the given function f

on the given interval I. b

17. f ðxÞ5 x 1 1=x; I 5 ½23; 21=3

18.

f ðxÞ5 xð1 2 x

Þ; I 5 ½0; 1

19.

f ðxÞ5

x 2 e

1 2 e

1 lnðxÞ; I 5 ½1; e

20.

f ðxÞ5 x 2

ﬃﬃﬃ

; I 5 ½1=16; 9=16

c In each of Exercises 21224,

use the given information to

ﬁnd F (c). b

21.

ðxÞ521=x

1 1=x; Fð1Þ5 7; c 5 1=2

22. F

ðxÞ5 4 sinðxÞ; Fð π=3Þ5 3; c 5 π

23.

ðxÞ5 4=x; Fðe

Þ5 7; c 5 e

24.

ðxÞ5 secðxÞ

; Fðπ=4Þ5 0; c 5 π=3

c In each of Exercises 25238,

ﬁnd all critical points of the

function f deﬁned by the given expression. Then use the First

Derivative Test to determine whether each critical point is a

local maximum for f, a local minimum, or neither. b

25. x

2 12x 1 1

26. 4x

2 x

27. x

2 48 ln ðxÞ

28. 3x

2 4x

2 30x

2 36x 1 7

29. x

1 48=x

30. ln ðxÞ=x

31. ln

ðxÞ=x

32. x 2 12x

1=3

33.

ﬃﬃﬃ

=ðx 1 5Þ

34. ðx

2 3x

2 4x 2 8Þ=ðx 1 1Þ

35. x

=2 2 4x 1 6lnðx 1 1Þ

36. ð6x

1=3

37. x

2 3x

1 3x

2 x

1 2

38. ðx

1 6x 2 6Þ=e

c In each of Exercises 39242, calculate the minimum and

maximum values of the given function f on the given interval I. b

39.

f ðxÞ5 x

2 12x 1 2; I 5 ½23; 5

40.

f ðxÞ5 2x

2 3x

; I 5 ½21; 2

41. f ðxÞ5 xe

; I 5 ½21; 2

42.

f ðxÞ5 xðx21Þ

2=3

; I 5 ½1=2; 3=2

43. A Norman window has the shape of a rectangle sur-

mounted by a semicircle. If the perimeter is 5 m, what

base length maximizes the area?

44. When a person coughs, air pressure in the lungs increases

and the radius r of the trachea decreases from the normal

value ρ. Units can be chosen so that the speed v of air in

the trachea is given by v 5 (ρ 2 r)r

. For what value of r/ρ

is v maximized?

45. The surface area A of a cell in a beehive depends on two

side lengths, a and b, and an acute angle θ that determines

the shape of the opening to the cell. The formula is

AðθÞ5 6ab 1



ﬃﬃﬃ

csc ðθÞ2 cotðθÞ



Show that for any positive constants a and b, the surface

area is minimized when sec (θ) 5

ﬃﬃﬃ

46. A 12 inch piece of wire can be bent into a circle or a

square. Or, it can be cut into two pieces. In this case a

circle will be formed from the ﬁrst piece and a square

from the other. What is the minimal area that can result?

(Example 4 from Section 4.4 is similar but examines the

maximal area instead.)

47. Consider the two curves y 5

ﬃﬃﬃ

and y 5 x

for 0 # x # 1:

What is the longest horizontal line segment between the

two curves?

48. A rectangular box is twice as wide as it is deep. If the

volume of the box is 144 in

, then what is the smallest

total surface area of its six faces?

49. A rectangular box is twice as wide as it is deep. If the total

surface area of its six faces is 144 in

, then what is the

smallest volume?

c In Exercises 50259,

ﬁnd (a) the interval(s) on which the

graph of the given function f is concave up, (b) the interval(s)

on which the graph of f is concave down, (c) and the inﬂection

points of f, if any. b

50. f (x) 5 x

1 9x

2 x 1 1

51. f (x) 5 x

2 6x

1 7x 1 3

52. f (x) 5 x/(x

1 27)

53. f (x) 5 e

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 e

54. f (x) 5 x

55. f (x) 5 3/x 1 ln (x)

56. f (x) 5 x

1 48 ln (x)

57. f (x) 5 ln (x)/x

58. f (x) 5 x

1/3

1 x

59. f (x) 5 x

4/5

(x 2 27)

c In Exercises 60273,

evaluate the given limit. (For some of

these limits, l’Ho

pital’s Rule is not the most effective

method.) b

60. lim

x-N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

61. lim

x-N

1 x

1 2x

62. lim

x-0

sinð5xÞ

sinð3xÞ

63. lim

x-π=8

cosð12xÞ

cosð4xÞ

64. lim

x-0

tanð20xÞ

tanð4xÞ

65. lim

x-π=2

ð2x 2 πÞ

cotðxÞ

66. lim

x-0

x sinðxÞ

sinðx

Review Exercises 369

67. lim

x-N

2x=2

68. lim

x-0

1 e

22x

2 2 2 x

69. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 8x

2 xÞ

70. lim

x-1N

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 6x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 9

71. lim

x-N



x 2 2

x 1 1



72. lim

x-0

2=ln ðxÞ

73. lim

x-0



2 1



c In Exercises 74277,

ﬁnd the next two approximations to

the root of f (x) 5 0 using the Newton-Raphson Method. b

74. f (x) 5 x 2 exp

(2x), x

5 1.0

75. f (x) 5 2 1 ln (x) 2 x, x

5 4.0

76. f (x) 5 xe

2 3, x

5 1.0

77. f (x) 5

ﬃﬃﬃ

1 1=

ﬃﬃﬃ

2 3; x

5 8.0

c In each of Exercises 78290,

calculate the indeﬁnite

integral. b

78.

79.

sec ðxÞtanðxÞdx

80.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

x 1 2

81.

ð3x11Þ

82.

1 3x

83.

xðx 2 1Þðx 1 1Þdx

84.

x13

85.

ðx

4=3

2 4x

21=3

Þdx

86.



3 sinðxÞ1 cosð3xÞ



87.

sec

ð3xÞdx

88.

csc ðxÞcotðxÞdx

89.

ﬃﬃﬃ

1 2Þdx

90.

ð2x

Þdx

370 Chapter 4 Applications of the Derivative

GENESIS

DEVELOPMENT4

Fermat’s Life

In the center of Toulouse, France, lies a beautiful civic

building called the Capitole; in this building is a large

statue of Pierre de Fermat, seated with a sign declaring

him to be the father of differential calculus. A muse is

nearby, showing her abundant appreciation for his

mental powers. Whereas mathematicians today either

work for universities, government, or industry, in

Fermat’s day many mathematicians were amateurs.

Fermat was a judge by profession, and rather a wealthy

man. He was a cultured man and a supporter of the

arts. He wrote his native French elegantly and was

ﬂuent in Italian, Spanish, Latin, and classical Greek.

Although he developed a reputation as a classicist and

a poet, his special passion was for mathematics.

Fermat was born in the small town of Beaumont-de-

Lomagne in the year 1601. Sometime in the 1620s,

Fermat studied at the University of Bordeaux with fol-

lowers of Franc¸ois Vie

te, the leading French mathema-

tician of an earlier generation. Fermat went on to study

law at the university at Orl

eans, attaining his degree in

1631. He served as magistrate in a special court in

Castres that had been created to settle disputes among

Protestants and Catholics. It was in Castres, in 1665, that

Fermat died. Ten years later, his remains were trans-

ferred to the Church of the Augustines in Toulouse.

Fermat’s Investigation of Extrema

In 1629 Fermat joined a project that aimed to use

the surviving commentaries of Pappus to reconstruct

the lost books of Apolloniu s. While working on this

project, sometim e before 1636, Fermat hit upon the

idea of analytic geometry. He wrote up his discovery in

1636 and circulated it in Paris in 1637, prior to the

publication of La G

eometrie of Descartes. In 1637

Fermat also published his method of maxima and

minima, which we now call Fermat’s Theorem.

After demonstrating his method on a simple

classical problem, Fermat proposed and answered the

following problem: divide a line segment of length b

into two pieces such that the product of the length of

one by the square of the length of the other is a max-

imum. In other words, maximize

f ðxÞ5 ðb 2 xÞx

5 bx

2 x

; 0 # x # b:

Supposing that this maximum occurs at x 5 a, Fer-

mat set f (a) 5 f (a 1 h) and worked with the equation

f ða 1 hÞ2 f ðaÞ

5 0

bða1hÞ

2 ða1hÞ

2 ðba

2 a

5 0:

This simpliﬁes to (2ab 2 3a

) 1 (b 2 3a)h 2 h

5 0.

Either by discarding the remaining terms that involve h

or by setting h 5 0, Fermat concluded that

2ab 2 3a

5 0 and a 5 2b/3. Fermat did not use lan-

guage that suggests that he considered h to be inﬁni-

tesimal or even small: his approach was an algebraic

one that he developed before his discovery of analytic

geometry. The derivative had not yet been invented

and it was this very investigation that led Fermat to

introduce it, staking his claim to be “father of the dif-

ferential calculus.’

Fermat’s Investigation of Points of Inﬂection

The notion of point of inﬂection arose very early in the

study of the tangent problem. In letters written to

Fermat in 1636, Roberval suggested that the curve

known as the conchoid has two points at which there

are no tangent lines. What Roberval had discovered

and was referring to is that the conchoid has two points

of inﬂection. The graph of the conchoid (together with

one of its tangent lines at an inﬂection point) appears

in Figure 1. Roberval called attention to the change in

concavity at B by describing the conchoid as “convex

on the outside” from A to B and “convex on the inside”

from B through c to inﬁnity.

Fermat addressed this issue in a let ter to Mersenne

dated 20 April 1638. Fermat’s discussion indicates that

he continued to think of his Tangent Method as a

y  f(x)

m Figure 1 A conchoid and a tangent at a point of inﬂection

371

by-product of his Method of Maxima/Minima. He

wrote to Mersenne: “ . . . in order to properly graph

the [conchoid], it is appropriate that we investigate the

points of inﬂection, where the curvature becomes con-

cave or convex, or vice versa. This question is elegantly

resolved by the Method of Maxima/Minima by virtue of

the following general lemma.” Fermat continued by

asserting that among all tangents to the conchoid, the

tangent at the inﬂection point is distinguished by mini-

mizing the angle θ made with the positive x-axis. This is

the same thing as minimizing tan(θ) 5 f

(x). Because

Fermat’s Theorem gives (f

)

(x) 5 0 as a necessary

condition for this minimum, Fermat had, in effect, dis-

covered a necessary condition for (x, f (x)) to be a point

of inﬂection, namely f

(x) 5 0.

Fermat’s Principle of Least Time

Although Fermat had little interest in physics, he did

turn his consideration to one particular question in

optics. Therein lies another bitter dispute with Des-

cartes. This particular quarrel be gan with an early

correspondent of Fermat, Jean de Beaugrand. Beau-

grand’s major work, G

eostatique (1636), had received

severe criticism from Descartes, who wrote

“Although I have seen many squarings of the circle,

perpetual motions, [etc.] . . . I can say nonetheless

that I have never seen so many errors combined in

one postulate. I can therefore conclude that the

contents of G

eostatique are so irrelevant, ridiculous,

and mistaken, that I wonder if any honest man has

ever troubled himself to read it.”

Beaugrand retaliated by circulating three pamph-

lets in which he charged Descartes with plagiarism.

Also, using his position as Secr

etaire du Roi, Beaugrand

obtained a printer’ s copy of Descartes’s La Dioptrique

prior to its publication. Beaugrand distributed copies in

the hope that embarrassing prepublication criticism

would ensue. Fermat was one of the recipients.

In an April or May 1637 commentary on La

Dioptrique, Fermat drew attention to errors that Des-

cartes had made in his derivations of the Laws of

Reﬂection and Refraction. Descartes was not pleased.

The situation between the two grew more tense when,

after reading La G

eometrie, Fermat sent Descartes

documents that established his priority in the matters of

analytic geometry and the tangent problem.

Eight years after the death of Descartes, in 1658,

the edito r of the Letters of Descartes, Claude Clerselier,

found two letters from Fermat among the papers of

Descartes. He asked Fermat for copies of any other

letters that he might have sent to Descartes. Because

Fermat had only written the two that had been found,

he interpreted the request to be a reopening of the

optics controversy.

Fermat argued that there were three fundamental

ﬂaws that invalidated Descartes’s treatment of refraction:

Descartes did not understand what a valid demonstration

should be, Descartes had not argued consistently even

within his own incorrect logical framework, and Descartes

had based his derivation on the patently false notion that

the denser is the medium, the easier is the passage of light

through it. Experts warned Fermat to be more cautious:

experimentation conﬁrmed the Law of Refraction that

Descartes had published.

At about this time, Fermat received the Trait

edela

Lumi

e of Marin Cureau de la Chambre (1594, Mans -

1669, Paris). In it was a derivation of the Law of

Reﬂection based on the method of minimiz ation.

Suppose that a ray of light emitted from A is reﬂected

by the straight line ECF and arrives at B, as in Figure 2.

The law of reﬂection states that the angle of incidence

ACG equals the angle of reﬂection GCB. Cureau

derived this from the postulate, that light travels from

A to EF to B in the least distance. That is, for any other

point D on EF, AC 1 CB , AD 1 DB. This inequality

follows easily from classical geometry.

Fermat saw that, if he reformulated Cureau’s

principle as a least

time postulate, then he would be

able to apply calculus to the more complicated phe-

nomenon of refraction. With refraction we suppose

that the points A and B are in different media, sepa-

rated by boundary EF as in Figure 3. Light travels with

speed v

in the medium containing point A and with

speed v

in the medium containing B. The Law of

Refraction asserts that

sin ðαÞ

sin ðβÞ

DEC

m Figure 2

372 Chapter

4 Applications of the Derivative

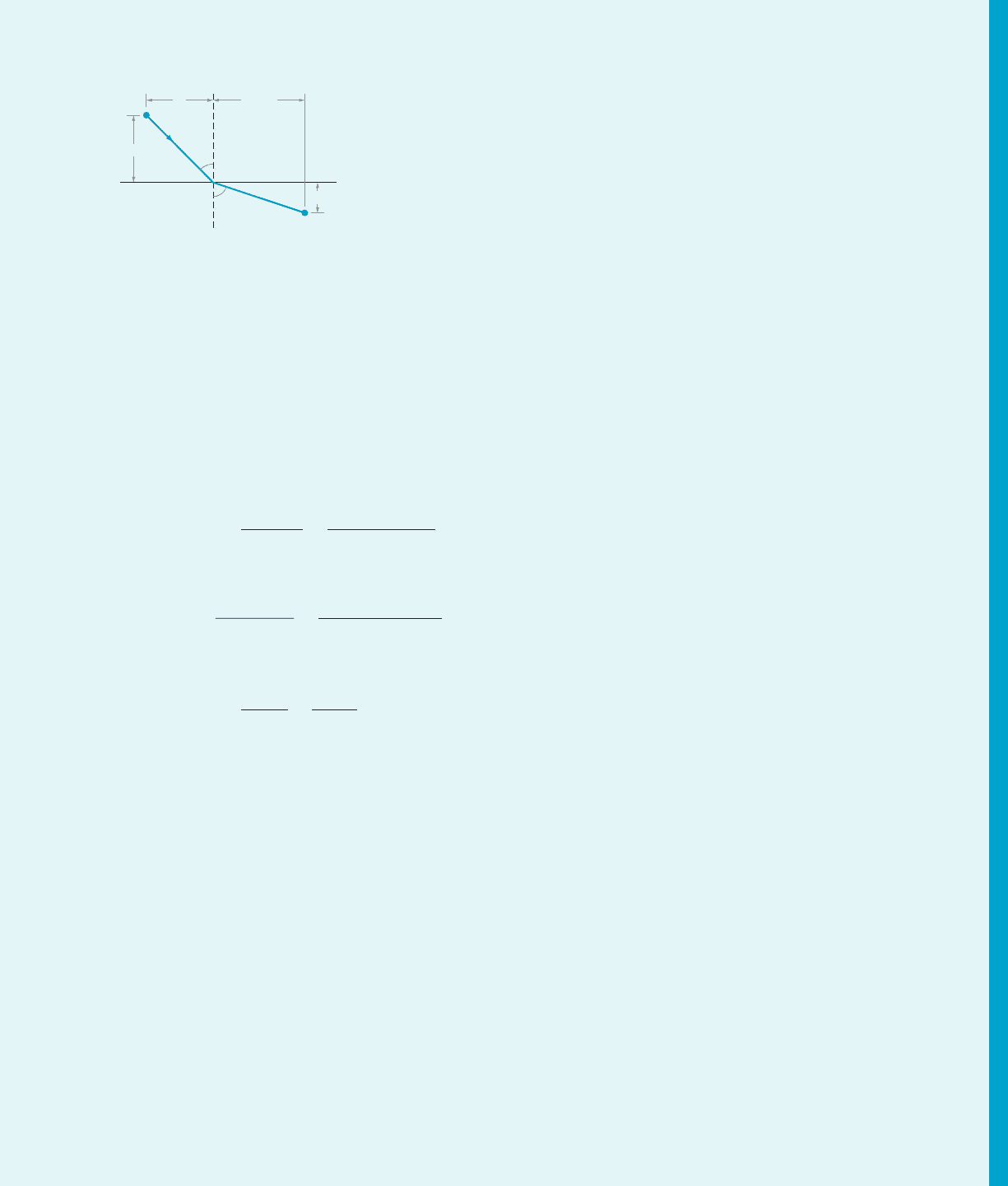
where α is the angle of incidence and β is the angle of

refraction (as in Figure 3). Fermat supposed that the

point C at which the ray of light impinged on EF was

such that the light ray travelled from A to C to B in

least time. This general princ iple is now known as

Fermat’s Principle of Least Time. From this principle,

Fermat derived the Law of Refraction. We see from

Figure 3 that the total time required for the light ray to

reach B from A by impinging on EF at a point whose

abscissa is x beyond A is

f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 ðd 2 xÞ

We therefore set

ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 x

d 2 x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 ðd 2 xÞ

5 0

sin ðαÞ

sin ðβÞ

5 0;

which is the Law of Refraction.

The Law of Refraction, published by Fermat in

February 1662, is known as Snell’s Law after Will-

ebrord van Snel van Roijen (15801626, Leiden), who

had discovered a graphical procedure for determining

the direction of a refracted ray. (Snel published his

papers using the Latin version, Snellius, of his name

and that accounts for the common spelling). Given the

blunders in Descartes’s “derivation” of Snell’s Law,

Fermat was astounded to ﬁnd himself reaching the

same conclusion. As he wrote to Clerselier

“The reward of my work has been the most extra-

ordinary, unexpected, and fortunate that I have ever

obtained. Because, after running through all the

equations, multiplications, antitheses, and other

operations of my method, and having ﬁnally brought

this problem to a conclusion [as enclosed], I found

that my principle gave precisely the same ratio of

refractions that M. Descartes had obtained. I was so

surprised by this unexpected event that I scarcely

recovered from my astonishment.”

Fermat’s Principle of Least Time was not accepted by

his contemporaries. Clerselier wrote to Fermat on 6

May 1662:

“The principle which you take as the basis of your

demonstration . . . is nothing but a moral principle

and not a physical one; it is not, and cannot be, the

cause of any effect of Nature.”

In Fermat’s last scientiﬁc letter, it is not known to

whom, he wrote “[the Cartesians] prefer to leave the

matter undecided . . . Let posterity be the judge.”

Rolle’s Theorem and The Mean Value

Theorem

Michel Rolle (1652, Ambert - 1719, Paris) published his

Trait

e d’Alge

bre in 1690. In a follow-up one year later,

Rolle demonstrated that if P (x) is a polynomial, then

(x) has a real root between any two real roots of

P (x). He did not, however, state his result, which we

now call Rolle’s Theorem, in the language of deriva-

tives. Instead, he used his “Method of Cascades,” a

formal algebraic operation on a polynomial P (x).

Indeed, Rolle was a vigorous opponent of inﬁnitesi mal

methods, which he did not be lieve to have a solid

foundation.

The Mean Value Theorem ﬁrst appeared (in geo-

metric form) in the Geometria Indivisibilibus Con-

tinuorum of 1635 of Bonaventura Cavalieri (1598 (?),

Milan1647, Bologna). Its analytic formulation is

sometimes attributed to Lagrange, sometimes to the

physicist Andr

e-Marie Ampe

re (1775, Lyon1836,

Marseille), who used it in a paper written in 1806.

The Newton-Raphson Method

Newton’s metho d of approximating real roots of poly-

nomials appeared in a paper of 1669 but the ﬁrst pub-

lished account appeared in Wallis’s Algebra of 1685.

Wallis demonstrated the technique with Newton’s

example: y

2 2y 2 5 5 0. Newton chose 2 as the ﬁrst

approximation to the root and substituted 2 1 p for y,

obtaining the equation p

1 6p

1 10p 2 1 5 0 for the

error p. By neglecting the terms involving p

and p

Newton solved p 5 0.1 1 q (where q is an error term).

He substituted the right side into the cubic polynomial

xd  x

m Figure 3

Genesis & Development 373

for p, obtaining q

1 6.3q

1 11.23q 1 0.061 5 0. He

carried out the next step in the same way, writing

q 520.061/11.23 1 r or q 520.0054 1 r. Newton con-

tinued with one more iteration, obtaining a term

s 520.00004854. The resulting approximation to the

root is 2 1 p 5 2 1 0.1 1 q 5 2 1 0.1 2 0.0054 1 r 5 2 1

0.1 2 0.0054 2 0.00004854 5 2.09455146, which agrees

with the exact root to 8 decimal places.

Notice that, in Newton’s original algorithm, the

function under consideration changes at every step.

Moreover, the derivative does not explicitly appear. In

a booklet that appeared in 1690, Joseph Raphson (1648

(?)1715 (?)) introduced the important modiﬁcations

that transformed Newton’s method into the easily

implemented form we now use. Raphson’s improve-

ment is that the function Φ(x) 5 x 2 f (x)/f

(x) that is

used remains the same at every step of the iteration.

374 Chapter 4 Applications of the Derivative