Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

CHAPTER 5

The Integral

Up to now, our discussion of calculus has been limited to the derivative and its

applications. In this chapter, we learn about one of the most powerful and perva-

sive tools in all of mathematical science: the deﬁnite integral of a function f. The

deﬁnite integral represents a limit of the form

lim

Δx-0



f ðx

ÞΔx þ f ðx

ÞΔx þþf ðx

ÞΔx



;

where Δx is an increment of x, as usual. Like the derivative, the deﬁnite integral

involves the key concept of calculus: the limit . However, addition and multi-

plication are the algebraic operations of the deﬁnite integral. This contrasts with

the deﬁnition of the derivative,

ðxÞ5 lim

Δx-0

f ðx 1 ΔxÞ2 f ðxÞ

Δx

;

which involves subtraction and division.

In Section 5.1, we motivate the deﬁnition of the integral by considering the

problem of calculating area. We learn that, if f is a positive function deﬁned on the

interval [a, b], then we can think of the deﬁnite integral as the area of the planar

region that lies under the graph of y 5 f (x), above the x-axis, and between the

vertical lines x 5 a and x 5 b. However, keep in mind that the integral is useful in

analyzing many different mathematical and physical problems. We begin with

area simply because it provides us with an accessible and geometrical place to start,

but area is only the ﬁrst of many interpretations of the deﬁnite integral that we

will learn.

The contrasting algebraic operations involved in the derivative and the integral

suggest that the processes of differentiation and integration are in some way inverse

to one another. The Fundamental Theorem of Calculus links the two main

branches of calculus by making the inverse relationship between derivative and

integral precise. In doing so, the theorem provides a rule that allows us to calculate

many deﬁnite integrals without referring to the limit deﬁnition. For deﬁnite inte-

grals that lie beyond the power of the Fundamental Theorem of Calculus, it is

important to have efﬁcient numerical approximation methods. In this chapter, we

study several of these numerical techniques as well.

PREVIEW

375

5.1 Introduction to Integration—The Area Problem

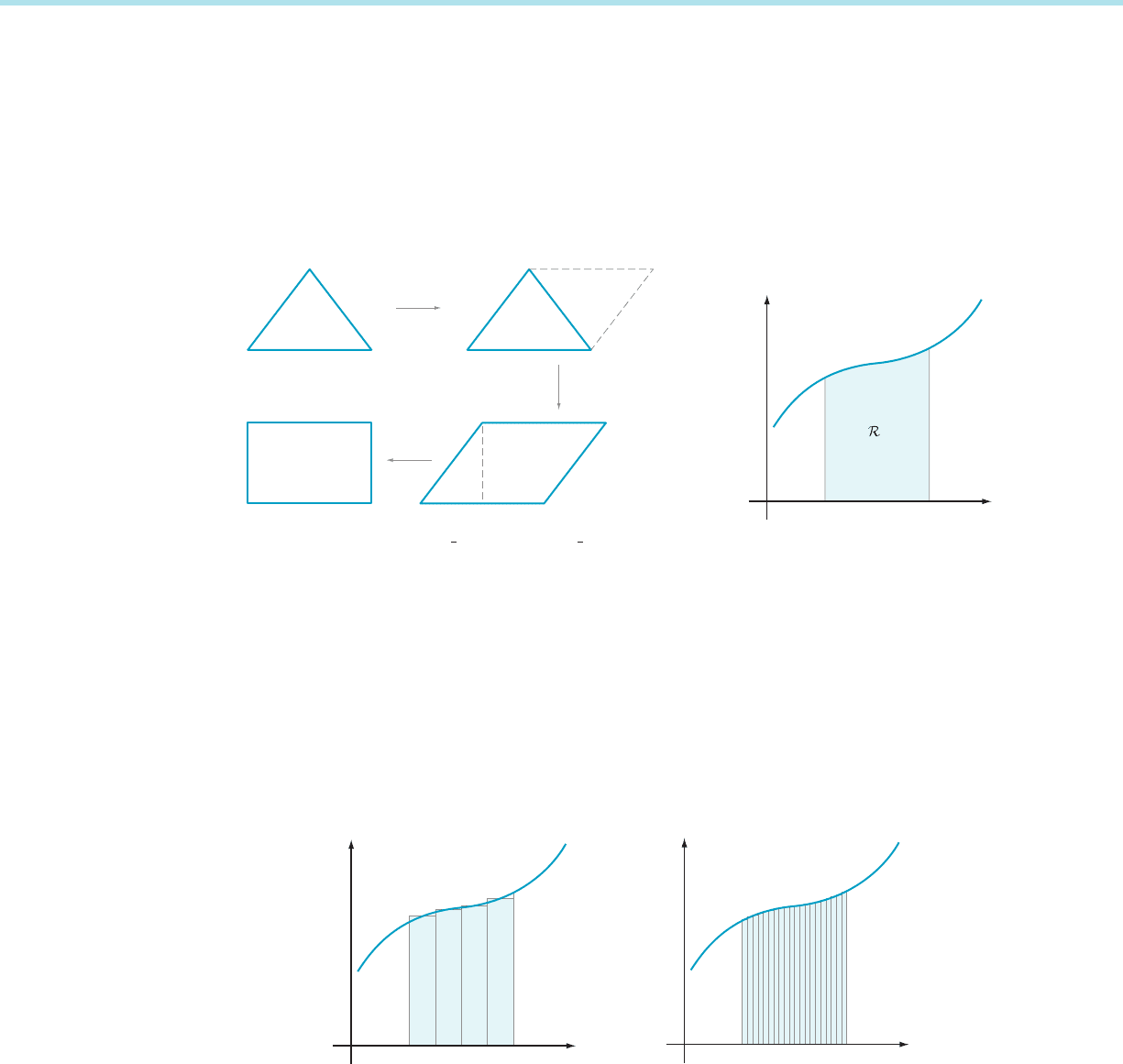
We calculate the area of a rectangle by multiplying length by width. We ﬁnd other

areas, such as the area of a trapezoid or of a triangle, by performing geometric

constructions to reduce the problem to the calculation of the area of a rectangle

(see Figure 1). If we wish to calculate the area of the region under the graph of a

funct

ion y 5 f (x), then there is no hope of dividing the region and reassembling it

into one rectangle (see Figure 2). Instead we attempt to divide the region into many

rectangles.

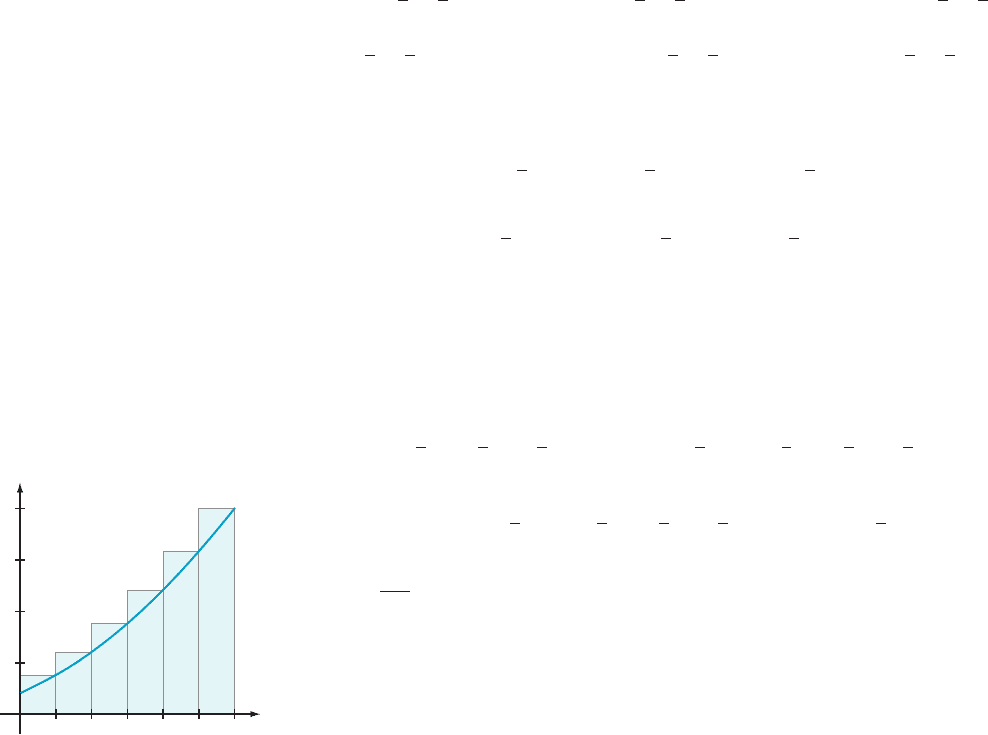
Figure 3 suggests the procedure that we will follow: The area of the shaded

regi

on is approximated by the sum of the areas of the rectangles. Of course, there is

some inaccuracy: Notice that the rectangles do not quite ﬁt. Parts of some of the

rectangles protrude from the region while other parts fall short. If we take a great

many rectangles, as in Figure 4, it appears that the sum total of all these errors is

quite small. We might hope that, as the number of rectangle s becomes ever larger,

the total error tends to zero. If so, this procedure would tell us the area of region

R in Figure 2.

EAC

m Figure 1 Area (ΔABC) 5

area (EBDF) 5

y  f(x)

m Figure 2

y  f(x)

m Figure 3

y  f(x)

m Figure 4

376 Chapter

5 The Integral

Approximating an area by subdividing into simple regions (rectangles or

triangles) is an ancient program. It is the method by which Archimedes obtained

the formula for the area inside a circle. This chapter presents the method precisel y.

Before we begin, however, it will be convenient to learn a notation for the sum of a

large or indeﬁnite number of terms.

Summation Notation If a

, a

, ...,a

is a (ﬁnite) sequence of numbers, then we denote the sum,

1 a

1 1 a

, of these numbers by

i5 1

. For example, if you turn in

eight assignments in a course and receive a

points for the ﬁrst assignment, a

points

for the second assignment, and so on, then your total homework score for the

course, a

1 a

, can be expressed concisely as

i5 1

In general, if M and N are integers with M # N and if a

, a

M11

, a

M12

, ...,a

are

numbers (or algebraic expressions), then we read the notation

i5 M

as “the sum

of the numbers (or algebraic expressions) a

for i equal to M, M 1 1, M 1 2, ...,up

to i equal to N.” Thus

i5 M

5 a

1 a

M11

1 a

M12

1 1 a

⁄ EX

AMPLE 1 Evaluate the sums

i5 1

and

i5 5

ð3i 1 4Þ.

Solution Th

e sum

i5 1

is a shorthand notation for 1

1 2

1 3

1 4

1 5

,which

equals 55. The expression

i5 5

ð3i 1 4Þ means (3 5 1 4) 1 (3 6 1 4) 1 (3 7 1 4) 1

(3 8 1 4), which equals 94.

The symbol Σ, which is the capital Greek letter “sigma,” stands for “summa-

tion.” A certain amount of ﬂexibility is inherent in the sigma notation. The sum can

begin at any integer M and can end at any integer N with N $ M. The letter i in the

sum

i5 M

is called the index of summation . Because the summation index i is

simply a placeholder for the integers from M to N, another letter could be used

with no change in meaning. Thus

i5 M

j5 M

Also, the distributive law and the associativity of addition can be used to manipulate

sums. Thus if a

, a

M11

,...,a

, b

M11

,...,b

, and are real numbers, then

i5 M

ða

1 b

Þ5

i5 M

ð5:1:1Þ

and

for any constant α

i5 M

α  a

5 α 

i5 M

ð5:1:2Þ

⁄ EX

AMPLE 2 Evaluate the sum

j5 1

ð3j

2 5jÞ.

Solution Using

(5.1.1) and (5.1.2), we calculate

j5 1

ð3j

2 5jÞ 5 3 

j5 1

2 5 

j5 1

5 3ð1

1 2

1 3

1 4

Þ2 5ð1 1 2 1 3 1 4Þ5 3  30 2 5  10 5 40: ¥

5.1 Introduction to Integration—The Area Problem 377

Some Special Sums Ther e are certain sums that we use frequently. For example, we have already

considered the sum 1 1 r 1 r

1  1 r

N21

, which arises when we add the terms of

the geometric sequence fr

N21

j5 0

with r 6¼1 (see Section 2.5 in Chapter 2). Using

sigma notation, we can express formula (2.5.2) for the sum of a geometric series as

N21

j5 0

2 1

r 2 1

ðr 6¼ 1Þ: ð5:1:3Þ

The following are two more sums that will be useful in this section. (Proofs of these

formulas are outlin ed in Exercises 5355.)

j5 1

j 5

NðN 1 1Þ

ð5:1:4Þ

j5 1

NðN 1 1Þð2N 1 1Þ

ð5:1:5Þ

⁄ EX

AMPLE 3 Use formulas (5.1.4) and (5.1.5) to calculate 1 1 2 1 3 1  1

100 and 100 1 121 1 144 1 169 1 1 400.

Solution By

formula (5.1.4),

1 1 2 1 3 1 

1 100 5

100

j5 1

j 5

100 ð100 1 1Þ

5 5050:

The second sum is equal to 10

1 11

1 12

1 13

1 1 20

. To apply formula

(5.1.5), which tells us how to evaluate the sum of consecutive squares when the ﬁrst

term is 1

, we must ﬁrst rewrite the given sum:

1 11

1 12

1 13

1 1 20

j5 10



j5 1



j5 1

20  21  41

9  10  19

5 2585: ¥

The sum in the next example is called a collapsin

g sum or telescoping sum.

⁄ EX

AMPLE 4 Suppose that x

, x

, ...,x

are points in the domain of a

function F. Show that

j5 1



Fðx

Þ2 Fðx

j21



5 Fðx

Þ2 Fðx

Þ: ð5:1:6Þ

Solution We

can see the pattern from the cases N 5 2 and N 5 3:

j5 1



Fðx

Þ2 Fðx

j21





Fðx

Þ2 Fðx





Fðx

Þ2 Fðx



5 Fðx

Þ2 Fðx

378 Chapter 5 The Integral

and

j5 1



Fðx

Þ2 Fðx

j21





Fðx

Þ2 Fðx





Fðx

Þ2 Fðx





Fðx

Þ2 Fðx



5 Fðx

Þ2 Fðx

Þ: ð5:1:7Þ

Notice that, in every pair of consecutive summan ds, the second term of the second

summand cancels with the ﬁrst term of the ﬁrst summand. For example, look at the

second summand, (F (x

) 2 F (x

)), on the right side of equation (5.1.7). Observe

that the term F (x

) cancels with the term 2F(x

) of the succeeding summand, and

the term 2F(x

) cancels with the term F(x

) of the preceding summand. When all

the cancellations are performed, the only terms that remain are 2F (x

), which does

not have a predecessor with which to cancel, and F(x

), which does not have a

successor with which to cancel.

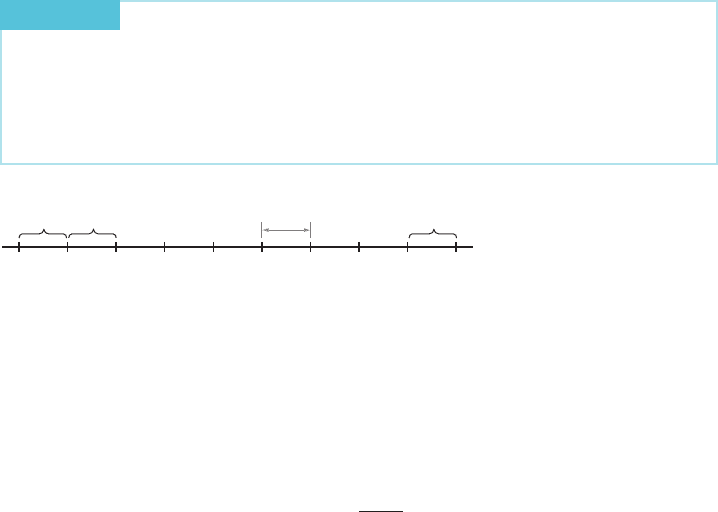
Approximation of Area Let f be a positive, continuous function deﬁn ed on an interval [ a , b]. Let R be the

region lying above the x-axis, below the graph of the function y 5 f (x), and between

the vertical lines x 5 a and x 5 b, as shown earlier in Figure 2. Our goal is to

determi

ne the area of R. As a ﬁrst step, we will approximate R by rect angles. The

terminology and notation we now introduce will describe and denote the bases of

the approximating rectangles.

DEFINITION

Let N be a positive integer. The uniform partition P of order N of

the interval [a, b] is the set fx

, x

, ...,x

g of N 1 1 equally spaced points such

that

a 5 x

, x

, , x

N21

, x

5 b:

See Figure 5.

If P is a uniform partition of order N of [a, b], then the points of P divide [a, b]

into N subintervals,

5 ½x

; x

; I

5 ½x

; x

;:::;I

5 ½x

N21

; x

;

of equal length Δx, where

Δx 5

b 2 a

: ð5:1:8Þ

Refer again to Figure 5. Notice that each point x

of P with j $ 1 can be obtained

from the preceding point x

j21

by adding Δx:

5 x

j21

1 Δx ð1 # j # NÞ: ð5:1:9Þ

a  x

j1

 b

x

m Figure 5 In the uniform partition of order N of the interval [a, b], each subinterval has

width Δx 5 (b 2 a)/N.

5.1 Introduction to Integration—The Area Problem 379

Formula (5.1.9) is convenient for successively calculating the points of P. Alter-

natively, each point x

of P can be expressed in terms of its distance j Δx from a:

5 a 1 j  Δx ð0 # j # NÞ: ð5:1:10Þ

To approximate the area of region R of Figure 2, we choose a positive integer

N and

erect a rectangle over each of the subintervals I

, I

,...,I

that arise from

the uniform partition of order N. How tall should each rectangle be? We want each

rectangle to be tall enough to touch the graph. One convenient way to achieve this

is to take the height of the jth rectangle—that is, the rectangle that has subinterval

5 [x

j21

, x

] as its base—to be f (x

), as shown in Figure 6. Thus the jth rectangle

(shaded most darkly in Figure 6) has height equal to f (x

), base equal to Δx, and

area equal to the product f (x

) Δx of the height and the base. The sum of all the

rectangular areas,

j5 1

f ðx

ÞΔx; ð5: 1 :11Þ

is said to be a right endpoint approximation of the area of the region bounded

above by the curve y 5 f (x), below by the x-axis, and on the left and right by the

vertical lines x 5 a and x 5 b.

⁄ EX

AMPLE 5 Using the uniform partition of order 6 of the interval [1, 4],

ﬁnd the right endpoint approximation to the area A of the region bounded

above by the graph of f (x) 5 x

1 x, below by the x-axis, on the left by the vertical

line x 5 1, and on the right by the vertical line x 5 4.

Solution Makin

g the correspondence between the given data and the general

notation used in formula (5.1.11), we have a 5 1, b 5 4, N 5 6, and Δx 5 (b 2 a)/N

y  f(x)

j1

f(x

)

m Figure 6 The height of the jth rectangle f (x)

380 Chapter 5 The Integral

5 (4 2 1)/6 5 1/2. The ﬁrst point of the speciﬁed partition is x

5 a 5 1, and then we

calculate successively

5 x

1 Δx 5 1 1

; x

5 x

1 Δx 5

5 2; x

5 x

1 Δx 5 2 1

;

5 x

1 Δx 5

5 3; x

5 x

1 Δx 5 3 1

; x

5 x

1 Δx 5

5 4:

These points divide the interval [1, 4] into these six subintervals:





; I



; 2



; I





;



; 3



; I





; I



; 4



Each subinterval is the base of a rect angle that is used in the approximation.

Formula (5.1.11) gives us the right endpoint approximation:

j5 1

f ðx

ÞΔx 5 f ðx

ÞΔx 1 f ðx

ÞΔx













1 2





















1 3





















1 4









265

5 33:125:

This quantity, the sum of the areas of the shaded rectangles shown in Figure 7, is

the

requested approximation of A. Figure 7 shows that this estimate is not very

accurate (as is to be expected when Δx is not very small). Exercise 46 asks you to

show that A 5 57/2 (exactly) using techniques that are developed in Examples 6

and 7 of this section.

A Precise Deﬁnition

of Area

Figures 3 and 4, shown earlier, suggest that, as N gets larger, the sums in formula

(5.1.11) tend to approximate the area of the region under the graph of f more and

more accurately. Actually, that area is not yet a deﬁned concept. Our primitive

notion of area allows us to compare the areas of different regions—to say that one

region has greater area than another or that two regions have equal areas or nearly

equal areas. However, our intuition does not help us assign numerical values to

the areas of curved regions. To do that, we approximate the region by rectangles,

sum the area of those rectangles, as in formula (5.1.11), and take the limit of

these sums as the common length of the bases of the approximating rectangles

decreases to 0.

3.52.01.5 2.5 3.0 4.0

y  x

 x

m Figure 7

5.1 Introduction to Integration—The Area Problem 381

DEFINITION

The area A of the region that is bounded above by the graph of f,

below by the x-axis, and laterally by the vertical lines x 5 a and x 5 b, is deﬁned

as the limit

A 5 lim

N-N

j5 1

f ðx

ÞΔx: ð5 :1:12Þ

As deﬁned in Section 2.5, this means that, for every ε . 0, we can force the area

of the rectangular approximation, namely

j5 1

f ðx

ÞΔx, to be within ε of the

quantity A by taking a sufﬁciently large number N of rectangles.

INSIGHT

Suppose that we did not deﬁne the area to be this exotic-looking limit.

What would the area of a region bounded by curves mean? The answer is that it would

not mean anything—there would be no prior deﬁnition for this concept. If we wish to

consider area, we must ﬁrst deﬁne the concept. Having done so, we must show that our

intuitive ideas about area are consistent with the deﬁnition we have adopted.

Granted that some deﬁnition is needed, we may still question the particular deﬁnition

adopted. Does limit (5.1.12) exist? Yes, for continuous functions, it does exist. Would the

limit be different if we had determined the height of the rectangle with base I

5 [x

j21

, x

]

by using some point in I

other than the right endpoint x

? No, the limit would be the

same. The left endpoint, the midpoint, or any other point of I

would serve just as well in

limit (5.1.12). We discuss these issues in greater detail in Section 5.2.

We now use this deﬁnition of the area concept to calculate some areas.

⁄ EX

AMPLE 6 Calculate the area A of the region that is bounded above by

the graph of y 5 2x, below by the x-axis, and on the sides by the vertical lines x 5 0

and x 5 6.

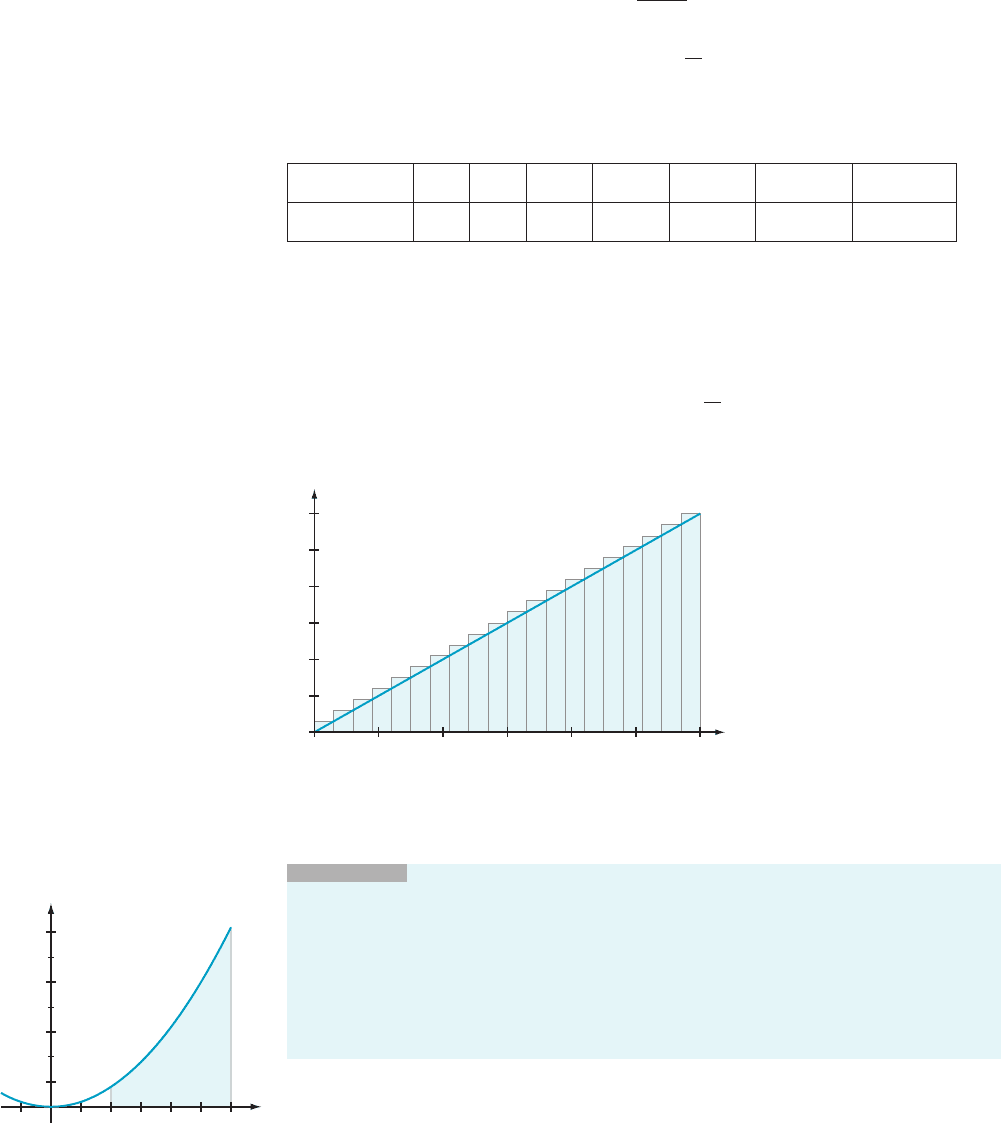
Solution In

this example, we take a 5 0, b 5 6, and f (x) 5 2x . When we divide the

interval [0, 6] into N equal subintervals, the common length is Δx 5 (6 2 0)/N 5

6/N. The points of the uniform partition of order N are, by formula (5.1.10),

5 a 1 j  Δx 5 0 1 j 

ð0 # j # NÞ :

The next step is to simplify the sum that appears on the right side of deﬁnition

(5.1.12). We calculate

j5 1

f ðx

ÞΔx 5

j5 1







j5 1

2 



j5 1



NðN 1 1Þ

ð5:1:4Þ

382 Chapter 5 The Integral

5 36

N 1 1

5 36



1 1



The values of this expression are tabulated for seven choices of N:

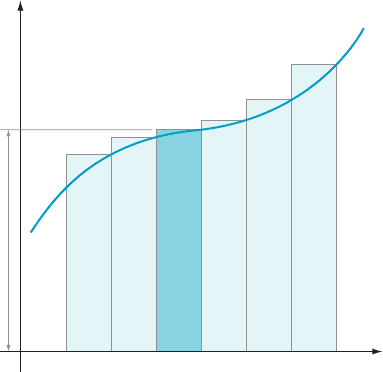
N 10

20 100 1000 10 000 100 000 1 000 000

36 (1 1 1/N) 39.6 37.8 36.36 36.036 36.0036 36.00036 36.000036

Figure 8 shows the approximation for N 5 20.

The area of the region inside the 20

approximating rectangles is, according to the table, 37.8. Moving to the right along

the second row of the table, we see that the approximations become closer to 36 as

N increases. We calculate the exact area using deﬁnition (5.1.12):

A 5 lim

N-N

j5 1

f ðx

ÞΔx 5 lim

N-N



1 1



5 36ð1 1 0Þ5 36: ¥

INSIGHT

The test of any new concept is twofold: Is it consistent with simpler

concepts when those simpler concepts are applicable? Does it succeed in any cases for

which the simpler concepts fail? In Example 6, the region for which we calculated area is

a right triangle with base 6 and altitude 12. The familiar formula for the area of a triangle,

half the base times the height, tells us that, for the triangular region of Example 6, A 5

(1/2)(6)(12), or A 5 36. Thus our new deﬁnition of area agrees with the standard deﬁ-

nition in this example. In the next example, we use limit (5.1.12) to evaluate an area that

requires the limit concept.

⁄ EXAMPLE 7 Calculate the area A of the region (shaded in Figure 9) that is

under the graph of f (x) 5 x

, above the x-axis, and between the vertical lines x 5 2

and x 5 6.

123

Area a

roximation for N  20

y  2x

456

m Figure 8

511 2 3 4

y  x

m Figure 9

5.1 Introduction to Integration—The Area Problem 383

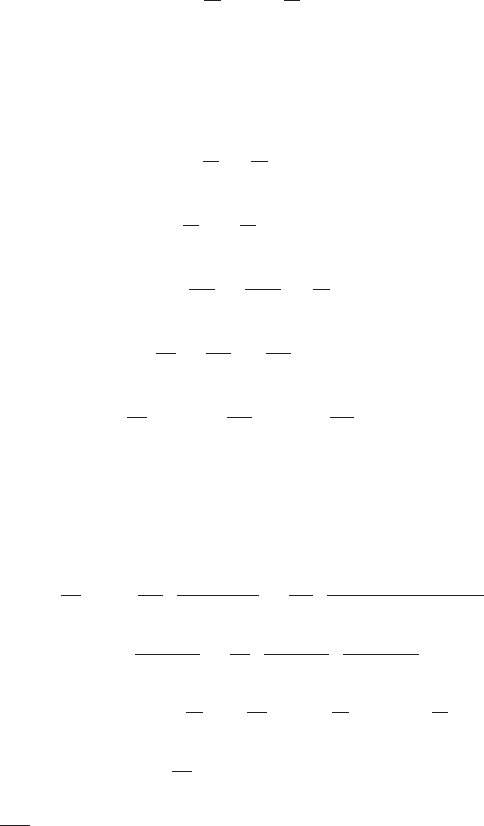
Solution Here a 5 2, and b 5 6. We divide the interval [2, 6] into N subintervals of

equal length Δx 5 (b 2 a)/N 5 (6 2 2)/N 5 4/N by means of the uniform partition

with points

5 a 1 j  Δx 5 2 1 j 

5 2 1

ð0 # j # NÞ :

Using deﬁnition (5.1.12) for the area, we calculate

A 5 lim

N-N

j5 1

f ðx

ÞΔx

5 lim

N-N

j5 1



2 1





5 lim

N-N

j5 1







5 lim

N-N

j5 1



4 1

16j





5 lim

N-N

j5 1



j 1



5 lim

N-N





j5 1

1 1



j5 1

j 1



j5 1



The ﬁrst sum on the right side is 1 þ 1 þþ1

|ﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ}

Nterms

,orN. Formulas (5.1.4) and (5.1.5)

give us the values of the other two sums. When we replace these three sums with

their values, we obtain

A 5 lim

N-N



 N 1



NðN 1 1Þ



NðN 1 1Þð2N 1 1Þ



5 lim

N-N



16 1 32 

ðN 1 1Þ



ðN 1 1Þ



ð2N 1 1Þ



5 lim

N-N



16 1 32 



1 1







1 1







2 1



5 lim

N-N



16 1 32  1 1

 1  2



208

: ¥

Concluding Remarks The method that we have used to deﬁne area can be used to attack many different

types of problems in addition to the calculation of area. For example, later in this

chapter, we will apply the ideas of this section to analyze income distribution and

compute cardiac output. In Chapter 7, we will see that the right side of equation

(5.1.12) can be used to calculate other geometric quantities such as volume, arc

length, and surface area, as well as physical quantities such as work and center of

mass. In the rest of the present chapter, we develop a general tool, called the

Riemann integral, that enables us to study all of these types of problems. We also

384 Chapter 5 The Integral