Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

investigate a method of evaluating Riemann integrals that does not require the

elaborate and tedious algebra used to solve Example 7.

QUICK QUIZ

1. Calculate

j5 0

cosðjπ=4 Þ.

2. Calculate

j5 0

ð2j 1 j

1 2

Þ.

3. What is the ﬁfth subinterval of [3, 9] when the uniform partition of order 7 is

used?

4. What is the right endpoint approximation of the area of the region under the graph

of y 5 1/x and over the interval [1, 2] when the uniform partition of order 3 is used?

Answers

1. 1 2. 41 3. [45/7, 51 /7] 4. 37/60

EXERCISES

Problems for Practice

c In Exercises 1210, write out the sum, and perform the

addition. b

j5 1

j5 0

ð2j 2 1Þ

j5 2

ð22j

‘5 4

‘=ð‘ 2 3Þ

n5 2

2n=ðn 2 1Þ

k5 2

ðk

2 6kÞ

m5 3

ð2m

2 3mÞ

j5 1

j  sinðjπ=2Þ

j5 1

j  sin

ðjπ=6Þ

10.

j5 0

1=ð2j 2 3Þ

c In Exercises 11216, use summation notation to express

the

sum. b

11. 2 1 3 1 4 1 5 1 6

12. 3 1 6 1 9 1 12 1 15

13. 9 1 13 1 17 1 21 1 25 1 29

14. 9 1 16 1 25 1 36

15. 1/4 1 1/5 1 1/6 1 1/7 1 1/8

16. 2/5 1 3/7 1 4/9 1 5/11

c Use formulas (5.1.4) and (5.1.5) to calculate the sums in

Exercises 17222. b

17.

j5 1

18.

j5 1

ðj

2 4Þ

19.

j5 1

ðj

1 2jÞ

20.

j5 1

ð3j

1 2j 1 1Þ

21.

j5 12

ð3j 2 2Þ

22.

j5 7

ð2j

2 21jÞ

c In Exercises 23226, use an identity to simplify the sum. b

23.

j5 0

expðjÞ

24.

j5 0

2j21

j11

25.

j5 2

lnðjÞ

26.

j5 7



j 1 1



c In each of Exercises 27238, calculate the right endpoint

approximation

of the area of the region that lies below the

graph of the given function f and above the given interval I of

the x-axis. Use the uniform partition of given order N. b

27. f (x) 5 x

2 2xI5 [3, 5], N 5 2

28. f (x) 5 1/xI5 [2, 3], N 5 2

29. f (x) 52log

(x) I 5 [1/2, 1], N 5 2

30. f (x) 5 2x

1 1 I 5 [0, 9/2], N 5 3

31. f (x) 5 2 1 sin (2x) I 5 [π/2, 2π], N 5 3

32. f (x) 5 4 2 3 cos (x) I 5 [0, 4π], N 5 3

33. f (x) 5 x/(x 1 1) I 5 [24, 22], N 5 4

34. f (x) 5 2x/(2x 2 1) I 5 [23, 21], N 5 4

35. f (x) 5 x sin (x) I 5 [2π, π], N 5 4

36. f (x) 5 sec

(x) I 5 [2π/3, π/3], N 5 4

37. f (x) 5 x

2 6x 1 6 I 5 [21, 5/2], N 5 7

38. f (x) 5 x 1 cos (2x) I 5 [0, 3π], N 5 6

Further Theory and Practice

c Suppose that f (x) $ 0 for x in I 5 [a, b]. If for each sub-

interval [x

j21

, x

] that arises from the uniform partition

P 5 fx

, x

, ...,x

g of I, we use the left endpoint x

j21

instead

5.1 Introduction to Integration—The Area Problem 385

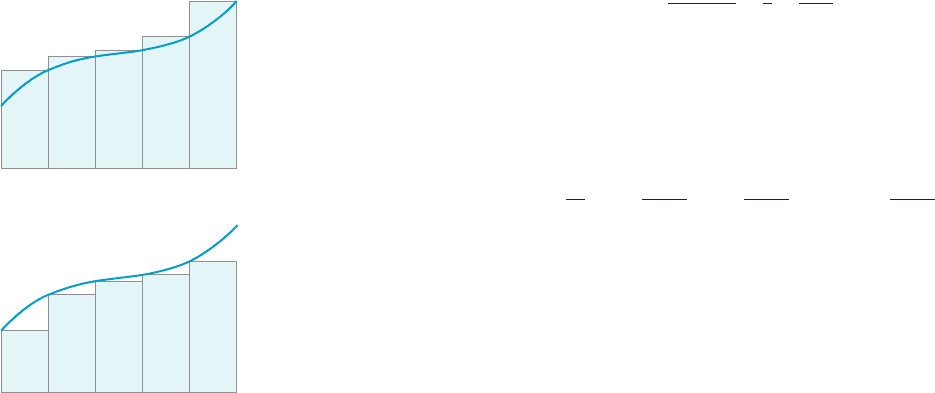
of the right endpoint in formula (5.1.9), then we obtain the

left endpoint approximation

j5 1

f ðx

j21

ÞΔx

of the area A of the region below the graph of f and above I (see

Figure 10). As can be seen from Figure10, if f in

creases on I,then

the right endpoint approximation overestimates A, and the left

endpoint approximation underestimates A. In each of Exercises

39244, calculate the average of the left and right endpoint

pproximations. (For purposes of comparison, the exact value of

A is given. Notice that your answer is more accurate than both

the left and right endpoint approximations.) b

39. f (x) 5 sin

(x) I 5 [0, π/3], N 5 2, A 5 1/2

40. f (x) 5 2 1 tan (x) I 5 [2π/4, π/4], N 5 2, A 5 π

41. f (x) 5 (2x 1 1)/(x 1 1) I 5 [0, 2], N 5 2, A 5 4 2 ln(3)

42. f (x) 5 1 1 x

I 5 [21, 3], N 5 3, A 5 24

43. f (x) 5 1 2 1/x

I 5 [1, 2], N 5 3, A 5 1/2

44. f (x) 5 16

I 5 [0, 1], N 5 4, A 5 15/ln(16)

45. Following the technique from Example 7, calculate the

area of the region that lies below the graph of f (x) 5

4 2 x

and above the interval [0, 2] of the x-axis.

46. Following the technique from Examples 6 and 7, show that

the area of the region that lies below the graph of f (x) 5

1 x and above the interval [1, 4] of the x-axis is 57/2.

47. Find p such that e

5 e e

e

...e

100

. Find q so that

lnðqÞ5

100

n5 1

lnðnÞ.

48. Calculate the sum S 5

j5 1

ð2j 2 1Þ of the ﬁrst N odd

positive integers.

49. Calculate the sum S 5

j5 1

ð2jÞ

of the ﬁrst N even

positive square integers. Subtract your value of S from the

value of

j5 1

to calculate the sum

j5 1

ð2j2 1Þ

of the

ﬁrst N odd positive square integers.

50. Which is larger,

j5 1

j? Explain why.

51. Suppose that fa

j5 0

is a sequence of real numbers.

Suppose that M and N are integers such that 0 , M , N.

Show that

j5 M

ða

2 a

j21

Þ5 a

2 a

M21

Hint: Look at the cases N 5 M 1 1 and N 5 M 1 2to

determine the pattern.

52. Evaluate 1/2 1 1/6 1 1/12 1 1 1/(1000 1001) by writ-

ing the j th term as

j ðj 1 1Þ

j 1 1

and using Exercise 51.

53. Write

S 5 1 1 2 1 3 1 1 N

forward and backward:

S 5 1 1 2 1 1 N

S 5 N 1 N 2 1 1 1 1:

2S 5 N 1 1 1 N 1 1 1 1 N 1 1

Add vertically. Derive formula (5.1.4) by solving for S.

54. Derive formula (5.1.4) by noticing that

j5 1

ð2j 2 1Þ5

j5 1

ðj

2 ðj 2 1Þ

Þ:

Write the sum on the left in terms of S 5 1 1

2 1 3 1 1 N. Evaluate the sum on the right using

Exercise 51. Solve for S.

55. Derive formula (5.1.5) by noticing that

j5 1

ð3j

2 3j 1 1Þ5

j5 1

ðj

2 ðj 2 1Þ

Þ:

Write the expression on the left as a combination of three

sums, one of which is 3S 5 3(1

1 2

1 3

1 1 N

). Use

formula (5.1.4) to evaluate

j5 1

3j. Evaluate the sum on

the right using Exercise 51. Solve for S.

56. Suppose that b . 0. Following the technique from Example

6, show that the area of the region that lies below the graph

of f (x) 5 x

and above the interval [0, b]ofthex-axis is b

/3.

57. Let f (x) 5 x

. Suppose that b . 0 and that F (x)isan

antiderivative of f (x). In this exercise, we will approximate

the area A of the region that lies below the graph of f and

above the interval I 5 [0, b]ofthex-axis. We will use one

rectangle with base I. For the height, we use f (c)wherec is

the point in (0, b) obtained by applying the Mean Value

Theorem to F on I—see Figure 11. Use Exercise 56 to

ow that this approximation is, in fact, exact.

Right endpoint approximation

j1

Left endpoint approximation

m Figure 10

386 Chapter

5 The Integral

58. Show that

j5 1

ð4j

2 6j

1 4j 2 1Þ5

j5 1

ðj

2 ðj2 1Þ

Þ:

Evaluate the sum on the right using Exercise 51. Write

the expression on the left as a combination of four sums,

one of which is 4S 5 3(1

1 2

1 3

1 1 N

). Use for-

mula (5.1.4) to evaluate

j5 1

4j. Use formula (5.1.5) to

evaluate

j5 1

. Solve for S to obtain the identity

j5 1



NðN11Þ



59. Suppose 0 # a , b. Following the technique of Example 7,

use the formula from Exercise 58 to show that the area

under the curve y 5 xy5 x

from x 5 0tox 5 b is b

/4.

Deduce that the area under the curve y 5 x

from x 5 a to

x 5 b is (b

2 a

)/4.

60. Suppose m and k are positive constants. For f (x) 5

mx 1 k, let A (b) denote the area under the graph of f,

above the x-axis, and between x 5 0 and x 5 b. Calculate

A (b), and show that A

(b) 5 f (b).

61. For f (x) 5 x

, let A(b) denote the area under the graph of

f, above the x-axis, and between x 5 0 and x 5 b. Show

that A

(b) 5 f (b).

62. Notice that, in limit (5.4), lim

N-N

Δx 5 0. It may seem

that lim

N-N

j5 1

f ðx

ÞΔx 5 0 in view of the following

calculation:

lim

N-N

j5 1

f ðx

ÞΔx 5 lim

N-N

j5 1

f ðx

Þ lim

N-N

Δx



lim

N-N

j5 1

f ðx



 0

5 0:

Explain what is wrong with this reasoning.

63. For any positive integer k, let

ðkÞ5 1

1 2

1 3

1 1 N

It is known that

ðkÞ5

k 1 1

k11

1 P

ðNÞ

where P

is a polynomial of degree k. Accept this fact

without proof (but notice that for k 5 1, 2, and 3, this

assertion follows from formula (5.1.4), formula (5.1.5),

and Exercise 58, respectively).

a. Show that lim

N-N

(k)/N

k11

5 1/(k 1 1).

b. Suppose 0 # a , b. Show that the area under the curve

y 5 x

from x 5 0tox 5 b is b

k11

/(k 1 1).

c. Deduce that the area under the curve y 5 x

from x 5 a

to x 5 b is (b

k11

2 a

k11

)/(k 1 1).

64. Calculate lim

N-N

ð1=NÞ

j5 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 ðj=NÞ

by identifying

this number as the limit of right endpoint approximations

of the area of a region with known area.

65. Let f :[0,a] - [0, b] be a continuous, increasing, onto func-

tion. Let A denote the area in the xy-plane that liesunder the

graph of y 5 f (x) and above the interval [0, a] of the x-axis.

What is the area in the yx-plane that lies under the graph of

x 5 f

2 1

( y) and above the interval [0, b]ofthey-axis?

66. Use Exercise 51 and the product formula

sinðAÞcosðBÞ5



sinðA 1 BÞ1 sinðA 2 BÞ



with A 5 t/2 and B 5 kt to show that

k5 1

sin





cosðktÞ5



sin



N 1



2 sin





Use this summation formula, together with the product

formula, with A 1 B 5 (N 1 1/2)t and A 2 B 52t/2 to

show that

k5 1

cosðktÞ5

sinðNt=2ÞcosððN 1 1Þt=2Þ

sinðt=2Þ

67. Suppose 0 , b # π /2. Use the last formula from Exercise 66

with t 5 b/N to show that the area of the region under

the graph of y 5 cos (x) and over the interval [0, b]

is sin (b).

Calculator/Computer Exercises

c In a computer algebra system, a right endpoint approxima-

tion can be implemented by means of a one-line command. For

example, if the real numbers a and b, the positive integer N, and

the function f, have been deﬁned, then the command

evalfððbaÞ=N*addðfða1j*ðb2aÞ=NÞ; j51:: NÞÞ;

calculates formula (5.1.9) in Maple. In Exercises 68271,an

interval

[a, b], and a function f are given. The function is positive

y  f(c)

y  x

 C

(c)

y  x

m Figure 11

5.1 Introduction to Integration—The Area Problem 387

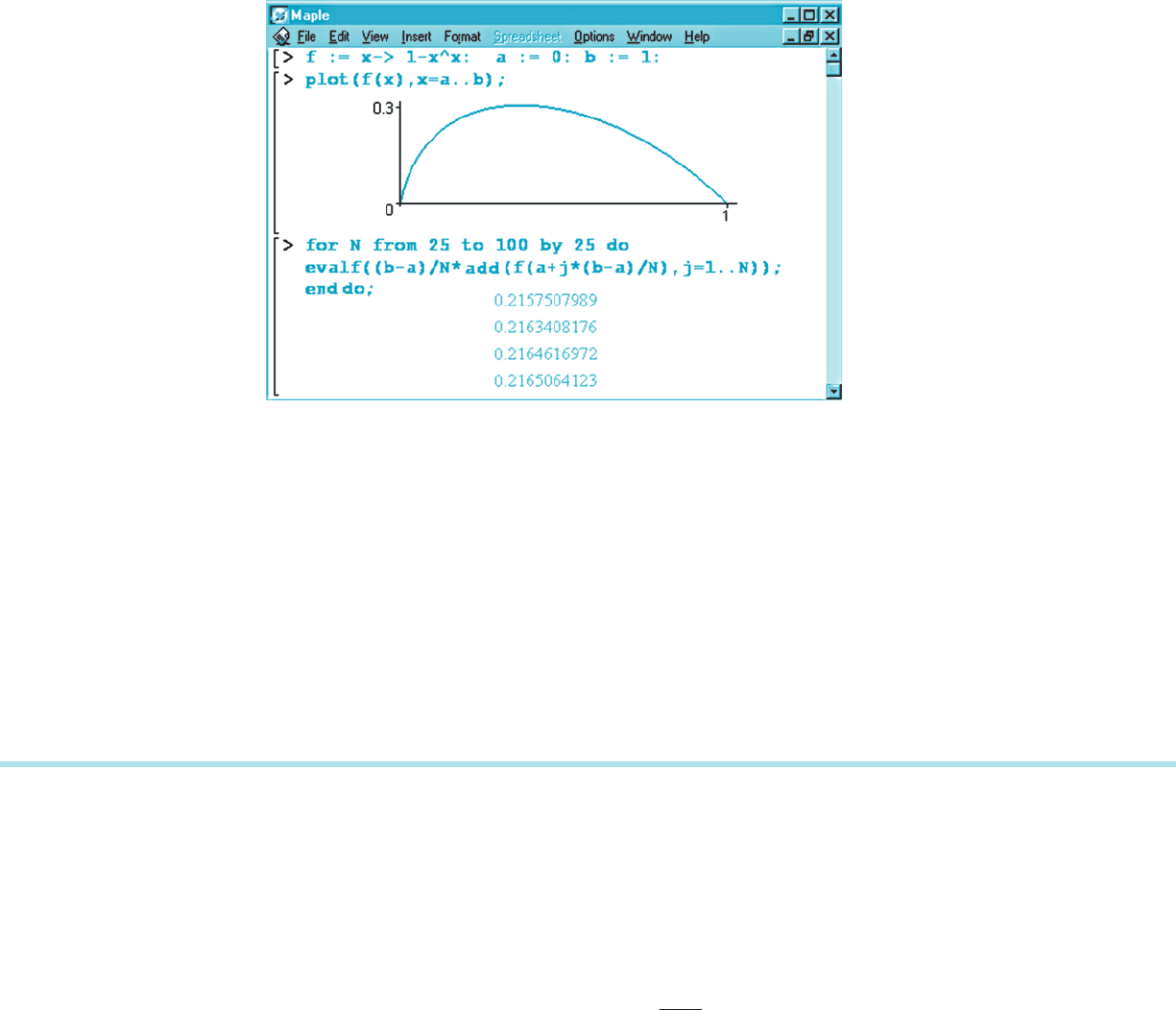
m Figure 12

on (a, b) and it is 0 at the endpoints. Approximate the area

under y 5 f (x) and over the interval [a, b] by using the right

endpoint approximation, starting with N 5 25. Increment N by

25 until the ﬁrst two decimal places of the sum remain the same

for three consecutive calculations. Figure 12 shows a Maple

implementation for the function f (x) 5 1 2 x

,0# x # 1. (This

procedure does not guarantee two decimal places of accuracy.

Section 5.7 presents several methods that can be used to achieve

a prescribed accuracy.) b

68. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

16 2 x

; 22 # x # 2

69. f ðxÞ5

ﬃﬃﬃ

2 x; 0 # x # 1

70. f ðxÞ5 ð2 2 x

Þ=ð2 1 x

Þ; 2

ﬃﬃﬃ

# x #

ﬃﬃﬃ

71. f ðxÞ5 sin

ðxÞ; 0 # x # π

c In each of Exercises 72275, locate the left x-intercept a

and

the right x-intercept b of the graph of the given function f.

Then follow the instructions for Exercises 68271. b

72. f ðxÞ5 1 1 2x 2 x

73. f ðxÞ5 2 1 x 2 exp ðxÞ

74. f ðxÞ5 10 2 x

2 1=x

75. f ðxÞ5 xexpð2x

Þ2 0:1

5.2 The Riemann Integral

We now deﬁne a mathematical operation on functions that captures the essence of the

method from Section 5.1, but that can be applied to several other situations as well.

Riemann Sums Let f be any function deﬁned on the interval [a, b]. (We no longer assume that f is a

nonnegative function.) Let N be a positive integer. As in Section 5, the uniform

partition of order N of the interval [a, b] is the set of N 1 1 equally spaced points

5 a 1 j 

b 2 a

ð0 # j # NÞ

that divides [a, b] into the N subintervals

5 ½x

; x

; I

5 ½x

; x

; :::; I

5 ½x

N21

; x



of equal length

388 Chapter 5 The Integral

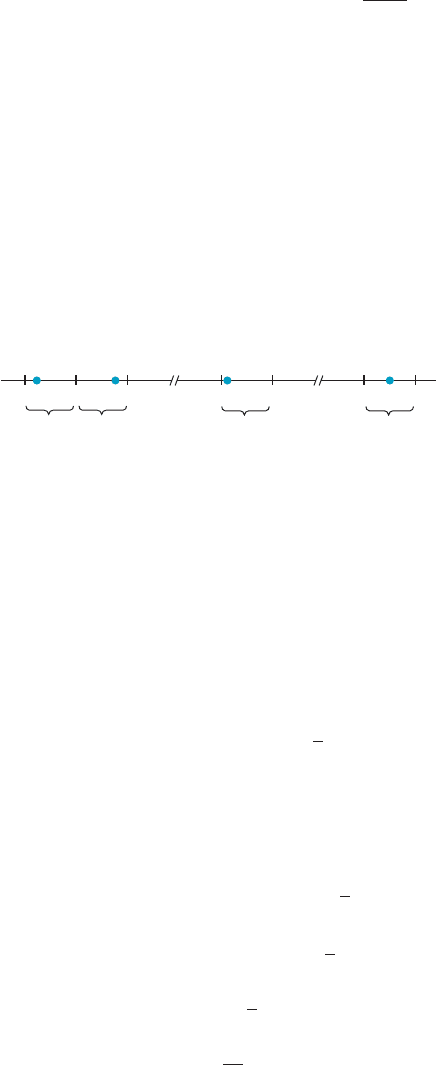
Δx 5

b 2 a

A choice of points S

associated with the uniform partition of order N is a sequence

, s

, ..., s

of points with s

in I

for each j. The point s

can be chosen arbitrarily

from the subinterval I

. Thus s

can be a right endpoint or a left endpoint or any

interior point. Figure 1 illustrates one possible choice of points. If S

is a choice of

points, then the expression

Rðf ; S

Þ5

j5 1

f ðs

ÞΔx ð5:2:1Þ

is called a Riemann sum of f. The notation R( f, S

) indicates that a Riemann sum

depends on the function f and the choice of points S

⁄ EX

AMPLE 1 Write a Riemann sum for the function f ( x ) 5 x

2 4 and the

interval [a, b] 5 [25, 3] using the partition f25, 23, 21, 1, 3g.

Solution Obser

ve that

5 ½25; 23; I

5 ½23; 21; I

5 ½21; 1 ; I

5 ½1; 3;

and Δx 5 2. To form a Riemann sum, we must ﬁrst make a selection of points s

(1 # j

# 4) with s

in I

. According to the deﬁnition, we may select any point s

in I

, any

point s

in I

, and so on. Here is our arbitrary choice:

523 2 I

; s

2 I

; s

5 0 2 I

; s

5 1 2 I

The Riemann sum for this collection of points S

Rðf ; SÞ 5

j5 1

f ðs

ÞΔx

5 f ð23Þ2 1 f





 2 1 f ð0Þ2 1 f ð1Þ2

5 ð9 2 4Þ2 1



2 4



 2 1 ð0 2 4Þ2 1 ð1 2 4Þ2

5 10 2

2 8 2 6

Of course, a different choice of points s

, s

would lead to a different Rie-

mann sum.

. . . . . .

j1

N1

m Figure 1

5.2 The Riemann Integral 389

INSIGHT

Example 1 shows that a Riemann sum can be negative. If we must give

this Riemann sum a geometric meaning, then we can think of it as a difference of areas,

namely,

Rðf ; S

Þ5 10

|{z}

Area of rectangle

above x-axis



1 8 1 6



|ﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ{zﬄﬄﬄﬄﬄﬄﬄﬄﬄﬄ}

Area of rectangles

below x-axis

See Figure 2. In later chapters, we will use Riemann sums to represent physical

quantities other than area. In those cases, it is usually not appropriate to associate

Riemann sums with the area concept.

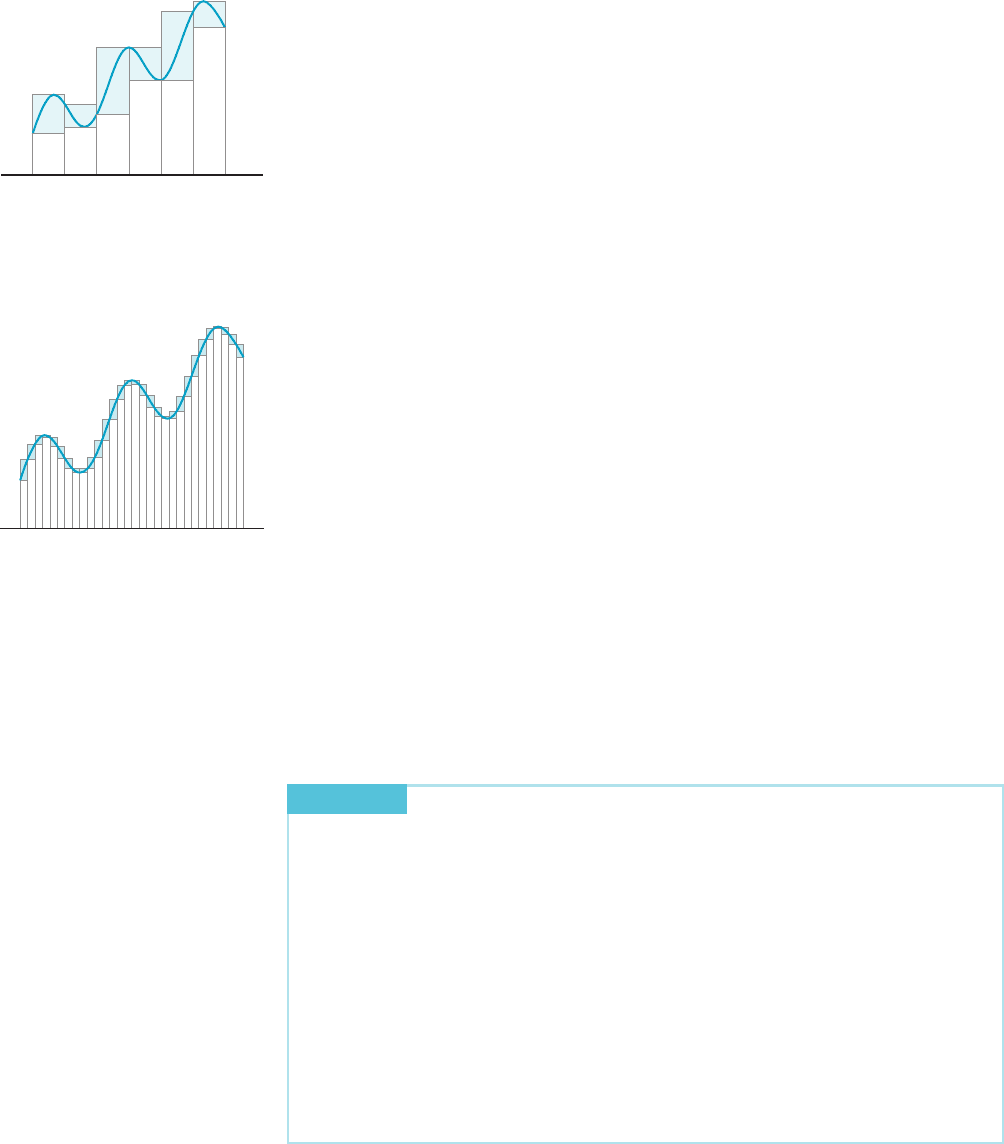
Suppose that f is continuous. Let ‘

be a point in I

at which f attains its

minimum value on I

(see Figure 3a), and let u

be a point in I

at which f achieves its

maximum value on I

(see Figure 3b). The Extreme Value Theorem (Section 2.3, in

Chapter 3) guarantees that such points ‘

and u

exist. We denote the resulting

choices of points associated to the uniform partition by L

5 f‘

, ‘

, ...,‘

g and

5 fu

, u

, ...,u

g. The Riemann sums

Rðf ; L

Þ5

j5 1

f ð‘

ÞΔx

and

Rðf ; U

Þ5

j5 1

f ðu

ÞΔx

are respectively called the lower Riemann sum and upper Riemann sum of order N.

They are the least and greatest Riemann sums of order N, as we will prove in

Theorem 1. Figures 4 and 5 illustrate typical lower and upper Riemann sums.

⁄ EX

AMPLE 2 Consider the continuous function f ( x ) 5 x

2 4 on the

interval [25, 3] (as in Example 1). Find the upper and lower Riemann sums of

order 4.

Solution The

four equal-length subintervals of [25, 3] are I

5 [25, 23],

5 [23, 21], I

5 [21, 1], and I

5 [1, 3]. The graph of f is shown in Figure 6, in

which the four subintervals have been separated. By inspection, f attains its

35 3

m Figure 2

f(ᐉ

)

j1

ᐉ

m Figure 3a

f(u

)

j1

m Figure 3b

 bx

j1

a  x

m Figure 4 The area of the

shaded rectangles is a lower

Riemann sum.

 bx

j1

a  x

m Figure 5 The area of the

shaded rectangles is an upper

Riemann sum.

390 Chapter 5 The Integral

maximum value on I

at u

525 and its minimum value at ‘

523. Continuing to

the other three subintervals, we ﬁnd that u

523, ‘

521, u

521, ‘

5 0, u

5 3,

and ‘

5 1. (Because f(x) is maximized on I

at both x 521andx 5 1, we could

equally well have set u

5 1.) Substituting these values into the formulas for the

upper and lower Riemann sums, we obtain

Rðf ; U

Þ 5

j5 1

f ðu

ÞΔx

5 f ð25Þ2 1 f ð23Þ2 1 f ð21Þ2 1 f ð3Þ2

5 2ð21 1 5 2 3 1 5Þ

5 56

and

Rðf ; L

Þ 5

j5 1

f ð‘

ÞΔx

5 f ð23Þ2 1 f ð21Þ2 1 f ð0Þ2 1 f ð1Þ2

5 2ð5 2 3 2 4 2 3Þ

5210:

INSIGHT

Notice that the Riemann sum R( f, S

) 5215/2 calculated in Example 1

lies between the upper and lower Riemann sums R( f, U

) 5 56 and R( f, L

) 5210,

which are calculated in Example 2. The following theorem generalizes this observation

and states another key fact about upper and lower Riemann sums.

THEOREM 1

Suppose that f is continuous on an interval [a, b].

a. If S

5 fs

, , s

g is any choice of points associated with the uniform

partition of order N, then

Rðf ; L

Þ# Rðf ; S

Þ# Rðf ; U

Þ: ð5:2:2Þ

b. The numbers R( f, L

) and R( f, U

) become arbitrarily close to each other

for N sufﬁciently large. That is,

lim

N-N



Rðf ; U

Þ2 Rðf ; L



5 0: ð5:2:3Þ

1

11 3

335

1

m Figure 6

5.2 The Riemann Integral 391

Proof. It follows from the deﬁnitions of ‘

and u

that

f ð‘

Þ# f ðs

Þ# f ðu

for every s

in I

. If we multiply each term by the positive quantity Δx and sum over

j 5 1, 2, . . . , N, then we obtain

j5 1

f ð‘

ÞΔx #

j5 1

f ðs

ÞΔx #

j5 1

f ðu

ÞΔx;

which is the assertion of Theorem 1a.

Theorem 1b appears to be plausible when we look at examples. Refer again to

Figures 4 and 5, which illustrate typical upper and lower Riemann sums. The area

the shaded rectangles in Figure 7 represents the difference R( f, U

) 2 R( f, L

)

for N 5 6. In Figure 8, we increase the number of subintervals to 30. Observe that

the difference between the upper and lower Riemann sums, again repres ented by

the area of the shaded rectangles, is signiﬁcantly smaller. Theorem 1b follows from

an important property of contin uous functions on closed, bounded intervals.

According to that property, which is proved in texts on advanced calculus, given a

positive ε, there is a positive δ such that f (s) is within ε of f (t), provided that s and t

are points in [a, b] within δ of each other. If we take N large enough so that Δx 5

(b 2 a)/N , δ, then u

and ‘

are within δ of each other for each j. Therefore

0 # Rðf ; U

Þ2 Rðf ; L

Þ 5

j5 1

ðf ðu

Þ2 f ð‘

ÞÞ  Δx ,

j5 1

ε  Δx

5 ε

j5 1

Δx 5 ε ðb 2 aÞ:

Because ε is arbitrary, we have shown that R( f, U

) 2 R( f, L

) can be made

arbitrarily small by taking N sufﬁciently large, which is Theorem 1b. ’

The Riemann Integral In Section 5.1, we deﬁned the area under the graph of a positive function to be the

limit as N tends to inﬁnity of right endpoint approximations. This deﬁnition will be

the basis of our limit deﬁnition for general Riemann sums.

DEFINITION

Suppose that f is a function deﬁned on the interval [a, b]. We say

that the Riemann sums R( f, S

) tend to the real number ‘ (or that ‘ is the limit

of the Riemann sums R( f, S

)) as N tends to inﬁnity, if, for any ε . 0, there is a

positive integer M such that

jRðf ; S

Þ2 ‘j, ε

for all N greater than or equal to M and any choice of S

. If this is the case, we

say that f is integrable on [a, b], and we denote the limit ‘ by the symbol

f ðxÞdx:

This numerical quantity is called the Riemann integral of f on the interval [a, b].

The operation of going from the function f to the number

f ðxÞdx is called

integration.

 bx

a  x

m Figure 7 The total area

enclosed by the shaded rectangles

is Rðf ; U

Þ2 Rðf ; L

Þ.

m Figure 8 The area of the

shaded region decreases as the

number N of subdivisions

increases.

392 Chapter 5 The Integral

Let us examine the components of the notation for the Riemann integral. The

elongated “S” symbol is called the integral sign and is used to remind us that the

integral is a limit of sums. The left and right endpoints of the interval [a, b]

are called the limits of integration. We refer to a as the lower limit of integration and

b as the upper limit of integration. The expression f (x) is called the integrand. For

now, the expression dx serves only to remind us of the variable of integration. We

may think of dx as the inﬁnitesimal limit of Δx as Δx tends to zero. In later work,

dx will be a useful device for helping us transform integrals into new integrals.

Only the presence of limits of integration serves to distinguish the Riemann

integral

f ðxÞdx from the indeﬁnite integral

f ðxÞdx from Section 4.9 (in Chapter

4). To emphasize the distinction, we sometimes refer to the Riemann integral

f ðxÞdx as a deﬁnite integral. As the nearly identical notations for

f ðxÞdx

and

f ðxÞdx suggest, there is an important relatio nship between the two

types of integrals. Later in this section, we learn that indeﬁnite integrals may be

used to calculate deﬁnite integrals. First, we state a theorem that assures the

existence of the deﬁnite integral

f ðxÞdx for most of the functions that we

encounter in calculus .

THEOREM 2

If f is continuous on the interval [a, b], then f is integrable on [ a , b].

That is, the Riemann integral

f ðxÞdx exists.

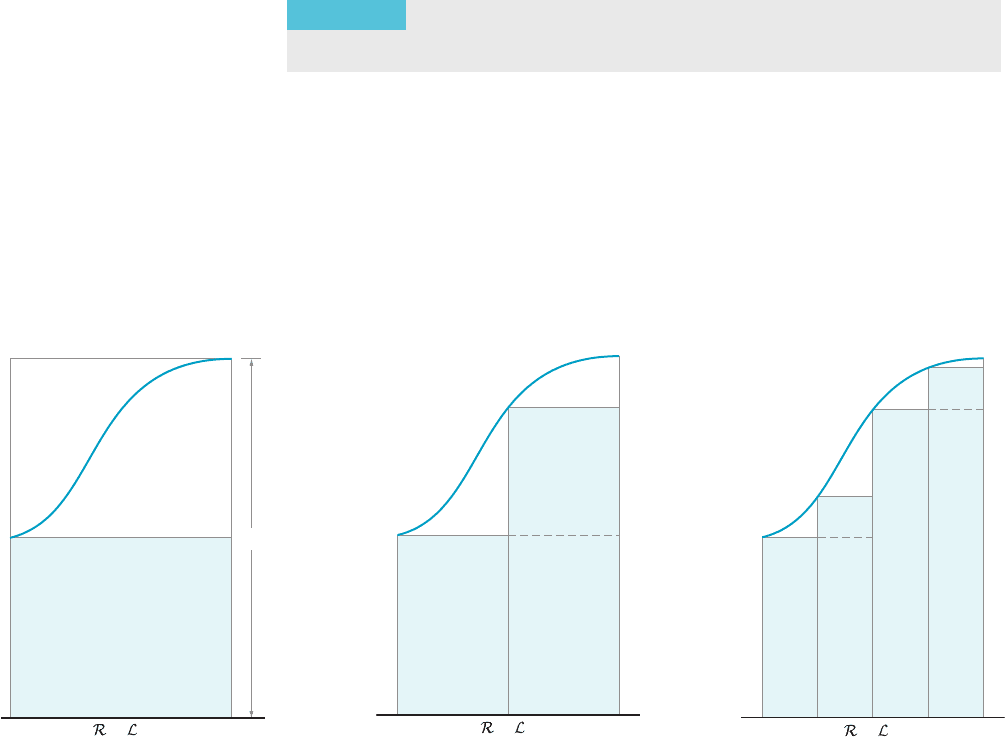
Proof. The

proof of this assertion involves technical details that are best left to a

text on advanced calculus. The following simple observations, however, give a good

idea of what is involved. Suppose f is increasing and positive on [a, b]. The areas of

the shaded regions in Figures 9a, 9b, and 9c represent R( f, L

) for N 5 1, 2, 4. The

amount by which R( f, L

) exceeds R( f, L

) is represented by the area of the

rectangle that lies above the dashed line in Figure 9b. Similarly, the amount by

which R( f, L

) exceeds R( f, L

) is represented by the area of the rectangles that lie

above the dashed lines in Figure 9c. If we continue to bisect each subinterval, we

obtain an increasing sequence of lower Riemann sums that is bounded above by

f(b)

( f,

)

m Figure 9a

( f,

)

m Figure 9b

( f,

)

m Figure 9c

5.2 The Riemann Integral 393

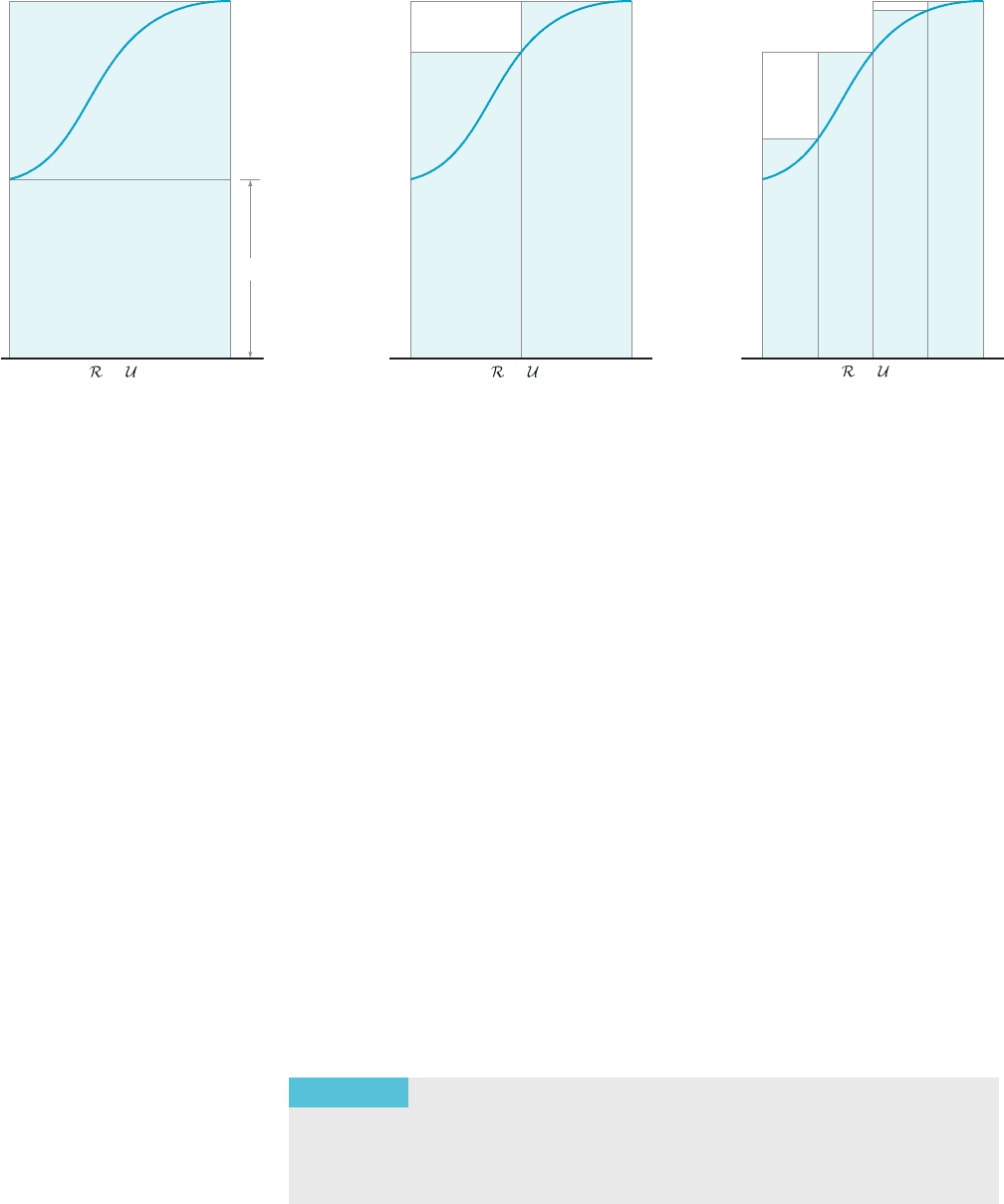
f (b) (b 2 a) (the area of the circumscribed rectangle shown in Figure 9a). We also

obtain a decreasing sequence of upper Riemann sums that is bounded below by

f (a) (b 2 a), as shown in Figure 10. According to the Monotone Convergence

Property of the real numbers (Section 2.6 in Chapter 2), both sequences of upper

and lower Riemann sums converge. We infer from limit (5.2.3) that the sequences

must converge to the same number. Call this common limit ‘. Let ε be an arbitrary

positive numbe r. Because the sequences fR( f, L

)g and fR( f, U

)g converge to ‘,

there is an integer M such that 0 # ‘ 2 R( f, L

) , ε/2 and 0 # R( f, U

) 2 ‘ , ε/2

for all N with M # N. Using inequality (5.2.2), we see that, for every N with M # N

and any choice of points S

,wehave

jRðf ; S

Þ2 ‘j # Rðf ; U

Þ2 Rðf ; L

5 Rðf ; U

Þ2 ‘ 1 ‘ 2 Rðf ; L

5 ε=2 1 ε=2

5 ε;

which shows that f has a Riemann integral on the interval [a, b]. ’

Calculating Riemann

Integrals

Calculating deﬁnite integrals by the method of Riemann sums is tedious and usually

difﬁcult. Fortunately, our next theorem shows how indeﬁnite integrals, or anti-

derivatives, can be used to evaluate deﬁnite integrals without considering Riemann

sums. Recall from Section 4.9 in Chapter 4 that F is an antiderivative of f on an open

interval (a, b)ifF

(x) 5 f (x) for all x in (a, b). If we say that F is an antiderivative of f

on the closed interval [a, b], then we mean that F is continuous on [a, b]andF

5 f on

(a, b). As you read the proof of Theorem 3, notice how crucial it is to have ﬂexibility

in the choice of points fs

g that we use to form the Riemann sums.

THEOREM 3

Suppose that F is an antiderivative of a continuous function f on

[a, b]. Then,

f ðxÞdx 5 FðbÞ2 FðaÞ: ð5:2:4Þ

( f,

)

f(a)

m Figure 10a

( f,

)

m Figure 10b

( f,

)

m Figure 10c

394 Chapter

5 The Integral