Бороденко В.А. Исследование систем управления в среде MATLAB
Подождите немного. Документ загружается.


61
- от коэффициента передачи по каналу ошибки от задания или
возмущения – пропорционально;
- от общего коэффициента усиления системы k
c
= k
p
∙k
0
– обратно
пропорционально.
Относительная величина установившейся ошибки называется
коэффициентом статизма (статизмом) системы по соответствующему
каналу.
c
r
r
k1
1
r
S
)(
– статизм от задания,
c
0
f
f
k1
k
f
S
)(
– статизм от возмущения.
Ошибку регулирования и статизм можно уменьшить, увеличи-
вая общий коэффициент усиления системы.
По заданной величине статизма (относительной статической
ошибки) системы можно выбрать требуемый коэффициент усиления.
Пример: пусть допустимая ошибка не должна превышать зна-
чения ε(∞) = 2% или ε(∞) = 0,02, тогда коэффициент усиления не мо-
жет быть менее
49
020
0201
k
k1
1
020
c
c
,
,
, .
Изменим при тех же условиях порядок астатизма ν = 1, для чего
введем в состав регулятора (рисунок 1.35, а) звено с нулевым корнем в
знаменателе (интегратор), и рассчитаем значение установившейся
ошибки по заданию и от возмущения, как конечное значение оригина-
ла.
а б
Рисунок 1.35
c
c
ks
s
s
k
1
1
sW
r
)(
;
0
s
1
s
ks
s
0sc
r
)(
.
c
0
c
0
ks
sk
s
k
1
k
sW
f
)(
;
0
s
1
s
ks
sk
0s
c
0
f
)(
.
r(t)
ε(t)
u(t)
f(t)
y(t)
s
k
p
k
0
r(t)
ε(t)
u(t)
f(t)
y(t)
k
p
s
k
0

62
Увеличение астатизма разомкнутой системы при том же воздей-
ствии привело к исключению статической ошибки.
Введем теперь интегратор в ПФ объекта (рисунок 1.35, б).
c
ks
s
sW
r
)(
; осталось
0
ks
s
s
0s
c
r
)(
.
c
0
ks
k
sW
f
)(
, изменилось 0
k
k
c
0
f
)(
.
Следовательно, статическую ошибку устраняют только интегра-
торы, размещенные вне цепи прямой связи сигнала ошибки.
Если, выделив нулевые корни, записать ПФ системы в виде
W(s) = W
0
(s)/s
ν
, а входное воздействие в виде R(s) = M(s)/s
r
, то при
r < ν+1 получим ε
r
(∞)=0; при r = ν+1 получим ε
r
(∞)=const; и, нако-
нец, при r > ν+1 получим ε
r
(∞)= f(t).
1.5.7 Коэффициенты ошибок
Установившийся динамический режим имеет место при возму-
щенном движении системы с момента затухания свободной состав-
ляющей переходного процесса. Считая, что входное воздействие ап-
проксимируется полиномом от t, т. е.разлагается в степенной ряд
)(
!
...)( t1
m
t
A
2
t
AtAAtr
m
m
2
210
,
для расчета вынужденной составляющей ошибки используют метод
коэффициентов ошибок.
По этому методу передаточную функцию ошибки представляют
в виде аналогичного ряда
2
0 1 2
( ) ...
n
n
W s C C s C s C s
, где С
0
– ко-
эффициент статической ошибки (позиционной), С
1
– коэффициент
ошибки по скорости, С
2
– коэффициент ошибки по ускорению.
Сравнивая две формы записи передаточной функции ошибки,
находим значения коэффициентов ошибок (в обоих случаях полиномы
начинаются со свободного члена)
m
m
2
210
n
01nn
m
01mm
sCsCSCC
sasaa
sbsbb
sW
...
...
...
)(
s
0
→ b
m
=a
n
C
0
→
m
n
0
b
a
1
C ,
Нормирование
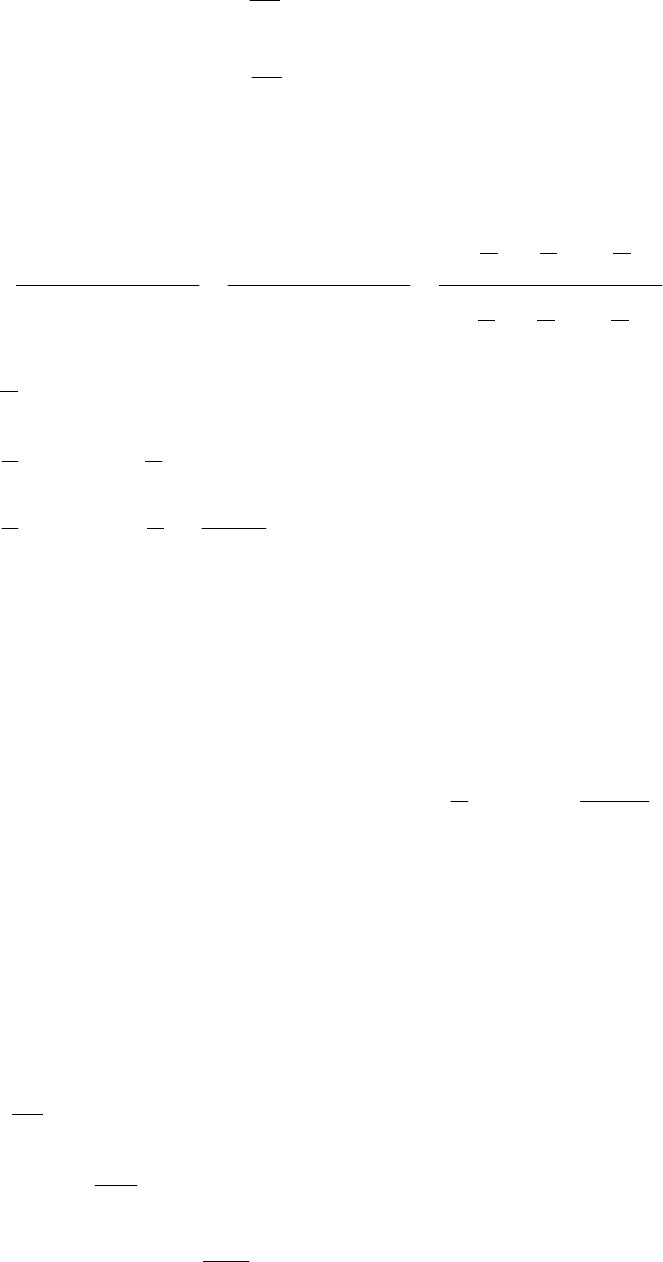
63
s
1
→ →
01n1m
n
1
Cab
a
1
C
,
s
2
→ →
11n02n2m
n
2
CaCab
a
1
C
и т.д.
Пример: найдем три первых коэффициента ошибок для системы
(записываем ПФ ошибки наоборот и нормируем по свободному чле-
ну)
32
32
32
32
23
23
231
1
231
0
23
230
32
32
)(
s
k
s
k
s
k
s
k
s
k
s
k
sssk
sss
ksss
sss
sW
r
.
00
k
1
C
0
,
k
1
011
k
1
C
1
)(
,
2
2
k
1k3
k
1
1033
k
1
C
)(
.
Вынужденная составляющая ошибки равна
)()()()( trCtrCtrCt
210r
.
Пусть задающее воздействие равно 2atvtrr
2
0
/ , тогда для
данной системы производные
at
v
r
,
a
r
и установившаяся ди-
намическая ошибка при С
0
= 0 имеет вид a
k
1k3
atv
k
1
t
2
r
)()(
.
Обычно вычисляют три первых коэффициента ошибок. Общий
коэффициент усиления разомкнутой цепи k (добротность) находится в
знаменателе всех выражений, обуславливает уменьшение всех видов
ошибок и является главным фактором повышения точности замкнутой
системы автоматического регулирования.
Коэффициенты передачи составляющих воздействия определя-
ются по ПФ разомкнутой системы и называются:
n
m
ст
a
b
K – позиционная добротность;
1
0,
m
n
n
b
a K
a
– добротность по скорости;
1
2
0, 0,
m
n n
n
b
a a K
a
– добротность по ускорению.

64
Так, для указанной системы W
раз
(s) = k/(2s
3
+ 3s
2
+ s), откуда
добротность по скорости K
Ω
= k/1 = k.
1.6 Синтез систем автоматического регулирования
1.6.1 Типовые динамические звенья
Для составления структурной схемы реальные элементы заме-
няются типовыми звеньями, характеризующими динамику процесса
(линейные звенья) или его статику (нелинейные звенья).
ПФ типовых звеньев нормируют по свободному члену, тогда
общий коэффициент k = b
m
/a
n
сразу равен коэффициенту усиления в
установившемся режиме.
К типовым динамическим звеньям обычно относят: усилитель-
ное 1, интегрирующее 2, инерционное 3, звено второго порядка 4
(апериодическое, колебательное, консервативное), дифференцирую-
щее 5, форсирующее звено первого и второго порядка 6, звено чистого
запаздывания 7. В передаточной функции системы они занимают сле-
дующее место
Типовые звенья являются не только устойчивыми, но и мини-
мально-фазовыми, т. е. при одинаковых с другими звеньями АЧХ
имеют наименьшие по модулю фазовые характеристики (минималь-
ную конфигурацию годографа). В знаменателе и в числителе ПФ у
них отсутствуют корни с положительной действительной частью.
Между амплитудной и фазовой характеристиками таких звеньев име-
ется однозначное соответствие, поэтому достаточно иметь АЧХ, а
ФЧХ строится по шаблону.
Усилительное звено (пропорциональное, безинерционное) – это
звено, выходная величина которого в любой момент времени про-
порциональна входной величине. Возможно как усиление (k > 1), так
и ослабление (k < 1) сигнала. Передаточная функция W(s)=k. Примеры
реализации – делитель на резисторах, рычажная передача, сопряжен-
ная пара шестерен, инвертирующий усилитель.
Интегрирующее звено (астатическое, нейтральное) – это звено,
скорость изменения выходной величины которого пропорциональна
входной величине. Иначе – выходная величина пропорциональна ин-
1 5 2 3 6 4 6 7
s
e
sTsTsTs
ssss
ksW
)1)(1(
)1)(1(
)(
2
2
10
2
2
10
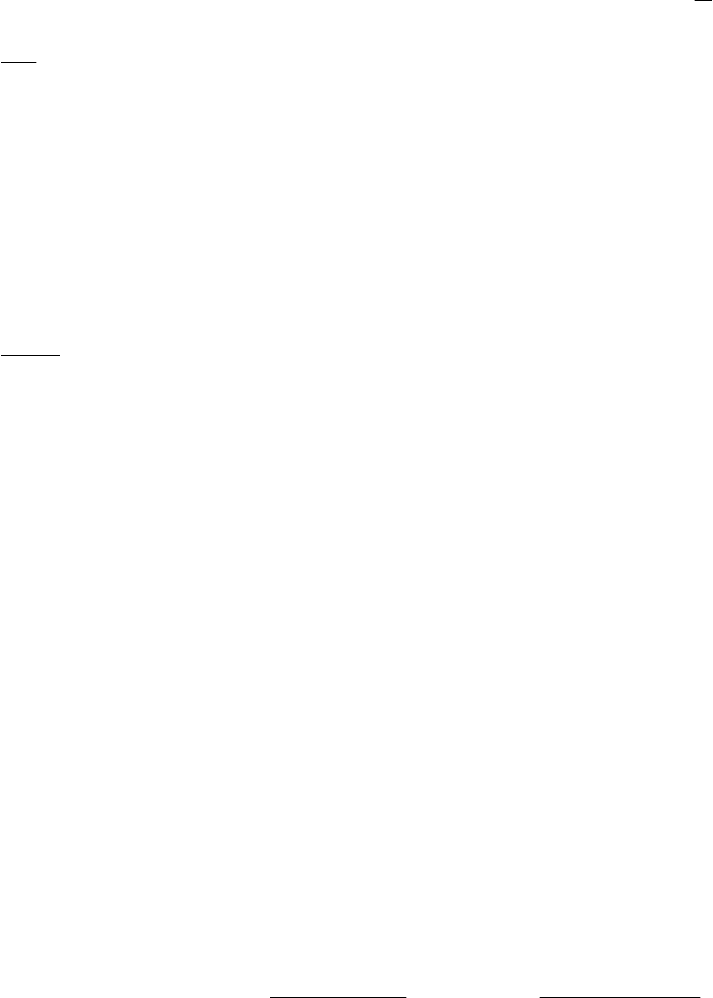
65
тегралу входной величины. Передаточная функция
s
k
W(s) или
sT
1
W(s)
и
.
На всех частотах интегратор создает отставание выходного сиг-
нала от входного на 90
о
, он является фильтром низких частот (ФНЧ).
Примеры реализации – емкость, наполняемая насосом с постоянной
производительностью, интегратор на операционных усилителях.
Инерционное звено (апериодическое звено первого порядка) –
это звено, выходная величина которого при скачке на входе стремится
к установившемуся значению по экспоненте. Передаточная функция
1Ts
k
W(s)
. Является типичным фильтром низких частот (ФНЧ). При
увеличении времени исследования t>>T инерционное звено приобре-
тает свойства усилительного звена, а при уменьшении t<<T – интег-
рирующего. Примеры реализации – нагревательная печь, лампа нака-
ливания, термопара, электродвигатель, RC-делитель.
Постоянная времени T численно равна длине отрезка, отсекае-
мого на линии установившегося значения касательной, восстановлен-
ной к характеристике из начала координат. Иначе – это время дости-
жения 0,63 от установившегося значения. Время установления (за-
вершения переходного процесса) инерционного звена равно примерно
3Т (с погрешностью 5 %).
Звено второго порядка – это название нескольких звеньев, у ко-
торых вид дифференциального уравнения одинаков, конкретный тип
звена определяется характером корней квадратного трехчлена.
Апериодическое звено – это звено второго порядка, реакция ко-
торого при скачке на входе образуется двумя противопоставленными
экспонентами. Оно имеет место при выполнении условия a
1
2
≥ 4a
0
, т.
е. при чисто вещественных корнях характеристического уравнения
D(s)=a
0
s
2
+a
1
s+1=0, нормированного по свободному члену. Переда-
точная функция звена
1sTsT
k
W(s)
1
22
2
или
1sT1sT
k
W(s)
43
.
Постоянная Т
4
– меньшая из двух постоянных времени Т
4
<<T
3
.
Между постоянными времени выполняются соотношения T
1
=T
3
+T
4
,
T
2
2
=T
3
T
4
. Критический случай имеет место при кратных корнях T
3
=T
4
.
Реализация соответствует двум последовательно соединенным
инерционным звеньям. Характерная особенность АФЧХ – модуль
вектора постоянно убывает при увеличении частоты от 0 до бесконеч-
ности. Характерная особенность ЛАЧХ – два перелома вниз на часто-
тах сопряжения с отклонением каждый раз на -20 дБ/дек.

66
Колебательное звено – это звено, выходная величина которого
при скачке на входе стремится к новому установившемуся значению,
совершая относительно него экспоненциально затухающие колебания.
Звено имеет место при условии 0<a
1
2
<4a
0
, соответствующем ком-
плексным сопряженным корням характеристического уравнения.
ПФ звена
1s2TsT
k
W(s)
22
или
2
0
2
2
0
s
k
W(s)
.
Здесь – показатель затухания (демпфирования), для колеба-
тельного звена лежит в пределах 0 << 1, для апериодического звена
второго порядка 1, = /T =
0
= 1/(2T
0
)∙ln(a
2
/a
1
).– действитель-
ная часть корня характеристического уравнения,
0
– собственная
частота колебаний. Выброс (пик) ЛАЧХ h наблюдается на частоте со-
пряжения
с
=
2
0
2
при ξ < 0,707. ЛАЧХ имеет один перелом с ук-
лоном –40 дБ/дек. Без резонанса разница между реальной и асимпто-
тической ЛАЧХ равна минус 6 дБ, большее значение уже говорит о
наличии резонанса. Чем меньше , тем выпуклей АФЧХ, тем выше
пик ЛАЧХ, тем круче ЛФЧХ в точке резонанса.
Примеры реализации – физический маятник, защемленная бал-
ка, вибрирующий контакт, качания синхронного электродвигателя в
процессе синхронизации с источником питания и т. п.
Консервативное звено (идеальное колебательное) – это звено,
выходная величина которого при скачке на входе совершает колеба-
ния с постоянной амплитудой. Оно имеет место при условии a
1
= 0
( = 0), т.е. при чисто мнимых корнях характеристического уравнения.
Передаточная функция
1sT
k
W(s)
22
или
2
0
2
2
0
s
k
W(s)
.
Примеры реализации – генератор синусоидальных колебаний.
Идеальное дифференцирующее звено – это звено, выходная ве-
личина которого пропорциональна скорости изменения входной вели-
чины. Передаточная функция ksW(s)
или
sTW(s)
д
.
Идеальное дифференцирующее звено создает опережение вы-
ходного сигнала относительно входного на 90
о
для всех частот и явля-
ется фильтром высокой частоты (ФВЧ). Физически такое звено не-
осуществимо (m > n), поэтому на практике используется реальное
дифференцирующее звено.
Реальное дифференцирующее звено – это совокупность инерци-
онного и идеального дифференцирующего звеньев, соединенных по-
следовательно. Передаточная функция
1Ts
ks
W(s)
.

67
Реальное интегрирующее звено соответствует последователь-
ному включению интегратора с инерционным звеном. Передаточная
функция
1)s(Ts
k
W(s)
.
Форсирующее звено первого порядка – самостоятельного значе-
ния не имеет, как и форсирующее звено второго порядка, может ис-
пользоваться только в совокупности с другим звеном при m ≤ n. У
форсирующих звеньев перелом ЛЧХ происходит вверх, а выброс кор-
ректируется вниз. Передаточная функция
1TskW(s) .
Реализация соответствует параллельному соединению пропор-
ционального и дифференцирующего звеньев.
Запаздывающее звено (звено чистого запаздывания) – повторяет
входное воздействие на выходе без изменения масштаба или формы,
но с задержкой на время чистого запаздывания. Передаточная функ-
ция
-s
eW(s)
Наиболее характерный пример реализации – транспортер. За-
паздывание в системе имеет место всегда, если точки воздействия на
объект регулирования и контроля результатов воздействия разнесены
в пространстве, например, при регулировании толщины проката.
Для приведения передаточной функции звена транспортного за-
паздывания к обычному виду рациональной дроби используют разло-
жение в ряд Паде, например, разложение первого порядка
s501
s501
e
s
,
,
.
1.6.2 Непрерывные регуляторы и законы регулирования
Законом регулирования называют функциональную связь между
управляющим воздействием на выходе регулятора и ошибкой регули-
рования на его входе. Назначение регулятора – свести к минимуму
(нулю) свою входную величину. Перечислим типы линейных непре-
рывных регуляторов и законы регулирования:
- П-регулятор – регулирование по отклонению действительного
значения управляемого параметра от заданного;
- И-регулятор – регулирование по интегралу отклонения по вре-
мени;
- ПД-регулятор – регулирование по отклонению и производным
отклонения по времени;
- ПИ-регулятор (изодром) – регулирование по отклонению и ин-
тегралу отклонения по времени;
68
- ПИД-регулятор - регулирование по отклонению, интегралу и
производным отклонения по времени.
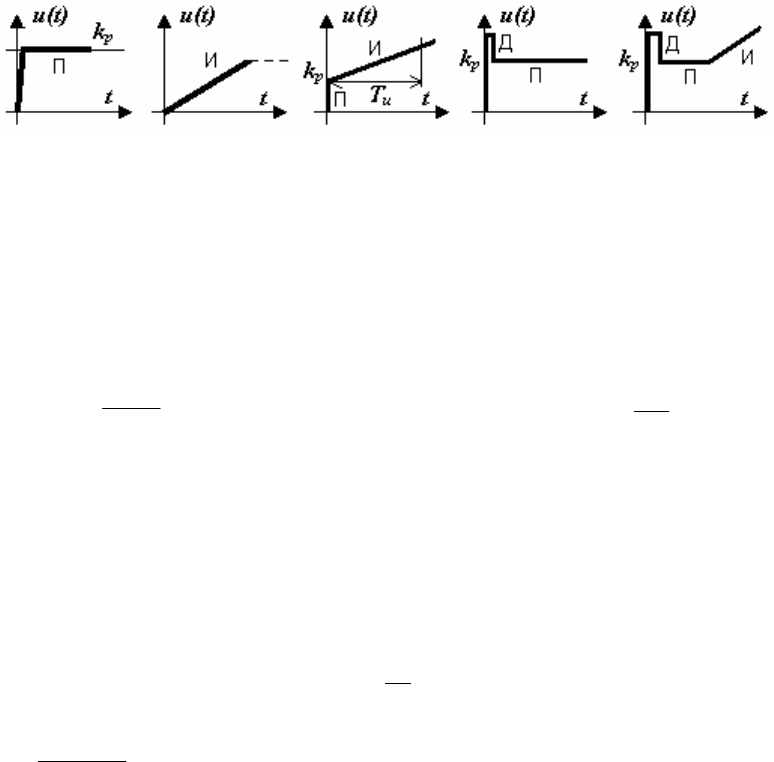
Пропорциональный П-регулятор (статический) имеет закон ре-
гулирования u(t) = k
р
(t), передаточную функцию W(s) = k
р
и характе-
ристику регулирования (рисунок 1.36, а). Он обеспечивает самый бы-
стрый переходный процесс, но имеет статическую ошибку регулиро-
вания.
а б в г д
Рисунок 1.36
Величину 1/k
р
, называют статизмом или коэффициентом нерав-
номерности регулятора. Разность между максимальным и минималь-
ным установившимися значениями регулируемой величины называет-
ся абсолютной статической неравномерностью.
Интегральный И-регулятор (астатический) имеет закон регули-
рования
)(
)(
t
dt
tdu
T
и
, передаточную функцию
sT
sW
и
1
)( и характе-
ристику регулирования (рисунок 1.36, б). Достоинство регулятора –
отсутствие статической ошибки, в установившемся режиме заданное
значение регулируемой величины поддерживается при любом значе-
нии возмущения. Недостаток – большое время нарастания (регулиро-
вания).
Пропорционально-интегральный ПИ-регулятор (изодром) имеет
закон регулирования dtt
T
tktu
и
p
0
)(
1
)()(
, передаточную функцию
sT
sTk
sW
и
иp
1
)(
и характеристику регулирования (рисунок 1.36, в). За
счет П-составляющей ускоряется процесс перехода к новому устано-
вившемуся состоянию, за счет И-составляющей исключается остаточ-
ная неравномерность. Регулятор реализуется параллельным соедине-
нием интегратора и усилительного звена. Постоянная времени T
и
на-
зывается также временем удвоения, поскольку численно равна време-
ни удвоения значения пропорциональной части.
Пропорционально-дифференциальный ПД-регулятор (или регу-
лятор с предварением) имеет ПФ
sTksW
дp
)(
, закон регулирова-

69
ния
dt
td
Ttktu
дp
)(
)()(
, и характеристику регулирования (рисунок
1.36, г). После броска управления в момент появления возмущения ха-
рактеристика переходит на уровень, соответствующий позиционной
части с коэффициентом регулирования k
p
. Включение производной в
закон регулирования позволяет предвидеть изменение регулируемого
параметра, что особенно важно при резких и больших возмущениях
для объектов со значительной инерцией. Вследствие предварения
время переходного процесса и амплитуда колебаний регулируемой
величины могут быть уменьшены (это другой способ исключения
ошибки регулирования, более быстрый по сравнению с действием ин-
тегратора, но менее точный).
Регулятор реализуется параллельным соединением дифферен-
цирующего и усилительного звеньев (в виде форсирующих звеньев
первого и второго порядка). В энергетике называется регулятором
сильного действия и применяется для форсировки напряжения генера-
торов при коротком замыкании (КЗ) в энергосистеме.
Пропорционально-интегрально-дифференциальный или ПИД-
регулятор (изодром с предварением) имеет закон регулирования
dt
td
Tdtt
T
tktu
д
и
p
)(
)(
1
)()(
0
, ПФ
sT
sTksTT
sW
и
иpид
1
)(
2
и ха-
рактеристику регулирования (рисунок 1.36, д). В момент возмущения
превалирует регулирование по производной отклонения выходной ве-
личины от заданного значения, интегрирующая часть действует на
устранение ошибки в течение всего времени ее существования, но
проявляется в конце переходного процесса.
Для всех регуляторов с И-составляющей характерно то, что при
приближении ошибки (т. е. входного сигнала регулятора) к нулю вы-
ходная величина регулятора (управление) фиксируется на некотором
уровне, который может не совпадать с предшествующим уровнем
управляющего воздействия. Д-регулятор отдельно не применяют, так
как его действие приводит к неустойчивости системы, которая начи-
нает реагировать на любые помехи и колебания входной величины, не
осуществляя в то же время регулирование в установившемся режиме.
1.6.3 Системы регулирования с запаздыванием
Системы с запаздыванием имеют, по крайней мере, одно звено,
реакция на выходе которого отстает по времени от входного воздей-
ствия на постоянную величину τ. Такой объект описывается диффе-
ренциально-разностным уравнением с запаздывающим аргументом
70
kxtyayapyaypa
321
2
0
)(
.
Здесь член )(
tya
3
соответствует изображению
s
3
esYa
)( .
Если входное воздействие txexx
m
tj
m
sin , то реакция системы
имеет вид )](sin[
)(
tyeyy
m
tj
m
. Характерными примерами
систем с запаздыванием являются системы дозирования вещества, пе-
ремещаемого по транспортеру, измерения толщины проката на рас-
стоянии от регулируемых валков, управления объектами на большом
расстоянии по радио. Рассмотрим особенности их проектирования.
Звено чистого запаздывания может находиться в цепи прямой
связи
s
p
s
0
e
sD
sN
kesWsW
)(
)(
)()( , тогда после замыкания ПФ сис-
темы будет иметь вид Ф(s)
s
s
p
e
eskNsD
skN
sW1
sW
)()(
)(
)(
)(
. Если
звено запаздывания в прямой цепи охвачено местной обратной свя-
зью, либо находится в цепи главной обратной связи, выражение ус-
ложняется, и эти случаи необходимо рассматривать отдельно.
Из комплексного коэффициента передачи разомкнутой системы
j
0
ejWjW
)()( следует )()(
0
AA
и
)()(
0
, т. е.
наличие элемента запаздывания не изменяет амплитуду частотной ха-
рактеристики, но существенно влияет на ее фазу, причем с ростом
частоты фазовый сдвиг все более смещается к минус бесконечности.
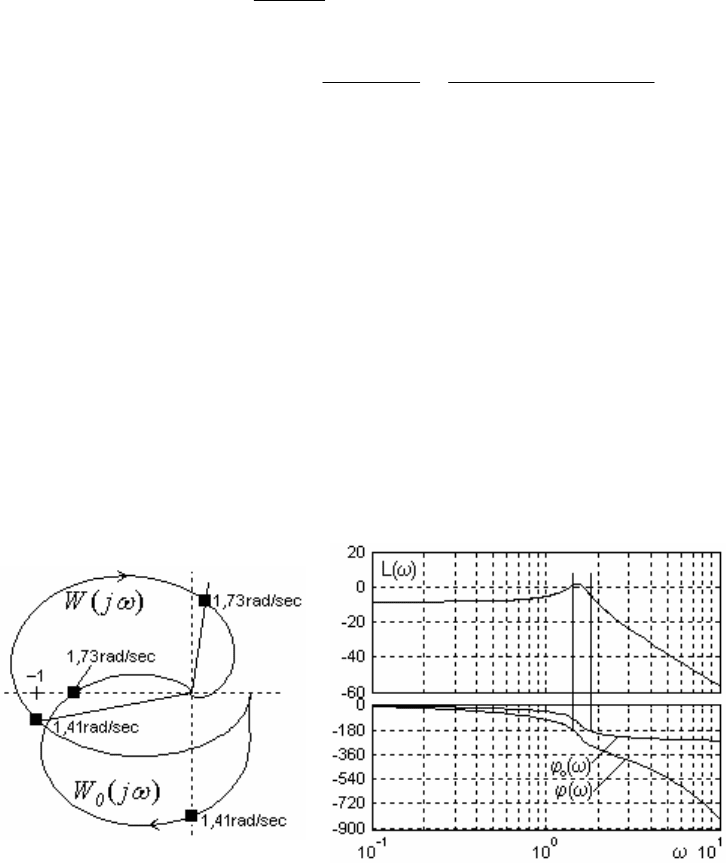
Поэтому векторы А(ω) для всех частот поворачиваются по часовой
стрелке на угол τω и годограф W(jω) принимает спиралевидную фор-
му, асимптотически приближаясь к началу координат (рисунок 1.37,
а).
а б
Рисунок 1.37
