Бороденко В.А. Исследование систем управления в среде MATLAB
Подождите немного. Документ загружается.

91
обеспечив показатели качества переходного процесса ошибки наблю-
дателя t
рег
= 1 с, σ = 30 %.
По матрицам коэффициентов объекта регулирования определя-
ем его передаточную функцию (объект неустойчив)
1 3 1
; = ; 2 1
1 1 1
A B C
1
2
3 8
( ) ( )
2 4
o
s
W s s
s s
C 1 A B
.
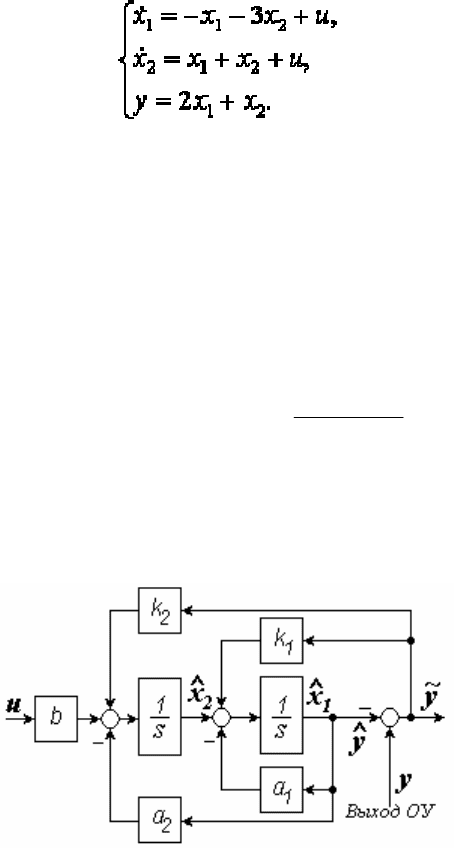
В фильтре Калмана второго порядка с дифференциальным урав-
нением р
2
y + a
1
py + a
2
y = bu компенсирующая добавка образуется об-
ратными связями с коэффициентами k
1
, k
2
(рисунок 1.45).
Рисунок 1.45
В соответствии с матрицей
1 1
2 2
( ) 1
( ) 0
a k
a k
A
характеристиче-
ский полином наблюдателя имеет вид D(s) = s
2
+(a
1
+k
1
)s + (a
2
+ k
2
)
или D(s) = s
2
+(–2 +k
1
)s + (4 + k
2
).
Исходя из требований к качеству переходного процесса наблю-
дателя модуль действительной части α
min
корней его характеристиче-
ского уравнения при Δ = 5 % должен быть не менее, чем 3/t
рег
= 3, то-
гда мнимая часть равна β = –πα
min
/ln(σ) = –3,1415926*3/ln(0,3) = 7,83.
По двум выбранным корням –3 ± j7,83 определяем вид желаемого ус-
тойчивого характеристического полинома 27.706)(
2
sssD
ж
.
Из равенства D(s) = D
ж
(s) находим неизвестные коэффициенты
корректирующих обратных связей k
1
= 6 + 2 = 8, k
2
= 70,27 – 4 = 66,27.
92
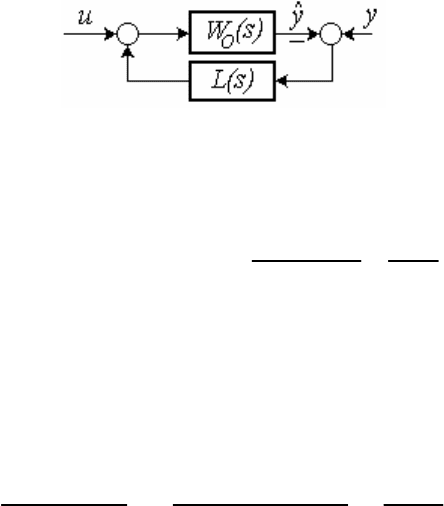
Пример: рассчитать параметры наблюдателя в виде фильтра
Калмана (рисунок 1.46) с компенсирующим звеном, имеющим переда-
точную функцию L(s) = k(τ
1
s + 1)/(τ
2
s + 1), при тех же требованиях к
качеству переходного процесса наблюдателя и параметрах ПФ модели
объекта регулирования W
o
(s).
Рисунок 1.46
Передаточная функция модели объекта регулирования равна
1
2
3 8 ( )
( ) ( )
2 4 ( )
o
s B s
W s s
s s A s
C 1 A B
,
а характеристическое уравнение наблюдателя имеет вид
( ) ( ) ( ) ( ) 0
D s A s B s L s
,
откуда, приравняв числитель нулю и нормируя, получаем
3 2
2 1 2 1
2 2 2
1 2 3 4 2 3 8 4 8
0
k k k k
s s s
.
Желаемый характеристический полином третьего порядка фор-
мируем из корней с одинаковой действительной частью –3 ± j7,83 и
–3, он равен D
ж
(s) = s
3
+ 9s
2
+ 88s + 211. Приравнивая D(s) = D
ж
(s), на-
ходим неизвестные коэффициенты k, τ
1
и τ
2
.
1.7.7 Проектирование модального регулятора
Модальным называется регулятор, параметры которого выбра-
ны по желаемому характеристическому многочлену замкнутой систе-
мы управления. Полагаем, что все переменные состояния объекта
управления доступны для измерения, и рассмотрим случай, когда ис-
пользуется П-регулятор. Модель объекта управления
1 2
2 2 1 1 2
1
x x
x a x a x bu
y x
Закон управления для объекта второго порядка имеет вид

93
u = Kr – k
1
x
2
–k
2
x
1
где K – коэффициент усиления П-регулятора, r – задание, k
1
, k
2
– ко-
эффициенты обратных связей регулятора по переменным состояния.
Подставив значение u в уравнение состояния, получим систему
уравнений, которая описывает замкнутую систему управления
1 2
2 2 2 1 1 1 2
1
( ) ( )
x x
x a bk x a bk x bKr
y x
,
и характеристический полином замкнутой системы
D(s) = s
2
+ (a
1
+ bk
1
)s + (a
2
+ bk
2
).
Неизвестные коэффициенты k
1
и k
2
обратных связей по пере-
менным состояния объекта можно определить из равенства полиному
желаемого вида D
ж
(s). Последний либо выбирают на основе заданных
значений перерегулирования % и времени регулирования t
п
. из ти-
повых (приложение Г), либо рассчитывают самостоятельно. Напри-
мер, параметры качества регулирования σ = 4,5 %, t
р
= 2,9 с при отсут-
ствии нулей обеспечит нормированный полином Баттерворта второго
порядка D
ж
(s) = s
2
+ d
1
s + d
2
= s
2
+ 1,14s + 1.
Приравняв коэффициенты полиномов при одинаковых степенях
s, получим k
1
= (d
1
– a
1
)/b, k
2
= (d
2
– a
2
)/b. Расчет существенно упро-
щается, если объект представлен в канонической форме управляемо-
сти с b = 1.
Коэффициент усиления K обычно находят из условия нулевой
статической ошибки: либо по коэффициентам передаточной функции
bK/(a
2
+ k
2
) = 1, откуда K = (a
2
+ k
2
)/b = d
n
/b
m
, либо из инверсии мат-
ричной передаточной функции K = (c(-A)
-1
b)
-1
при s = 0.
Если для измерения доступна только одна величина на выходе
y(t), для создания обратных связей по переменным состояния устанав-
ливают наблюдатель, либо в цепи главной обратной связи системы
используют ПД-регулятор (форсирующее звено) с эквивалентной пе-
редаточной функцией H
eq
(s).
Рассчитаем параметры модального регулятора для объекта
2 2
1 2
5
( )
3 1
o
o
k
W s
s a s a s s
при требованиях к качеству регулирования t
п
3 с; = 0 % , е(∞) =0.
Регулятор состоит из двух частей: обеспечивающей статические ха-

94
рактеристики системы W
s
(s) и обеспечивающей динамические харак-
теристики W
d
(s) (рисунок 1.47), для измерения доступна только вы-
ходная переменная y объекта.
Рисунок 1.47
Выберем интегратор (И-регулятор) в качестве W
s
(s) = k/s, чтобы
обеспечить нулевую статическую ошибку е(∞) = 0; пусть составляю-
щая регулятора, обеспечивающая заданные динамические свойства
равна W
d
(s) = (d
1
s +d
2
)/k
o
; здесь k, d
1
, d
2
– неизвестные коэффициенты,
k
o
– коэффициент передачи объекта регулирования.
Тогда характеристическое уравнение замкнутой системы равно
2
1 2
( ) ( 3 1 ) 5 0
D s s s s d s d k
или
3 2
1 2
( ) ( 3) ( 1) 5 0
D s s d s d s k
Выберем распределение корней, обеспечивающее заданное ка-
чество процессов, например, λ
1
= -2; λ
2
= -2,5; λ
3
= -3 (все действи-
тельные полюса обеспечат нулевое перерегулирование и время регу-
лирования близко к 3/2 = 1,5 с). Сформируем желаемое характеристи-
ческое уравнение третьего порядка
D(s) = (s - λ
1
)(s - λ
2
)(s - λ
3
) = s
3
+ 7,5s
2
+ 18,5s + 15 = 0.
Приравнивая коэффициенты при соответствующих степенях s,
получим расчетные соотношения d
1
+ 3 = 7,5; d
2
– 1 = 18,5; 5k = 15.
Отсюда находим параметры регулятора d
1
= 4,5; d
2
= 19,5; k = 3.
Пример: ПФ объекта регулирования после нормирования имеет
вид
3 2
100
( )
20,5 110 50
W s
s s s
,
заданные показатели качества: время регулирования 6 с, перерегули-
рование 0,02, выбрать параметры модального регулятора. Поскольку
объект представлен передаточной функцией и не все переменные со-
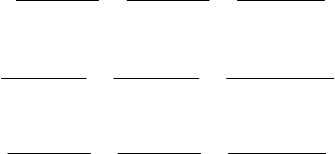
95
стояния измеряются, формируем наблюдатель состояния с параметра-
ми b = 100, a
10
= 20,5, a
20
= 110, a
30
= 50.
Исходя из требований к процессу регулирования замкнутой сис-
темы, выбираем корни s
1
, s
2
... s
n
и определяем эталонный (желаемый)
характеристический полином с коэффициентами a
1
... a
n
. Характери-
стический полином третьей степени содержит один действительный
корень и два комплексных сопряженных, по последним, полагая их
доминирующими, и будем формировать показатели качества регули-
рования.
При заданном времени регулирования t
рег
= 6 с степень устойчи-
вости для ошибки Δ = 5 % равна α
min
= 3/6 = 0,5, отсюда действитель-
ная часть комплексного корня будет равна -0,5. Действительный ко-
рень принимаем в 10 раз большим, т. е. -5, чтобы исключить его влия-
ние на переходный процесс. По заданной величине перерегулирова-
ния σ = 0,02 вычисляем степень колебательности μ = -π/ln(σ) =
= -3,1415926/ln(0,02) = 0,803, после чего можно вычислить мнимую
часть комплексного корня β = μ∙α
min
= 0,803∙0,5 = 0,401.
По значениям корней -5 и -0,5 ± j0,401 находим вид желаемого
характеристического полинома
05,241,56]401,0)5,0)[(5()(
2322
ssssssD
.
Из условия нулевой ошибки регулирования значение коэффици-
ента усиления регулятора K = a
n
/b = 2,05/100 = 0,0205. Значения ко-
эффициентов обратной связи по переменным состояния равны
,0732,7
05,2
5,206
3
101101
1,
a
aa
Kb
aa
k
oc
,0195,51
05,2
11041,5
3
202202
2,
a
aa
Kb
aa
k
oc
.3902,23
05,2
5005,2
3
303303
3,
a
aa
Kb
aa
k
oc
Замкнутая система регулирования (рисунок 1.48) содержит объ-
ект управления на выходе U(t), наблюдатель в форме, соответствую-
щей каноническому управляемому представлению, П-регулятор с ко-
эффициентом усиления К и обратными связями k
oc
по переменным со-
стояния, формируемым наблюдателем.
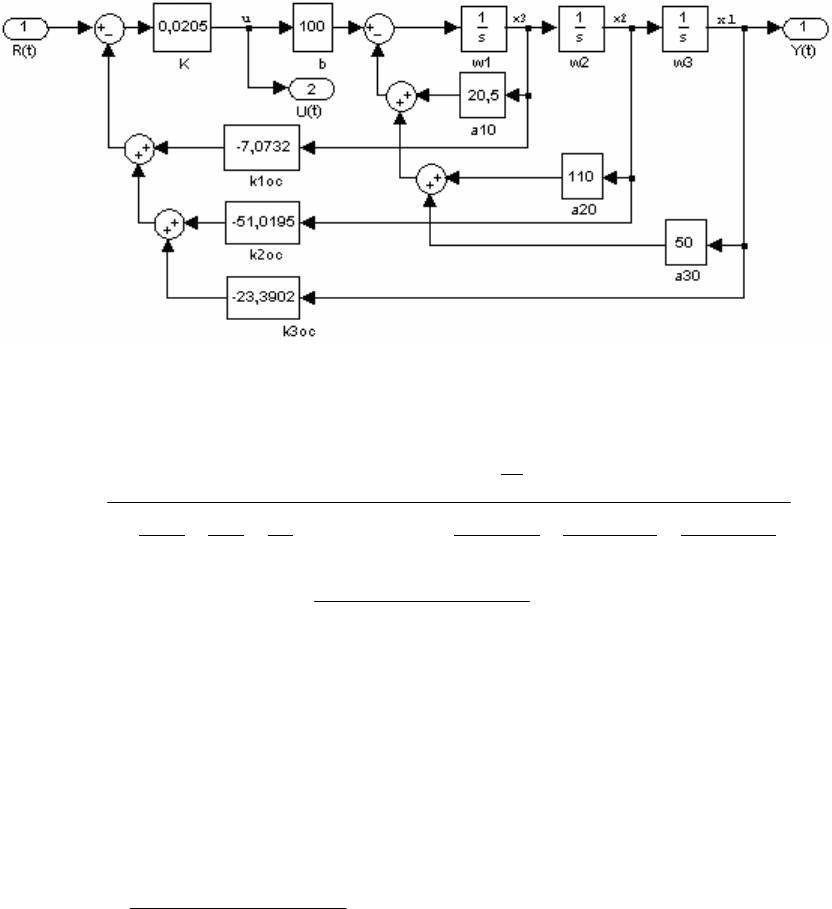
96
Рисунок 1.48
Передаточная функция замкнутой системы регулирования равна
3
2 3 2 3
1
0,0205 100
( )
20,5 110 50 7, 0732 51,0195 23,3902
1 0,0205 100
yr
s
W s
s s s s s s
3 2
2,05
6 5, 41 2,05
s s s
.
Расчет подтверждает, что установившаяся ошибка отсутствует,
так как коэффициент передачи в установившемся режиме равен
2,05/2,05 = 1, а полученный характеристический полином системы ре-
гулирования равен желаемому. При единственной обратной связи по
выходу в ней может быть установлен ПДД-регулятор с аналогичным
регулирующим действием и передаточной функцией
100/)3902,230195,510732,7(
)(
)(
2
3,2,
2
1,
ss
sN
ksksk
sH
ocococ
eq
.
1.7.8 Преобразования подобия
При анализе и синтезе многомерных систем необходимо уметь
переходить от одной формы к другой – поскольку все эти системы по-
добные, такой переход называется преобразованием подобия или ба-
зиса.
Один из путей перехода, приемлемый для одномерной системы
– составить по матрицам A, b, c передаточную функцию системы, а по
ней записать требуемое представление в пространстве состояний.
В общем же случае используют матрицу перехода или преобра-
зования базиса Р размера n×n, тогда новая система уравнений состоя-
ния и наблюдения объекта имеет вид
97
)()()(
)()()(
1
1
ttt
ttt
DuhCPy
PBuhPAPh
откуда следует, что матрицы коэффициентов новой системы равны
A
h
=PAP
-1
, B
h
=PB, C
h
=СP
-1
(матрица D, при ее наличии, не претерпе-
вает изменений, поскольку не связана с вектором состояний). Задава-
ясь произвольной матрицей Р необходимого размера, можно получить
бесконечное множество описаний одной и той же системы в про-
странстве состояний. Однако при любых преобразованиях должны
выполняться два важных условия: исходная и преобразованная систе-
ма должны иметь одинаковые собственные значения (характеристиче-
ские многочлены и их корни); преобразование базиса не меняет пере-
даточную функцию системы.
Приведение к канонической управляемой форме: матрица пре-
образования в этом случае равна отношению матрицы управляемости
новой системы к матрице управляемости исходной, т. е. P = Q
c
Q
-1
. Не-
обходимо найти характеристический полином системы, записать мат-
рицы А
с
и b
с
системы в канонической управляемой форме, вычислить
матрицы управляемости обеих систем и по ним матрицу преобразова-
ния Р, с помощью которой осуществляется переход.
Переход к канонической наблюдаемой форме отличается лишь
тем, что используются матрицы наблюдаемости, причем матрица пре-
образования базиса вычисляется по отношению матрицы наблюдае-
мости исходной системы к матрице наблюдаемости новой P = NN
о
-1
(обе матрицы составляются в виде столбца).
Для перехода к управляемой форме должна быть полностью на-
блюдаема пара (А, b), для перехода к наблюдаемой форме должна
быть полностью наблюдаема пара (A, c).
Обратный переход, т. е. возвращение к исходной системе, на-
пример, после выбора параметров модального регулятора, во всех
случаях осуществляется применением матрицы Р в обратном порядке,
т. е. A = P
-1
A
h
P, B = P
-1
B
h
, C = C
h
P, k = k
h
P, где k
h
– матрица обратных
связей замкнутой системы по переменным состояния.
К диагональной форме A
h
= Λ приводятся системы с некратны-
ми вещественными полюсами, при этом матрицы исходной и преобра-
зованной систем связаны соотношением A = TΛT
-1
и матрица преоб-
разования базиса равна P = T
-1
.
Пример: пусть преобразуемый к канонической управляемой
форме объект третьего порядка описывается системой уравнений
98
011 ;
1
0
0
;
030
100
011
cbA
.
Характеристический полином объекта равен D(s)= s
3
+s
2
+3s+3,
матрица управляемости
301
010
100
Q
.
Используя вычисленный характеристический многочлен, запи-
сываем сопровождающую матрицу А
с
, затем для пары (А
с
, b
c
) найдем
матрицу управляемости Q
с
новой системы и матрицу преобразования
Р=Q
c
Q
-1
133
100
010
c
A ;
211
110
100
c
Q ;
111
011
001
P ;
110
011
001
1
P .
Применяя формулы А
с
=РАР
-1
, b
c
=Pb, c
c
=cP
-1
, найдем описание
системы в канонической форме управляемости (учитывая, что две
матрицы были нам уже известны, оставалось вычислить лишь с
с
)
012 ;
1
0
0
;
133
100
010
ccc
cbA
.
99
2 Начала MATLAB
2.1 Знакомство с программой
Среда MATLAB (матричная лаборатория) – открытая система,
состоящая из основной части и пакетов расширения [2-5], предна-
значенных для решения научных, технических или математических
задач. Система может расширяться и за счет функций пользователя,
реализованных в виде текстовых исходных модулей программ (фай-
лов с расширением .m).
Пакет расширения Control System Toolbox специально разрабо-
тан для исследования систем управления.
Совместно с данным пакетом могут использоваться, дополняя
его, такие пакеты расширения, как Simulink, Fuzzy Logic Toolbox,
Model Predictive Control Toolbox, Robust Control Toolbox, Simulink
Control Design, Simulink Design Optimization, System Identification
Toolbox, Symbolic Math Toolbox. Наиболее важным из них является
Simulink – конструктор структурных схем систем с возможностью мо-
делирования их поведения во времени.
При первом запуске программы количество открытых окон пре-
вышает необходимое (рисунок 2.1).
Рисунок 2.1
100
На начальных этапах работы рекомендуется использовать толь-
ко командное окно (Command Window). Для этого следует выбрать
опцию в меню Desktop-Desktop Layout-Command Window Only. Здесь
же рекомендуется убрать флажок у опции Toolbars-Shortcuts. Вид диа-
логового окна программы упрощается.
Остальные окна можно вызвать позднее: либо по отдельности,
установив флажки (птички) против названий в меню, либо все сразу с
помощью опции Desktop-Desktop Layout-Default (вид по умолчанию).
Возможно использование окон Command History (журнал команд),
Current Directory (текущая папка, по умолчанию это Мои_докумен-
ты\MATLAB или \Work), Workspace (рабочее пространство или база
данных, хранящая все сведения о переменных и объектах текущей
сессии, может быть сохранена и вызвана повторно). Команда clc очи-
щает Command Window, команда clear обнуляет значения переменных
пользователя и восстанавливает значения по умолчанию системных
переменных. Можно очистить командное окно через главное меню
Edit-Clear Command Window или контекстное меню окна.
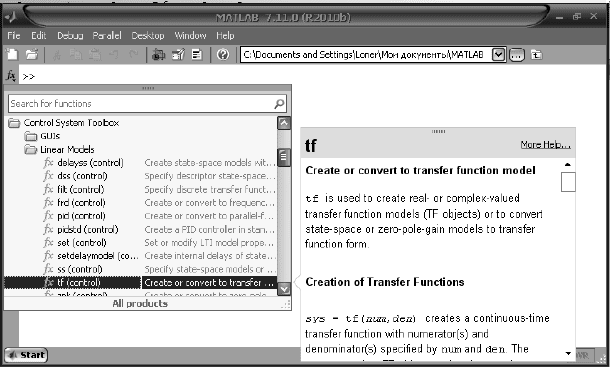
По умолчанию слева от приглашения выводится кнопка f
x
Browse for functions (Shift+F1) каталога функций (рисунок 2.2).
Рисунок 2.2
С ее помощью можно просмотреть весь набор функций, полу-
чить информацию по каждой из них. Вызвав щелчком правой кнопки
мыши на рабочем поле контекстное меню, можно убрать эту кнопку
или восстановить ее вновь Hide/Show Function Browser Button.
Через меню File-Preferences задаются основные характеристики
общения MATLAB с пользователем, например, параметры шрифта,
формат вывода и т. п. (рисунок 2.3). Рекомендуется сразу же в меню
